福岛核事故之后,全厂断电事故缓解措施方面的研究受到广泛的关注。鉴于全厂断电事故可能带来的严重后果,先进的核电技术都设置了相应的安全系统来应对全厂断电事故。CAP1400是先进的第三代核电堆型,安全系统采用了非能动安全设计理念。在全厂断电事故下,反应堆停堆后一段时间内,堆芯衰变热将由蒸汽发生器(Steam Generator, SG)带至二回路,但由于SG二次侧给水的丧失导致二次侧的水位逐渐降低,当出现SG二次侧低水位信号时触发非能动余热排除系统(Passive Residual Heat Removal system, PRHR)。之后,由SG和PRHR共同带出堆芯热量,将堆芯余热降低到低水平,但PRHR这个过程中起着主导作用。因此,在全厂断电事故下,PRHR的换热能力和稳定性是决定反应堆安全的关键因素。
基于PRHR系统的重要性,国内外学者针对PRHR系统开展了大量的研究工作。在试验研究方面:国外主要是西屋公司开展的三管试验[1]、俄勒冈州立大学开展的APEX系列试验[2-3]、意大利的SPES-2系列试验及ROSA/AP600系列试验。国内主要有针对CAP1400非能动堆芯冷却系统而开展的整体性能试验和华北电力大学开展的池式沸腾下的冷凝与沸腾研究[4];在数值计算方面,主要是通过Relap5、FLUENT、CFX等针对AP1000 PRHR系统进行简化建模,计算并进行结果分析,获得了AP1000 IRWST内的流场分布[5-8]。
由调研的文献可知,大多数的数值计算的研究对象是AP1000核电厂的PRHR系统,而针对大型试验装置上的PRHR系统的计算相对较少。本文以CAP1400非能动堆芯冷却系统试验装置上的PRHR系统为研究对象,利用计算流体动力学(Computational Fluid Dynamics, CFD)软件针对PRHR系统进行建模计算,分析了内置换料水箱(In-containment Refueling Water Storage Tank, IRWST)内的流动和传热特性。
1 计算模型及边界条件 1.1 数学模型在单相阶段,以N-S方程为基础,引入了k-ε湍流模型使得N-S方程封闭。
k方程:
| $ \begin{align} &\frac{\partial (\rho k)}{\partial t}+\frac{\partial (\rho k{{u}_{i}})}{\partial {{x}_{i}}}=\frac{\partial }{\partial {{x}_{j}}}[(\mu +\frac{{{u}_{t}}}{{{\sigma }_{k}}})\frac{\partial k}{\partial {{x}_{j}}}]+ \\ &\ \, {{G}_{k}}+{{G}_{b}}-\rho \varepsilon -{{Y}_{M}}+{{S}_{k}} \end{align} $ | (1) |
ε方程:
| $ \begin{align} &\frac{\partial (\rho \varepsilon )}{\partial t}+\frac{\partial (\rho \varepsilon {{u}_{i}})}{\partial {{x}_{i}}}=\frac{\partial }{\partial {{x}_{j}}}[(\mu +\frac{{{u}_{t}}}{{{\sigma }_{\varepsilon }}})\frac{\partial \varepsilon }{\partial {{x}_{j}}}]+ \\ &\ \, {{C}_{1\varepsilon }}\frac{\varepsilon }{k}({{G}_{k}}+{{C}_{3\varepsilon }}{{G}_{b}})-{{C}_{2\varepsilon }}\rho \frac{{{\varepsilon }^{2}}}{k}+{{S}_{\varepsilon }} \end{align} $ | (2) |
式中:
在两相阶段,引入热相变模型,两相间的质量传递模型如下:
连续相通过相界面的总热流量
| $ {{Q}_{\alpha }}={{q}_{\alpha }}-{{\dot{m}}_{\alpha \beta }}{{H}_{\alpha s}} $ | (3) |
离散相通过相界面的总热流量
| $ {{Q}_{\beta }}={{q}_{\beta }}+{{\dot{m}}_{\alpha \beta }}{{H}_{\beta s}} $ | (4) |
根据两相间的热平衡
| $ {{\dot{m}}_{\alpha \beta }}=\frac{{{q}_{\alpha }}+{{q}_{\beta }}}{{{H}_{\alpha s}}-{{H}_{\beta s}}} $ | (5) |
式中:
本文的计算对象是非能动堆芯冷却系统试验装置上的PRHR系统,其IRWST不同于原型核电厂IRWST的形状。试验装置中的IRWST由圆柱形筒体和上、下两个半球形封头构成。本文的计算模型包括IRWST及其内部的C型传热管,考虑到计算机能力的限制,本文建立的几何模型在实际试验装置的基础上进行了简化。具体的简化内容为:1) 将IRWST简化成圆柱形桶体的水箱,不带上、下两个封头;2) 将C型传热管的数量减少成24根,但传热管几何形状和尺寸与实际情况完全一致;3) 假设每根C型传热管的换热能力是相同的,由于C型传热管数量的减少将导致单位时间内向IRWST内传递的热量减少,因此,为了使IRWST内的温升速率接近于实际情况,将IRWST的体积进行相应的减小。考虑到IRWST内存在自然对流的现象,高度是其重要的影响因素,因此通过减小IRWST的直径来减小体积,高度上保持不变。
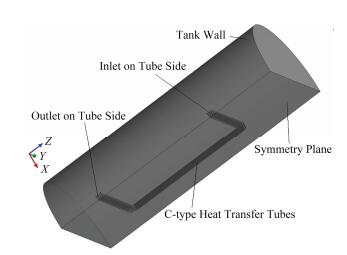
基于以上简化,再考虑到几何模型的对称性,实际计算模型中的传热管数量为12根,沿X轴方向3列,沿Z轴方向4列,成正方形排列,几何模型如图 1所示。为了提高计算精度和效率,几何模型的网格采用六面体网格。为了体现流体的边界层效应,采用Bi-Geometric准则对C型传热管内、外壁面进行局部的网格加密,壁面处第一层网格0.066,第二层网格在第一层的基础上放大1.3倍,后面的依此类推,Y+约为39。网格总数100万,整体网格质量0.35以上。
|
图 1 计算模型的几何示意图 Figure 1 Geometry of the calculate model. |
进行C型传热管内、外耦合的瞬态计算,时间步长0.01s。具体的边界条件为:C型换热器管侧入口流量0.37 kg·s−1,入口温度240℃,出口压力8.5MPa;C型传热管管壁厚度4 mm;水箱初始温度10℃,初始压力0.1 MPa,流体为两相流,水箱顶部、底部、侧壁面绝热。
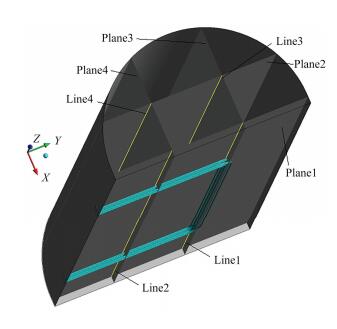
2 计算结果及分析由于计算的几何模型是三维模型,为了便于进行结果分析,选取了4个二维截面和4条直线来分析IRWST内的流动和传热特性,其相对位置示意图如图 2所示。原点位于截面1与水箱壁面的左侧交线上,距C型传热管上、下部水平段的垂直距离相等;截面1是X=0m的YZ平面,位于两列C型传热管的中间位置,靠近管束区;截面2是X=−0.4m的YZ平面,远离管束区域;截面3是Y=1m的XZ平面,位于4列C型传热管竖直段的中间位置,靠近管束区;截面4是Y=0.5m的XZ平面,远离管束区。4条直线分别是4个截面的交线。
|
图 2 截面及直线的相对位置示意图 Figure 2 Relative position diagram of planes and lines. |
在7000s时,IRWST顶部区域温度达到饱和温度,有部分汽相生成。考虑到实际的IRWST是个开口水箱,水箱内的水会因为蒸发而导致水位降低,但本次计算不考虑水箱水位的变化,因此,选择水箱顶部有少量气泡生成的时刻为分析对象。
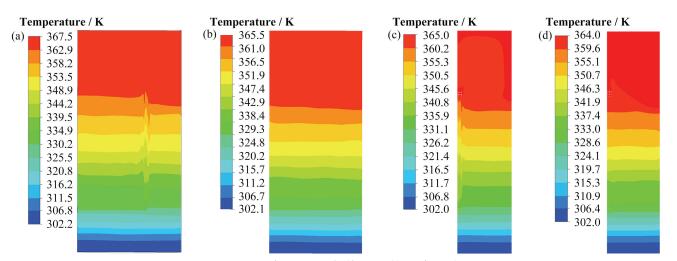
图 3给出了该时刻下水箱内部不同位置的4个纵向截面上的温度分布云图。从4幅云图可以看出,水箱内各个区域沿垂直高度方向上都存在明显的温度分层现象,而温度在水平方向展平,分布得比较均匀,这一规律与其他学者的研究成果一致[5-8]。由图 3(a)可以看出,温度分层现象在靠近C型传热管区域变得更加明显,局部区域呈伞状分布;对比图 3(b)、(d)可以看出,在远离C型传热管区域,流体的温度分布情况是一致的;从图 3(c)可以看出,在靠近C型传热管竖直段区域,流体的温度要略高于远离的区域,且该区域呈现伞状温度分层现象。
|
图 3 4个不同纵向截面上的温度分布云图 (a)截面1,(b)截面2,(c)截面3,(d)截面4 Figure 3 Temperature distribution contour on four different longitudinal planes. (a) Plane1, (b) Plane2, (c) Plane3, (d) Plane4 |
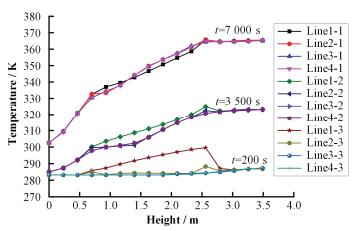
图 4给出了水箱内不同时刻和不同位置处的温度分布曲线。Line1-1-Line4-1分别代表 4条曲线在7000s时刻下的温度分布,Line1-2-Line4-2分别代表 4条曲线在3500s时刻下的温度分布,Line1-2-Line4-2分别代表 4条曲线在200s时刻下的温度分布。
|
图 4 不同时刻和不同位置处的温度分布曲线 Figure 4 Temperature curves at different times and different locations. |
在换热过程的早期阶段(t=200s),Line1靠近传热管竖直段部分的温度要明显高于其它三条直线上的温度,其它三条直线上的温度值均处于水箱的初始温度值。说明在早期阶段,水箱内还未形成自然对流,水箱内主要是通过传热管壁与水之间的热传导来进行热量传递,从而导致靠近C型传热管壁面的位置温度较高,其它区域基本处于初始状态。
在换热过程的中期阶段(t=3500s),Line1靠近传热管竖直段部分的温度要略高于其它三条直线上的温度。其它三条直线几乎是重合的,说明该时刻下温度已经在水平方向上展平,但此时水箱底部的温度还处于初始温度。
在换热过程的后期阶段(t=7000s),在该时刻下,水箱顶部区域已达到饱和状态,水箱底部区域温度也有明显的升高。温度在水平方向上展平,分布得比较均匀。Line1靠近传热管竖直段部分的温度与其它三条直线上的温度之间的规律不明显,可能是在靠近传热竖直段的区域自然对流强烈,扰动较大造成的。
综上所述,在换热进程的早期阶段,水箱内的自然对流尚未建立,此时只有靠近传热管壁区域的温度高,其它区域的温度尚处于初始状态。在换热进程的中后期阶段,水箱内沿垂直高度方向上呈现明显的温度分层现象,温度沿水平方向分布比较均匀。
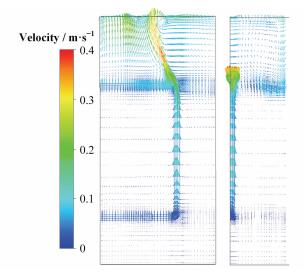
2.2 速度场分析 2.2.1 t=7000s时速度场的分析图 5给出了该时刻下截面1和截面3上的速度矢量图。纵观整个水箱内的速度分布情况,发现水箱内的流动主要集中在C型传热管竖直段附近,沿着竖直段从下向上流动。因此,选取两个通过C型传热管竖直段区域的纵向截面进行分析。
|
图 5 截面1和截面3上的速度矢量图 Figure 5 Velocity vector on Plane1 and Plane3. |
在图 5中,左侧是截面1上的速度矢量图,右侧是截面3上的速度矢量图。从图 5可以看出,在水箱内的中下部区域,流体主要是沿着C型传热管竖直段向上运动,在水箱的上部区域,呈现漩涡状的流动,增强了横向流动。
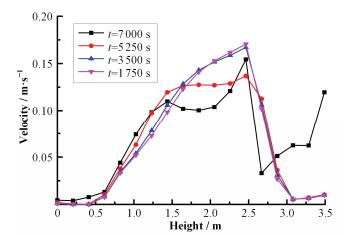
2.2.2 不同时刻下速度变化特性分析Line1靠近C型传热管的竖直段,该区域速度要明显高于其它区域。因此,图 6给出了4个不同时刻下Line1上的速度分布曲线。
|
图 6 4个不同时刻下Line1上的速度分布曲线 Figure 6 Velocity distribution curves on Line1 at different times. |
在1750s和3500s时刻,速度的分布曲线是重合的。在低于传热管下部水平段的区域,速度几乎为0。之后,速度在沿垂直高度方向上逐渐增大,在传热管竖直段的顶端达到最大值。之后,速度沿垂直高度方向逐渐减小。
在5250s时刻,速度沿着垂直高度方向逐渐增大,在传热管竖直段顶部达到最大值。之后,速度沿垂直高度方向逐渐减小,趋势与上述两个时刻是一致的。
在7000s时刻,在Line1中下部区域,速度的变化趋势与上述三时刻是一致的,在上部区域有一定的差异。整体的趋势还是传热管竖直段区域的速度要高,且在竖直段顶部达到最大值。之后,速度先减小再增大。速度减小是由于流体逐渐远离管束区(热源区),速度增大主要由于水箱上部区域有汽相生成,增强了上部的自然对流。
综上所述,在单相自然对流阶段,流体沿C型传热管竖直段向上流动,流动速度逐渐增大,在水箱上部区域速度又逐渐减小。在两相阶段,传热管竖直段区域的流动基本与单相阶段一致,但在水箱的上部区域形成漩涡状流动,增强了该区域的流动,流速明显高于单相阶段上部区域的流速。
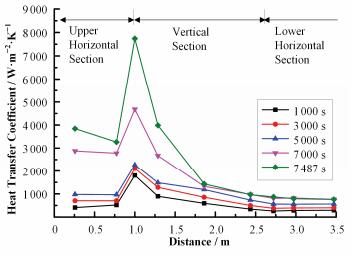
2.3 壁面换热系数分析图 7给出了不同时刻下C型传热管上各段的壁面换热系数的分布曲线。图 7中横坐标轴代表的是距C型传热管入口的距离。从图 7中可以看出,在整个换热进程中,C型传热管上部水平段的换热系数要高于下部水平段,C型传热管竖直段的上部区域的换热系数要高于下部区域的换热系数;在7000s之前,水箱内处于单相自然对流的状态,整体的对流换热系数偏低;在7000s之后,水箱的上部区域达到饱和状态,有部分汽相生成,增强了上部区域的扰动,使得传热管上部水平段和竖直段上部区域的换热系数明显增大;C型管上部水平段和竖直段的连接处的换热系数最大,因为此处的速度是最高的区域。图 7给出的换热系数的分布规律与张钰浩等[4]开展试验研究获得的分布规律一致。
|
图 7 不同时刻下换热系数沿C型传热管的分布曲线 Figure 7 Heat transfer coefficient of C-type tubes at different times. |
通过对非能动堆芯冷却系统试验装置上的PRHR热交换器进行数值计算,得出以下结论:
1) 除了传热的早期阶段之外,在整个换热进程中,水箱内垂直高度方向上呈现明显的温度分层现象,且温度沿水平方向展平,呈现均匀分布的规律。
2) 在单相自然对流阶段,水箱内的流动主要是沿着C型传热管竖直段向上流动,且速度在竖直段的顶端达到最大;在两相阶段,中下部区域的流动与单相阶段一致,上部区域由于有汽相生成,增强了上部的自然对流,使得水箱上部速度增大。
3) 在整个换热进程中,C型传热管上部水平段和竖直段上部区域的壁面换热系数要明显高于其它区域,且在上部水平段与竖直段连接处换热系数最大;在两相阶段,上部区域的壁面换热系数明显增大。
| [1] |
Corletti M M, Hoehreiter L E, Squarer D. AP600 passive residual heat exchanger test[C]. The 1st JSME/ASME Joint International Conference on Nuclear Engineering, Tokyo, Japan, 1991.
|
| [2] |
Reyes J N, Groome G T, Lafi A Y, et al. Final report of NRC AP600 research conducted at Oregon State University (NUREG/CR-6641)[R]. Washington, DC, U.S.:Division of Systems Technology, Office of Nuclear Regulatory Research, U.S. Nuclear Regulatory Commission, 1999.
|
| [3] |
Reyes J N, Hochreiter L. Scaling analysis for the OSU AP600 test facility (APEX)[J]. Nuclear Engineering and Design, 1997, 186(1-2): 53-109. |
| [4] |
张钰浩, 陆道纲, 王忠毅, 等. AP1000非能动余热排出热交换器缩比C型管束二次侧传热模型实验研究[J]. 原子能科学技术, 2016, 50(10): 1763-1770. ZHANG Yuhao, LU Daogang, WANG Zhongyi, et al. Experimental investigation heat transfer model for secondary side of scaled C-shape bundle used in PRHR HX of AP1000[J]. Atomic Energy Science and Technology, 2016, 50(10): 1763-1770. DOI:10.7538/yzk.2016.50.10.1763 |
| [5] |
夏会宁. AP1000核电厂非能动余热排出热交换器数值模拟及其设计优化[D]. 北京: 华北电力大学, 2014. XIA Huining. Numerical simulation and optimized design on passive residual heat removal heat exchanger in AP1000[D]. Beijing:North China Electric Power University, 2014. |
| [6] |
薛若军, 邓程程, 彭敏俊. 非能动余热排出热交换器数值模拟[J]. 原子能科学技术, 2010, 44(4): 429-435. XUE Ruojun, DENG Chengcheng, PENG Minjun. Numerical simulation of passive residual heat removal heat exchanger[J]. Atomic Energy Science and Technology, 2010, 44(4): 429-435. |
| [7] |
张文文, 丛腾龙, 田文喜, 等. 非能动余热排出热交换器换热能力数值分析[J]. 原子能科学技术, 2015, 49(6): 1032-1038. ZHANG Wenwen, CONG Tenglong, TIAN Wenxi, et al. Numerical analysis on heat removal capacity of passive residual heat removal heat exchanger[J]. Atomic Energy Science and Technology, 2015, 49(6): 1032-1038. DOI:10.7538/yzk.2015.49.06.1032 |
| [8] |
宋阳, 李卫华, 李胜强. 非能动余热排出热交换器自然循环数值模拟[J]. 原子能科学技术, 2012, 46(S1): 767-770. SONG Yang, LI Weihua, LI Shengqiang. Natural convection simulation of passive residual heat removal heat exchanger[J]. Atomic Energy Science and Technology, 2012, 46(S1): 767-770. |


