随着核技术应用的迅速发展,我国的放射源数量在近20年来以年均15%的速度增长[1]。然而因为缺乏科学有效的管理,国内的放射源事故平均每年发生30多起[2],部分放射源或放射性材料流失在外界环境中,对社会公众安全和生态环境造成了严重的危害。因此,如何快速寻回遗失的放射源,降低对人和环境的潜在危害显得尤为重要。
传统的放射源搜索方法通过固定式或移动式的射线探测器进行区域搜索,不能直接对放射源进行定位[3],这种方法不但耗时费力而且会使测量人员吸收更多的剂量。传统的γ相机在一定范围内可以对放射源成像,但是它的铅准直系统体积大、笨重、探测效率低[4]。采用准直器与探测器配合共同定位放射源位置的方法[5‒6]与传统方法相比在精度上和效率上有大幅度提高,但它的视野范围较小,需要旋转多次全覆盖,其分辨距离也比较短,仍然需要测量人员在辐射区域滞留较长的时间进行测量。
本文设计的由NaI、CsI、锗酸铋(Bi4Ge3O12, BGO)三晶体耦合的γ射线方向探测器能够直接在辐射区域中快速分辨出放射源射线的入射方向,从而有效地对放射源进行定位,减少了辐射探测人员的受照射时间。
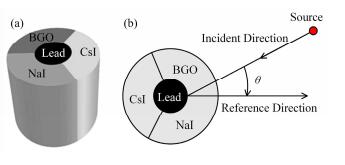
1 探测器模型及放射源定位原理三晶体耦合γ射线方向探测器由圆环柱体的NaI、CsI和BGO晶体及中央圆柱铅芯组成。其模型示意图见图 1,组成探测器的材料参数见表 1。
|
图 1 探测器模型(a)与探测示意图(b) Figure 1 Model of three coupled-crystals directional detector of gamma rays (a) and schematic diagram of detector (b). |
| 表 1 探测器组成材料性能参数 Table 1 Material performance parameters of detector. |
对于三种不同的闪烁晶体而言,探测效率是不同的。因此将这三种晶体耦合起来共用一个光电倍增管,所得脉冲信号通过多道分析器处理之后,各个闪烁体在能谱中的全能峰是分离的[7]。由于采用了三种晶体耦合的圆柱形结构形式,当射线的入射方向不同时,晶体的计数将不同[8],因此根据晶体中计数变化规律就可以得到放射源的方向信息。
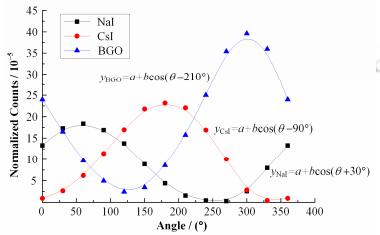
如图 1所示,定义探测器中NaI和BGO晶体交界所在直线的方向为探测器的参考方向,利用基于蒙特卡罗方法的通用软件包MCNP (Monte Carlo N Particle Transport Code)对三晶体耦合探测器的方向分辨情况进行了模拟,结果如图 2所示。
|
图 2 三晶体耦合γ射线方向探测器角度-计数响应曲线 Figure 2 Responding curve of three coupled crystals directional detector of γ rays. |
对图 2中的曲线进行拟合,三条曲线都近似满足:
| $ y=a+b\sin \theta $ | (1) |
式中:y为计数或计数率;a和b为常数,与环境本底、放射源活度及探测器本身相关;θ为放射源与探测器连线相对于参考方向的夹角,如图 1所示。
为了有效消除环境本底的干扰,降低角度测量的不确定性,引入一种较为有效的测量方式——4次测量法[9]。即在同一位置从参考方向开始测量,之后每次将探测器探头旋转90°再进行测量[10],共测量4次,其计数结果分别用yA、yB、yC、yD表示,若放射源和探测器的连线方向与参考方向的夹角为θ,根据式(1),4次测量结果可以由式(2)‒(5) 表示:
| $ {{y}_{\text{A}}}=a+b\cos \theta $ | (2) |
| $ {{y}_{\text{B}}}=a+b\cos (\theta +90{}^\circ ) $ | (3) |
| $ {{y}_{\text{C}}}=a+b\cos (\theta +180{}^\circ ) $ | (4) |
| $ {{y}_{\text{D}}}=a+b\cos (\theta +270{}^\circ ) $ | (5) |
定义反应函数为:
| $ R=({{y}_{\text{A}}}-{{y}_{\text{C}}})/({{y}_{\text{B}}}-{{y}_{\text{D}}}) $ | (6) |
将yA、yB、yC、yD代入反应函数中,则有:
| $ R=\frac{{{y}_{\text{A}}}-{{y}_{\text{C}}}}{{{y}_{\text{B}}}-{{y}_{\text{D}}}}=\frac{\cos \theta -\cos (\theta +180{}^\circ )}{\cos (\theta +90{}^\circ )-\cos (\theta +270{}^\circ )} $ | (7) |
| $ \theta =\text{arccot} (-\frac{{{y}_{\text{A}}}-{{y}_{\text{C}}}}{{{y}_{\text{B}}}-{{y}_{\text{D}}}}) $ | (8) |
式中:R值在0°≤θ≤180°范围内有唯一确定值,且与本底及放射性活度等无关,因此该方法可消除环境本底的干扰,降低测量的不确定度。
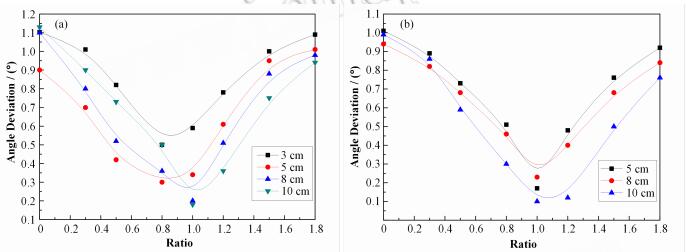
2 探测器角度分辨率影响分析 2.1 铅芯-晶体比例对探测器角度分辨率的影响为了分析引入铅芯对探测器角度分辨率的影响,找到探测器中铅芯与晶体的最佳比例,我们选择高度为10 cm,半径分别为3 cm、5cm、8 cm和10 cm的探测器进行模拟,并不断改变探测器中铅芯的半径来构造不同的铅芯-晶体比例,模拟所用放射源为137Cs和60Co,所得结果如图 3所示。
|
图 3 137Cs (a)和60Co (b)源下的探测器铅芯晶体比例与角度偏差曲线 Figure 3 Angular deviation curve of detector effected by different lead-crystal ratios under source of 137Cs (a) and 60Co (b). |
从图 3可以看出,引入铅芯在一定程度上能够降低探测器的角度偏差,提高角度分辨率。随着铅芯比例的继续增大,探测器的角度偏差开始增大。这是因为加入铅芯之后消除了三种闪烁体之间的部分干扰,所以探测器的角度偏差减小;当铅芯比例继续增加,闪烁体在探测器中所占比例开始减小,探测效率降低,探测器的角度偏差变大。随着探测器尺寸的增加,小比例铅芯不能较好地消除三种晶体的相互干扰,因此图 3中半径为8cm和10cm的探测器在铅芯增加阶段的角度偏差比半径为5cm探测器略大;当铅芯半径增大至过饱和时,此时闪烁体的相互干扰已被降到最低,探测器角度偏差增加主要是因为闪烁体体积减小,由于大体积探测器在铅芯过饱和阶段的闪烁体体积比小体积探测器的要大一些,所以体积较大探测器的角度偏差比较小。
对于137Cs源,3cm和5cm的探测器在铅芯比例为0.8时,角度偏差最小;8cm和10cm的探测器在铅芯比例为1.0时角度偏差最小。对于60Co源,探测器在铅芯比例约为1.0时角度偏差最小。综合考虑137Cs和60Co的模拟结果,如果使探测器的角度分辨率偏差在0.331μGy·h-1处不大于1°,则可选择长为10 cm、半径为5 cm、铅芯-晶体比例为0.8的探测器。
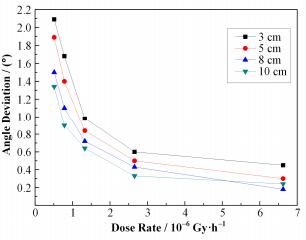
2.2 剂量率对探测器角度分辨率的影响对点源而言,其剂量率和距离的平方成反比关系。为研究放射源剂量率对探测器角度分辨率的影响,我们选择高为10 cm、铅芯-晶体比例为0.8,半径为3 cm、5 cm、8 cm和10 cm的三晶体探测器,所用放射源为137Cs。模拟时保持探测器的位置不变,将放射源放置在距探测器不同距离处的位置以对应不同的剂量率,所得结果如图 4所示。
|
图 4 不同剂量率处的探测器角度偏差曲线 Figure 4 Angular deviation curve of detector measured at positions with different dose rates. |
从图 4可以看出,在一定范围内,随着放射源剂量率的增加,探测器的角度偏差逐渐减小。在高剂量率附近,探测器的角度分辨率较好;在低剂量率处探测器的角度分辨率较差。对不同半径的探测器进行模拟之后的结果表明,在低剂量率位置处,尺寸较大的探测器,其角度分辨率较好,角度偏差较小;尺寸较小的探测器,角度分辨率较差,角度偏差较大。
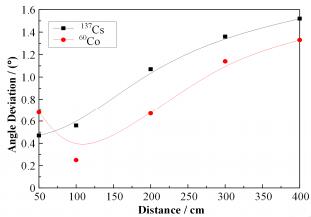
2.3 不同能量射线对探测器角度分辨率的影响为研究不同能量射线对探测器角度分辨率的影响,我们选择长度为10 cm、半径为5 cm、铅芯与晶体比例为0.8的探测器,射线源为137Cs与60Co,将放射源置于距探测器不同距离处依次进行模拟,所得结果如图 5所示。
|
图 5 137Cs与60Co的探测器角度偏差曲线 Figure 5 Angular deviation curve of 137Csand 60Co. |
从图 5可以看出,在靠近放射源位置处时,探测器对137Cs源的角度偏差略小于60Co的角度偏差,这是因为60Co射线的能量比137Cs高,在近距离处的穿透能力比较强,在闪烁体中沉积的光子数较少,因此角度偏差比137Cs稍大一点;随着距离的增加,源剂量率开始降低,由于60Co的能量较高,在相同位置处60Co源的空气吸收剂量率比137Cs源的空气吸收剂量率高,因此探测器在远距离处对60Co射线的角度偏差较137Cs射线小一些。
3 空间放射源模拟定位有时候放射源所处的位置具有一定的高度,因此需要对存在于空间中的放射源进行定位。模拟定位空间放射源所用的探测器长为10 cm、半径为10cm、铅芯比例为0.8。探测器A、B垂直于水平面放置,A的坐标(cm)为(0, 0, 0),B的坐标为(0, -100, 0),模拟放射源137Cs坐标为S (500, -500, 400) 其在水平面的投影为S′。设X轴的正半轴方向为参考方向,S′和探测器A、B的连线与参考方向的夹角为θ1、θ2。
为了使空间定位结果更准确,将探测器C平行于XY面放置,且它的坐标与放射源在水平面的投影位置S′有关,S′的位置可由探测器A、B测量得到。探测器C的0°方向与Z轴重合,放射源与探测器的连线SC与S′C的夹角为θ3。模拟定位使用4次测量法,依次逆时针旋转探测器并记录探测器各晶体的全能峰计数,所得结果如表 3所示。
| 表 3 三晶体γ耦合方向探测器模拟定位结果 Table 3 Simulation results of three coupled-crystals directional detectors of gamma rays (°). |
探测器A、B、C均可得出放射源位置的一个角度,且A、B的坐标已知,放射源的坐标S可由式(9)‒(11) 得出。
| $ y/x=-\tan {{\theta }_{1}} $ | (9) |
| $ (y+100)/x=-\tan {{\theta }_{2}} $ | (10) |
| $ z/x=\tan {{\theta }_{3}} $ | (11) |
联立上述三个方程便可计算出放射源的空间位置,用三晶体耦合γ射线方向探测器模拟定位137Cs放射源的空间位置为(471.150, -467.203, 396.759) 与真实位置的相对偏差约为5%。
4 结语本文基于三晶体耦合γ射线方向探测器,讨论了探测器的参数及其他因素对放射源定位精度的影响,所得结论如下:
1) 设计的三晶体耦合γ射线方向探测器能够分辨异常辐射区域内射线的入射方向,对于放射源在各个角度的角度分辨能力较稳定。对137Cs源在空气吸收剂量率≥0.331 μGy·h-1处,其定位角度偏差不超过0.99°;随着辐射场强度的继续降低,放射源定位的角度不确定性将增加。
2) 在一定范围内,适当调整探测器中铅芯-晶体的比例有助于探测器角度分辨率的提高,当探测器的铅芯比约为1.0时,探测器的角度偏差较小;在放射源剂量率较低处,探测器的角度分辨能力较弱;在放射源剂量率较高处,探测器的角度分辨能力较好。
3) 在空气吸收剂量率比较低的位置,尺寸较大的探测器的角度分辨率在一定程度上优于小尺寸的探测器;在进行放射源定位时,使用尺寸较大的探测器所得结果较好,对7 m远、4 m高的137Cs放射源定位的相对偏差约为5%。
| [1] |
周启甫. 我国辐射安全与保安现状及对策[C]. 2007年核技术工业应用分会学术年会, 湖北, 2007: 2-9. ZHOU Qifu. The situation and countermeasure of radiation safety and security in China[C]. The Council Collected Papers of Nuclear Technology and Industry Application in 2007 Annual Conference, Hubei, 2007:2-9. |
| [2] |
范深根. 我国放射事故概况与原因分析[J]. 辐射防护, 2002, 22(5): 277-281. FAN Shengen. General situation of radiation accidents in China and analysis of their causes[J]. Radiation Protection, 2002, 22(5): 227-281. DOI:10.3321/j.issn:1000-8187.2002.05.005 |
| [3] |
Willis M J, Skutnik S E, Hall H L. Detection and positioning of radioactive sources using a four-detector response algorithm[J]. Nuclear Instruments & Methods in Physics Research A, 2014, 767(11): 445-452. DOI:10.1016/j.nima.2014.08.033 |
| [4] |
Powsner R A, Powsner E R. Essential nuclear medicine physics[M]. 2nd ed. UK: Blackwell Publishing, 2008.
|
| [5] |
谭军文, 左国平, 周剑良, 等. NaI探测器搜寻γ源定位准直器模拟设计[J]. 核电子学与探测技术, 2015, 35(4): 354-360. TAN Junwen, ZUO Guoping, ZHOU Jianliang, et al. The simulation design of a positioning collimator to locate the gamma radiation source with NaI detector[J]. Nuclear Electronics & Detection Technology, 2015, 35(4): 354-360. DOI:10.3969/j.issn.0258-0934.2015.04.010 |
| [6] |
Gamage K A A, Joyce M J, Taylor G C. Investigation of three-dimensional localization of radioactive sources using a fast organic liquid scintillator detector[J]. Nuclear Instruments & Methods in Physics Research A, 2013, 707(7): 123-126. DOI:10.1016/j.nima.2012.12.119 |
| [7] |
Shirakawa Y. Development of a direction finding gamma-ray detector[J]. Nuclear Instruments & Methods in Physics Research A, 2007, 263(1): 58-62. DOI:10.1016/j.nimb.2007.04.056 |
| [8] |
Randall G L, Iglesis E, Wong H F, et al. A method of providing directionality for ionising radiation detectors-RadICAL[J]. Journal of Instrumentation, 2014, 9(10): p10011. DOI:10.1088/1748-0221/9/10/p10011 |
| [9] |
左国平, 谭军文, 周剑良, 等. 基于三角圆筒铅屏蔽NaI探测器的放射源定位研究[J]. 原子能科学技术, 2017, 51(3): 515-521. ZUO Guoping, TAN Junwen, ZHOU Jianliang, et al. Study of radioactive source localization based on triangular cylindrical lead shield NaI detector[J]. Atomic Energy Science and Technology, 2017, 51(3): 515-521. DOI:10.7538/yzk.2017.51.03.0515 |
| [10] |
Fujimoto K. A simple gamma ray direction finder[J]. Health Physics, 2006, 91(1): 29-35. DOI:10.1097/01.HP.0000196113.49929.be |


