束流位置探测器(Beam Position Monitor, BPM)是各种不同加速器(包括直线、回旋、同步加速器)中使用最频繁的束流测量元件,它能在不影响束流的情况下(忽略尾场的影响)测量出束团质心横向位置和纵向分布[1-3]。它由与地隔绝的金属电极组成,通过测量束流经过时,在电极上产生感应电荷来得到束团的位置。有时该装置也用于测量束团的纵向长度,称为“电磁拾取电极(Electromagnetic pick-up)”更加准确。
常见的BPM有纽扣型、条带型、斜切型和腔式型等,在北京正负电子对撞机二期(Beijing Electron Positron Collider II, BEPCII)的直线加速器上有20套BPM,其中2套为纽扣型、18套为条带型;而在储存环上有138套纽扣型BPM,其中88套安装在前室结构管道上、42套安装在跑道型管道上、其他的安装在一些特殊位置[4],用于横向束流反馈系统[5]、工作点测量系统、束团流强检测系统[6]、丢束诊断系统[7]等。单次通过的地方,如直线段和传输线,BPM主要用于测量束流的位置以及利用电极和信号反应的流强测传输效率。储存环上的BPM主要用于测量束流的闭轨和逐圈位置[8],能在逐圈、快轨道10 kHz和慢轨道10 Hz等多个模式下提供充足的物理信息。正因为束流位置探测器能提供多维的束流信息,国内外实验室一直在进行相关的研究,比如合肥光源正在进行自由电子激光的纽扣型[9]和条带型[10-11]BPM的研究,上海光源也在进行适用于自由电极激光的、位置分辨率较高的腔式[12-13]BPM研究。
本文主要分析探头产生信号以及在探头中传播的过程。目前BEPCII所用的电子学器件主要是Bergoz和I-tech的商业产品,关于电子学处理方法和相关电子学的介绍可参考文献[14-15],文献[16]中也有关于BPM探头设计的描述,其中部分结果是用MAFIA程序计算得到,本文主要使用的是CST (Computer Simulation Technology)的微波工作室和粒子工作室。
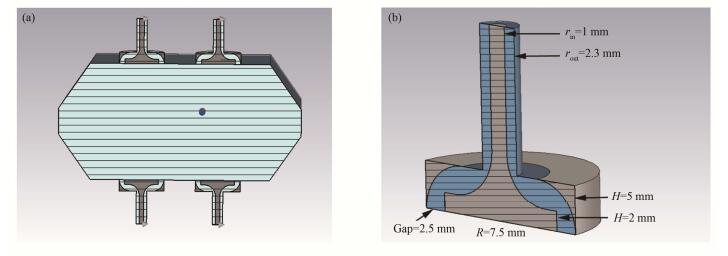
1 CST机械参数与转移阻抗BEPCII储存环大部分真空管道为前室型,部分地方为八边形,极少数地方为圆形(直径为100 mm左右),以八边形为例,水平与垂直方向最大孔径为108 mm×52 mm,其结构如图 1(a)所示,前室型管道与八边形管道相比,在左边多出来一段扁平的管道,计算结果显示两者差别不大。采用的电极为直径为15 mm纽扣型电极,其建模尺寸如图 1(b)所示,其中为保证传输线的特征阻抗为50Ω,建模时的内外导体半径比设计为2.3,填充材料为真空。
|
图 1 BEPCII纽扣型BPM结构 (a)八边形束流管道,(b)纽扣型电极机械尺寸 Figure 1 Mechanical structure of the button BPMs which are widely used in BEPCII. (a) Octagon beam pipe, (b) Mechanical size of button structure |
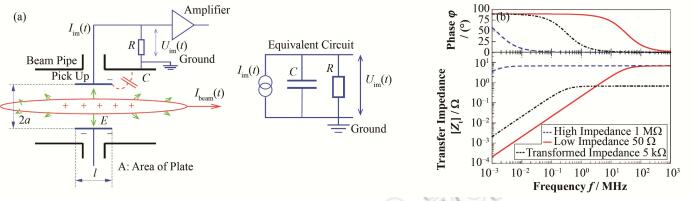
如图 2(a)所示,电容性拾取电极由真空管道内的不同形状的金属电极组成,产生的感应电荷通过穿墙子以及匹配电路耦合出来,经过电子学处理得到束流位置。假设拾取电极与管道中心距离为a,面积为A,纵向长度为l,则镜像电荷Qim驱动产生的镜像电流Iim为:
| $ {{I}_{\text{im}}}(t)=\frac{\text{d}{{Q}_{\text{im}}}}{\text{d}t}=-\frac{A}{2\pi al}\times \frac{\text{d}{{Q}_{\text{beam}}}(t)}{\text{d}t} $ | (1) |
|
图 2 BPM工作原理示意图(a)拾取电极示意图以及其等效电路图,(b)转移阻抗的高通特性、电极的转移阻抗与相位图 Figure 2 Schematic of signal extraction of BPM. (a) The principle diagram of pickups and its equivalent circuit, (b) Absolute value and phase of transfer impedance. |
式中:
对于运动速度为βc的束流有:
| $ \frac{\text{d}{{Q}_{\text{beam}}}(t)}{\text{d}t}=\frac{l}{\beta c}\cdot \frac{\text{d}{{I}_{\text{beam}}}}{\text{d}t}=-\frac{l}{\beta c}\cdot i\omega {{I}_{\text{beam}}}(\omega ) $ | (2) |
式中:Ibeam(ω)=I0∙e-iωt为束流在频域表达式。时域函数(t为变量)到频域(ω为变量)函数的转换可由傅里叶变换完成,电阻R上的电压为:
| $ {{U}_{\text{im}}}(\omega )=R\cdot {{I}_{\text{im}}}(\omega )={{Z}_{t}}(\omega, \beta )\cdot {{I}_{\text{beam}}}(\omega ) $ | (3) |
用来描述BPM的参数较多,比如纽扣尺寸的大小、灵敏度和分辨率等,其中一个最重要的参数为转移阻抗Z(分为横向和纵向,这里主要讨论纵向转移阻抗),它被用来描述BPM对束流的响应。Zt(ω, β)是根据欧姆定律定义的频域下的阻抗,是表征BPM最基本的参数,它描述了电极上电压信号的幅度与束流流强的关系,与频率、粒子速度β和电极的几何形状有关,纵向转移阻抗越大表示在相同的束流强度下信号幅度越大。
如图 2(a)所示,电容性电极通常有一定的对地电容C,它由电极与管道之间的距离以及电极与放大器输入之间电缆的电容决定。放大器的输入阻抗为R,束流可看作电流源,与耦合电容、输入电阻并联,其等效电路如图 2(a)所示,它们之间满足:
| $ \frac{1}{Z} = \frac{1}{R} + i\omega C \Leftrightarrow Z = \frac{R}{{1 + i\omega RC}} $ | (4) |
将式(1)、(4) 代入式(3) 可得:
| $ \begin{array}{*{35}{l}} {{U}_{\text{im}}}=\frac{R}{1+i\omega RC}\cdot {{I}_{\text{im}}}=\frac{1}{\beta c}\cdot \frac{1}{C}\cdot \frac{A}{2\pi a}\cdot \frac{i\omega RC}{1+i\omega RC}\cdot {{I}_{\text{beam}}} \\ \ \ \ \ \ \ ={{Z}_{\text{t}}}(\omega ,\beta )\cdot {{I}_{\text{beam}}}(\omega ) \\ \end{array} $ | (5) |
式(5) 描述了转移阻抗的一阶高通特性,其fcut=ωcut/2π=(2πRC)-1。图 2(b)分别给出了放大器输入阻抗为50Ω、5 kΩ、1 MΩ时转移阻抗的绝对值和相位随频率的变化情况,其中C=100 pF,l=10 cm,β=50%。从转移阻抗的绝对值曲线中可以看到明显的高通特性,在低频区其阻抗值较小,信号较弱。虚、实线显示了高阻和低阻的差异。其中电子机器大多为50Ω阻抗。图 2(b)中转移阻抗的绝对值和相位解析表达式分别为:
| $ \begin{array}{l} \left| {{Z_{\rm{t}}}} \right| = \frac{1}{{\beta c}} \cdot \frac{1}{C} \cdot \frac{A}{{2\pi a}} \cdot \frac{{\omega /{\omega _{{\rm{cut}}}}}}{{\sqrt {1 + {\omega ^2}/\omega _{{\rm{cut}}}^2} }}{\rm{ }}\\ {\rm{ }}\varphi = \arctan ({\omega _{{\rm{cut}}}}/\omega ) \end{array} $ | (6) |
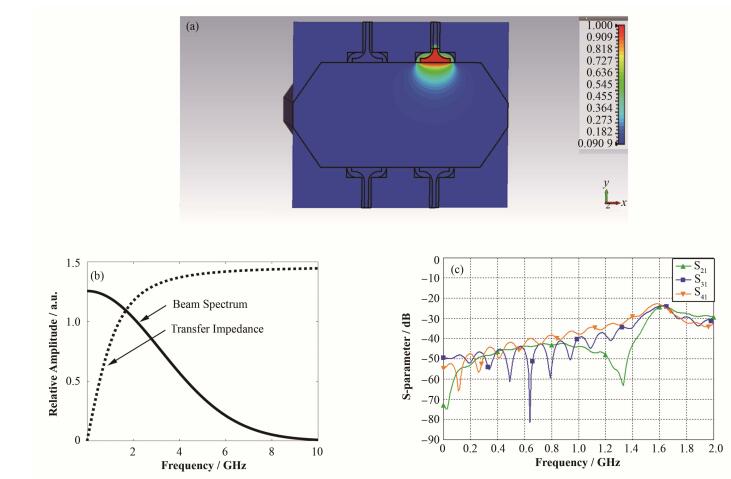
束流的频谱由束团长度决定,时域为高斯分布的束流经过傅里叶变换,在频域分布Ĩbeam(ω)同样是高斯分布,其中心在f=0处,宽度σf=1/(2πσt),其中σt为时域宽度,图 3(b)中实线为束流频谱。对BEPCII而言,标准差σf=1/(2πσt)=3.18 GHz。虚线为转移阻抗大小随频率变化,描述了BPM的高通特性。如果束流频谱远大于fcut,则Ĩbeam(ω)与转移阻抗Zt(ω)相乘后,Ũim(ω)与束流Ĩbeam(ω)形状相同,反傅氏变换得到的时域信号则与束流流强信号随时间变化的曲线相同,称之为正比型信号,电极上的电压信号和束流的流强信号一样是一个单峰。对于束流频谱远小于fcut的情况,Ĩbeam(ω)与转移阻抗Zt(ω)相乘后,Ũim(ω)形状发生了较大的变化。反傅氏变换得到的时域信号Uim(t)∝dI/dt,故此称为导数型信号,得到的电压信号是一正一负的双峰,中间过零点为高斯分布的中心。第三种情况则是介于这两者之间,比如BEPCII上纽扣型BPM就是这种情况。其信号频谱和fcut在同一个量级。计算转移阻抗需要先计算BPM电极的电容。当在其中一个电极上加上一定电压时,其电势分布如图 3(a)所示,从中可知纽扣型的BPM电极之间的耦合较小,图 3(c)显示了一个电极到其它三个电极间的S参数计算结果,在1 GHz以下的频域内,另外三个端口S21、S31、S41均在-50 dB以下。在某一个电极上施加1V电压,根据其所带电荷Q=CU可得到电容C,计算得到的电容值为C=2.14 pF。则fcut=ωcut/2π= (2πRC)-1=1.49 GHz,计算得到转移阻抗最大值Z=1.46 W。具体的转移阻抗随频率如图 3(b)虚线所示。假设束流峰值流强为1 A,电极上得到的峰值电压为U=IR=1.46 V。
|
图 3 转移阻抗的计算(a)等电势线分布,(b)束流频谱与转移阻抗,(c)电极间的耦合 Figure 3 Evaluation of transfer impedance. (a) Isopotential line distribution, (b) Beam loss intensity distribution of synchrotron mode, (c) S-parameters between different electrodes |
在水平和垂直方向分别放置4个独立的BPM电极,根据电极间的信号差异就能得到束流的位置。当束流离电极越近产生的信号越强,这个叫做“近邻效应(Proximity effect)”,水平位置x和垂直位置y可分别表示为:
| $ x = \frac{1}{{{S_x}}} \cdot \frac{{{U_{{\rm{right}}}} - {U_{{\rm{left}}}}}}{{{U_{{\rm{right}}}} + {U_{{\rm{left}}}}}} + {\delta _x} \equiv \frac{1}{{{S_x}}} \cdot \frac{{\Delta {U_x}}}{{\Sigma {U_x}}} + {\delta _x} $ | (7) |
| $ y = \frac{1}{{{S_y}}} \cdot \frac{{{U_{{\rm{up}}}} - {U_{{\rm{down}}}}}}{{{U_{{\rm{up}}}} + {U_{{\rm{down}}}}}} + {\delta _y} \equiv \frac{1}{{{S_y}}} \cdot \frac{{\Delta {U_y}}}{{\Sigma {U_y}}} + {\delta _y} $ | (8) |
电极感应电压信号的差和比(电压差除以电压和)与束流位置之间的比例系数Sx、Sy叫做位置灵敏度,单位是%∙mm-1,反映的是设计的BPM对束流位置变化的灵敏度。通常灵敏度与束流位置有关,在偏移量较大、远离管道中心时,信号的非线性效应会变得明显,此时灵敏度会下降,实际工程中最后得到灵敏度还与信号处理的频率以及电子学信号处理的方法等有关。此处计算的灵敏度是管道中心处、信号处理中心频率为500 MHz时的灵敏度,就是用电极信号的频谱上在500 MHz处的分量进行式(7) 和(8) 的计算。
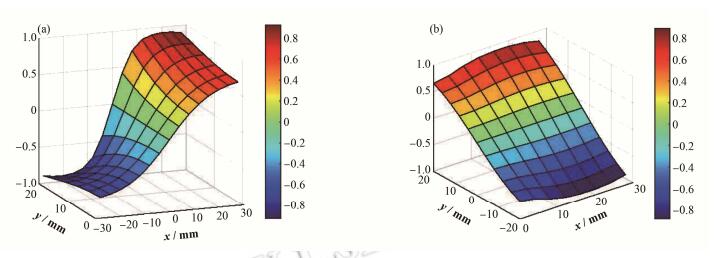
在不同的纽扣间距下,对应的灵敏度如表 1所示,其中第一组值来自于文献[16],第二组值来自于用CST计算。调整两个电极在水平方向的距离可以改变两个方向的灵敏度,当增大两电极的水平距离ΔL时,Sx增大,Sy减小,这样就可以保证两个方向灵敏度相等。从表 1可知,当两电极之间的距离在31-33 mm之间时,两个方向灵敏度大致相等。图 4是和差比信号随束流位置改变的情况,扫描的范围为28 mm×20 mm,从图 4(a)可知,当Y=0、X在-28-28 mm之间变化时,X方向和差比信号线性区较大,灵敏度较小,当Y=20、X在-28-28 mm之间变化时,X方向的线性度区较小,灵敏度较大。从图 4(b)可知,当X=0、Y在-20-20 mm之间变化时,和差比信号几乎都是线性的,而随着X的增大,Y方向的灵敏度先增大后减小,灵敏度最大的地方在X=17 mm附近。中心区的水平和垂直方向的灵敏度分别为Sx=[4.34 %∙mm-1]和Sy=[4.08 %∙mm-1]。水平垂直两个方向的线性区一般为管道与电极距离的1/3左右。
| 表 1 不同的电极结构(电极间水平距离)下的灵敏度 Table 1 Sensitivity of different distance between two buttons. |
|
图 4 位置扫描时和差比随束流位置的变化(a) x方向,(b) y方向 Figure 4 Change of ratio of sum and difference signal with different beam position. (a) Horizontal position, (b) Vertical position |
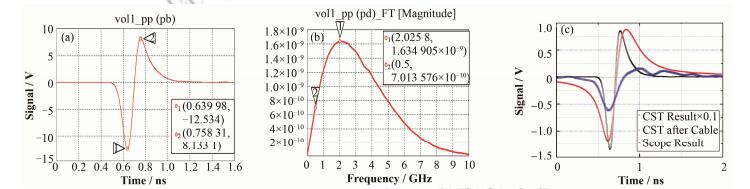
在束团电荷量为1 nC时,CST计算的电压信号的时域与频域结果如图 5所示,其中时域信号介于正比型与导数型信号之间,两个峰之间的时间间隔为∆t=0.118 ns,如果电极上的信号是导数型,则应该在±σt处有极大值和极小值,峰峰值之间间隔应该为2σt=0.1 ns。频谱信号的最大分量位于2 GHz附近,这是由束流频谱与BPM电极转移阻抗性质决定,即图 3(b)中虚、实线相乘的结果,大致在两线交点附近。图 5(c)显示了CST计算的BPM信号经过50 m的LMR-400线缆衰减前后的情况,为便于比较,将经过衰减前的信号幅度乘以0.1,十字交叉线是束测本地站示波器的测量结果,目前计算结果约为实测结果的两倍,可能是CST的BPM模型与实际情况的差别引起的,也可能是线缆的衰减系数经过辐射后引起的变化,目前正准备在下个检修期对线缆进行重新标定。
|
图 5 电荷量为1 nC、束团长度为50 ps时BPM信号(a)时域信号,(b)频域信号,(c)信号实测值与CST计算比较 Figure 5 CST simulation results of the BPM signal. (a) Signal in time domain, (b) Signal in frequency domain, (c) Signals comparing between simulation and measurement |
为了更好地了解束流位置与电极和差比信号之间的关系,需要对BPM做校准,得到所谓的Mapping图,在式(7) 和(8) 中,假设两者是线性关系,更加精确的做法是利用多项式拟合的办法。假设水平和垂直方向的和差比分别为U和V,x、y与U、V之间的拟合关系可用矩阵表达:
| $ x = {\rm{ }}\left[A \right] \cdot \left[{F\left( {U, V} \right)} \right] $ | (9) |
| $ y = {\rm{ }}\left[B \right] \cdot \left[{F\left( {U, V} \right)} \right] $ | (10) |
式中:A、B是由多项式系数构成的行向量;F(U, V)为由对应的各阶多项式构成的列向量。可见,只要在所要求的计算精度下,求出多项式系数行向量,即可以得到BPM的灵敏度。通常可以使用最小二乘法计算式(9) 和(10) 中的多项式系数行向量[11]。
令S为进行多项式拟合时的拟合方差,有:
| $ \begin{align} &S=\sum{{{\left( {{x}_{0i}}-{{x}_{i}} \right)}^{2}}}+\sum{{{\left( {{y}_{0i}}-{{y}_{i}} \right)}^{2}}} \\ &\frac{\partial S}{\partial {{a}_{j}}}=0\ \ \ \frac{\partial S}{\partial {{b}_{j}}}=0 \\ \end{align} $ | (11) |
式中:i表示对所有数据点求和;aj、bj分别为其中的第j个元素;fj(U, V)为其中的第j个元素。当多项式系数aj或bj均满足式(11) 时,多项式拟合方差最小,相应的式(11) 的解即为相应的多项式拟合系数,即多项式系数aj或bj均满足方程:
| $ \frac{{\partial S}}{{\partial {a_j}}} = - 2\sum ({x_{0i}} - {x_i}) \cdot \frac{{\partial {x_i}}}{{\partial {a_j}}} = 0 $ | (12) |
代入式(9) 和(10) 得到:
| $ \begin{array}{l} [A] \cdot \sum\limits_i {([F({U_i}, {V_i})}] \cdot {f_j}({U_i}, {V_i})) = \sum\limits_i ( {x_{0i}} \cdot {f_j}({U_i}, {V_i}))\\ [B] \cdot \sum\limits_i {([F({U_i}, {V_i})}] \cdot {f_j}({U_i}, {V_i})) = \sum\limits_i ( {y_{0i}} \cdot {f_j}({U_i}, {V_i})) \end{array} $ | (13) |
对所有的多项式系数分别求导后,令方程组左边求和符号后的列向量分别为方阵C、D中的列向量Cj、Dj;令方程右边求和符号后的值为行向量E、F中相应的元素Ej、Fj。则各系数方程联立可得:
| $ \begin{array}{l} [A] \cdot [{C_j}] = [E]\\ [B] \cdot [{D_j}] = [F] \end{array} $ | (14) |
此时,不难求得多项式系数A、B。用此多项式系数对模拟计算得到的归一化束流位置信息U、V进行拟合,再与理想束流位置x0、y0对比,可以得到相应阶数的多项式拟合精度。不断调整拟合阶数,即可达到所需拟合精度。
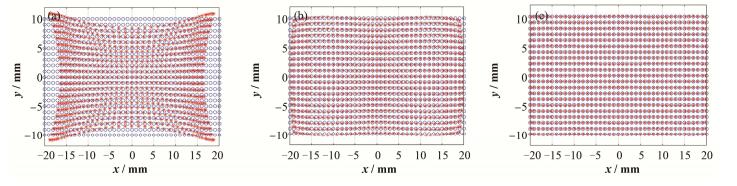
用CST对20 mm×10 mm的区域进行步长为1mm的扫描,计算时的网格数为2.1×105,总时间为6 h左右,得到的UV通过不同阶数多项式拟合图 6所示,圆圈为束流实际位置,星号为拟合结果:从左到右分别为一阶、三阶、五阶拟合得到的水平和垂直位置,从中可知,越高阶的拟合在远离中心的非线性区符合得越好,而一阶近似仅在束流管道中心处符合较好。
|
图 6 不同阶数拟合UV得到的束流位置(a)一阶,(b)三阶,(c)五阶 Figure 6 Sensitivity mapping of BPM at 500 MHz. (a) The first order fitting, (b) The third-order fitting, (c) The fifth-order fitting |
BPM探头上信号的计算分为以下几步:将流强的时域表达式Ibeam(t)进行傅氏变换得到Ĩbeam(ω)。根据转移阻抗得到电压信号的频域表达式Ũim(ω)=Zt(ω)∙Ĩbeam(ω)。最后对Ũim(ω)进行反傅氏变换得到电压信号在时域表达式Uim(t)。BPM的设计与优化主要分为两个部分:一是对机械尺寸的优化即转移阻抗Zt(ω)的优化;二是对信号传输线上的特征阻抗优化。关于转移阻抗的优化,由式(6) 可知,当电极与束流管道中心的距离a变小时,即电极与束流距离越近,转移阻抗越大,信号越强。增大纽扣型电极的面积A也可以增大信号,而增大电极与管道之间的gap会减小电极的电容,从而增大转移阻抗增大信号。第二部分是对信号传输路径上特征阻抗的优化,式(6) 并未考虑信号在传播路径上的传输问题,这一点对条带型BPM尤为重要。与纽扣型BPM相连的一般为穿墙子和同轴线缆,设计时通过陶瓷绝缘材料和机械尺寸的调配,保证其特征阻抗在50Ω左右。有时需要优化的是从纽扣型电极的端面到穿墙子之间这一段距离的结构,减少阻抗的跳变而设计平滑的过渡则有利于减小信号的反射。通常用电压反射系数Г来衡量阻抗匹配。
| $ Z = \frac{{1 +\mathit{\Gamma } }}{{1 -\mathit{\Gamma } }}{Z_0} $ | (15) |
式中:Z0是特征阻抗50Ω,将BPM电极看作是同轴传输线,Z~
| $ {{Z}_{0}}=\frac{120\text{ }\pi\text{ }}{\frac{w}{b}+\frac{2\text{ }\pi\text{ }h}{2a-h}}\ln \frac{a}{a-h} $ | (16) |
为了保证信号在从起始端传到末端再反射回来的过程中不发生信号的畸变,通常会保证都是50Ω的匹配,而在末端一般是短路,条形电极的信号与纽扣型电极的区别在于会有一正一负两个脉冲,而两个脉冲之间的时间间隔则为信号在条形电极上一个来回所需时间,即2l/c。其上游输出端口1的信号可以表示为:
| $ {{U}_{1}}(t)=\frac{1}{2}\cdot \frac{\alpha }{2\text{ }\pi\text{ }}\cdot {{R}_{0}}\cdot \left[{{I}_{\text{beam}}}(t)-{{I}_{\text{beam}}}(t-2l/c) \right] $ | (17) |
代入高斯分布束流的Ibeam(t)=I0∙exp(-t2/2σt2),则有:
| $ {{U}_{1}}(t)=\frac{{{Z}_{\text{strip}}}}{2}\cdot \frac{\alpha }{2\text{ }\pi\text{ }}\cdot \left[{{\text{e}}^{-{{t}^{2}}/2\sigma _{\text{t}}^{2}}}-{{\text{e}}^{-{{(t-2l/c)}^{2}}/2\sigma _{\text{t}}^{2}}} \right]\cdot {{I}_{0}} $ | (18) |
通过傅氏变换条形电极的转移阻抗Zt为:
| $ {{Z}_{\text{t}}}(\omega )={{Z}_\text{strip}}\cdot \frac{\alpha }{4\text{ }\pi\text{ }}\cdot {{\text{e}}^{-{{\omega }^{2}}\sigma _{\text{t}}^{2}/2}}\sin (\omega l/c)\cdot {{\text{e}}^{i(\pi /2-\omega l/c)}} $ | (19) |
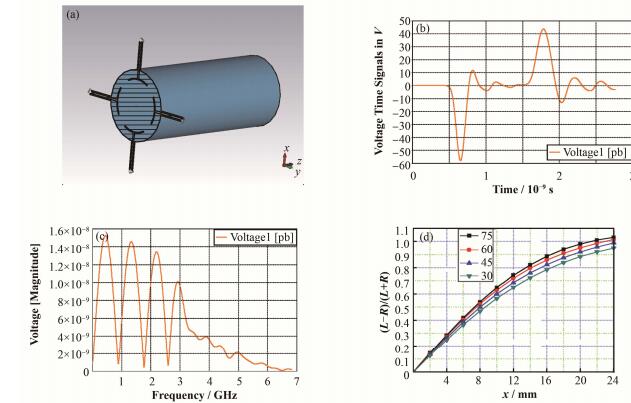
所以条形电极的转移阻抗有一系列最大值,位于fmax=(c/4l)∙(2n-1) 处,其中n=1, 2, 3, ……,对于给定的频率,条形电极的长度l的选择应尽量使其具有更大的转移阻抗,第一个最大值l=c/(4facc)=λ/4,所以有时也称条带型BPM为1/4波长耦合器。500MHz对应的波长为600 mm,所以BEPCII的条形电极的长度为150 mm,具体的机械参数为:管道内径37 mm,电极外径28.2 mm,电极厚1 mm,电极张角60°。根据式(16) 计算所得的特征阻抗为53.1Ω,CST计算结果为56.8Ω。条形电极的信号频谱与CST建模的模型如图 7所示,正负脉冲的信号相差1 ns左右,而频谱上第一个峰值刚好位于500 MHz附近,而相较于纽扣型BPM来说,其频谱和信号也更为复杂。条形电极的设计不光需要考虑特征阻抗、检测频率处分量等,还需要考虑灵敏度与电极之间耦合的问题,增大电极张角可以提高灵敏度,但会引起相邻电极的耦合,但是根据CST的计算,其耦合比预计中小,因为水平和垂直方向是独立的计算位置,在较大电极张角下,电极对相邻电极耦合较大,对相对电极影响较小。图 7(d)中是不同的电极张角时的差和比变化情况,从图 7中可知,灵敏度(曲线斜率)随张角而增大,从30°-75°的灵敏度分别为6.43 %∙mm-1、6.74 %∙mm-1、7.11 %∙mm-1、7.27 %∙mm-1,虽然增大张角引起了电极间耦合,但对线性区的影响较小。
|
图 7 条带型BPM的CST模拟结果(a)条带型BPM模型,(b)时域信号,(c)频域信号,(d)不同电极张角下的差和比 Figure 7 CST simulation of stripline BPM. (a) Mechanical model, (b) Signal in time domain, (c) Signal in frequency domain, (d)∑/Δwith different pick up angles |
BPM是BEPCII上最重要的束测元件,在机器运行的各个时期都发挥着重要作用,本文主要用CST软件对BPM探头所涉及到的信号强度、灵敏度、转移阻抗以及电极间的耦合进行计算,并针对所用到两种不同类型的BPM进行验证,计算结果表明与实际测量结果符合良好。对于非圆形管道上安装的纽扣型BPM,可以通过调整两个电极之间的水平距离来得到所需的水平、垂直灵敏度。纽扣型BPM的线性区相较小,约为管道中心与电极距离的1/3,通过Mapping图的标定得到更精确的位置信息,拟合时用到的阶数越高,精度越高。条带型BPM的信号比纽扣型更为复杂,其灵敏度比纽扣型大得多,增大电极张角可提高灵敏度,增加的电极间耦合对线性区大小影响不太大。目前的BEPCII的BPM系统运转良好,但是对BPM系统进行深入研究依然有着重要的意义,随着高能光源等项目的开展,更高精度和分辨率的BPM是必不可少的重要一环,利用CST可以帮助设计出性能更加优异的、符合未来加速器需求的BPM。
致谢 感谢德国重离子研究所Peter Forck和上海光源袁仁贤的帮助。| [1] |
Smith S R. Beam position monitor engineering[C]. Proceeding Beam Instrumentation Workshop 1996, AIP Conference Proceedings 390, 1997:50. DOI:10.1063/1.52306.
|
| [2] |
Shafer R E. Beam position monitor[C]. AIP Conference Proceedings 249, 1992:601. DOI:10.1063/1.41980.
|
| [3] |
曹建社, 马力, 麻惠州, 等. Libera BPM在BEPCⅡ调束中的应用[J]. 中国物理C, 2008, 32(增1): 102-104. CAO Jianshe, MA Li, MA Huizhou, et al. Application of Libera BPM at BEPCⅡ for the early commissioning[J]. Chinese Physics C, 2008, 32(S1): 102-104. |
| [4] |
张闯, 马力. 北京正负电子对撞机重大改造工程加速器的设计与研制[D]. 上海: 上海科学技术出版社, 2013. ZHANG Chuang, MA Li. BEPC reconstruction project:the design and development of the accelerator[D]. Shanghai:Shanghai Science and Technology Press, 2013. |
| [5] |
岳军会. BEPCⅡ横向束流反馈系统的研制[D]. 北京: 中国科学院研究生院, 2005. YUE Junhui. Transverse bunch by bunch feedback system for BEPCⅡ[D]. Beijing:Graduate University of Chinese Academy of Sciences, 2005. |
| [6] |
邓庆勇, 曹建社, 叶强, 等. BEPCⅡ储存环束团流强测量[J]. 强激光与粒子束, 2014, 26(7): 075101. Deng Qingyong, CAO Jianshe, YE Qiang, et al. Bunch current measurement system for BEPCⅡ[J]. High Power Laser and Particle Beam, 2014, 26(7): 075101. DOI:10.11884/HPLPB201426.075101 |
| [7] |
邓庆勇. BEPCⅡ储存环逐束团测量研究[D]. 北京: 中国科学院大学, 2015. DENG Qingyong. The research of bunch-by-bunch measurement for BEPCⅡ storage ring[D]. Beijing:University of Chinese Academy of Sciences, 2015. |
| [8] |
麻惠洲. 基于数字束流位置处理器Libera的束测系统的研制[D]. 北京: 中国科学院研究生院, 2009. MA Huizhou. Development of beam diagnostics system based on digital BPM processor Libera[D]. Beijing:Graduate University of Chinese Academy of Sciences, 2009. |
| [9] |
Liu X Y, Yang Y L, Sun B G, et al. Design and simulation of button beam position monitor for IR-FEL[C]. International Particle Accelerator Conference, 2016:187-189.
|
| [10] |
Wu F F, Zhou Z R, Sun B G, et al. Design and calulation of the stripline beam position monitor for HLSⅡ storage ring[C]. International Particle Accelerator Conference, 2013:562-564.
|
| [11] |
Xu J, Yang Y L, Sun B G, et al. Stripline beam position monitor for THz source based FEL[C]. International Particle Accelerator Conference, 2014:3590-3592.
|
| [12] |
Wang B P, Leng Y B, Yu L Y, et al. Design of RF front end for cavity beam position monitor based on ICS[C]. International Beam Instrumentation Conference, 2012:383-385.
|
| [13] |
Chen J, Leng Y B, Yu L Y, et al. Beam experiment of low Q CBPM prototype for SXFEL[C]. International Particle Accelerator Conference, 2016:202-204.
|
| [14] |
Libera brilliance + electron beam position processor[EB/OL]. 2010. http://www.i-tech.si/.
|
| [15] |
Peter F. Lecture notes on beam instrumentation and diagnostics[R]. CERN Accelerator School Beam Diagnostics, 2016.
|
| [16] |
袁任贤. 束流位置测量的研究以及在BEPCⅡ中的应用[D]. 北京: 中国科学院研究生院, 2004. YUAN Renxian. Development of beam diagnostics system based on digital BPM processor Libera[D]. Beijing:Graduate University of Chinese Academy of Sciences, 2004. |
