2. 中国核动力研究设计院 成都 610041
2. Nuclear Power Institute of China, Chengdu 610041, China
板式燃料元件与常规棒式燃料元件的相比具有更大的传热面积,其通道的流动沸腾的换热系数与常规通道相比有很大提高[1]。在反应堆设计中,一些研究用的高通量反应堆通常使用板式燃料元件,这些反应堆的燃料组件会包含一系列的窄缝通道。冷却剂流经这些窄缝通道时将热量带走。窄缝通道由于几何形状与常规圆形通道不同,其流动和换热特性与常规通道有很大差别[2-3],尤其是气泡演化特性和气液两相速度。当大破口事故发生时,注入堆芯的冷却剂对堆芯进行再淹没。再淹没的过程中壁面温度的变化会导致通道中出现不同的流动形态[4]。不同流动形态换热特性之间的巨大差异,增加了数值模拟的复杂性。
模拟再淹没过程通常使用系统程序如Relap5[5]、COBRA-TF等[6]。系统程序通常是用来进行安全分析和复杂系统设计,一维块状网格和经验关系式的使用导致流动和传热的细节被忽略。目前计算流体力学(Computational Fluid Dynamics,CFD)方法进行再淹没的研究相对较少。CFD方法通过求解连续性、动量和能量方程,使用欧拉两流体模型对温度、空泡份额等参数进行求解。通过壁面换热模型对流体和固体之间的换热量进行求解。采用CFD方法计算的几何形状可以更复杂,局部的流动传热信息也更为详尽。
本文首先通过再淹没实验得到固体的温度,之后使用商用CFD软件CFX进行模拟。通过再淹没实验得到了壁面温度对骤冷前沿推进速度及再润湿温度的影响。通过将数值模拟结果与实验值进行比对分析,研究了数值模拟对再淹没过程预测的准确性及不同初始条件对该过程的影响。通过数值模拟得到了平均空泡份额和壁面热流密度分布,以及壁面热流密度最大时的空泡份额。该研究可以从机理上分析再淹没过程,为以后CFD方法开发再淹没计算模型奠定基础。
1 矩形窄通道再淹没实验 1.1 矩形通道再淹没实验简介实验台架THERMAL是矩形窄通道再淹没实验台架,实验循环水温度为(24±1) ℃,流量为(24±1)L∙h-1,壁面初始温度为[(250-500)±1] ℃。实验回路在常压下运行,研究不同初始条件对矩形窄通道中再淹没过程的影响。
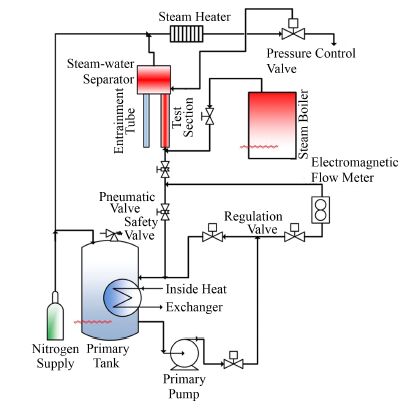
其中实验回路系统图如图 1所示。实验系统由主回路系统和实验回路系统组成。主回路主要用于调节包括进口流速和进口温度等在内的实验初始条件。实验系统主要包括实验段、汽水分离装置、夹带水箱和蒸汽过热器。首先使用陶瓷加热器将实验段加热到指定温度,实验开始时关闭加热器,然后控制气动阀开关改变水的流动方向,使稳定流量的水从实验段底部向顶部流动。实验回路中蒸汽发生器用来产生饱和蒸汽,在实验开始前预热实验回路。实验中再淹没发生时,蒸汽会夹带液体通过汽水分离器。液滴会从汽水分离器中流入夹带水箱。用来观测实验中的夹带量。压力控制阀用于调节系统压力,在高压工况下需要使用该装置。目前尚未进行夹带量和高压工况实验。
|
图 1 再淹没实验系统回路 Figure 1 Schematic diagram of reflooding test facility. |
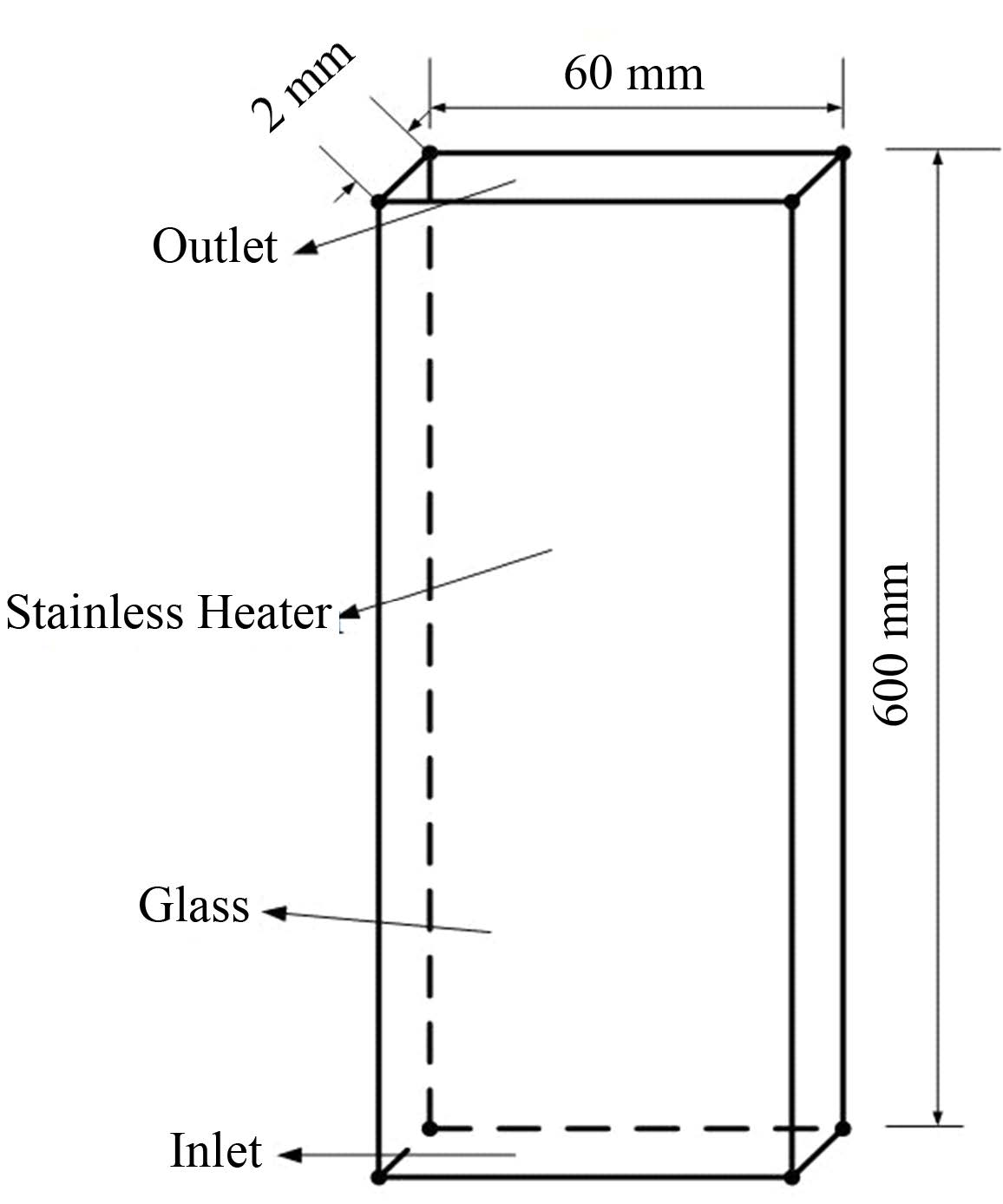
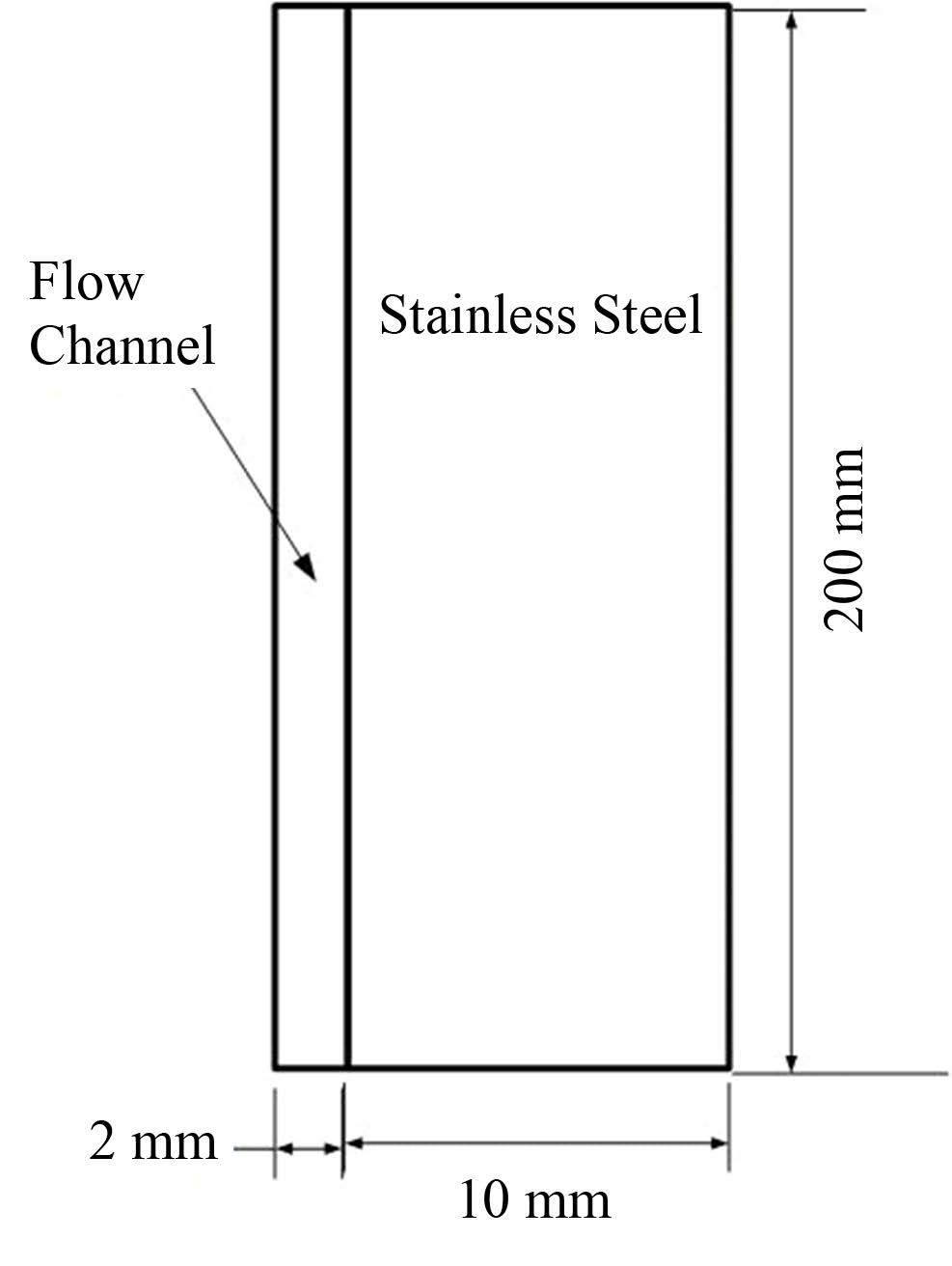
图 2为实验段,图 2中标注的尺寸是窄通道的尺寸。其中流道是由不锈钢板、玻璃和石墨垫片所围成的矩形通道。实验段在实验中由保温材料包围。不锈钢板的厚度为10 mm。流道高度为600 mm,长度为60 mm,宽度为2 mm。
|
图 2 实验段流道示意图 Figure 2 Overview of the test-section. |
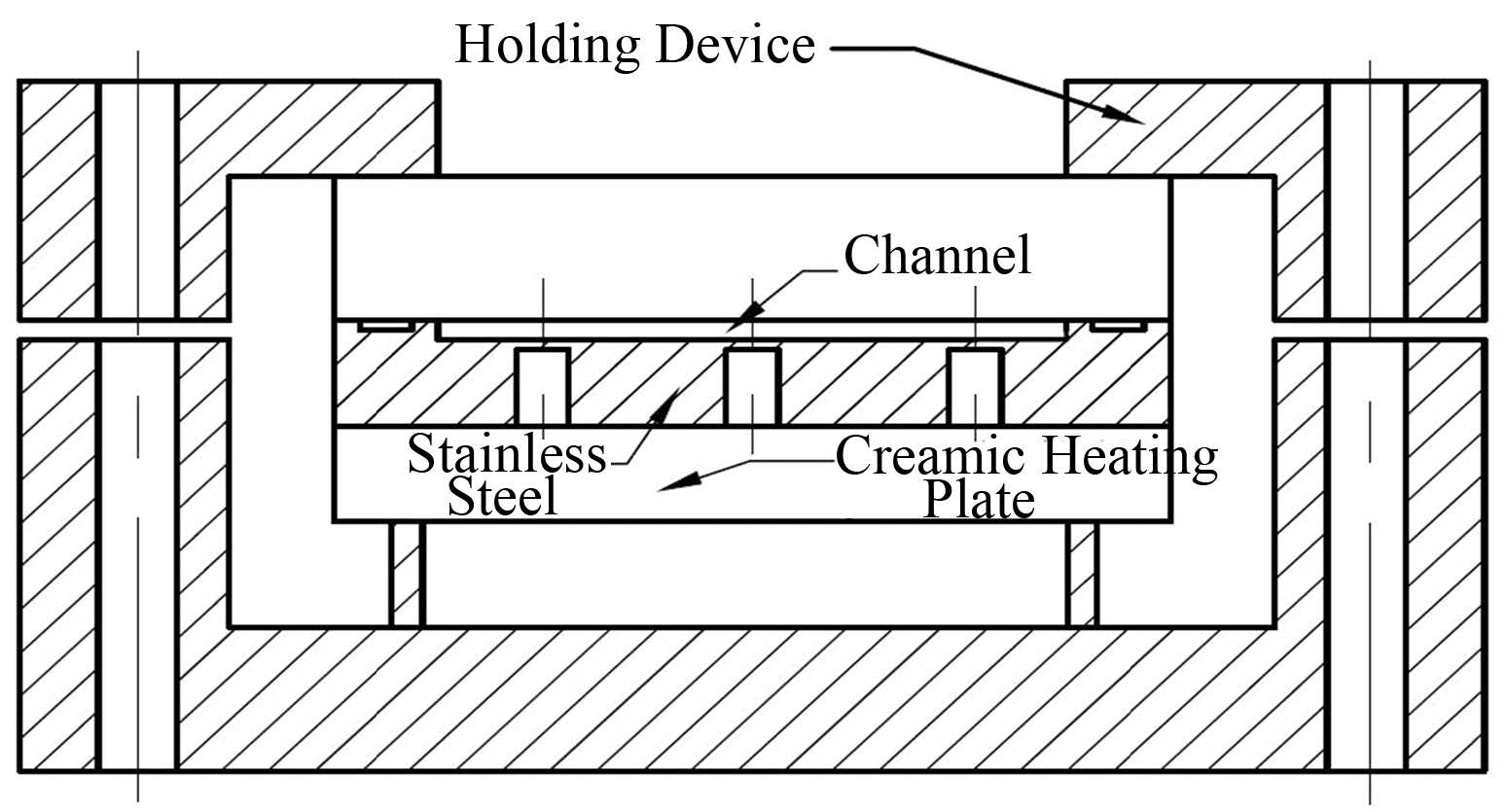
图 3为实验段剖面图,实验中采用陶瓷加热板将不锈钢板加热到指定温度。采用夹持装置来固定玻璃和不锈钢板,以保持流道的密封性。
|
图 3 实验段剖面 Figure 3 View of cross-section of test-section. |
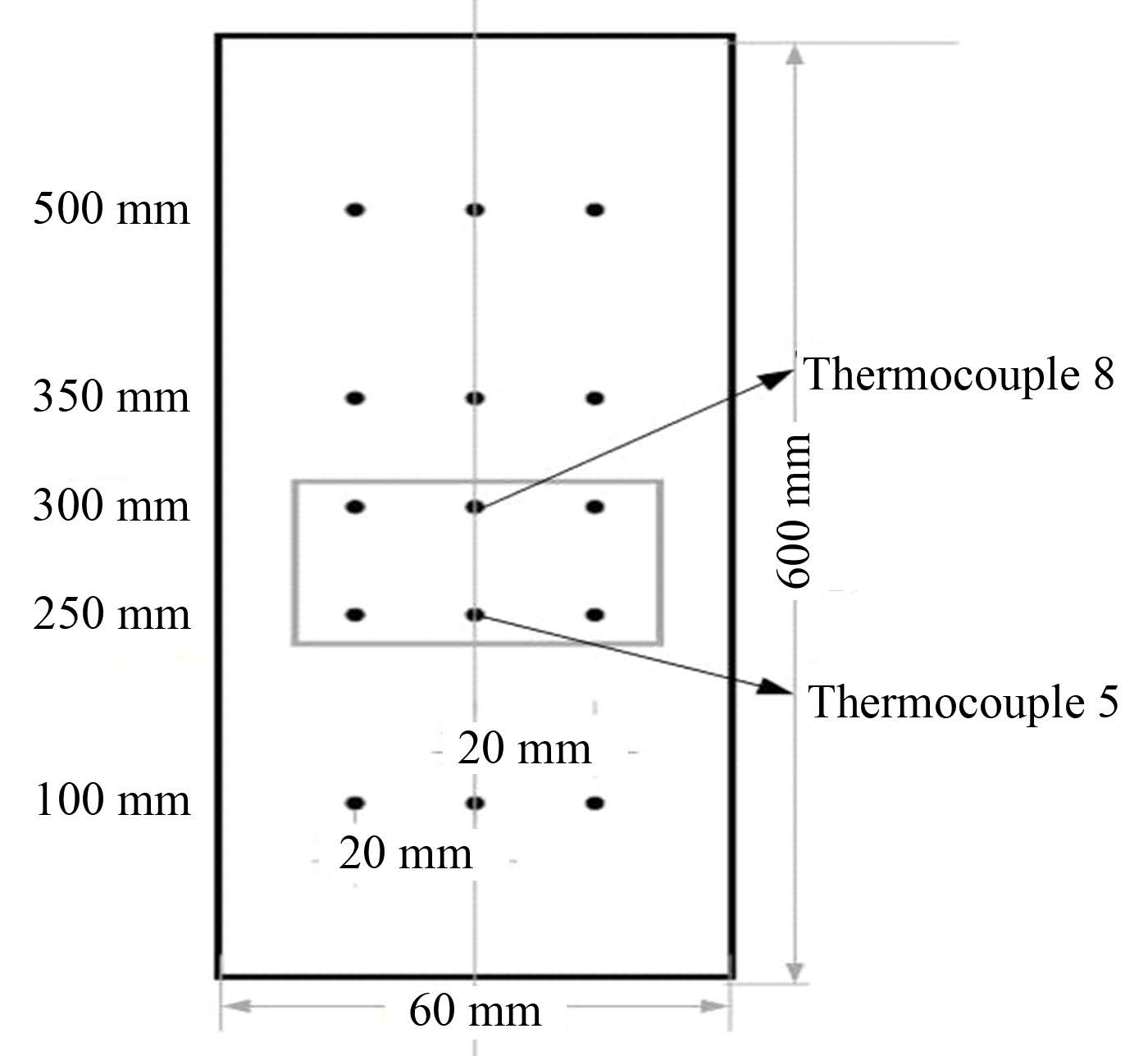
不锈钢温度由热电偶测得,在实验段中有5排,每排3个共15个热电偶。热电偶高度方向上位置分别100 mm、250 mm、300 mm、350 mm、500 mm,图 4为热电偶位置图。热电偶插入的深度为9 mm,即热电偶的测量点距离加热表面为1 mm。由于热电偶测点位置与流固交界面距离较近,数据处理中并未考虑1 mm距离所造成的温差。
|
图 4 热电偶位置 Figure 4 Locations of different thermocouples. |
实验中保持实验段的入口温度不变。通过调节壁面的初始温度和入口流速,从而分析壁面温度和入口流速对再淹没现象的影响。
| 表 1 实验工况 Table 1 Experiment condition. |
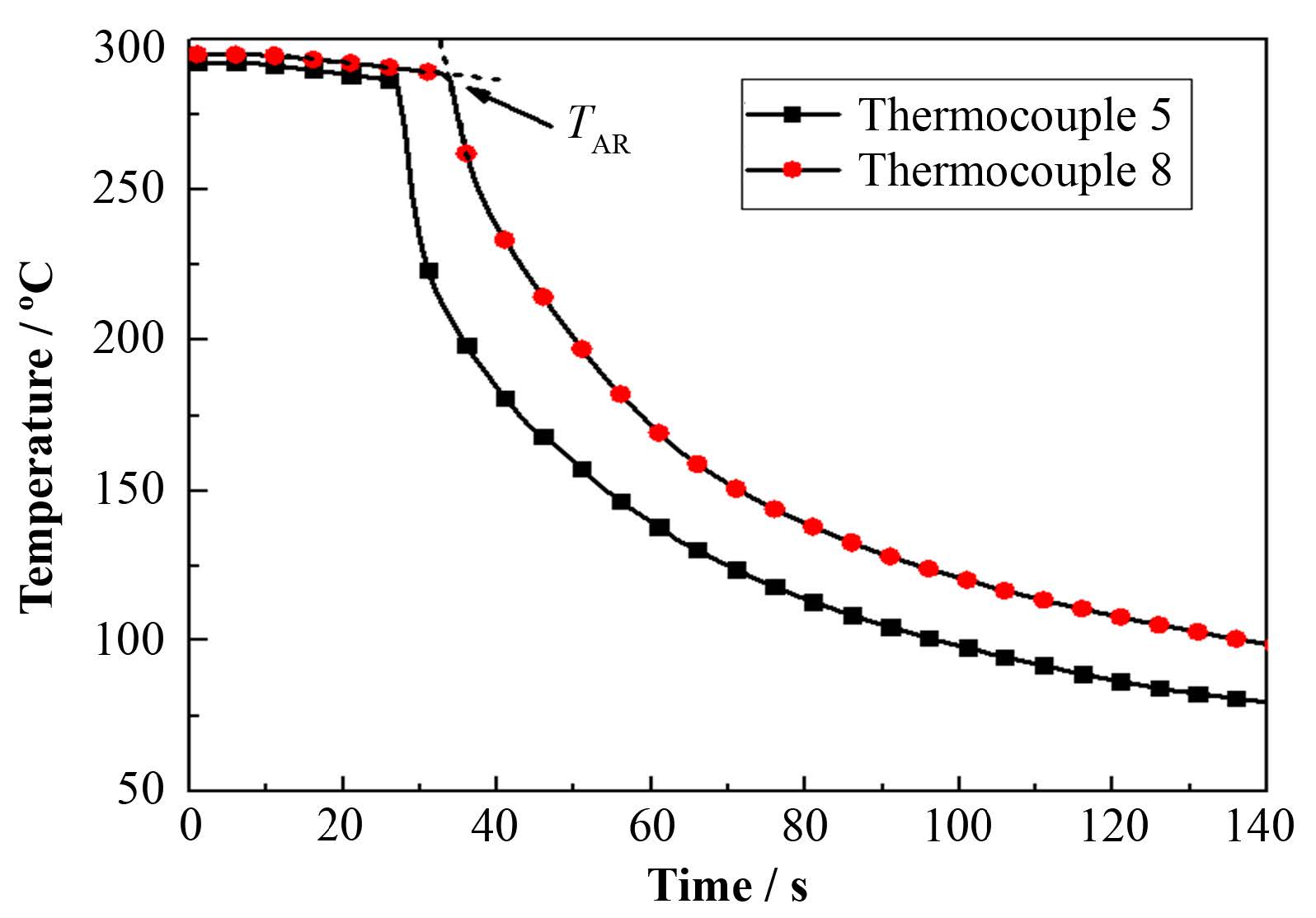
图 5为工况1中热电偶5和热电偶8的温度变化,实验中将壁面温度急剧下降点TAR作为该时刻骤冷前沿位置,根据热电偶5和热电偶8的温度变化计算骤冷前沿推进速度。
|
图 5 工况1中不同位置热电偶温度变化 Figure 5 Temperature variance of different thermocouples in case 1. |
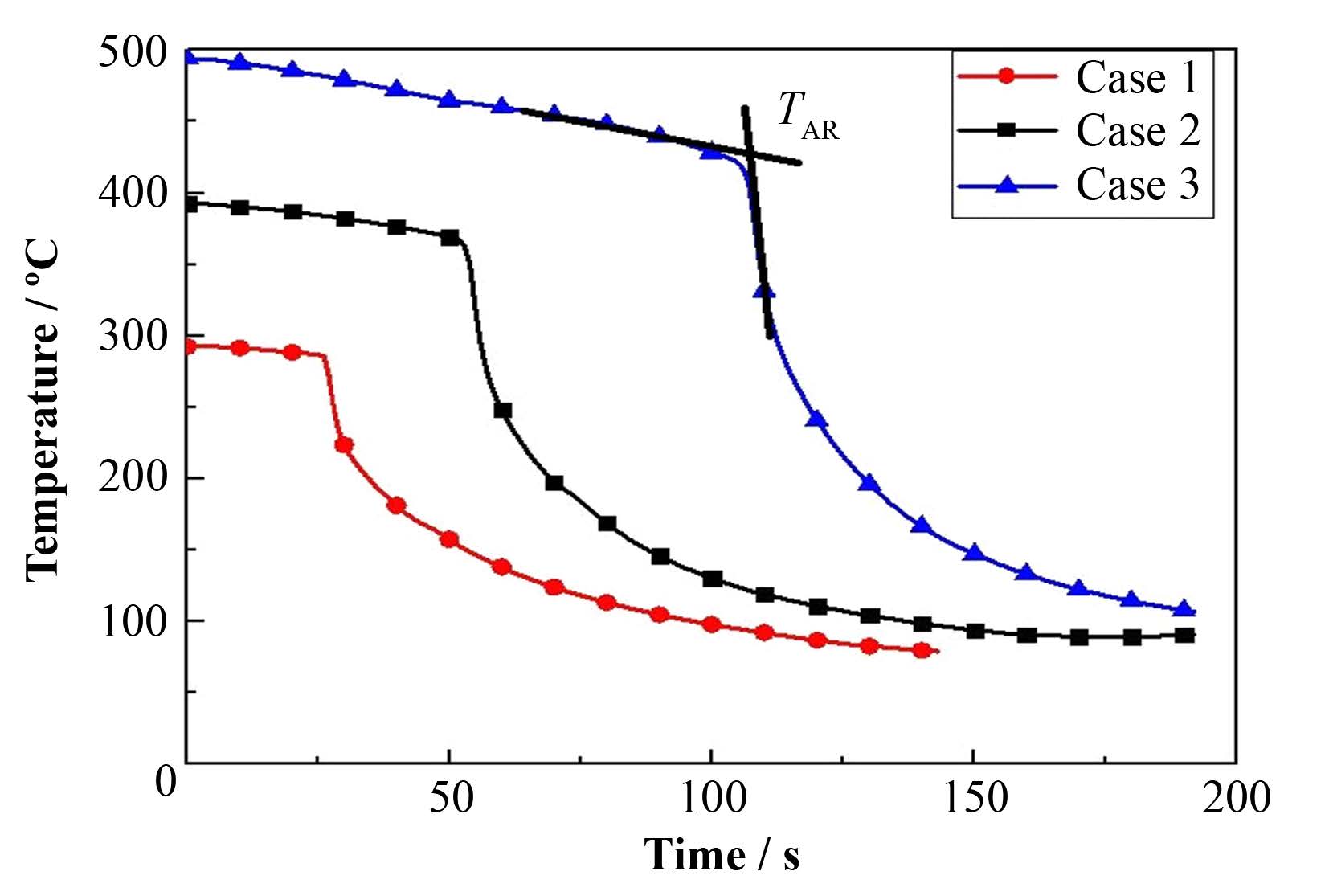
图 6是实验工况中热电偶5位置的壁面温度变化。在工况1-3中,壁面温度分别在31 s、55 s、110s时迅速下降。当壁面温度高于再润湿温度时,此时流动状态为反环状膜态沸腾。之后壁面温度迅速下降,流动状态从过度沸腾转变为核态沸腾,最后转变为单相流动。由图 6可以看出,随着壁面初始温度的增高,骤冷前沿推进速度逐渐降低。工况1-3骤冷前沿推进速度分别为8.06 mm∙s-1、4.54 mm∙s-1、2.27 mm∙s-1。
|
图 6 不同初始壁面温度热电偶温度变化 Figure 6 Temperature variance of thermocouples at different surface temperature. |
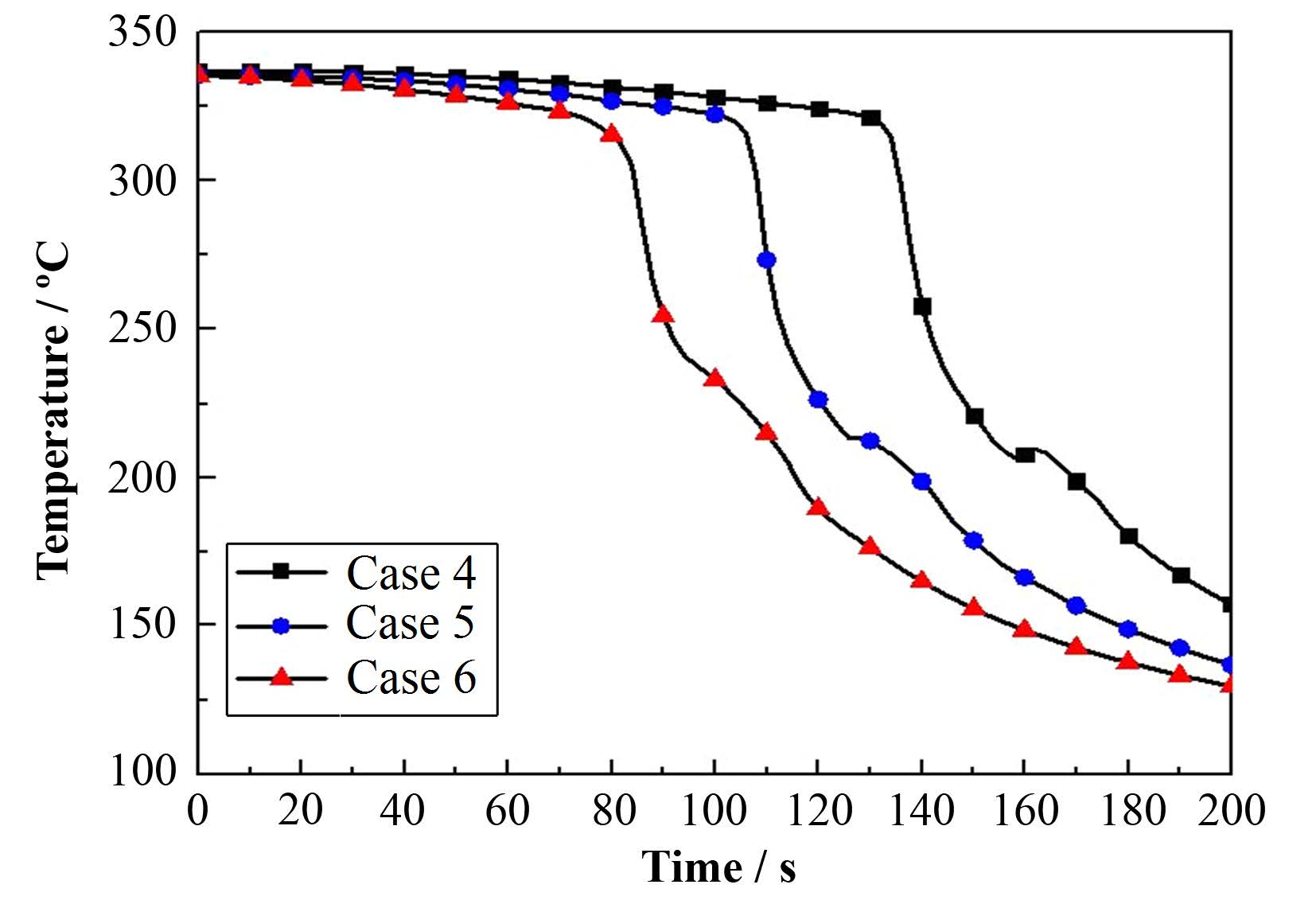
图 7是工况4-6中热电偶5温度分布。从图 7中可以看出,随着入口流速的增加,骤冷前沿推进速度逐渐增加。这是由于入口流速增加时,液滴的夹带量增加,先驱冷却过程换热增强,从而使壁面温度先降到骤冷温度,之后再润湿发生。
|
图 7 不同入口流速热电偶温度变化 Figure 7 Temperature variance of thermocouples at different inlet velocity. |
从以上实验数据可知,再淹没过程中骤冷前沿推进速度与初始壁面温度和入口流速有关。初始壁面温度增高时,骤冷前沿推进速度减小。入口流速增大时,骤冷前沿推进速度增大。
1.4 再润湿温度再润湿温度是指液体可以重新接触干燥的固体表面时刻的温度[7]。当表面温度冷却到两相流动流型发生变化,从膜态沸腾到过渡沸腾或核态沸腾时,即再润湿发生。在图 6中TAR表示工况3中的再润湿温度,即骤冷前温度曲线的切线与温度曲线斜率绝对值最大点的切线的交叉点。从图 6中可以看出,再润湿温度与壁面初始温度有关,壁面初始温度增高时,再润湿温度增高。而对比图 7中不同入口流速情形,当入口流速改变时,再润湿温度几乎不变。
2 数学模型 2.1 欧拉两流体模型在CFD两相计算中,欧拉两流体的模型被广泛的应用于CFD两相计算。欧拉两流体模型有以下优点:可以得到全局的参数、适用的体积分数范围比较大、计算量相对较少。
质量守恒方程:
| $\frac{\partial }{\partial t}\left( {{r}_{\alpha }}{{\rho }_{\alpha }} \right)+\nabla \cdot \left( {{r}_{\alpha }}{{\rho }_{\alpha }}{{U}_{\alpha }} \right)={{S}_{MS\alpha }}+\sum\limits_{\beta =1}^{{{N}_{p}}}{{{\Gamma }_{\alpha \beta }}}$ | (1) |
式中:rα为体积份额;SMSα为质量源项;Γαβ为从α到β相的质量流密度。
动量守恒方程:
| $\begin{align} & \frac{\partial }{\partial t}\left( {{r}_{\alpha }}{{\rho }_{\alpha }} \right)+\nabla \cdot \left( {{r}_{\alpha }}\left( {{\rho }_{\alpha }}{{U}_{\alpha }}\otimes {{U}_{\alpha }} \right) \right)= \\ & -{{r}_{\alpha }}\nabla {{\rho }_{\alpha }}+\nabla \left( {{r}_{\alpha }}{{\mu }_{\alpha }}\left( \nabla U_{\alpha }^{T} \right) \right)+\sum\limits_{\beta =1}^{{{N}_{p}}}{\left( \Gamma _{\alpha \beta }^{+}{{U}_{\beta }}-\Gamma _{\beta \alpha }^{+}{{U}_{\alpha }} \right)} \\ & +{{S}_{M\alpha }}+{{M}_{\alpha }} \\ \end{align}$ | (2) |
式中:SMα为动量源项;Mα为表面力对α相的作用力。
能量守恒方程:
| $\begin{align} & \frac{\partial }{\partial t}\left( {{r}_{\alpha }}{{\rho }_{\alpha }}{{h}_{\alpha }} \right)+\nabla \cdot \left( {{r}_{\alpha }}{{\rho }_{\alpha }}{{U}_{\alpha }}{{h}_{\alpha }} \right)= \\ & \nabla \cdot \left( {{r}_{\alpha }}{{\lambda }_{\alpha }}\nabla \cdot {{T}_{\alpha }} \right)+{{r}_{\alpha }}\nabla \cdot \left( {{U}_{\alpha }}{{\tau }_{\alpha }} \right)+ \\ & {{S}_{E\alpha }}+{{Q}_{\alpha }}+\sum\limits_{\beta =1}^{{{N}_{p}}}{\left( \Gamma _{\alpha \beta }^{+}{{h}_{\beta s,tot}}-\Gamma _{\beta \alpha }^{+}{{h}_{\alpha s,tot}} \right)} \\ \end{align}$ | (3) |
式中:SEα为外部热源;Qα为其它相通过相间对α相的传热。
2.2 相间作用力模型由于考虑到再淹没过程中流型的变化比较复杂,相间作用力模型采用Mixture模型。相间曳力的表达式为:
| ${{D}_{\alpha \beta }}={{C}_{d}}{{\rho }_{\alpha \beta }}{{A}_{\alpha \beta }}\left| {{U}_{\beta }}-{{U}_{\alpha }} \right|\left( {{U}_{\beta }}-{{U}_{\alpha }} \right)$ | (4) |
式中:Cd为无量纲的曳力系数。其中混合项密度为:
| ${{\rho }_{\alpha \beta }}={{r}_{\alpha }}{{\rho }_{\alpha }}+{{r}_{\beta }}{{\rho }_{\beta }}$ | (5) |
相间传热面积为:
| ${{A}_{\alpha \beta }}=\frac{{{r}_{\alpha }}{{r}_{\beta }}}{{{d}_{\alpha \beta }}}$ | (6) |
式中:dαβ为定义的混合尺度。
2.3 相间能量传递模型在气相和液相的交界面,用一个总的换热系数来表示相间界面的换热系数hαβ。
相间的换热表达式如下:
| ${{Q}_{\alpha \beta }}={{h}_{\alpha \beta }}{{A}_{\alpha \beta }}\left( {{T}_{\beta }}-{{T}_{\alpha }} \right)$ | (7) |
在Mixture模型中,换热系数hαβ描述为混合导热系数与混合尺度的函数:
| ${{h}_{\alpha \beta }}=\frac{{{\lambda }_{\alpha \beta }}N{{u}_{\alpha \beta }}}{{{d}_{\alpha \beta }}}$ | (8) |
式中:λαβ=rαλα+rβλβ。
2.4 壁面沸腾模型在近壁面,采用了计算壁面沸腾最常用的美国伦斯勒理工学院模型(Rensselaer Polytechnic Institute,RPI)[8]。在RPI模型中,壁面的换热量被认为是三个量的积分。其中当流体的温度超过饱和温度时,流体就会发生相变。
| ${{Q}_{tot}}={{Q}_{c}}+{{Q}_{q}}+{{Q}_{e}}$ | (9) |
式中:Qtot为壁面总换热量;Qc为单相对流换热项;Qq为骤冷换热项;Qe为蒸发项。
2.4.1 单相对流项式(10)中Qc为通过对流通过壁面传递的热量,表达式如下:
| ${{Q}_{c}}=\left( 1-{{A}_{bubble}} \right){{h}_{c}}\left( {{T}_{w}}-T_{nw}^{+} \right)$ | (10) |
式中:Abubble为被气泡占据的壁面份额;Tw为壁面温度;为近壁面流体的温度。其中对流换热系数hc采用Kader壁面温度函数关系式计算得到。其计算关系式如下:
| ${{h}_{c}}=\frac{{{\rho }_{L}}{{C}_{P,L}}{{u}_{\tau }}}{T_{nw}^{+}}$ | (11) |
式中:ρL是液相密度;Cp,L是液相等压比热容;uτ是壁面剪切速度;由Kader的温度壁面函数关系式求得,即:
| $\begin{align} & T_{nw}^{+}=\Pr {{y}^{+}}{{e}^{-\Gamma }}+ \\ & \left\{ 2.12\ln \left[ \left( 1+{{y}^{+}} \right)\frac{2.5\left( 2-{y}/{\delta }\; \right)}{1+4\left( 1-{y}/{\delta }\; \right)} \right]+\beta \left( \Pr \right) \right\}{{e}^{{-1}/{\Gamma }\;}} \\ \end{align}$ | (12) |
| $\Gamma =\frac{0.04{{\left( \Pr {{y}^{+}} \right)}^{4}}}{1+5{{\Pr }^{3}}{{y}^{+}}}$ | (13) |
骤冷项Qq的表达式如下:
| ${{Q}_{q}}={{A}_{bubble}}{{h}_{q}}\left( {{T}_{w}}-T_{nw}^{+} \right)$ | (14) |
其中骤冷项换热系数hq为:
| ${{h}_{q}}=2{{\lambda }_{1}}f\sqrt{\frac{{{t}_{w}}}{\pi {{a}_{1}}}}$ | (15) |
| $f=\sqrt{\frac{4g\left( {{\rho }_{1}}-{{\rho }_{g}} \right)}{3{{C}_{d}}{{d}_{w}}{{\rho }_{1}}}}$ | (16) |
twait为气泡等待时间:
| ${{t}_{wait}}=\frac{0.8}{f}$ | (17) |
气泡影响面积为:
| ${{A}_{bubble}}=\min \left( \frac{\pi {{F}_{2}}^{2}d_{w}^{2}}{4}n,1 \right)$ | (18) |
式中:F2是一个可以调节的影响因素,默认值为2。dw为气泡脱离直径,根据Kurul和Podowski提出将气泡脱离直径采用如下关系式:
| ${{d}_{w}}=\min \left( {{d}_{ref}}\exp \left( -\frac{\Delta {{T}_{sub}}}{\Delta {{T}_{ref}}} \right),{{d}_{\max }} \right)$ | (19) |
式中:dmax=1.4 mm,dref=0.6 mm,Tref=45 K。
2.4.3 蒸发项蒸发项的Qe表达式如下:
| ${{Q}_{e}}=\frac{\pi d_{w}^{3}}{6}{{\rho }_{g}}fn{{h}_{fg}}$ | (20) |
式中:n为气化核心密度,其表达式为:
| $n={{n}_{ref}}{{\left( {\Delta {{T}_{\sup }}}/{\Delta {{T}_{ref}}}\; \right)}^{p}}$ | (21) |
式中:nref=0.8×9.922×105 m-2;ΔTsup=min[max (Twall-Tsat,0),ΔTmax];ΔTref=10 K;p=1.8;ΔTmax是为了防止在初始收敛过程中发生溢出而设置的壁面过热度最大值,默认值为25 K。
3 CFD二维计算模型图 8为CFD计算几何模型。
|
图 8 CFD计算几何模型 Figure 8 CFD geometry. |
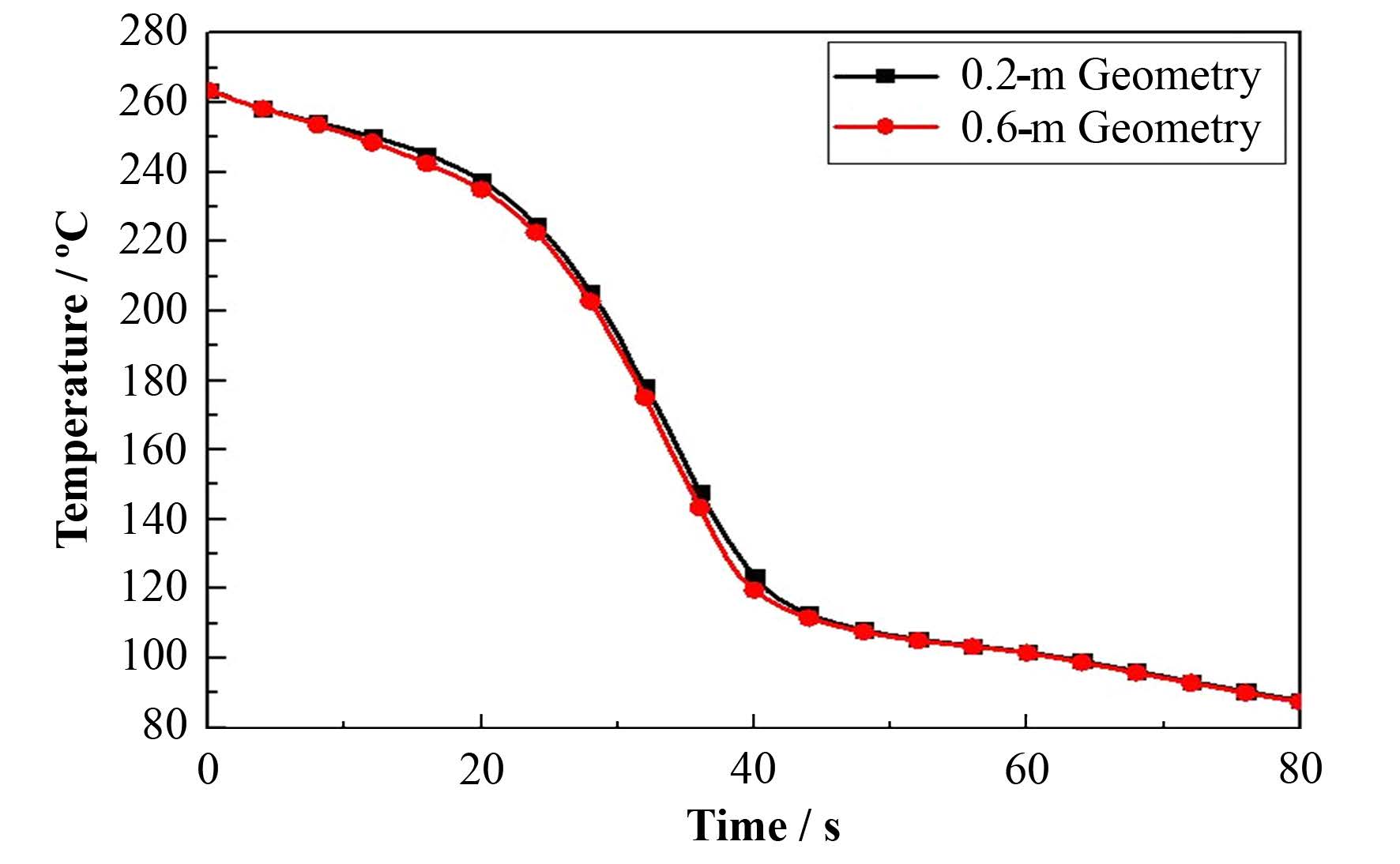
数值模拟中入口为流速入口,出口为压力出口,其他边界均为绝热边界。不锈钢固体给定初始温度进行瞬态模拟。由于实验段长度较长,进口流速较小,且骤冷前沿的上部固体温度变化较小。骤冷前沿上部固体对下部的导热与再淹没过程中固体与流体的对流换热相比很小。为了提高计算效率,将CFD计算几何模型高度简化为0.2 m。根据网格敏感性分析,计算中采用20×5的网格。该网格计算得到的温度变化最接近实验值。图 9是使用0.6 m与0.2 m的几何得到的壁面温度分布对比。图 9中温度点的位置高0.1 m中间热电偶位置。后面的计算中也取该点作为参考点。从图 9中可以看出,采用 0.2 m的几何与采用0.6 m的几何计算得到的在0.1 m位置中间热电偶测点的温度分布几乎没有差别,为了提高计算速度,采用0.2 m的几何进行后续计算。
|
图 9 0.2 m与0.6 m的几何温度变化 Figure 9 Temperature difference between 0.2-m and 0.6-m geometry. |
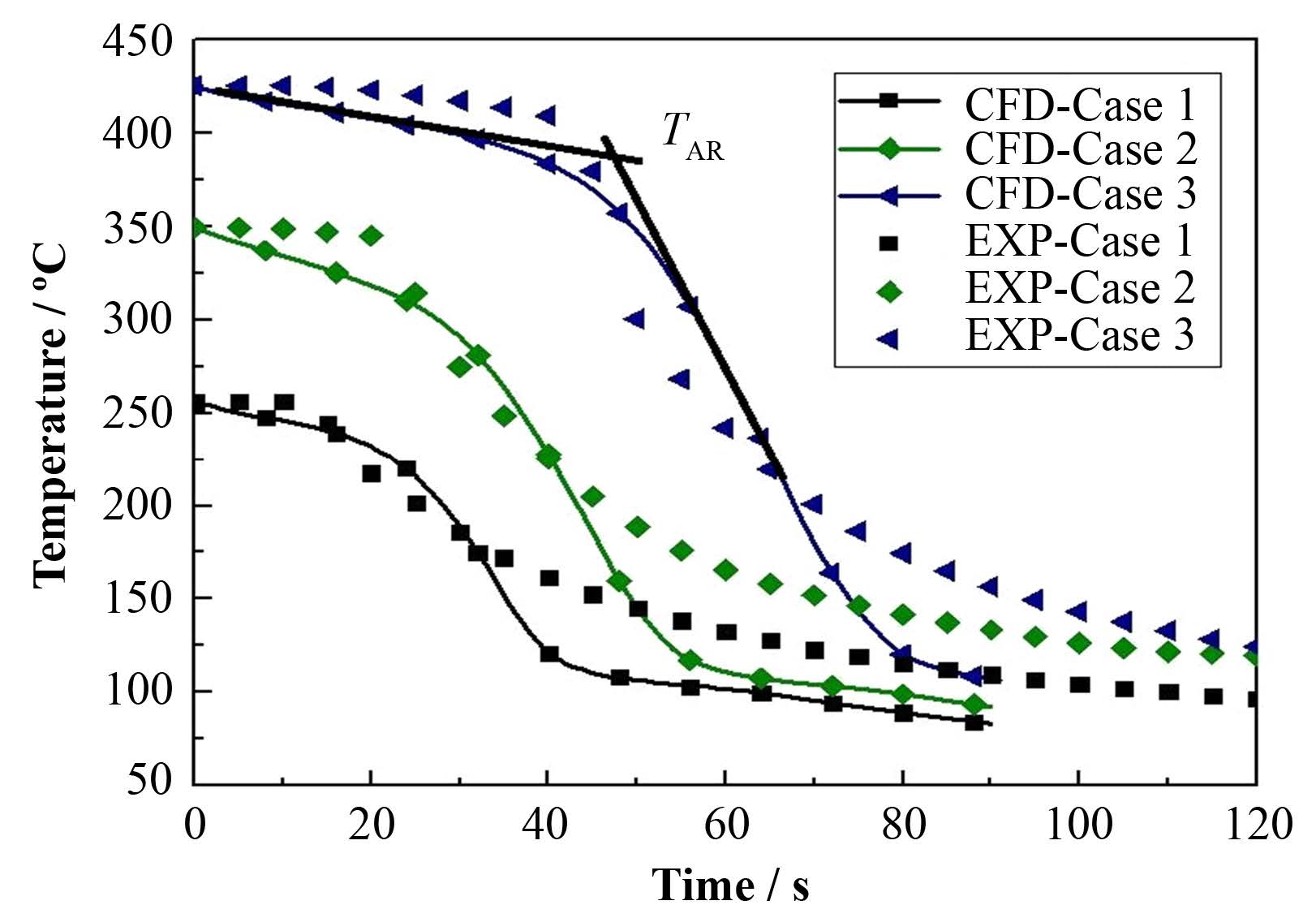
图 10为实验结果和数值模拟结果在指定点的温度变化。通过图 10对比模拟结果和实验结果可以发现,数值模拟对骤冷前沿推进速度和再润湿温度的估计与实际值趋势一致,但细节上有一定差别。在工况1中,t=13 s时骤冷前沿已经推进至热电偶的位置,而在模拟中直到约23 s后壁面温度才开始大幅的下降。在工况2结果中,t=25 s时骤冷前沿已经推进至热电偶的位置,而模拟中直到约32 s壁面温度开始大幅下降。在工况3中,t=47s骤冷前沿推进至热电偶位置,而数值模拟中到约53 s时壁面温度开始迅速下降。
|
图 10 不同初始壁温指定点温度比较 Figure 10 Temperature comparison of the given point at different surface temperature. |
通过实验与数值模拟对比可以发现,数值计算对再淹没过程中壁面温度预测的趋势与实验值一致。但在数值模拟中,壁面温度的下降趋势比实验值快,这是由于数值模拟对壁面换热的估计比真实值大。而壁面换热估计比真实值大的原因可能是窄通道壁面气泡生成对换热的阻碍较大,而数值计算中难以模拟这一现象。在流动初期,数值模拟与实验温度较为接近,而在流动末期,数值模拟中壁面温度下降较快,而实验中壁面温度下降缓慢。这是由于RPI模型需设置湍流流动,而实际流动由于入口流速较低,雷诺数较低,流动后期主要为层流流动。数值模拟对于再润湿温度的预测普遍偏低,这可能是由于数值模拟对壁面换热估计过大。
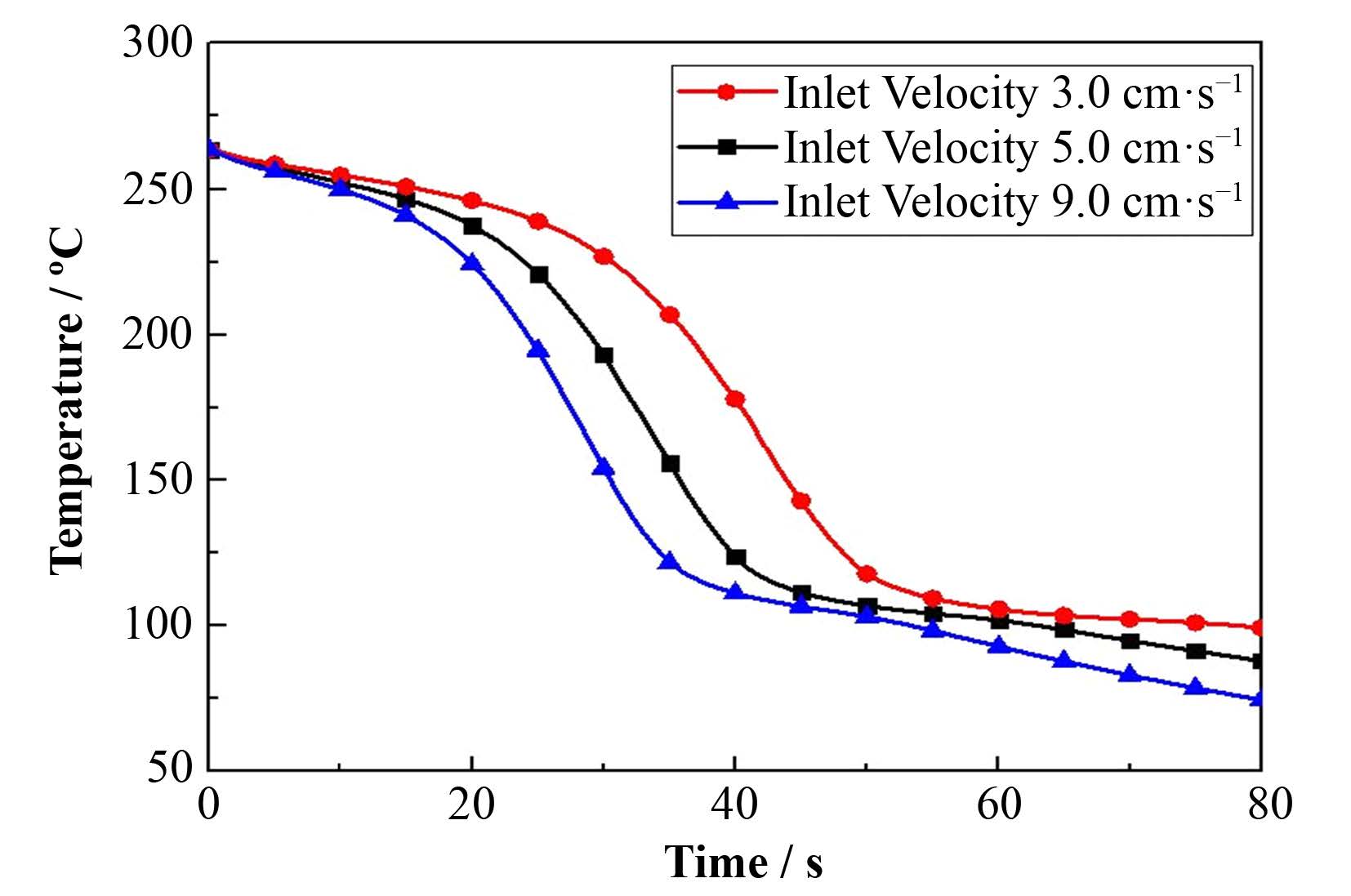
通过图 11对比不同入口流速的数值模拟结果可以发现,入口流速对骤冷前沿推进速度存在影响。当入口流速较快时,骤冷时间较短,再润湿温度降低。
|
图 11 不同入口流速指定点温度比较 Figure 11 Temperature comparison of the given point at different inlet velocity. |
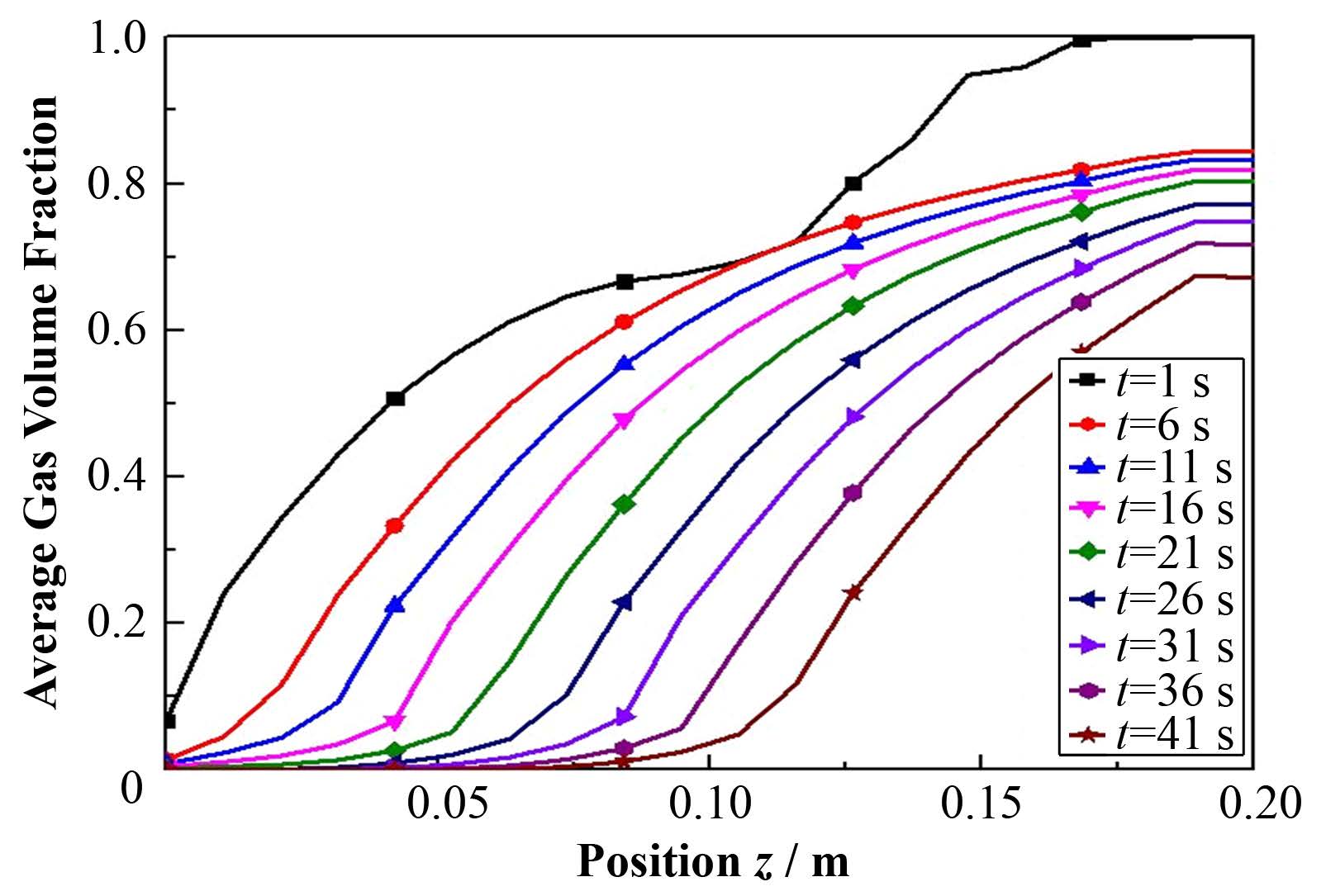
图 12是数值模拟实验工况1中通道内水平方向的平均空泡份额在竖直方向的瞬态分布曲线。通过对比该图可以发现,在不同位置气体空泡份额有很大变化。进口处空泡份额较小,而出口处空泡份额较大。由于瞬态计算,初始时刻计算的不稳定导致t=1 s时刻曲线的波动。之后随着时间的增长,该曲线几乎平行向右移动。
|
图 12 空泡份额随时间变化分布 Figure 12 Volume fraction variance with time. |
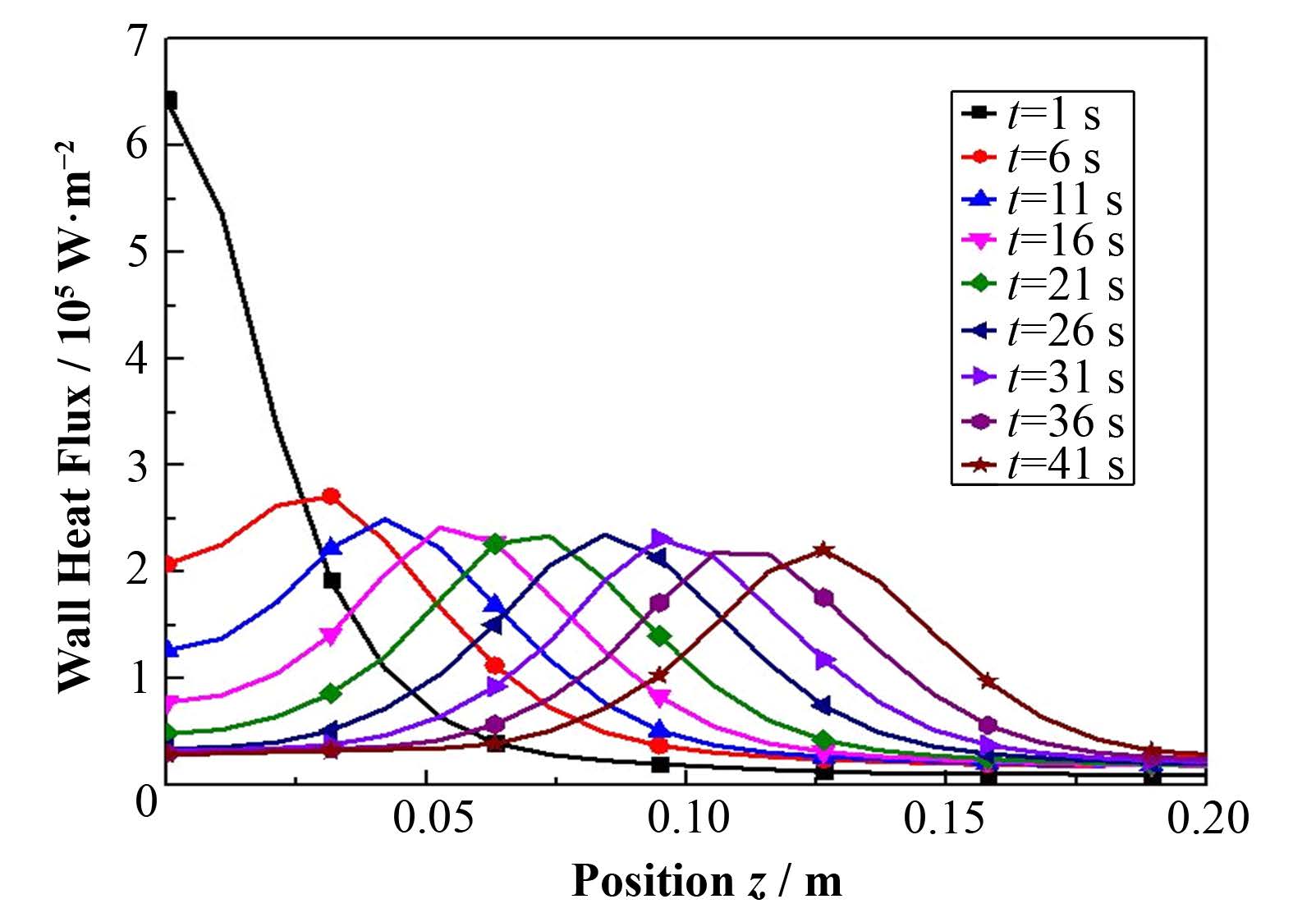
通过图 13对比数值模拟实验工况1中不同时刻壁面热流密度在竖直方向上分布可以发现,在轴向不同位置壁面热流密度在(0.4-6.5)×105 W∙m-2变化。随着时间的增长,热流密度的最高点随着骤冷前沿的推进逐渐向流道顶部移动。
|
图 13 壁面热流密度随时间变化分布 Figure 13 Heat flux density variance with time |
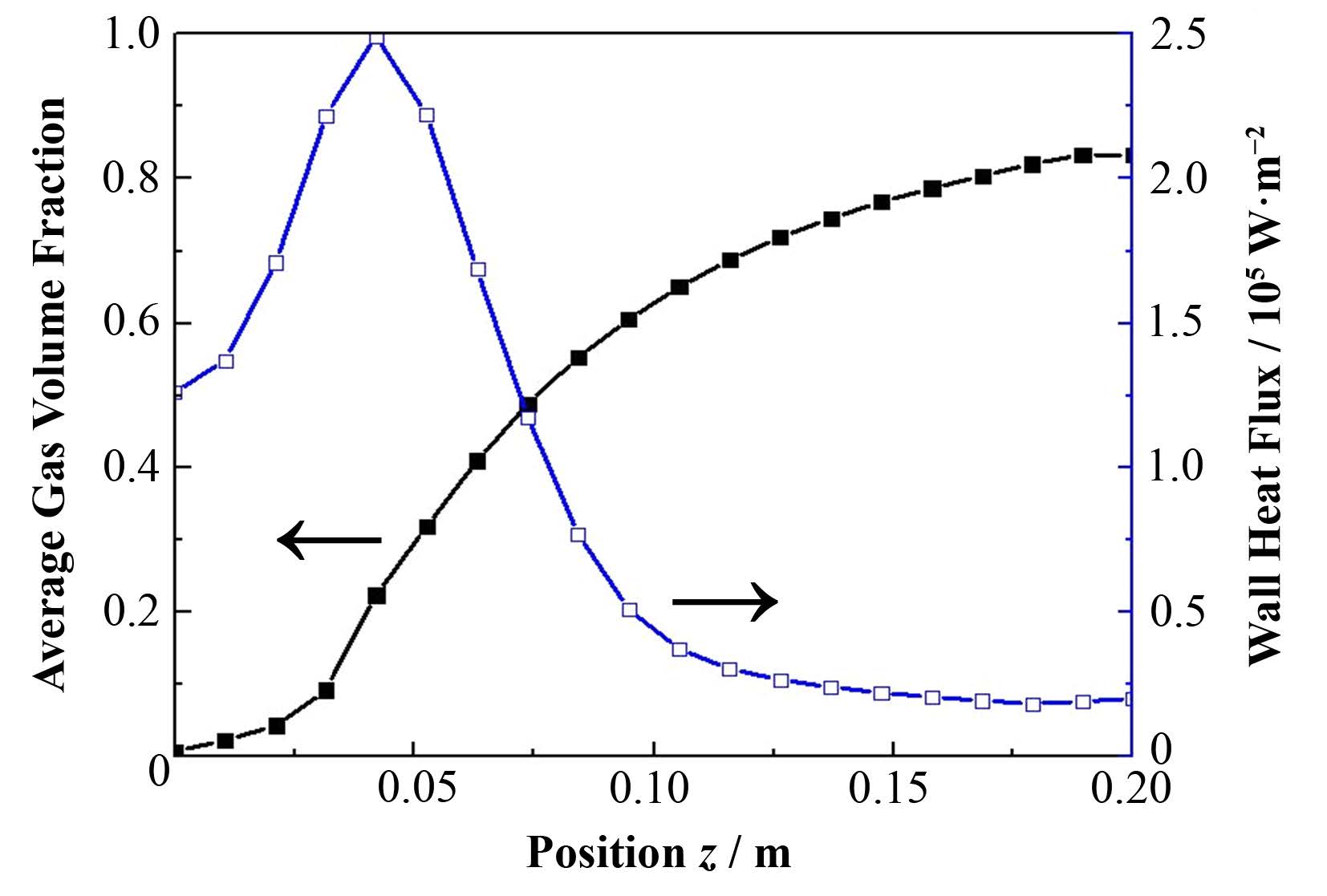
图 14是t=11 s时水平方向的平均空泡份额分布和壁面热流密度分布,通过对比图 11可以发现壁面热流密度最大处的空泡份额约为0.3。
|
图 14 11 s时刻空泡份额与壁面热流密度分布 Figure 14 Volume fraction and heat flux density distributions in t=11 s. |
本文通过矩形窄通道再淹没现象实验和数值研究得到如下结论:CFD方法在预测再淹没现象中得到的壁面温度变化趋势与实验值一致。但数值模拟中对壁面换热和再润湿温度的估计要小于实验值。这可能是矩形窄通道中再淹没过程中壁面气泡生成对换热的阻碍较大,而数值计算中难以模拟这一现象。实验过程发现壁面温度增高,骤冷前沿推进速度降低,再润湿温度升高。入口流速减小,骤冷前沿推进速度降低,再润湿温度不变。数值模拟可知流道空泡份额与壁面热流密度分布曲线随时间的增长,不断向流道顶部移动,在壁面热流密度最大时空泡份额约为0.3。
通过本研究得到了骤冷前沿推进速度与再润湿温度的数值。这些实验值将应用于计算板式元件反应堆大破口事故情形下再淹没时间及包壳温度,为提高计算准确性打下基础。
后续的研究将会尝试改变RPI模型中一些子模型,从而更加准确的预测再淹没过程。
| [1] |
陈冲, 高璞珍, 谭思超, 等. 竖直窄矩形通道内环状流的流动传热特性[J].
化工学报
, 2015, 66(2): 537–544.
CHEN Chong, GAO Puzhen, TAN Sichao, et al. Flow and heat transfer characteristics of annular flow in vertical rectangular narrow channel[J]. CIESC Journal, 2015, 66(2): 537–544. |
| [2] |
董化平, 樊文远, 郭赟. 板状燃料组件流量分配CFD研究与优化[J].
核技术
, 2016, 39(8): 080603.
DONG Huaping, FAN Wenyuan, GUO Yun. CFD investigation and optimization on flow distribution of plate-type assembly[J]. Nuclear Techniques, 2016, 39(8): 080603. DOI: 10.11889/j.0253-3219.2016.hjs.39.080603 |
| [3] | Qu X X, Zhang Y J, Ji H J, et al. Experimental research on velocity distribution in narrow slots of plane type reactor fuel[J]. Atomic Energy Science and Technology, 2003, 37(6): 519–522. |
| [4] | Lokanathan M, Hibiki T. Flow regime, void fraction and interfacial area transport and characteristics of co-current downward two-phase flow[J]. Nuclear Engineering and Design, 2016, 307(1): 39–63. |
| [5] |
曾未, 余红星, 孙玉发, 等. 基于RELAP5的窄缝通道再淹没模型适应性研究[J].
核动力工程
, 2013, 34(3): 50–57.
ZENG Wei, YU Hongxing, SUN Yufa, et al. Research on reflooding model of narrow channel based on RELAP5[J]. Nuclear Power Engineering, 2013, 34(3): 50–57. |
| [6] | Moon S K, Kim J, Kim K, et al. Reflood experiments in rod bundles with flow blockages due to clad ballooning[J]. Kerntechnik, 2016, 81(3): 251–256. DOI: 10.3139/124.110744 |
| [7] | Debbarma A, Pandey K M. Influence on rewetting temperature and wetting delay during rewetting rod bundle by various radial jet models[J]. Kerntechnik, 2016, 81(1): 50–59. DOI: 10.3139/124.110571 |
| [8] | Mohamedi B, Hanini S, Ararem A, et al. Simulation of nucleate boiling under ANSYS-FLUENT code by using RPI model coupling with artificial neural networks[J]. Nuclear Science and Techniques, 2015, 26(4): 040601. DOI: 10.13538/j.1001-8042/nst.26.040601 |
| [9] | Končar B, Matkovič M. Simulation of turbulent boiling flow in a vertical rectangular channel with one heated wall[J]. Nuclear Engineering and Design, 2012, 245: 131–139. DOI: 10.1016/j.nucengdes.2012.01.013 |
| [10] |
李权, 焦拥军, 于俊崇. 竖直加热圆管内过冷沸腾及CHF数值模拟[J].
核动力工程
, 2015, 36(1): 168–172.
LI Quan, JIAO Yongjun, YU Junchong. Simulation of subcooled boiling and critical heat flux in uniformly heated tube[J]. Nuclear Power Engineering, 2015, 36(1): 168–172. |


