反应堆为用户提供中子束辐照服务时，需要为用户提供中子能谱、中子注量等中子场特性数据。中子注量的测量分为在线测量和离线测量两类^[1]。在线测量仪器一般采用气体探测器、闪烁探测器及半导体探测器等；离线方法有活化法、固体径迹方法等。活化法监测中子注量^[2]具有灵活性好、对中子场扰动小、灵敏度宽等优势。对于辐射效应实验所关心的快中子，美国材料与试验协会(American Society for Testing and Materials,ASTM)标准^[3-5]推荐铁、硫、镍作为快中子注量监测活化箔。铁、硫、镍等活化箔应用广泛^[6-7]，但均为阈探测器，有效的中子探测阈值都高于2MeV。对于西安脉冲堆辐照腔中子能谱，即便使用辐照装置过滤热中子，能量在2MeV以上的中子也只占到中子注量的20%^[8]，因此，这些活化箔在测量这种能谱较软的中子注量时，对能量在2MeV以下的绝大多数中子都是依靠中子能谱外推得到的。如果中子能谱在2MeV以下误差较大，那么测量数据会存在较大偏差。

¹⁰³Rh(n,n′)¹⁰³Rh^m反应中子灵敏能区在0.1-10MeV之间，覆盖了西安脉冲堆辐照装置内90%以上的快中子，在能量覆盖范围上相比以上几种反应有优势，可以作为快中子注量监测活化箔应用^[9]，但未见具体测量方法报道。本文阐述了一种利用¹⁰³Rh(n,n′)¹⁰³Rh^m反应监测快中子注量的具体实现方法，将测量结果与其他活化箔结果进行对比，并对不确定度进行了讨论。

若已知测量中子能谱分布，可选用反应阈值大于E₀的活化箔测量E>E₀的快中子注量，在反应堆稳态运行工况下，辐照时间t_r内，快中子注量为：

式中：为Φ_E0>E₀的快中子注量，n·cm⁻²；A为箔测量活化率，s⁻¹$\bar \sigma $_E0为E>E₀中子活化箔谱平均截面，cm²。

$\bar \sigma $_E0定义为：

式中：$\phi (E)$为已知能谱给出的单位能量范围内中子注量率，n·cm⁻²·eV⁻¹·s⁻¹。

将式(2)离散化，得到：

式中：${\phi _K}$为第k群中子注量率，n·cm⁻²·s⁻¹；${\sigma _K}$为第k群反应截面，cm²。

同时，设c为净全能峰计数；γ_d为g射线分支比；ε为谱仪对源的探测效率；θ₀为阿佛加得罗常数；t_c为谱仪测量γ峰的计数时间；M为天然元素的原子量；q为受照射核素的同位素丰度；m为箔的质量；m₀为箔辐照前靶核数；λ为产生核素的衰变常数；t_irr为箔被辐照的时间；t_w为箔冷却时间；k_t为高纯锗γ谱仪死时间校正因子；k_s为箔自吸收校正因子；${\bar \sigma _{mn}}$为核反应的谱平均截面；$\phi $为中子积分通量。

活化箔辐照后，其活度为：

经过冷却t_w后，其活度为：

在谱仪对活化箔进行t_c时间测量后，其活度为：

根据谱仪测量可得：

且有：

根据式(6−8)可得活化率方程：

本工作采用的¹⁰³Rh(n,n′)¹⁰³Rh^m反应道，反应产物为¹⁰³Rh^m，ENDF/B-VII.1数据库^[10]提供了其衰变数据，其衰变射线中两条X射线分支比最高，能量（分支比）分别为20.0395keV (2.1043%)和20.1865keV (4.3359%)。这两条X射线能量差别很小，测量时可归并处理。为减少X射线在材料中的自吸收，应采用尽可能薄的样品。实验中使用了厚度为0.025mm的铑金属箔作为活化样品；采用薄窗平面型高纯锗探测器（ORTEC公司生产，型号为：GLP-10180/07-p）测量X射线，以减少探测器外壳和死区对X射线的影响。

根据式(4)计算¹⁰³Rh(n,n′)¹⁰³Rh^m反应的活化率，应首先解决以下三个问题：干扰核素对净全能峰计数的影响、谱仪对源的探测效率确定、以及箔自吸收校正因子的确定。

干扰核素包括两类：一类是其他反应道生成的¹⁰³Rh^m核素；另一类是特征射线与待测射线能量重合的其他活化产生核素。实验所采用的铑金属纯度为99.8%，杂质主要为钌和铱。铱辐照后不产生干扰核素，因此干扰主要来自于钌和铑本身，表 1给出了目标核素和干扰核素的核参数对比。从表 1中可见，干扰主要为第二类，可利用各活化产物半衰期不同的特点，适当选择冷却和测量时间，以避开干扰。

表 1

表 1 目标产物和干扰核素的核参数对比 Table 1 Nuclear parameter of target product vs. interference nuclides. 反应道Reaction path 产物半衰期Product half life 射线分支比Branching ratio / % 103Rh(n,n′)103Rhm 56.1m ~6 103Rh(n,γ)104Rhm 4.34m ~55 103Rh(n,γ)104Rh 42.3s ~0.4 102Ru(n,γ)103Ru 39.4d ~0.7 104Ru(n,γ)105Ru 4.44h ~17

表 1 目标产物和干扰核素的核参数对比 Table 1 Nuclear parameter of target product vs. interference nuclides.

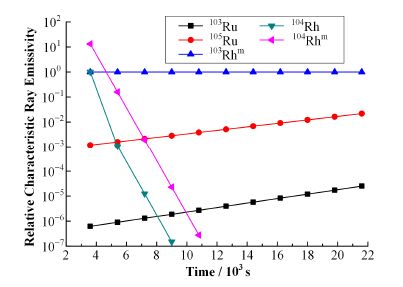
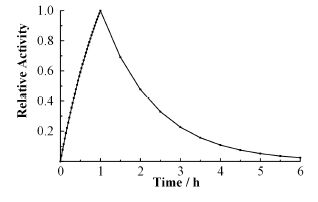
采用ORIGEN2^[11]软件，计算西安脉冲堆典型中子能谱辐照1h后，辐照样品（含0.2%钌的铑金属）中干扰核素的特征射线发射率相对值随时间变化曲线，结果见图 1。计算了¹⁰³Rh^m随时间的活度变化情况，结果见图 2。由图 1可见，¹⁰³Ru和¹⁰⁵Ru的干扰较小，但会随冷却时间而增大，¹⁰⁴Rh和¹⁰⁴Rh^m的干扰较大，随冷却时间延长逐渐降低，其中¹⁰⁴Rh半衰期很短，干扰迅速降低，¹⁰⁴Rh^m的干扰则延续较长，在1.5h处仍超过10%，在2h处降至0.2%左右，基本可以忽略，此时¹⁰³Rh^m仍具有较高活度，约为初始值的50%（图 2），测量窗口可选择在此时开始。测量时间可选择为1h，因为¹⁰³Rh^m半衰期较短，过长的测量时间效用不大，还会受到逐渐升高的¹⁰³Ru和¹⁰⁵Ru干扰影响。

图 1

图 1 干扰核素的特征射线发射率相对值随时间变化曲线 Figure 1 Relative emissivity of characteristic ray of interference nuclides vs. time.

图 2

图 2 103Rhm的活度变化曲线 Figure 2 Activity of 103Rhm vs. time.

实际工作中很难得到20keV左右的校准源进行谱仪效率刻度，且校准源和样品箔的自吸收系数不可能完全一致，即使有合适的校准源，也需要对样品箔的自吸收校正。本文采用了一种结合实验标定和MCNP (Monte Carlo N Particle Transport Code)模拟^[12]计算的混合方法，同时解决了谱仪效率刻度和自吸收校正。

具体方法是利用⁹⁸Mo(n,γ)⁹⁹Mo反应，辐照生产⁹⁹Mo核素，并在放射性平衡后获得⁹⁹Mo-⁹⁹Tc^m平衡体，ENDF/B-VII.1数据库提供了其特征射线和分支比（表 2）。

表 2

表 2 99Mo-99Tcm平衡体核参数 Table 2 Nuclear parameter of 99Mo-99Tcm balanced body. 能量 Energy / keV 分支比Branching ratio / % 18.250 8 3.926 18.367 1 7.483 739.5 12.13

表 2 99Mo-99Tcm平衡体核参数 Table 2 Nuclear parameter of 99Mo-99Tcm balanced body.

⁹⁹Mo-⁹⁹Tc^m平衡体中的干扰核素可忽略不计。实验采用的铑箔纯度可达99.95%，杂质含量极少，成分主要为同族的铬、钨。三种元素原子序数差距大，特征X射线能量差别大，且铬、钨的活化产物无能量在739.5keV附近的特征γ射线。钼元素中只有¹⁰⁰Mo(n,γ)¹⁰¹Mo反应产物的18.35keV特征X射线具有干扰性，但¹⁰¹Mo及其子体¹⁰¹Tc半衰期均只有15min左右，在达到⁹⁹Mo-⁹⁹Tc^m放射性平衡前均已衰变殆尽。

钼箔辐照产生的⁹⁹Mo-⁹⁹Tc^m平衡体，具有与铑箔相近的密度、厚度与特征射线能量，其射线自吸收特征和探测效率与铑箔也接近，其间的较小差别可利用MCNP模拟计算来修正，这样就可将⁹⁹Mo-⁹⁹Tc^m平衡体的活度与铑的活度联系起来，而⁹⁹Mo-⁹⁹Tc^m平衡体具有739.5keV特征γ射线，该射线可以利用良好校准的同轴高纯锗探测器标定测量，得到⁹⁹Mo-⁹⁹Tc^m平衡体的准确活度，从而推算铑的活度。

利用MCNP模拟计算钼、铑箔的探测效率，首先应建立源和探测器模型。探测器的特征尺寸由生产厂商提供参考值，和实际情况有一定差别，且随着探测器使用时间增长，会出现探头晶体部分死层增厚、探测器探测效率降低等情况。因此在建立探测器模型时，应根据校准源校准情况，调节探头晶体的尺寸特征参数，实现计算探测效率与测量探测效率一致。

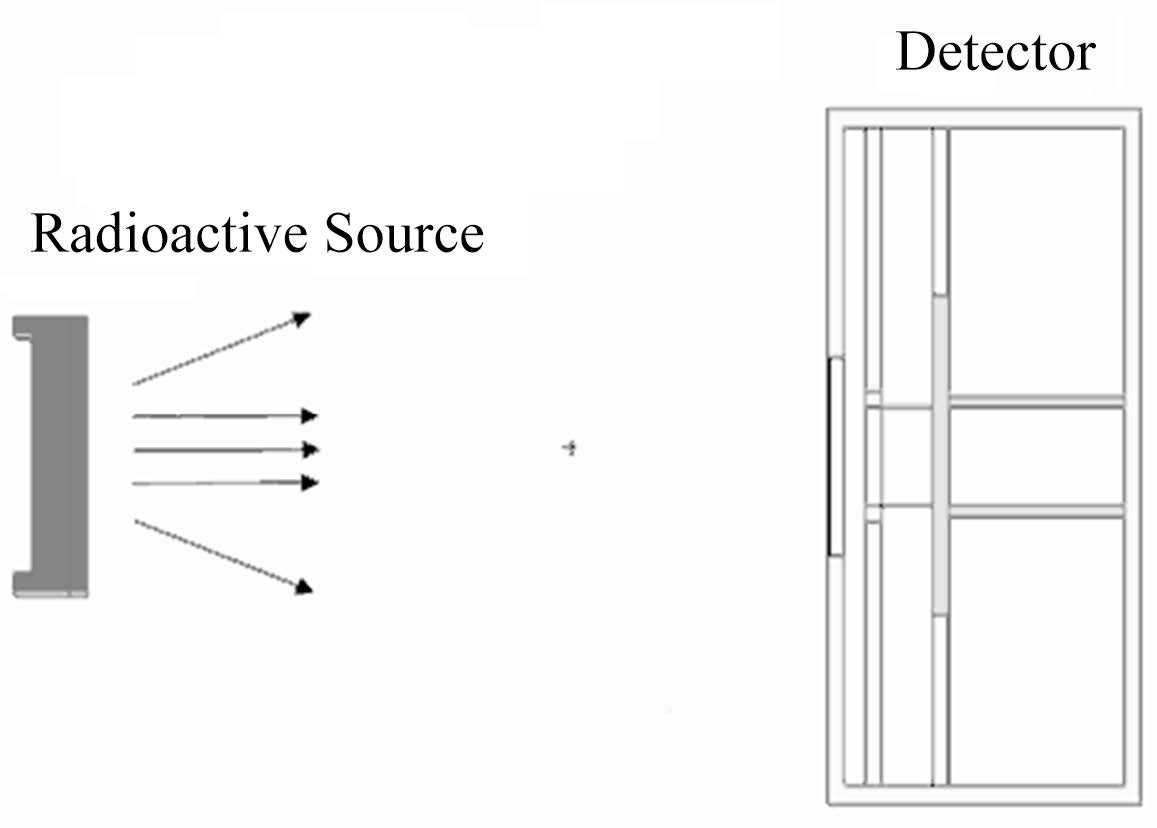
采用¹⁵²Eu源进行探测器校准，该源为直径2.4cm的滤纸源，放置在衬底厚度为0.15cm的扁平有机玻璃源盒内，校准时源盒底部距探测器前表面距离10cm（图 3）。

图 3

图 3 152Eu校准探测器布置 Figure 3 Arrangement of detector calibration with 152Eu

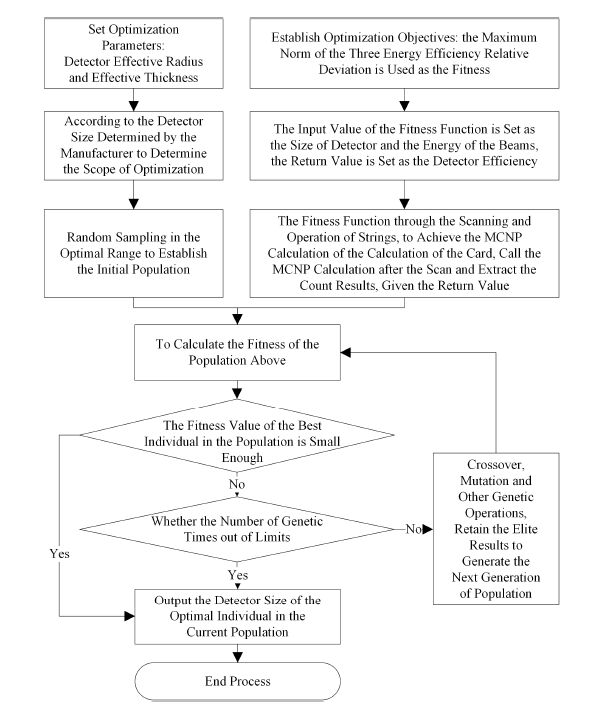
采用厂家给出的参考值建立探测器模型，试算发现不同能量下计算效率均明显大于实验效率（表 3），可能是实际探测器晶体尺寸不准确或死层过大等原因造成的。因此应对晶体的有效半径及有效厚度进行调整，以使计算效率与实验效率统一。利用MATLAB软件提供的遗传算法工具箱编写了基于遗传算法的优化计算程序，该程序可实现自动修改MCNP输入卡片，并调用MCNP程序计算适应度函数；选择探测器晶体有效半径和有效厚度作为优化参数，以三种能量效率相对偏差的最大值范数为适应度，优化计算流程见图 4。最终优化计算结果见表 3，可见优化结果将实验效率和计算效率的相对偏差控制在6%以下。

图 4

图 4 优化计算流程图 Figure 4 Flow chart of optimizing calculation.

表 3

表 3 校准过程实验效率与计算效率的相对偏差 Table 3 Relative deviation of experimental efficiency vs. calculated efficiency in calibration procedure. 能量Energy/ keV 实验效率Experimental efficiency / 10−5 初始计算效率Initial calculation efficiency / 10−5 相对偏差Relative deviation/ % 优化计算效率Optimization calculation efficiency / 10−5 相对偏差Relative deviation/ % 121.78 18.48 28.23 52.8 17.45 −5.57 244.7 3.428 6.068 77 3.621 5.63 344.28 1.488 2.542 70.8 1.45 −2.55

表 3 校准过程实验效率与计算效率的相对偏差 Table 3 Relative deviation of experimental efficiency vs. calculated efficiency in calibration procedure.

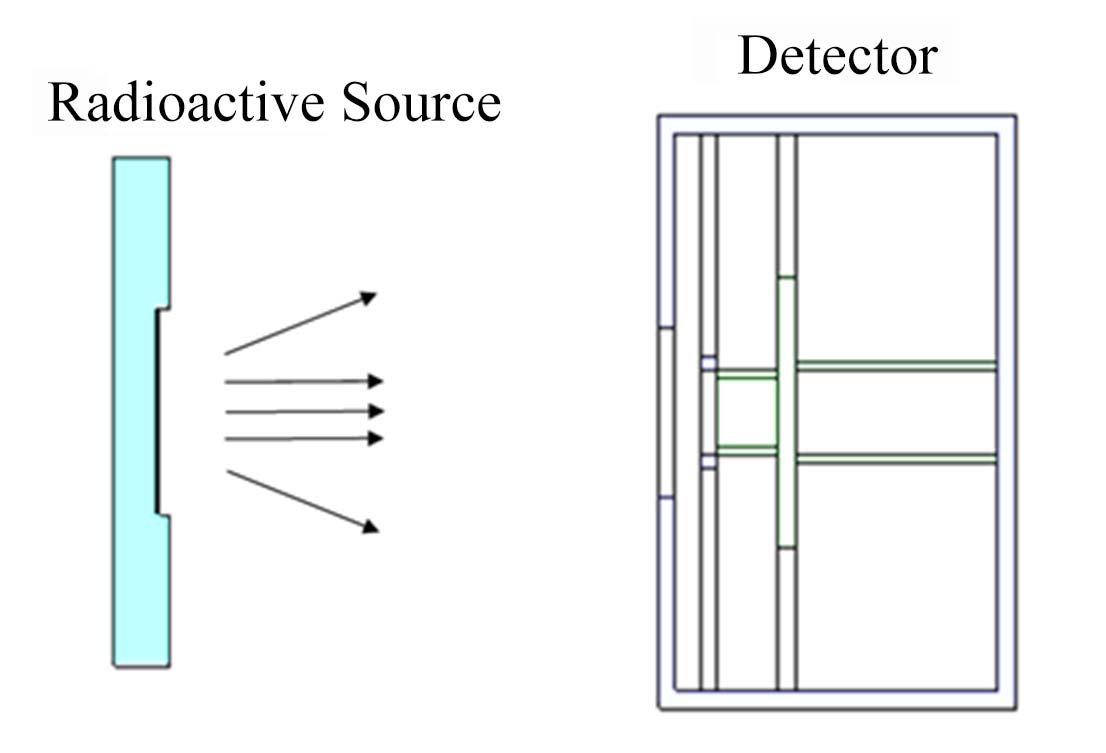
利用优化后的探测器晶体特征参数，针对实际实验条件，建立铑、钼箔活度测量的MCNP模型（图 5）。两活化箔厚度相同，均为0.025mm；为了使钼箔便于装入源盒，二者直径稍有差异，铑箔直径为24mm，钼箔直径为20mm，在同轴探测器上标定；用双面胶将活化箔固定在有机玻璃源架上，保证其正面无遮挡；两活化箔距离探测器前表面均为5.2cm，利用计算效率的比例关系（式(10)），就可以根据钼已知的实验探测效率推导出铑的实验探测效率，结果见表 4。

图 5

图 5 铑箔和钼箔的测量布置 Figure 5 Arrangement of measurements of Rh foil and Mo foil.

表 4

表 4 测量过程中实验效率与计算效率的相对偏差 Table 4 Relative deviation of experimental efficiency vs. calculated efficiency in measurements. 活化箔Activation foil 特征X射线能量Characteristic X-ray energy / keV 实验效率Experimental efficiency/ 10−4 计算效率Calculation efficiency/ 10−4 钼Mo 18.2508/18.3671 8.239 8.852 铑Rh 20.0395/20.1865 7.661 8.231

表 4 测量过程中实验效率与计算效率的相对偏差 Table 4 Relative deviation of experimental efficiency vs. calculated efficiency in measurements.

式中：ε_e,Rh、ε_c,Rh为铑箔特征X射线的实验效率和计算效率；ε_e,Mo、ε_c,Mo为钼箔特征X射线的实验效率和计算效率。

对西安脉冲堆某次辐照实验进行了0.1MeV以上快中子注量测量，并与铁、硫、镍等活化箔测量数据进行了比较，结果见表 5。

表 5

表 5 4种活化箔的快中子注量测量值比较 Table 5 Measurement of fast neutron fluence of four activation foils. 活化反应道Activation reaction channel 谱平均截面Average cross section / b 活化率Activation rate / 10−15 快中子注量测量值Measured value of fast neutron fluence (>0.1 MeV) / 1014 n·cm−2 54Fe(n,p)54Mn 0.027 6 1.38 1.8 32S(n,p)32P 0.024 9 1.12 1.62 58Ni(n,p)58Co 0.039 6 1.81 1.65 103Rh(n,n′)103Rhm 0.463 4 23.2 1.8

表 5 4种活化箔的快中子注量测量值比较 Table 5 Measurement of fast neutron fluence of four activation foils.

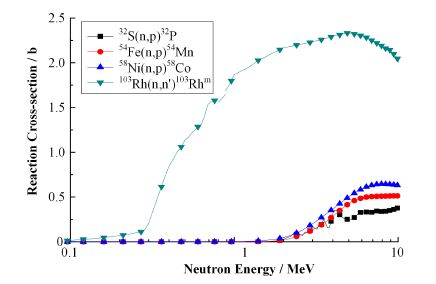
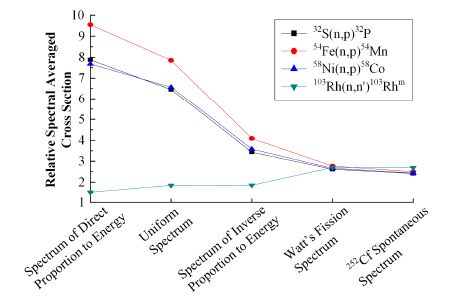
表 5中铑箔测量数据与其他几种核素的符合性较好。应用铑箔的优势主要在于其较宽的中子灵敏范围。图 6给出了几种活化反应的截面，由于¹⁰³Rh(n,n′)¹⁰³Rh^m反应截面最大，且中子敏感能区下限低至0.1MeV，中子能谱灵敏范围高于其他几种快中子探测箔，这就造成其谱平均截面对中子能谱的敏感性相对较低。图 7计算了5种中子能谱条件下，4种活化反应谱平均截面相对于西安脉冲堆辐照腔实验装置谱平均截面的变化，从图 7中可见，¹⁰³Rh(n,n′)¹⁰³Rh^m反应的谱平均截面稳定性最好。因此在中子能谱未知的情况下进行快中子注量测量，利用¹⁰³Rh(n,n′)¹⁰³Rh^m反应测得的数据会更可信。

图 6

图 6 4种活化反应的截面 Figure 6 Cross section of four activation reactions.

图 7

图 7 不同能谱条件下几种活化反应截面的相对变化 Figure 7 Relative variety of cross section of several activation reactions with different neutron spectra.

对以上西安脉冲堆某次辐照实验的快中子注量¹⁰³Rh(n,n′)¹⁰³Rh^m测量结果进行不确定度分析。

由式(1)可知，${\phi _{{E_0}}}$的合成不确定度可表示为：

为活化率不确定度，其不确定度的主要分量来源为c、γ_d、ε、λ，各项分量相关性可忽略，不确定度可表示为式(12)：

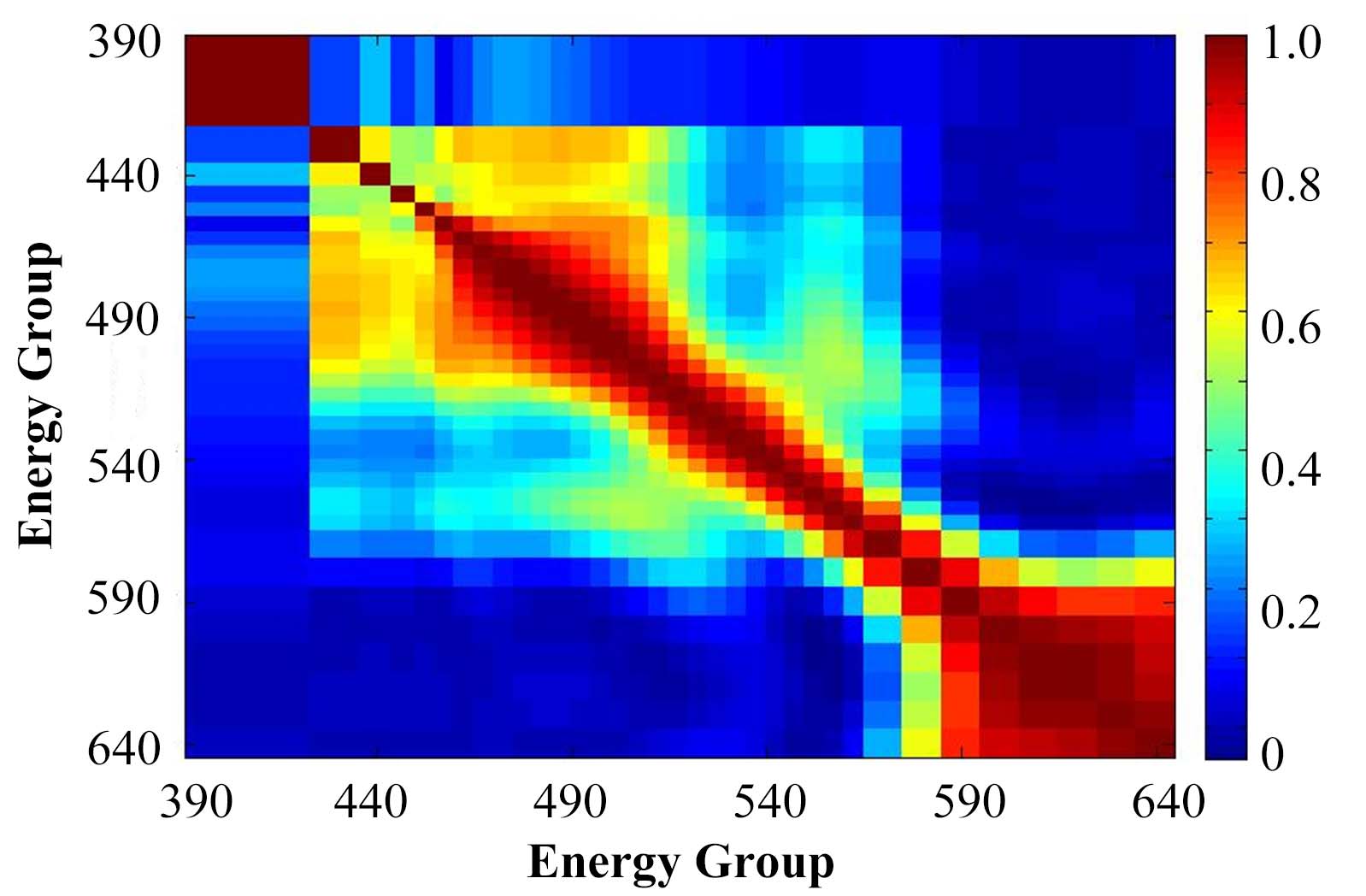
为谱平均截面不确定度，各能群截面之间的相关性由核数据库的协方差数据（图 8）给出，则其不确定度公式可表示为式(13)：

$u({t_r})/{t_r}$为辐照时间不确定度。主要由反应堆启停时间手工折算引入，实验中采用了计算机连续采集反应堆功率数据，最后积分折算的方法，基本消除了手动折算引入的误差，故此分项可忽略。

表 6给出了各分量值和合成不确定度评定结果，可见¹⁰³Rh(n,n′)¹⁰³Rh^m反应测量快中子注量合成不确定度约为13.1%。采用相同方法，对其他三种反应也进行了不确定度分析，结果列于表 7。表 7中值相对于文献值偏大，ASTM标准^[3-5]根据标准裂变场下的测量数据，对硫、铁、镍三种活化箔作中子注量相对测量时的不确定度给出的评价值均在5%以下。该评价值较小的原因是标准只计入了A类（即表 6中的净全能峰计数的不确定度，为1.77%）随机不确定度和B类（即表 6中谱仪对源的探测效率不确定度，为5.63%）中的探测效率误差，未定量考虑能谱不确定度和谱平均截面不确定度，仅考虑这两项因素的话，则测量不确定度为5.90%。

表 6

表 6 103Rh(n,n′)103Rhm反应测量快中子注量的不确定度分析 Table 6 Uncertainty analysis of fast neutron fluence measurement with 103Rh(n,n′)103Rhm reaction. 分量Component 不确定度来源Uncertainty source 合成值Synthetic value 活化率不确定度Uncertainty of activation rate 净全能峰计数Net almighty count 0.0177 0.125 特征射线分支比Characteristic ray branching ratio 0.11 谱仪对源的探测效率Detection efficiency of the spectrometer to the source 0.0563 产生核素的衰变常数Decay constant of a generation 0.035 6% 谱平均截面不确定度Spectral mean cross section uncertainty 群截面不确定度Group cross section uncertainty ENDF/B-VII 0.0387 能谱不确定度Energy spectrum uncertainty 0.2 快中子注量不确定度Uncertainty of fast neutron flux 0.131

表 6 103Rh(n,n′)103Rhm反应测量快中子注量的不确定度分析 Table 6 Uncertainty analysis of fast neutron fluence measurement with 103Rh(n,n′)103Rhm reaction.

表 7

表 7 4 种活化箔的快中子注量测量不确定度 Table 7 Measurement uncertainty of fast neutron fluence of four activation foils. 活化反应道Activation reaction channel 活化率不确定度Uncertainty of activation rate / % 谱平均截面不确定度Spectral mean cross section uncertainty / % 快中子注量测量不确定度Uncertainty of fast neutron flux measurement / % 54Fe(n,p)54Mn 3.61 3.46 5.04 32S(n,p)32P 8.06 3.32 8.72 58Ni(n,p)58Co 3.16 2.75 4.19 103Rh(n,n′)103Rhm 12.5 3.87 13.1

表 7 4 种活化箔的快中子注量测量不确定度 Table 7 Measurement uncertainty of fast neutron fluence of four activation foils.

表 7中¹⁰³Rh(n,n′)¹⁰³Rh^m反应测量快中子注量不确定度最大，其原因主要来源于特征射线分支比。因为¹⁰³Rh^m的特征射线为X射线，其分支比不确定度较大，核数据库评价值为10%，大大高于一般放射性核素γ射线分支比的不确定度，如⁵⁴Mn、³²P、⁵⁸Co特征射线分支比不确定度均小于1‰。这是¹⁰³Rh(n,n′)¹⁰³Rh^m反应作快中子注量监测用的主要缺陷。下一步工作可以考虑利用铁和铑活化箔同时在标准中子场中辐照，利用铁的测量数据修正该特征射线分支比，以降低不确定度。

图 8

图 8 103Rh(n,n′)103Rhm反应截面相关系数 Figure 8 Correlation coefficient of 103Rh(n,n′)103Rhm reaction.

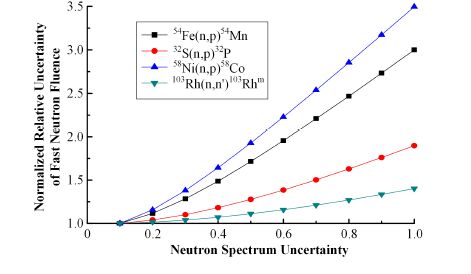
对4种反应测量的快中子注量不确定度相对于能谱不确定度进行敏感性分析，见图 9。从图 9中可见¹⁰³Rh(n,n′)¹⁰³Rh^m测量快中子注量不确定度相对于能谱不确定度的敏感性最低，随着能谱不确定度的增大，变化较为缓慢；³²S(n,p)³²P反应敏感性稍高，⁵⁴Fe(n,p)⁵⁴Mn和⁵⁸Ni(n,p)⁵⁸Co反应敏感性最强。这也表明了在能谱不确定度很大的条件下，¹⁰³Rh(n,n′)¹⁰³Rh^m反应作快中子注量监测时具有 优势。

图 9

图 9 快中子注量测量不确定度随能谱不确定度的变化 Figure 9 Measurement uncertainty of fast neutron fluence vs. neutron spectrum uncertainty.

本文应用一种混合标定方法，实现了¹⁰³Rh^m活化率的准确测量，从而建立了基于¹⁰³Rh(n,n′)¹⁰³Rh^m反应监测快中子注量的方法。与铁、镍、硫等活化箔开展实验对比，并进行了不确定度分析。结果显示，该方法测量西安脉冲堆辐照实验装置内的快中子注量不确定度约为13.1%，相对于其他活化箔偏大，但其具有能量覆盖范围广、能谱变化敏感性低的优点。在中子能谱未知的情况下进行快中子注量测量，该方法具有一定的优势。