2. 兰州大学 教育部中子应用技术工程研究中心 兰州 730000
2. Engineering Research Center for Neutron Application, Ministry of Education, Lanzhou University, Lanzhou 730000, China
紧凑型D-D中子发生器是一种可产生约2.5MeV快中子的小型化加速器单能快中子源,与D-T中子发生器相比,不使用放射性氚靶,更具安全性,且存在氘离子自注入效应、靶寿命长、运行成本低、可代替同位素中子源等优点,在工业在线中子活化分析、中子照相、爆炸物及毒品检测等方面有广泛的应用价值[1-2]。早先的紧凑型D-D中子发生器主要以密封中子管为主,密封中子管的优点是尺寸很小,其缺点是使用微型潘宁离子源,D束流只有几十微安,D-D中子产额低,且是一次性真空密封设备,寿命偏短,使用成本高。开发D束流大于1 mA,D-D中子产额大于108 n∙s-1,元件可更换的紧凑型长寿命D-D中子发生器已成为中子应用技术开发的迫切需要。国际上一些重要实验室已发展了各种形式的紧凑型中子发生器[3-5],国内此方面的研究相对滞后[6-7]。
在兰州大学,一台紧凑型D-D中子发生器正在研制中。其中,紧凑型D-D中子发生器的快中子产额的准确测量是需解决的关键问题。伴随粒子法是实现D-D中子发生器快中子产额绝对测量的手段之一,在低能D束下,D-D聚变反应存在以下两个反应道:D(d,n)3He反应和D(d,p)T反应。其中,第一个反应道产生快中子n和伴随粒子3He,第二个反应道产生质子(p)和氚(T)粒子,因3He能量偏低(约0.78 MeV),难于准确测量,一般通过测量第二个反应道产生的能量较高的伴随质子(能量约3.05 MeV)来实现D-D中子产额测量[8]。
在采用伴随质子法实现D-D中子产额测量中,有两个参数需要通过理论计算来确定,即中子和质子的产额比和出射中子的各向异性修正因子。早先的工作大多针对135伴随粒子法开展了修正因子计算[9-11],90伴随粒子法的相关研究较少,而且早先的工作采用了较早的D-D反应截面数据,计算结果存在较大的不确定度。本文针对紧凑型D-D中子发生器90伴随粒子法中子产额测量的需求,开展相关理论研究和修正因子计算方法研究,计算给出入射氘离子能量在20-700 keV范围,90伴随粒子法D-D中子产额测量所需修正因子数据,为紧凑型D-D中子发生器中子产额的测量提供基础数据。数据也可用于其他类型D-D中子发生器伴随粒子法D-D中子产额测量。
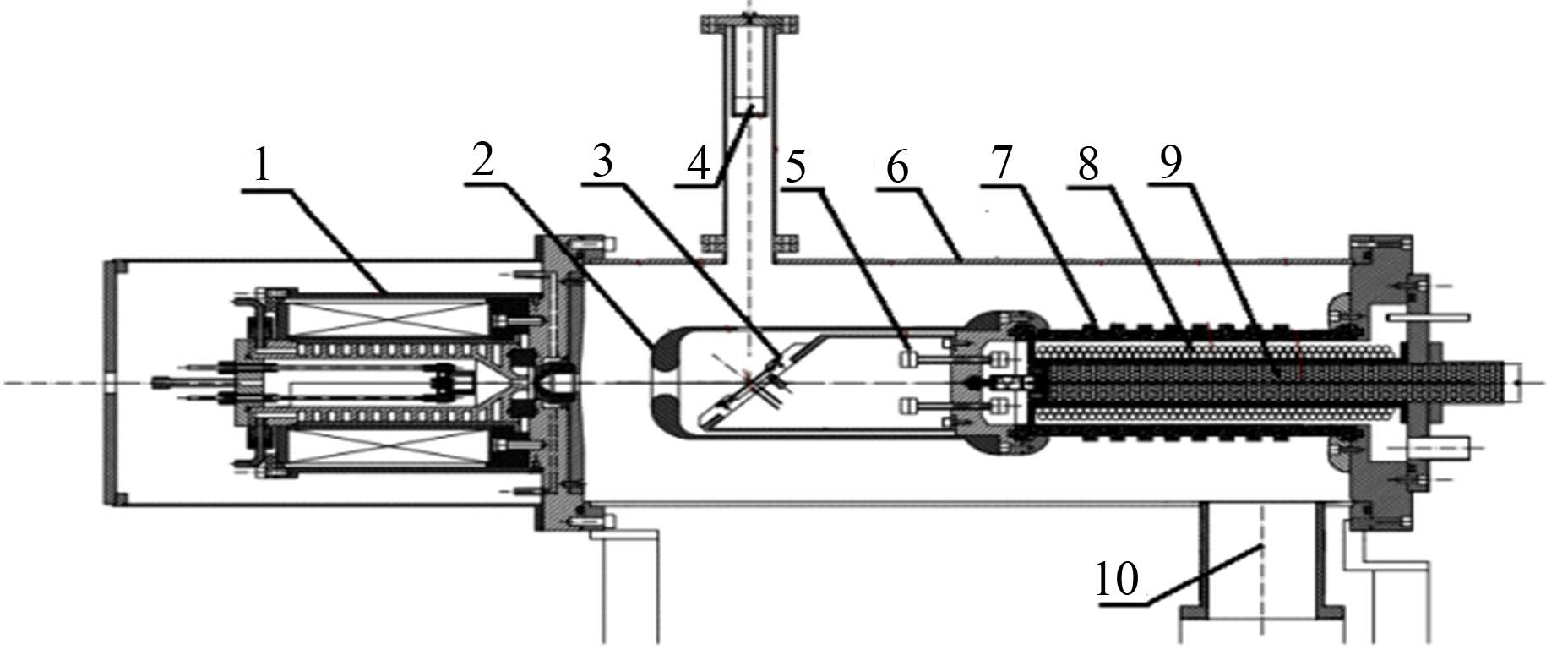
1 紧凑型D-D中子发生器结构及90伴随粒子法中子产额测量原理如图 1所示,紧凑型D-D中子发生器由离子源、离子束引出加速系统、靶系统、高压接头、真空腔和真空泵等部分装配而成。离子束引出加速系统可将离子源引出D离子加速到100-120 keV,轰击在D靶上,发生D-D聚变反应,产生能量约2.5 MeV的快中子。中子发生器结构为圆筒形,长约98 cm,最大法兰外径为28 cm。在90方向有一管道用于安装金硅面垒探测器,通过测量D-D反应产生的伴随质子来实现D-D中子产额测量。
|
图 1 紧凑型高产额D-D中子发生器结构示意图 1. 离子源,2. 引出加速电极,3. 靶,4. 金硅面垒探测器,5. 靶冷却管道接头,6. 不锈钢外壳,7. 绝缘环,8. 冷却管道,9. 高压电缆,10. 真空抽气口 Figure 1 Schematic of compact high-yield D-D neutron generator. 1. Ion source,2. Accelerating electrode,3. Target,4. Au-Si surface barrier detector,5. Cooling joints of target,6. Stainless steel shell,7. Insulating ring,8. Cooling duct,9. High voltage cables,10. Vacuum suction |
在厚靶条件下,D-D中子产额可用式(1)描述[8]:
| ${{Y}_{n}}=4\pi \frac{{{n}_{p}}}{{{\Omega }_{p}}}{{R}_{thick}}{{\left( \frac{{{Y}_{d,n}}}{{{Y}_{d,p}}} \right)}_{thick}}$ | (1) |
式中:np为探测器测到的伴随质子计数率;Ωp为探测器对靶点所张立体角;Rthick为各向异性修正因子;(Yd,n/Yd,p)为D-D反应中子与质子的积分产额比。各向异性修正因子和中子与质子的积分产额比可分别由式(2)、(3)描述[9-10],即:
| ${{R}_{thick}}=\frac{\int\limits_{0}^{{{E}_{d}}}{\left( {\frac{{{\sigma }_{d,p}}\left( E \right)}{4\pi }}/{\frac{dE}{dx}\left( E \right)}\; \right)dE}}{\int\limits_{0}^{{{E}_{d}}}{\left( {\frac{d{{\sigma }_{d,p}}}{d\omega '}\left( E,\theta \right)}/{\frac{dE}{dx}\left( E \right)}\; \right)\left( \frac{d\omega '}{d\omega }\left( E,\theta \right) \right)dE}}$ | (2) |
| ${{\left( \frac{{{Y}_{d,n}}}{{{Y}_{d,p}}} \right)}_{thick}}=\frac{\int_{0}^{{{E}_{d}}}{\left( {\frac{{{\sigma }_{d,n}}\left( E \right)}{4\pi }}/{\frac{dE}{dx}\left( E \right)}\; \right)dE}}{\int_{0}^{{{E}_{d}}}{\left( {\frac{{{\sigma }_{d,p}}\left( E \right)}{4\pi }}/{\frac{dE}{dx}\left( E \right)}\; \right)dE}}$ | (3) |
式中:Ed为入射氘束能量;σd,n(E)和σd,p(E)分别为实验室系中D(d,n)3He和D(d,p)T反应的积分截面;(dσd,p/dω')(E,θ)为质心系中D(d,p)T反应对应实验室系θ方向出射质子的微分截面;(dE/dx)(E)为氘离子在氘钛(DTi)靶中的阻止本领;(dω'/dω)(E,θ)为质心系和实验室系之间的立体角转换因子。
综上所述,将Rthick和(Yd,n/Yd,p)thick的乘积记为总的修正因子RY,即:
| ${{R}_{Y}}={{R}_{thick}}{{\left( \frac{{{Y}_{d,n}}}{{{Y}_{d,p}}} \right)}_{thick}}$ | (4) |
则D-D反应的中子产额可表达为:
| ${{Y}_{n}}=4\pi \frac{{{n}_{p}}}{{{\Omega }_{p}}}{{R}_{Y}}$ | (5) |
由式(5)可见,要实现伴随粒子法D-D反应中子产额的绝对测量,必须根据D-D反应截面数据计算出各向异性修正因子及中子与质子的积分产额比。
2 计算方法针对紧凑型D-D中子发生器90伴随粒子法中子产额测量,本研究将采用薄靶近似方法计算各向异性修正因子和中子与质子的积分产额比,即将厚靶分割成很多足够薄的薄层,每一薄层可被近似看作一个薄靶,则由式(2)、(3),各向异性修正因子和中子与质子的积分产额比可近似转化为下列求和形式,即:
| ${{R}_{thick}}=\frac{\sum\limits_{i}{\left( {\frac{{{\sigma }_{d,n}}\left( {{E}_{i}} \right)}{4\pi }}/{\frac{dE}{dx}\left( {{E}_{i}} \right)}\; \right)\Delta {{E}_{i}}}}{\sum\limits_{i}{\left( {\frac{d{{\sigma }_{d,p}}}{d\omega '}\left( {{E}_{i}},\theta \right)}/{\frac{dE}{dx}\left( {{E}_{i}} \right)}\; \right)\left( \frac{d\omega '}{d\omega }\left( {{E}_{i}},\theta \right) \right)\Delta {{E}_{i}}}}$ | (6) |
| ${{\left( \frac{{{Y}_{d,n}}}{{{Y}_{d,p}}} \right)}_{thick}}=\frac{\sum\limits_{i}{\left( {\frac{{{\sigma }_{d,n}}\left( {{E}_{i}} \right)}{4\pi }}/{\frac{dE}{dx}\left( {{E}_{i}} \right)}\; \right)\Delta {{E}_{i}}}}{\sum\limits_{i}{\left( {\frac{d{{\sigma }_{d,p}}}{4\pi }\left( {{E}_{i}} \right)}/{\frac{dE}{dx}\left( {{E}_{i}} \right)}\; \right)\Delta {{E}_{i}}}}$ | (7) |
式中:Ei为氘束入射到第i层时的能量;ΔEi为氘离子在第i层中损失的能量。设E0=Ed,ΔEi=0,Ei和ΔEi可由式(8)、(9)计算,即:
| ${{E}_{i}}={{E}_{i-1}}-\Delta {{E}_{i-1}}$ | (8) |
| $\Delta {{E}_{i-1}}=\frac{dE}{dx}\left( {{E}_{i-1}} \right)\Delta {{x}_{i-1}}$ | (9) |
式中:Δxi-1为被分割的靶中第i-1薄层厚度。
立体角转化因子
| $\frac{d\omega '}{d\omega }\left( {{E}_{i}},\theta \right)=\frac{J{{\left\{ \cos \theta +{{\left[ \left( {\left( {{J}^{2}}+L \right)}/{{{J}^{2}}}\; \right)-{{\sin }^{2}}\theta \right]}^{\frac{1}{2}}} \right\}}^{2}}}{{{\left( E_{ip}^{'} \right)}^{\frac{1}{2}}}{{\left[ \left( {\left( {{J}^{2}}+L \right)}/{{{J}^{2}}}\; \right)-{{\sin }^{2}}\theta \right]}^{\frac{1}{2}}}}$ | (10) |
| $J=\frac{{{\left( {{m}_{1}}{{m}_{3}}{{E}_{i}} \right)}^{\frac{1}{2}}}}{{{m}_{3}}+{{m}_{4}}}$ | (11) |
| $L=\frac{{{m}_{4}}\left( Q+{{E}_{i}} \right)-{{m}_{1}}{{E}_{i}}}{{{m}_{3}}+{{m}_{4}}}$ | (12) |
式中:m1、m2、m3、m4分别为射氘离子、靶核氘、出射质子和氚的质量;Q为D(d,p)T反应的反应能(Q=4.033 MeV);E'ip为质心系中的质子能量,可由式(13)-(15)计算[12]:
| $E_{ip}^{'}={{E}_{ip}}\times {{\left( \frac{\sin \theta }{\sin {{\theta }_{c}}} \right)}^{2}}$ | (13) |
| ${{\theta }_{c}}=\theta +{{\sin }^{-1}}\left( \gamma \sin \theta \right)$ | (14) |
| $\gamma ={{\left( \frac{{{E}_{i}}}{3\left( {{E}_{i}}+2Q \right)} \right)}^{\frac{1}{2}}}$ | (15) |
式中:θ=90为实验室系中质子出射角;θc为质心系中质子出射角;Ei为入射氘离子能量;Eip为实验室系中θ方向的质子能量,可由式(16)给出[13]:
| $E_{ip}^{'}=\left[ \begin{align} & 0.35402{{E}_{i}}^{{}^{1}\!\!\diagup\!\!{}_{2}\;}\cos \theta \\ & +\frac{{{\left( 2.0382{{E}_{i}}{{\cos }^{2}}\theta +48.92325+4.03062{{E}_{i}} \right)}^{{}^{1}\!\!\diagup\!\!{}_{2}\;}}}{4.02276} \\ \end{align} \right]$ | (16) |
质心系中,(dσd,p/dω')(Ei,θ)为D(d,p)T反应对应实验室系θ方向出射质子的微分截面,可根据式(17)、(18)进行计算[14-15],即:
| $\frac{d{{\sigma }_{d,p}}}{d\omega '}\left( {{E}_{i}},\theta \right)=a+b{{\cos }^{2}}{{\theta }_{c}}+c{{\cos }^{4}}{{\theta }_{c}}\left( {{E}_{i}}\le 110ke\text{V} \right)$ | (17) |
| $\frac{d{{\sigma }_{d,p}}}{d\omega '}\left( {{E}_{i}},\theta \right)=\frac{d{{\sigma }_{d,p}}\left( {{90}^{0}} \right)}{d\omega '}\left[ \begin{align} & 1+A{{\cos }^{2}}\left( {{\theta }_{c}} \right)+ \\ & B{{\cos }^{4}}\left( {{\theta }_{c}} \right) \\ \end{align} \right]\left( {{E}_{i}}>110ke\text{V} \right)$ | (18) |
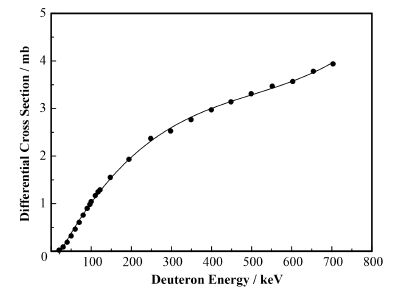
式中:a、b、c和A、B为常数;dσd,p(90)/dω'为质心系中θc=90的D(d,p)T反应微分截面,常数和质心系微分截面数据见文献[14-15]。质心系下(dσd,p/dω')(Ei,θ)的计算结果如图 2所示。
|
图 2 质心系下D(d,p)T反应对应实验室系θ=90方向出射质子的微分截面 Figure 2 Differential cross sections for D(d,p)T in the centroid system corresponding to the laboratory system for the proton at θ=90. |
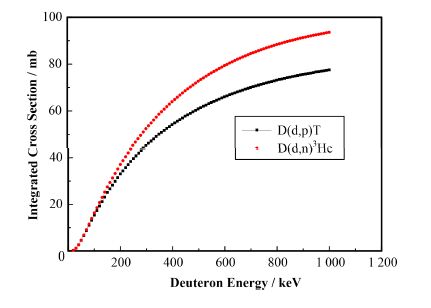
实验室系D(d,n)3He和D(d,p)T反应的积分截面σd,p和σd,n采用了ENDF-B-VI库的推荐数据,如图 3所示;式(6)、(7)所需的阻止本领数据由SRIM-2008程序计算给出[16]。
|
图 3 实验室系D(d,n)3He和D(d,p)T反应积分截面 Figure 3 Integral reaction cross section of D(d,n)3He and D(d,p)T in the laboratory system. |
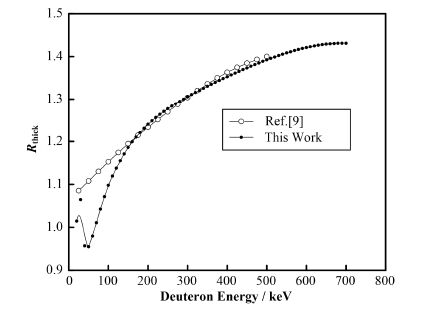
根据上述计算方法及相关数据,利用MATLAB软件平台,开发了一个计算程序。应用所开发的程序,完成了入射氘束能量20-00 keV范围,90伴随粒子法D-D中子产额测量所需的各向异性修正因子、中子和质子产额比、总修正因子的理论计算,并将计算结果同早先Ruby的研究数据[9]进行了比较,结果分别如图 4-6所示。
|
图 4 各向异性因子Rthick计算结果与文献[9]数据对比 Figure 4 Result of anisotropy factor Rthick and the comparison with the Ref.[9] data. |
|
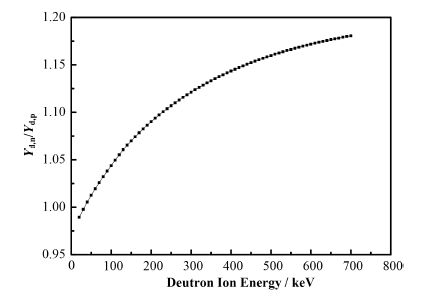
图 5 D(d,n)3He反应中子和D(d,p)T反应质子积分产额比 Figure 5 Yield ratio of the neutron for D(d,n)3He and the proton for D(d,p)T. |
|
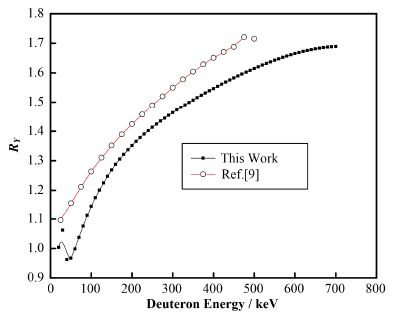
图 6 总修正异性因子RY计算结果与文献[9]数据对比 Figure 6 Result of total correction factor RY and the comparison with the Ref.[9] data. |
由图 4可以看出,D束能量在100-500 keV能区,本研究计算给出的各向异性修正因子Rthick结果与Ruby的数据[9]一致性较好,相对偏差小于0.8%;在D束流能量50 keV附近,两者之间差异最大,最大偏差为13.6%(对应D能量50 keV),这可能与Ruby使用了较早的截面数据有关。
由图 5可以看出,在D束能量小于50 keV能区,中子和质子产额比小于1.0;在D束能量大于50 keV能区,中子和质子产额比大于1.0,并随D束流能量而增大,这一特征是由图 3所示ENDF-B-VI库给出的D(d,n)3He和D(d,p)T反应积分截面新数据所导致,也是造成本研究计算给出的Rthick与Ruby给出的结果[9](Ruby使用了较早的反应截面数据)在D束能量50 keV附近存在较大差异的原因。
由图 6可以看出,在D束能量50 keV能区附近,总修正因子RY的计算结果和Ruby给出的数据[9]之间也存在较大差异,最大偏差为16.2%;在D束能量200 keV 附近,差异较小,两者之间的相对偏差约为4%,随后随着D束能量的增大,相对偏差逐渐增大,到500 keV附近,相对偏差约6%。上述偏差也与Ruby使用了较早的截面数据有关。
4 结语对90伴随粒子法D-D中子产额测量中的修正因子计算方法进行了研究,基于MATLAB软件平台,开发了用于修正因子计算的计算机程序,计算给出了厚靶条件下,入射氘能量在20-00 keV范围,90伴随粒子法D-D中子产额测量各向异性修正因子Rthick、中子和质子产额比(Yd,n/Yd,p)thick及总修正因子RY,并与早先的研究结果进行了对比分析。
就本工作的计算方法,只要厚靶被分割得足够薄,薄靶近似所带来的不确定度很小,可忽略。修正因子计算数据的不确定度主要来自于D离子在靶中的阻止本领数据和D-D反应截面数据。其中,阻止本领计算的不确定度约为5%,由式(6)、(7)可以看出,方程中分子分母均包含阻止本领项,阻止本领数据的不确定度相互抵消,故此项所带来的不确定度也可以忽略不计;ENDF-B-VI库给出的D(d,n)3He和D(d,p)T反应积分截面数据和文献[14-15]给出的微分截面数据的不确定度约为2%,故修正因子计算数据的不确定度约为2%。
| [1] |
魏国海, 韩松柏, 陈东风, 等. 中子照相技术在核燃料元件无损检测中的应用[J].
核技术
, 2012, 35(11): 821–826.
WEI Guohai, HAN Songbai, CHEN Dongfeng, et al. Application of neutron radiography for non-destructive testing nuclear fuel elements[J]. Nuclear Techniques, 2012, 35(11): 821–826. |
| [2] |
袁国军, 肖才锦, 金象春, 等. 北京市场10种膳食鱼微量元素的中子活化分析[J].
核技术
, 2013, 36(9): 090207.
YUAN Guojun, XIAO Caijin, JIN Xiangchun, et al. Study on trace elements of ten kinds of fish species at Beijing market by INAA[J]. Nuclear Techniques, 2013, 36(9): 090207. DOI: 10.11889/j.0253-3219.2013.hjs.36.090207 |
| [3] | Reijonen J, Gicquel F, Leung K N, et al. D-D neutron generator development at LBNL[J]. Applied Radiation and Isotopes, 2005, 63: 757–763. DOI: 10.1016/j.apradiso.2005.05.024 |
| [4] | Ludewigt B A, Wells R P, Reijonen J. High-yield D-T neutron generator[J]. Nuclear Instruments and Methods in Physics Research B, 2007, 261: 830–834. DOI: 10.1016/j.nimb.2007.04.246 |
| [5] | Reijonen J. Neutron generators developed at LBNL for homeland security and imaging applications[J]. Nuclear Instruments and Methods in Physics Research B, 2007, 261: 272–276. DOI: 10.1016/j.nimb.2007.04.192 |
| [6] |
张国光, 沈冠仁, 丰树强, 等. 小型化中子发生器研制进展[J].
中国原子能科学研究院年报
, 2012(1): 344–346.
ZHANG Guoguang, SHEN Guanren, FENG Shuqiang, et al. The development of miniaturized neutron generator[J]. China Institute of Atomic Energy Annual Report, 2012(1): 344–346. |
| [7] |
肖坤祥, 冉汉正, 曾清, 等. 高产额中子发生器研制[J].
原子能科学技术
, 2012, 46(B09): 713–717.
XIAO Kunxiang, RAN Hanzheng, ZENG Qing, et al. Development of high-yielding neutron generator[J]. Atomic Energy Science and Technology, 2012, 46(B09): 713–717. |
| [8] | Yan Y, Lu X L, Yao Z E, et al. Study on the method with associated particle for measuring the neutron yield of D-D neutron generator[J]. Nuclear Instruments and Methods in Physics Research A, 2015, 773: 52–55. DOI: 10.1016/j.nima.2014.11.023 |
| [9] | Ruby L, Crawford R B. Anisotropy factors for determination of total neutron yield from the D (d, n)3He and T (d, n)4He reactions[J]. Nuclear Instruments and Methods, 1963, 24: 413–417. DOI: 10.1016/0029-554X(63)90358-6 |
| [10] | Jordanova J. Anisotropy factors for determination of neutron yield from the 2H (d, n)3He and T (d, n)4He reaction[J]. Journal of Radio Analytical and Nuclear Chemistry, 1995, 200: 127–135. DOI: 10.1007/BF02163682 |
| [11] |
中国原子能科学研究院.
加速器单能中子源常用数据手册[M]. 北京: 科学出版社, 1976: 215-217.
China Institute of Atomic Energy. Accelerator monoenergetic neutron source common data manual[M]. Beijing: Science Press, 1976: 215-217. |
| [12] |
卢希庭.
原子核物理[M]. 北京: 原子能出版社, 2000: 235-236.
LU Xiting. Nuclear physics[M]. Beijing: Atomic Energy Press, 2000: 235-236. |
| [13] | Csikai G J. CRC handbook of fast neutron generators[M]. 1987. |
| [14] | Brown R E, Jarmie N. Differential cross sections at low energies for 2H (d, p)3H and 2H (d, n)3He[J]. Physical Review C, 1990, 41(4): 1391–1400. DOI: 10.1103/PhysRevC.41.1391 |
| [15] | Theus R B, McCarry W I, Beach L A. Angular distributions and cross-section ratios for the reactions 2H (d, n)3He and 2H (d, p)3H below 500 keV[J]. Nuclear Physics, 1966, 80: 273–288. DOI: 10.1016/0029-5582(66)90089-7 |
| [16] | James F Z. Beam interactions with materials and atoms[J]. Nuclear Instruments and Methods in Physics Research B, 2004, 219: 1027–1036. |


