2. 中国科学院大学 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
束流诊断系统是加速器调试、研究和性能提升必不可少的关键系统,作为自由电子激光装置调试和运行时的主要工具,具备测量电子束流各项参数的基本功能。束流诊断系统是随着加速器技术的发展同步发展的,为满足加速器运行和物理研究的需要,束流诊断系统也越来越复杂,在加速器束流注入、调整、运行以及研究过程中的作用也愈加重要,通过对束流和加速器参数的测量,可以优化机器参数、改善束流品质和提升实验效率。
束团长度是电子束最重要的纵向参数之一,是反映束流纵向不稳定性发生的阈值和不稳定强度的主要参数,它将直接影响物理实验的效率。束团长度的测量对于优化加速器参数至关重要。首先,束团长度测量可以为加速器中束流产生理论模型提供实验验证;其次,束团长度测量有助于我们理解在产生超短电子束团过程中的一些非线性效应,进而为产生更短的电子束团提供基础,比如对磁压缩过程的研究;最后,在利用超短电子束团进行的实验中,电子束团的长度决定了该实验的时间分辨率。尤其自由电子激光的高增益辐射过程很大程度上依赖于电子束团的峰值电流强度,因此电子束团长度的测量技术对于一台自由电子激光装置至关重要[1]。
我国在20世纪80年代就开展了自由电子激光的相关研究。1989年,中国科学院高能物理研究所成功研制了振荡器型的北京自由电子激光器(Beijing Free Electron Laser, BFEL)[2],并于1993年实现饱和输出。之后,中国科学院上海应用物理研究所在上海深紫外自由电子激光装置(Shanghai Deep Ultra-Violet Free Electron Laser, SDUV-FEL)[3]上开展高增益型自由电子激光相关的工作,于2010年成功实现了基于高增益谐波(High Gain Harmonic Generation, HGHG)技术的自由电子激光的饱和放大,2011年实现了基于回声效应谐波产生技术(Echo-Enabled Harmonic Generation, EEHG)的自由电子激光的放大实验[4]。2014年,中国科学院上海应用物理研究所承担的X射线自由电子激光试验装置项目正式启动,目前,基建和公用设施已经完成,正在进行设备安装,预计2016年底开始整机调试。SDUV-FEL和X射线自由电子激光试验装置(Shanghai X-ray Free Electron Laser, SXFEL)的电子束主要参数如表 1所示。
| 表 1 SDUV-FEL和SXFEL装置电子束主要参数 Table 1 Main parameters of electron bunches in SDUV-FEL and SXFEL. |
针对自由电子激光装置超短电子束团长度的测量方法主要有:横向偏转腔法(Transverse RF Deflecting Structure, TDS)、电光采样法(Electro-Optical Sampling, EOS)以及自相关法。TDS是直接将电子束团通过一个微波偏转腔进行偏转,下游端束斑垂直尺寸反映束团长度的大小。决定该方法的分辨率因素主要有:偏转腔内的微波功率、电子束流的能量和加速器的束流光学结构。其典型的分辨率为20-50 fs,通过优化电子束流光学,其分辨率可以达到15 fs[5-6]。EOS是利用晶体的Pockels效应,经过晶体的线偏振光在电子束流库伦场的作用下会成为椭圆偏振光,其椭圆度正比于电场强度,对于相对论电子束,可以认为其正比于电子束团的纵向电荷密度。该方法是一种非拦截式的时域测量,主要有4种实现方式:延迟扫描法、光谱解码法、空间解码法、时间解码法,其典型分辨率约为50 fs[7]。自相关法一般测量电子束团产生的相干辐射,当单个电子辐射的波长大于电子束团长度时,束团内的大量电子会产生相干辐射,利用干涉仪测量相干辐射的自相关函数即可反推出电子束团长度。在测量中,最常用的让电子束团产生相干辐射的辐射手段有渡越辐射(Transition Radiation, TR)、衍射辐射(Diffraction Radiation, DR)、同步辐射(Synchrotron Radiation, SR)和Smith-Purcell辐射(Smith-Purcell Radiation, SPR)[8-16]。自相关法作为一种频域测量手段,其时间分辨率可以达到几个飞秒。
与TDS和EOS方法相比,自相关法具有结构简单、造价低廉、时间分辨率高的优势,而相干渡越辐射又是最容易观察的辐射。根据表 1给出的技术指标以及对超短电子束团长度测量方法的研究,我们决定在SDUV-FEL和SXFEL装置上采用相干渡越辐射的研究方法来测量超短电子束团长度。
1 原理与方案设计 1.1 原理当单个相对论性电子穿过铝箔时,由于空间介电常数发生变化,电子会向外辐射电磁波,称为渡越辐射。对于以45°角入射铝箔的单个电子,其反向渡越辐射如图 1所示。
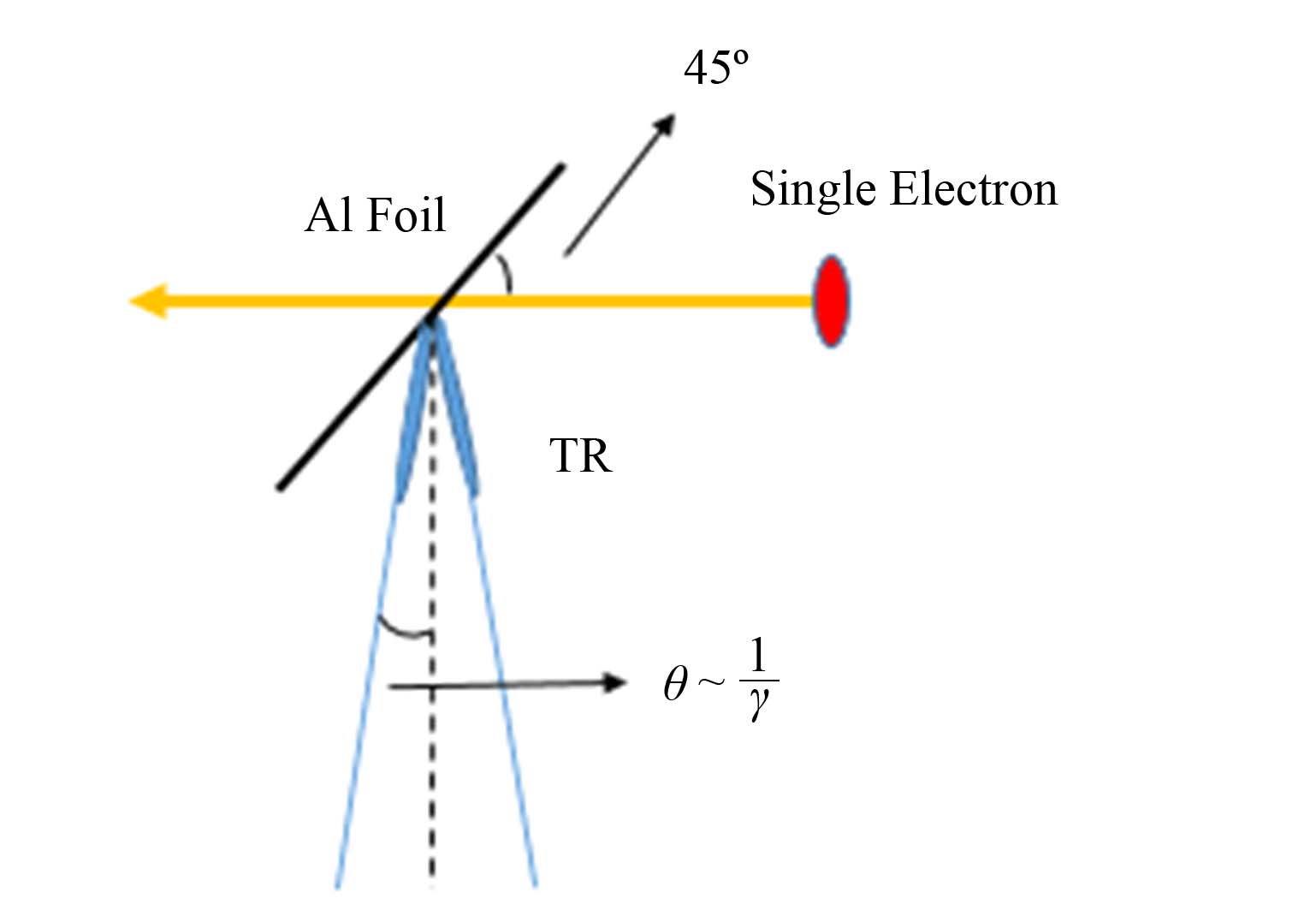
|
图 1 入射角为45°的电子产生的背向渡越辐射示意图 Figure 1 An illustration of backward transition radiation generated by a relativistic electron from 45°-incidence. |
由于铝箔具有良好的导电性,产生的渡越辐射能谱在远红外波段近似为常数,由式(1)给出:
| $\begin{align} & {{I}_{0}}\left( \omega \right)=\frac{{{d}^{2}}E}{d\Omega d\omega }=\frac{{{r}_{e}}mc}{{{\pi }^{2}}} \\ & \frac{{{\beta }^{2}}{{\sin }^{2}}\theta }{{{\left( 1-{{\beta }^{2}}{{\cos }^{2}}\theta \right)}^{2}}} \\ \end{align}$ | (1) |
式中:re为经典电子半径;θ为观测角;m为电子静止质量;β为相对论归一化速度因子;c为光速。以SDUV-FEL装置的电子为例,其能量为150 MeV时,产生的渡越辐射的角分布如图 2所示。由图 2可以看出,单电子渡越辐射主要集中在θ=1/γ附近,γ为洛伦兹因子[9]。
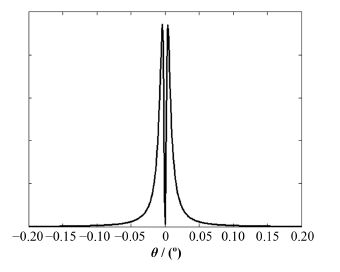
|
图 2 150 MeV单个电子渡越辐射的角分布 Figure 2 Angular distribution of transition radiation spectral energy per solid angle generated by a 150-MeV electron. |
渡越辐射是一种宽谱辐射,当相对论性电子束团穿过铝箔时,就会产生相干渡越辐射,其辐射能谱由式(2)给出:
| ${{I}_{coherent}}\left( \omega ,{{\sigma }_{z}} \right)={{I}_{0}}\left( \omega \right)\left[ N+N\left( N-1 \right) \right]{{F}_{b}}\left( \omega ,{{\sigma }_{z}} \right)$ | (2) |
式中:I0(ω)为单电子的渡越辐射能谱;N为电子束团中电子个数;σz为电子束团纵向长度;Fb(ω, σz)为归一化电子束流纵向分布形状因子,其定义为:
| ${{F}_{b}}\left( \omega ,{{\sigma }_{z}} \right)={{\left| f\left( \omega ,{{\sigma }_{z}} \right) \right|}^{2}}$ | (3) |
| $f\left( \omega ,{{\sigma }_{z}} \right)=\sum\limits_{j=1}^{N}{{{e}^{i\omega {{t}_{j}}}}}\cong N\int_{-\infty }^{\infty }{\rho \left( t,{{\sigma }_{z}} \right){{e}^{i\omega {{t}_{j}}}}}dt$ | (4) |
式中:ρ(t, σz)为电子束团归一化纵向分布。式(4)中tj到t的过渡是因为束团中N个电子同相发射辐射。
对于SDUV-FEL或SXFEL装置上的单个电子束团,N为一个很大的数,为108-109,式(2)可以近似为式(5)[10-11]:
| ${{I}_{coherent}}\left( \omega ,{{\sigma }_{z}} \right)\approx {{N}^{2}}{{I}_{0}}\left( \omega \right){{F}_{b}}\left( \omega ,{{\sigma }_{z}} \right)$ | (5) |
通过迈克尔逊干涉仪可以测得相干渡越辐射的自相关函数:
| $i\left( \tau \right)\propto \int{f\left( t \right)f\left( t+\tau \right)dt}$ | (6) |
对于任何辐射信号,可以证明:
| $\begin{align} & F\left[ \int_{-\infty }^{\infty }{f\left( t \right)\cdot f\left( t+\tau \right)dx} \right]=F\left[ f\left( t \right) \right]\cdot \\ & {{F}^{-1}}\left[ f\left( t \right) \right]={{\left| f\left( \omega \right) \right|}^{2}}={{F}_{b}}\left( \omega \right) \\ \end{align}$ | (7) |
即自相关函数的傅里叶变换为电子束团纵向分布的形状因子,F表示傅里叶变换。由式(5)可知,相干渡越辐射的能谱唯一由电子束团的纵向长度决定。通过测量相干渡越辐射的能谱,并进行曲线拟合,可以反推出电子束团纵向长度。
为得到测量系统对不同辐射频率的响应,标准的红外光源将被用来进行标定。红外光源的辐射遵循黑体辐射的普朗克定律:
| $B\left( \omega \right)=\frac{h{{\omega }^{3}}}{4{{\pi }^{3}}{{c}^{2}}}\frac{1}{{{e}^{h\omega /{{K}_{B}}T}}-1}$ | (8) |
式中:B(ω)为黑体辐射频谱;ħ为约化普朗克常数;c为光速;KB为玻尔兹曼常数。
由于测量系统的物理孔径、分束镜的吸收和反射、以及探测器的特性,实验得到的谱IIRS(ω)与B(ω)必然不一致,测量系统的频谱响应曲线S(ω)由式(9)给出:
| $S\left( \omega \right)=\frac{{{I}_{IRS}}\left( \omega \right)}{B\left( \omega \right)}$ | (9) |
考虑到测量系统的频谱响应,实际测量得到的频谱和自相关曲线分别为式(10)和(11)[12]:
| $K\left( \omega \right)={{F}_{b}}\left( \omega \right)S\left( \omega \right)$ | (10) |
| $k\left( \tau \right)\propto \int{K\left( \omega \right)}{{e}^{i\omega \tau }}d\omega $ | (11) |
为满足SDUV-FEL装置的实验需求和SXFEL装置的工程需求,参考SDUV-FEL和SXFEL装置的技术参数指标,我们自行设计了一套超短电子束团长度测量系统,该系统基于太赫兹(Tera Hertz, THz)迈克尔逊干涉仪,具体的方案设计如图 3所示。该套系统分为三个部分:辐射电磁波发生装置、红外光源标定装置、电子束团长度测量装置。电子束团长度测量装置主要由两个镀金离轴抛物面镜、两个镀金高反射镜以及一个迈克尔逊干涉仪组成。电子束团长度测量装置放置在真空室内部。
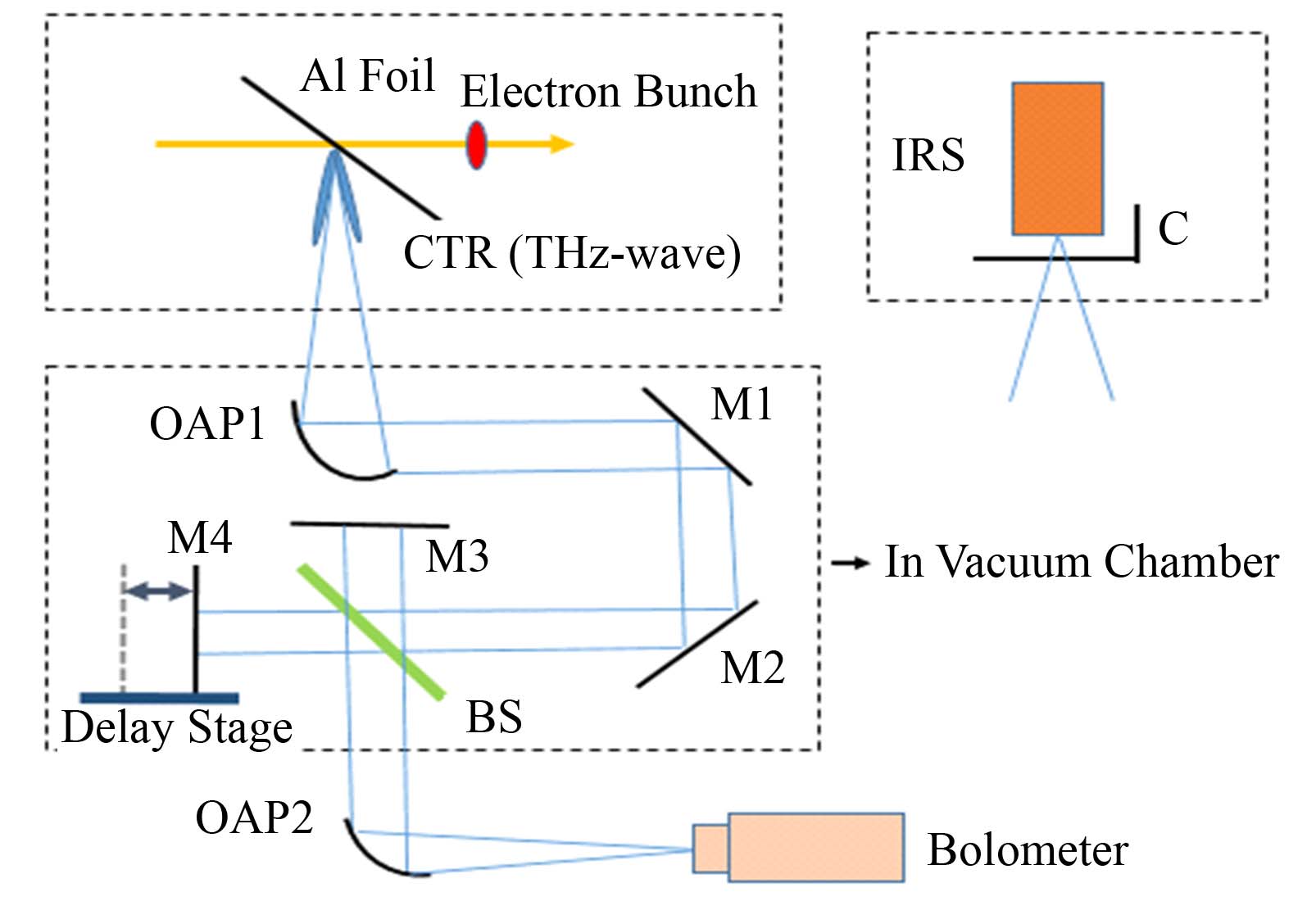
|
图 3 束团长度测量系统原理示意图 IRS:红外光源,OAP:离轴抛物面镜,M:平面镜,BS:分束镜,C:斩波器 Figure 3 A sketch of bunch length measuring system based on CTR. IRS: Infrared light source, OPA: Off-axis parabolic mirror, M: Plain mirror, BS: Beam splitter, C: Optical chopper |
在测量电子束团长度之前,先用红外光源(IRS-001C, IR System)对迈克尔逊干涉仪进行标定和优化。为了使红外光源按照普朗克定律向外辐射THz射波,其灯丝的表面涂有一层黑体涂料(JSC-3, Japan Sensor)。灯丝温度控制在约1173 K。
电子束团以45°入射角穿过25.4 μm厚的铝箔时,由于空间介电常数发生变化,电子会向外辐射电磁波,该电磁波波长位于THz波段范围内。为避免空气对THz波的吸收,电子束团长度测量装置需要处于真空环境中,以利于减小THz传输过程中的造成的能量损耗。同时,辐射电磁波发生装置要离电子束团测量装置尽可能近。此外,由于THz波的发散角较大,需要采用一个镀金离轴抛物面镜来对THz波进行准直。红外光源标定装置向外辐射的THz波被斩波器调制为1 kHz的脉冲信号。THz波经过离轴抛物面镜OAP1变成平行光,再经过平面镜M1、M2的两次反射后,进入厚度为380 µm的50:50的高阻硅分束镜。THz波被分成两束后,一束被固定的平面镜M3反射,另一束被安装在移动平台(MFA-CC, Newport)上的平面镜M4反射。经M3、M4反射回来的两束THz波重叠在一起后发生干涉,产生的干涉光经过离轴抛物面镜OAP2汇聚后,进入探测器进行测量。离轴抛物面镜OAP1、OAP2 (MPD399-M03, Thorlabs)的焦距为228.6mm,直径为76.2 mm。M1-M4反射镜均为镀金高反射率反射镜(PF20-03-M01, Thorlabs),其直径为50.8mm。探测器为液氦冷却的Bolometer (4.2 K system, Infrared Laboratories),其测量波长范围为15-2000μm。通过移动反射镜M4进行测量(步长为1.5 μm),可以得到红外光源THz波的自相关函数。对该自相关函数进行傅里叶变换,可以得到电子束团纵向分布的形状因子。由式(5)可知,相干渡越辐射的能谱唯一由电子束团的纵向长度决定。通过测量相干渡越辐射的自相关函数,并进行曲线拟合,可以反推出电子束团纵向长度[6-11]。
2 参数模拟与讨论在SDUV-FEL和SXFEL装置中,没有经过压缩的电子束团,其纵向分布可以认为是高斯分布:
| $\rho \left( t \right)=\frac{1}{\sqrt{2\pi }{{\sigma }_{z}}}\exp \left( -{{t}^{2}}/2{{\sigma }_{z}}^{2} \right)$ | (12) |
则其形状因子为:
| ${{F}_{b}}\left( \omega \right)=\exp \left( -{{\sigma }_{z}}{{\omega }^{2}} \right)$ | (13) |
由图 4可知,束团长度越短,其束团形状因子覆盖的频谱范围就越宽。在测量中,采用液氦冷却的Bolometer,其频谱覆盖范围为150 GHz-20 THz。如图 4(a)所示,Bolometer的频谱测量范围可以有效覆盖长度为20 fs电子束团的相干渡越辐射频谱。迈克尔逊干涉仪的最短采样步长为1.5 µm,其频谱覆盖范围可以达到100 THz。因此,该装置最短可以测量长度为20 fs的电子束团[16]。对于较长的电子束团,如图 4(b)所示,Bolometer的频谱测量范围可很好覆盖1 ps电子束团的相干渡越辐射频谱,而不能有效覆盖2 ps及更长电子束团的相干渡越辐射频谱。综上所述,该测量系统的有效束团长度测量范围为20 fs-1 ps,时间分辨率可以达到20 fs[13, 17]。
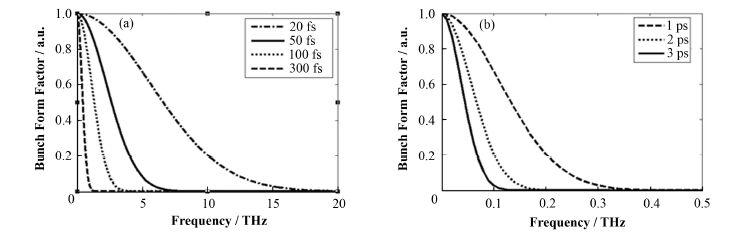
|
图 4 不同束团长度高斯分布的形状因子 (a) 20 fs、50 fs、100 fs、300 fs,(b) 1 ps、2 ps、3 ps Figure 4 Bunch form factor at different electron bunch length with Gaussian shape. (a) 20 fs, 50 fs, 100 fs, 300 fs, (b) 1 ps, 2 ps, 3 ps |
通过系统研究自相关法测量电子束团长度的基本原理,设计了一台基于相干渡越辐射测量电子束团长度的实验系统。设计分析表明,该测量系统的有效束团长度测量范围为20 fs-1 ps,时间分辨率可以达到20 fs。该测量系统结构简单,操作方便,将安装在SXFEL装置上进行实验。现阶段,限制该测量技术的因素主要为Bolometer的频谱响应范围不够宽,如果通过合理布局光路,借助其他类型的探测器拓展频谱范围,时间分辨率有望可以达到几个飞秒。另一方面,自相关法测量电子束团长度基于所有被采样电子束团长度都一样的假设,是一种多次平均的测量,且自相关法作为一种频域测量手段,其解谱过程相对复杂。为了克服自相关法测量的这两个缺陷,今后可以考虑使用光学分光元件和探测器阵列来优化改进基于相干渡越辐射的电子束团长度测量系统[17]。
| [1] | Saldin E L, Schneidmiller E A, Yurkov M V. A simple method for the determination of the structure of ultra-short relativistic electron bunches[J]. Nuclear Instruments and Methods in Physics Research A, 2005, 539: 499–526. DOI: 10.1016/j.nima.2004.11.002 |
| [2] |
谢家麟, 庄杰佳, 钟世才, 等. 北京自由电子激光[J].
强激光和粒子束
, 1989, 1(4): 289–293.
XIE Jialin, ZHUANG Jiejia, ZHONG Shicai, et al. The design and research of Beijing free electron laser facility[J]. High Power Laser and Particle Beams, 1989, 1(4): 289–293. |
| [3] | Zhao Z T, Dai Z M, Zhao X F, et al. The Shanghai high-gain harmonic generation DUV free-electron laser[J]. Nuclear Instruments and Methods in Physics Research A, 2004, 528: 591–594. DOI: 10.1016/j.nima.2004.04.108 |
| [4] | Zhao Z T, Wang D, Chen J H, et al. First lasing of an echo-enabled harmonic generation free-electron laser[J]. Nature Photonics, 2012, 6(6): 360–363. DOI: 10.1038/NPHOTON.2012.105 |
| [5] | Bolzmann A. Investigation of the longitudinal charge distribution of electron bunches at the VUV-FEL using the transverse deflecting cavity LOLA[D]. Hamburg:DESY, 2005. |
| [6] | Hüning M, Bolzmann A, Schlarb H, et al. Observation of femtosecond bunch length using a transverse deflecting structure[C]. Proceedings of the 27th International Free Electron Laser Conference, 2005:538-540. |
| [7] | Steffen B. Electro-optic methods for longitudinal bunch diagnostics at FLASH[D]. Hamburg:DESY, 2007. |
| [8] | Fröhlich L. Bunch length measurements using a Martin-Puplett interferometer at the VUV-FEL[D]. Hamburg:DESY, 2005. |
| [9] | Lihn H, Kung P, Settakorn C, et al. Measurement of subpicosecond electron pulses[J]. Physical Review E, 1996, 53(6): 6413–6418. DOI: 10.1103/PhysRevE.53.6413 |
| [10] |
李智慧, 戴建枰, 杨学平, 等. 利用相干渡越辐射测量电子束团长度的分析与计算[J].
高能物理与核物理
, 2003, 27(9): 831–835.
LI Zhihui, DAI Jianping, YANG Xueping, et al. Analysis and calculation on electron bunch length measurement by using CTR[J]. High Energy Physics and Nuclear Physics, 2003, 27(9): 831–835. |
| [11] |
刘爱琴, 刘征平, 陈永忠, 等. 相干衍射辐射在超短电子束团长度测量中的应用[J].
高能物理与核物理
, 2005, 29(5): 517–523.
LIU Aiqin, LIU Zhengping, CHEN Yongzhong, et al. Analysis and calculation on electron bunch length measurement by using CDR[J]. High Energy Physics and Nuclear Physics, 2005, 29(5): 517–523. |
| [12] | Nozawa I, Kan K, Yang J, et al. Measurement of < 20-fs bunch length using coherent transition radiation[J]. Physical Review Special Topics-Accelerator and Beams, 2014, 17: 072803. DOI: 10.1103/PhysRevSTAB.17.072803 |
| [13] | Murokh A, Rosenzweig J B, Hogan M, et al. Bunch length measurement of picosecond electron beams from a photoinjector using coherent transition radiation[J]. Nuclear Instruments and Methods in Physics Research A, 1998, 410: 452–460. DOI: 10.1016/S0168-9002(98)00177-6 |
| [14] | Thongbai C, Kusoljariyakul K, Rimjaem S, et al. Femtosecond electron bunches, source and characterization[J]. Nuclear Instruments and Methods in Physics Research A, 2008, 587: 130–135. DOI: 10.1016/j.nima.2007.12.023 |
| [15] | Korbly S E, Kesar A S, Temkin R J. Measurement of subpicosecond bunch lengths using coherent Smith-Purcell radiation[J]. Physical Review Special Topics-Accelerator and Beams, 2006, 9: 022802. DOI: 10.1103/PhysRevSTAB.9.022802 |
| [16] | Fröhlich L, Grimm O. Bunch length measurements using a Martin-Puplett interferometer at the VUV-FEL[C]. Proceedings of the 27th International Free Electron Laser Conference, 2005:114-117. |
| [17] | Wesch S, Schmidt B, Behrens C, et al. A multi-channel THz and infrared spectrometer for femtosecond electron bunch diagnostics by single-shot spectroscopy of coherent radiation[J]. Nuclear Instruments and Methods in Physics Research A, 2011, 665: 40–47. DOI: 10.1016/j.nima.2011.11.037 |


