熔化是反应堆严重事故中极为重要和复杂的过程。由于反应堆材料的特殊性和结构的复杂性,很难对反应堆的熔化现象进行准确的研究,所以其详细的物理机制和进程依然很不明确。而现有的研究则多针对于严重事故后熔融物迁移和滞留等行为。普渡大学对堆芯材料熔渣在高压环境下的分布进行了实验模拟,深入探究熔渣的流动分布特点[1]。橡树岭实验室采用真实的反应堆材料,用于测试燃料棒束的严重损伤,探究熔融物的迁移和冷却滞留过程中的行为特征[2]。张小英等[3]以AP600为对象,通过数值模拟研究严重事故下堆芯熔化后熔融物对压力容器壁面的烧蚀过程。此类严重事故的实验研究对于堆芯熔化过程中的细节和瞬态过程相对较少,包括棒内熔化过程中的流动特征、外界条件对熔化过程的影响及熔化过程中形状的具体变化等。
熔化现象在能源领域中的蓄热应用中也得到广泛的研究。Sparrow等[4]通过恒温壁面加热二十烷实验与以纯导热模型为基础的数值计算结果对比,发现实际熔化进程和液相份数的增加超过计算预期结果的50%,说明熔化过程中存在除导热之外的其他传热模式。Chen等[5]通过理论分析得出在圆柱容器内熔化过程中热传导对总体液相份数的作用很小,而且增大斯蒂芬数Ste和高径尺寸比例,有助于熔化进程的加快。Jones等[6]将水浴加热二十烷实验结果与相应的模拟计算结果进行对比,将熔化过程分为4个阶段:纯导热、导热与自然对流、自然对流主导和固相减缩。Shmueli等[7]同样采用焓-多孔介质方法对恒温管壁加热石蜡实验进行计算模拟,提出在熔化初始,热量以热传导方式从管壁至相变材料,此后由自然对流占主要地位,固相呈现圆锥状,并呈现由上至下的逐渐缩减的趋势。天津大学的郭英利[8]对石蜡蓄热材料在圆柱外及球内的蓄热规律进行实验研究,考虑了自然对流以及导热系数对相变的影响。Wang等[9]采用有限体积模型对圆柱容器中相变材料熔化过程进行模拟,计算结果与实验结果吻合较好,且揭示了熔化努塞尔数Nu、熔化所需热量和相变材料的潜热均与斯蒂芬数Ste、傅里叶数Fo和瑞利数Ra相关。然而,目前相关研究多是在圆柱容器外部恒温壁面进行加热,并未关注加热条件和外部边界对熔化进程的影响。
本文采用圆柱容器中心定功率电加热的方式,在恒温水浴、外界自由空气对流以及绝热等外部边界条件下进行熔化实验,研究圆柱容器中熔化的传热机制,并探讨不同参数和边界条件对熔化进程和熔化速率的影响。
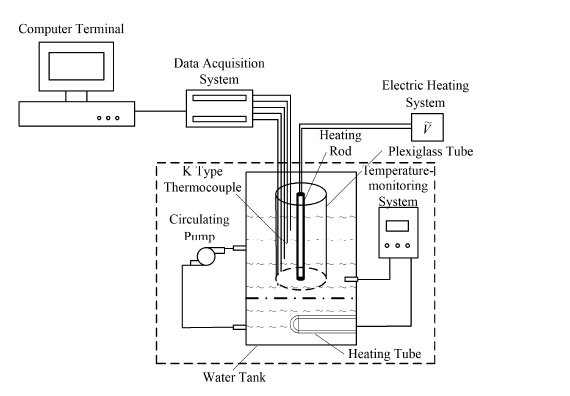
1 实验介绍 1.1 实验装置实验装置示意图见图 1。主要包括不锈钢外壳电加热棒、恒温水浴箱、有机玻璃管、K型铠装热电偶以及电加热系统和数据采集终端。恒温水浴箱能够确保在相变过程中边界温度的恒定。其中循环泵有助于促进水浴温度均匀,温度监测系统对水浴温度进行实时监控,超出阈值则触发加热管的启停。实验初始温度可以在实验前进行设定。数据采集使用吉时利(Keithley)2750系列数据采集系统,实现每3 s进行一次数据采集,同时记录在电脑终端的数据日志中,以便随时保存和查看。
|
图 1 实验装置示意图 Figure 1 Schematic of the experimental apparatus. |
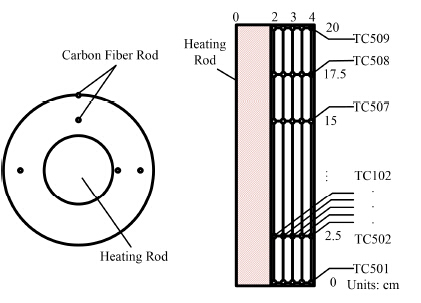
实验过程中的石蜡温度由45个K型热电偶所测。其布置位置如图 2所示,分为5列,每列各为9个,并间隔25 mm布置在不同的高度。为尽量减少因热电偶位置所带来的影响,将每列布置在不同的方位,但是每列径向位置间隔5 mm。
|
图 2 热电偶位置示意图 Figure 2 The position of thermocouples. |
实验采用的相变材料是商用石蜡。石蜡具有低熔点和相变过程中无过冷现象的特性,经常被用于相变实验。根据差示扫描量热法所测结果,本实验采用的石蜡熔点为56.0-58.1 ºC,固液相变潜热为210.0 J∙g-1,固态比热容为6.6 J∙g-1∙k-1,液态为2.6J∙g-1∙k-1。除此之外,液体石蜡的密度随着温度升高而减小,例如60 ºC时约为800 kg∙m-3,在90 ºC时约为770 kg∙m-3。
1.3 实验方法如图 1所示,有机玻璃圆柱空腔高250 mm,壁厚5 mm,内径为80 mm,盛装有高度为200 mm的固体石蜡。固体石蜡体积为0.00084 m3,上部与空气接触。实验开始前,将整个容器放置于水浴槽内,直到整个区域温度达到初始设定值,实现腔壁恒温条件。此外,将装置静置于室内得到自由空气对流边界换热条件,采用石棉绝热材料包裹圆柱空腔方式,以近似得到绝热边界条件。
1.4 实验内容已进行的实验内容见表 1。在水浴温度为50 ºC的恒温边界条件下,进行了加热功率分别为50 W、100 W、150 W、200 W的4组熔化实验,以及在空气对流换热边界和绝热边界条件下,进行了加热功率为100 W的两组实验。为对比水浴温度对熔化的影响,还进行了水浴温度为20 ºC、功率为100 W的实验。
| 表 1 实验内容 Table 1 Content of experiments. |
考虑到熔化过程中液体区域存在的流动,流函数应该是光滑且具有空间二阶可微的特性。所以在重建温度场以及相变界面时,采用二维三次插值或者三次样条插值方法。该插值方法设定温度插值函数为在插值平面区域内二阶可微的三次多项式,在满足给定节点的温度值的同时考虑边界条件,保证温度场的光滑可微特征。在温度高于58.1 ºC的区域视为液体区域,并根据径向位置进行加权处理,由此可得不同时刻的相变界面以及液相份数(熔化体积与初始体积之比)。
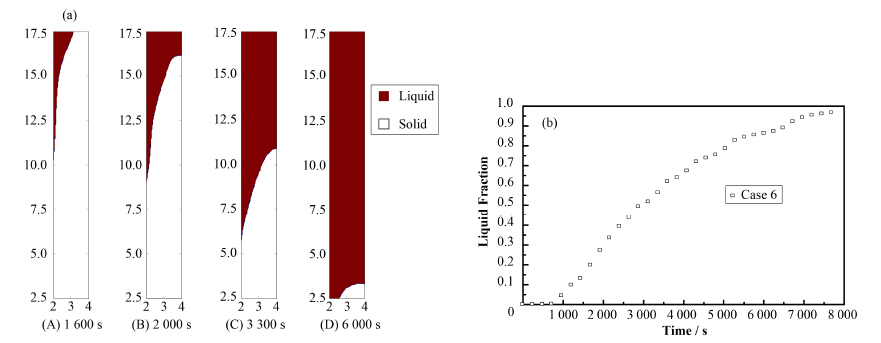
图 3(a)为在自由空气对流边界下加热功率为100 W不同时刻的相变界面。整体熔化呈现从上至下,从内到外的趋势,将其分为4个阶段:1) 在初始阶段,近棒区域的固体石蜡通过纯导热的方式被加热,然后开始熔化;2) 随着熔化的进行,液相部分逐渐增加,靠近加热棒的液体石蜡温度升高,密度减小,开始上升形成自然对流。自然对流的加剧形成如图 3(A)所示,在靠近加热棒上部区域呈现加快熔化的现象;3) 自然对流的进一步加剧,造成圆柱空腔内上部区域全部熔化,形成液相区域,开始明显的由上至下的熔化趋势(图 3(B)和(C)),自然对流换热在石蜡熔化过程中占主导地位;4) 直至熔化进程后期,液相石蜡占大部分区域(图 3(D))。该趋势与Jones等[6]研究结果类似。 相应地,在不同的熔化阶段,液相份数的变化情况不同。图 3(b)中以纯导热为传热机制的起始阶段,液相份数由零开始缓慢增加。产生自然对流之后,随着对流换热加剧且逐渐占主导地位,熔化份额也快速增加。熔化后期阶段,随着边界热量的损失以及相变界面的减小,液相体积增加缓慢,直至完全熔化。
|
图 3 熔化不同时刻的相变界面(a)和液相份数(b) Figure 3 Solid-liquid interface (a) and liquid fraction (b) at different moments. |
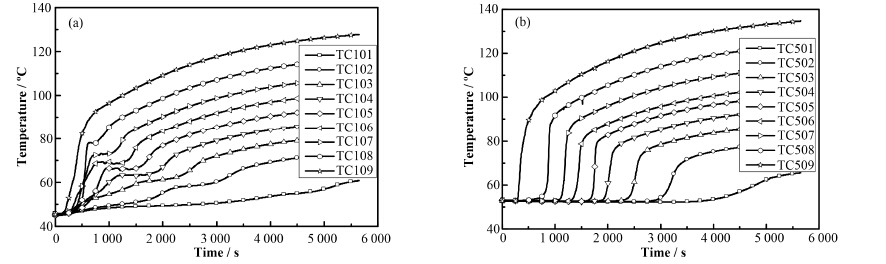
在功率为100 W、实验过程中恒温水浴保持在50 ºC的实验条件下,获得了热电偶测点的温度随时间变化的数据。如图 4(a)和(b)分别为径向距离2 cm (TC101-109)和4 cm (TC501-509)处不同高度的热电偶温度数据。
|
图 4 径向2 cm (a)和4 cm (b)处不同高度的温度变化 Figure 4 emperature change at different height for radial location of 2 cm (a) and 4 cm (b). |
实验初期,径向热传导致使靠近加热棒的不同高度的石蜡温度急速地升高,如图 4(a)所示。且在1000 s时,径向2 cm处高度大于5 cm的固体石蜡已经熔化。此阶段呈现由内向外的熔化趋势,随之导致在高处区域熔化加快,见图 3(A)。不同于图 4(a),距离加热棒较远的径向4 cm处,图 4(b)中的温度曲线具有较明显的依次上升的特点,说明在该处的熔化过程中受到对流传热的影响加大。随着径向距离的增加,外层区域受到的流动影响更为明显。
当两相交界面移动某处测温点时,通过交界面向固体区域的热传导的加强导致该处石蜡温度上升至熔化,熔化后的液体参与交界面的临近流动中,流动上游的高温液体流经此处致使该处温度骤然上升,直至该处流动达到相对稳定。之后受到加热棒的持续加热,该处温度开始缓慢上升。
熔化过程中后期,在液体区域形成明显的温度分层现象,因此该区域主要通过热传导从上部向下部导热,而受浮力驱动形成的自然对流在该区域并不明显。存在近棒处的上升流动和沿两相界面处向下的流动,形成涵盖液体区域的对流循环。
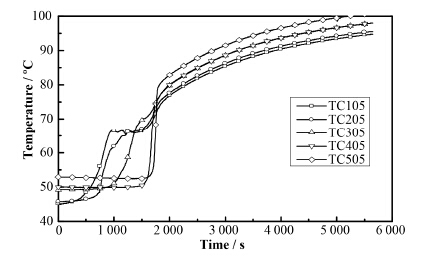
值得注意的是,图 4(a)中存在温度平稳现象。该现象温度高于石蜡熔点,具有位置越低,温度越低,平稳现象出现越晚,持续时间也越久的特点。考虑到近棒处剧烈的自然对流,来自加热棒的绝大部分热量被当地的上升的自然对流带走,上升至高处液体区域。受到石蜡本身较低的热导率和绝大部分液体区域中微弱的对流流动造成的传热限制,热量很难从上部传递到下部区域,这导致在较低液体区域不存在明显的热量输入和输出差异,从而温度平稳现象出现。图 5为同一水平高度的温度变化情况。在1500 s前,尽管在不同径向位置存在初始温度少许差异,但是温度上升次序依然为由内到外,并且在径向2 cm和2.5 cm处形成明显的温度平稳现象。约1500 s时,最外层4 cm石蜡开始熔化,该水平位置处温度分层形成,此后温度平稳现象结束,温度开始再次升高。
|
图 5 高度为10 cm不同径向位置处的温度变化 Figure 5 Temperature change at height of 10 cm for different radial location. |
实验1-4为不同加热功率在相同边界水浴恒温边界下的熔化过程。斯蒂芬数Ste是表征热源条件对熔化过程影响的重要无量纲常数[10]。定义本实验条件下修正Ste为:
| $Ste={{c}_{pl}}\left( q''h/k \right)/L$ | (1) |
式中:cpl为液相的热容;q"为不考虑加热棒升温所需热量情况下加热壁面的面热流密度;h为熔化对象高度;k为液相的导热系数;L是熔化材料的潜热。
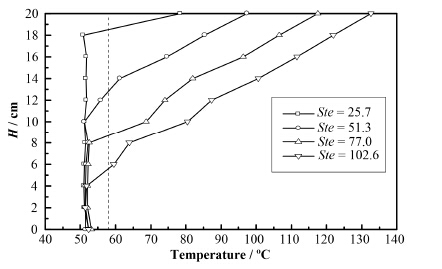
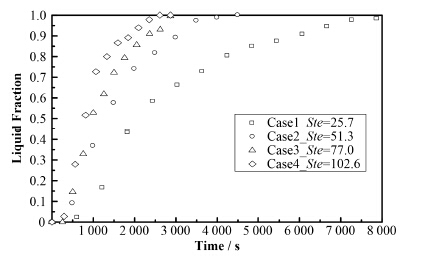
图 6是1000 s时不同实验中径向位置为3 cm处的温度。此时较低Ste数(功率分别为50 W和100 W)下,12 cm高度以下的石蜡仍为固态。而高Ste数时分别仅剩余10 cm和6 cm高度的固相石蜡。因此提高Ste数,能够明显加快熔化过程。图 7是不同Ste数对熔化份额的影响。相对于较低的Ste=25.7、Ste=51.3的情况下液相份数增加明显加快,全部熔化所需时间更短。而对于更高的Ste情况下,熔化进程也具有同样的加快趋势,但促进程度则相对较弱,即在高Ste数情况下进一步提高加热功率或者提高Ste数对熔化进程的促进效果减弱。
|
图 6 1000 s时高度为10 cm、径向3 cm处温度 Figure 6 Temperature at height of 10 cm for radial location of 3 cm at 1000 s. |
|
图 7 不同Ste数下液相份数的变化 Figure 7 Liquid fraction to different Stefan numbers. |
初始条件对熔化进程具有不可忽视的影响,定义过冷度公式如下[11]:
| ${{S}_{c}}={{c}_{pl}}\left( {{T}_{m}}-{{T}_{i}} \right)/L$ | (2) |
式中:Tm是熔化材料熔点;Ti是初始温度。
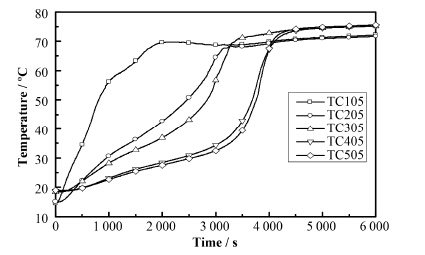
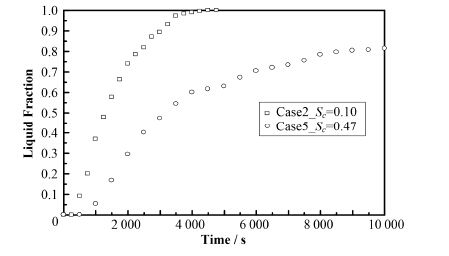
图 8是实验5 (Sc=0.47)中高度为10 cm处,不同径向位置的温度变化情况。该条件下,由于较低的边界温度,平稳现象并不明显。图 9是两种条件下的液相份数的变化情况。较低的边界温度导致较大的热损失,温度达到稳定时的温度值较低,并且较大的过冷度,致使熔化份额的增加变缓,并且趋于水平,即熔化最终将达到稳定的热平衡,出现稳定的固液交界面形状。减小过冷度或提高边界温度对于加快熔化进程具有明显的促进作用。
|
图 8 实验5中高度为10 cm处不同径向位置的温度变化 Figure 8 Temperature change at height of 10 cm for different radial locations in Case 5. |
|
图 9 不同Sc数下液相份数的变化 Figure 9 Liquid fraction to different sub-cooling parameters. |
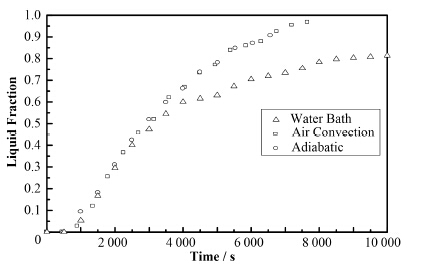
不同边界条件下的熔化速率见图 10。在初始的阶段,边界条件对熔化速率的影响并不明显,三种边界下液相份数变化相同。在3000 s后,恒温边界的液相份数显著低于其他两种边界情况,因此恒温边界更有利于热量的散出。而空气对流和绝热两种边界条件对整个熔化份额变化的影响差异不大。
|
图 10 不同边界条件下液相份数的变化 Figure 10 Liquid fraction under different boundary conditions. |
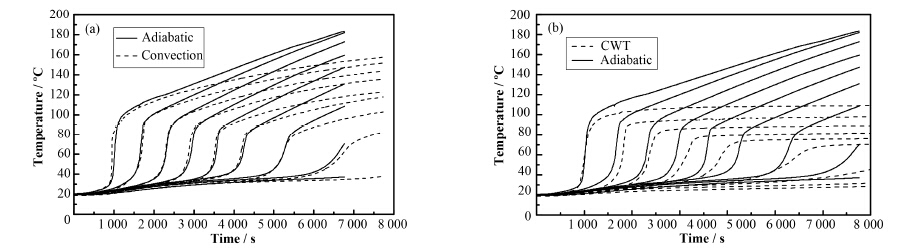
空气对流和绝热两种边界下石蜡温度变化情况对比见图 11(a)。较高位置温度上升最快。空气对流和绝热两种边界条件对熔化进程的影响仅在于熔化后液体温度的差异。而受到石蜡本身导热限制,这种液体温度的差异对固体熔化速率影响较小。绝热边界和恒温边界条件下的熔化温度变化差异见图 11(b)。在开始阶段,边界温度对熔化过程影响较小。随着熔化时间的进行,固体石蜡熔化过程中受到较低边界温度的影响越来越大,热量损失过大,使得熔化进程减慢。
|
图 11 绝热和空气对流(a)、恒温(b)边界条件下径向4 cm处的温度变化 Figure 11 Temperature change under conditions of air convection (a),water bath (b) and adiabatic boundary for radial location of 4 cm. |
旨在对反应堆堆芯熔化这一复杂现象进行预研,本文对中心圆柱空腔中石蜡进行熔化实验。在实验中认识到熔化过程中存在的自然对流、熔化材料的热导率、边界条件以及初始条件对熔化进程有很大的影响。通过改变加热功率、边界条件等,对比不同条件下熔化过程中温度变化情况和特点,以及不同条件对熔化份额的影响,得出以下结论:
1) 熔化开始阶段,自然对流产生后,加快上部区域的熔化,开始形成整体从上到下的熔化趋势。随着自然对流的加剧,并逐渐在熔化进程中占据主要地位,加快熔化进程。在熔化后期,液体区域呈现明显的温度分层现象。
2) 初始温度接近熔点的熔化实验中,近棒区域的较低位置出现温度平稳现象,并且水平位置越低,出现时间越晚,持续时间越长。在某一水平处固体石蜡熔化后,温度平稳现象结束,温度继续上升。
3) 增加Ste数和降低过冷度Sc对提高熔化速率具有显著的作用。然而受到石蜡本身低热导率的限制,在相同功率和初始温度条件下,不同边界对熔化前期进程的影响不大,只在中后期出现液相温度上较大的差别。空气对流边界和绝热边界对熔化速率的影响无明显的差异。
| [1] |
Wu Q, Kim S, Ishii M, et al. High pressure simulation experiment on corium dispersion in direct containment heating[J].
Nuclear Engineering and Design, 1996, 164 (1-3) : 257 –269.
DOI: 10.1016/0029-5493(96)01222-8 ( 0) 0)
|
| [2] |
Ott L J, Hagen S. Interpretation of the results of the CORA-33 dry core boiling water reactor test[J].
Nuclear Engineering and Design, 1997, 167 (3) : 287 –306.
DOI: 10.1016/S0029-5493(96)01305-2 ( 0) 0)
|
| [3] |
张小英, 姚婷婷, 李志威, 等. 堆芯熔融物对压力容器壁面烧蚀过程的数值模拟[J].
核技术, 2015, 38 (2) : 020606 .
DOI: 10.11889/j.0253-3219.2015.hjs.38.020606 ZHANG Xiaoying, YAO Tingting, LI Zhiwei, et al. Numerical simulation of the ablation process of the nuclear pressure vessel heated by core melt[J]. Nuclear Techniques, 2015, 38 (2) : 020606 . DOI: 10.11889/j.0253-3219.2015.hjs.38.020606 (  0) 0)
|
| [4] |
Sparrow E M, Broadbent J A. Inward melting in a vertical tube which allows free expansion of the phase-change medium[J].
Journal of Heat Transfer, 1982, 104 (2) : 309 –315.
DOI: 10.1115/1.3245089 ( 0) 0)
|
| [5] |
Chen W Z, Chen S M, Liu Z, et al. Study of contact melting inside isothermally heated vertical cylindrical capsules[J].
Journal of Thermal Science, 1993, 2 (3) : 190 –195.
DOI: 10.1007/BF02650856 ( 0) 0)
|
| [6] |
Jones B J, Sun D, Krishnan S, et al. Experimental and numerical study of melting in a cylinder[J].
International Journal of Heat and Mass Transfer, 2006, 49 (15-16) : 2724 –2738.
DOI: 10.1016/j.ijheatmasstransfer.2006.01.006 ( 0) 0)
|
| [7] |
Shmueli H, Ziskind G, Letan R, et al. Melting in a vertical cylindrical tube:numerical investigation and comparison with experiments[J].
International Journal of Heat and Mass Transfer, 2010, 53 (19) : 4082 –4091.
DOI: 10.1016/j.ijheatmasstransfer.2010.05.028 ( 0) 0)
|
| [8] |
郭英利.石蜡圆管外相变蓄热与释热规律的研究[D].天津:天津大学, 2008
GUO Yingli.Study on the heat storage and heat release by paraffin phase change outside the pipe[D].Tianjin:University of Tianjin, 2008 http://cdmd.cnki.com.cn/article/cdmd-10056-2009071544.htm (  0) 0)
|
| [9] |
Wang S M, Faghri A, Bergman T L. Melting in cylindrical enclosures:numerical modeling and heat transfer correlations[J].
Numerical Heat Transfer Part A:Applications An International Journal of Computation & Methodology, 2012, 61 (11) : 837 –859.
DOI: 10.1080/10407782.2012.672895 ( 0) 0)
|
| [10] |
Kumar L, Manjunath B S, Patel R J, et al. Experimental investigations on melting of lead in a cuboid with constant heat flux boundary condition using thermal neutron radiography[J].
International Journal of Thermal Sciences, 2012, 61 : 15 –27.
DOI: 10.1016/j.ijthermalsci.2012.06.014 ( 0) 0)
|
| [11] |
Zhang Y, Chen Z, Wang Q, et al. Melting in an enclosure with discrete heating at a constant rate[J].
Experimental Thermal and Fluid Science, 1993, 6 (2) : 196 –201.
DOI: 10.1016/0894-1777(93)90029-I ( 0) 0)
|


