镎是后处理中仅次于铀和钚的重要核材料[1]。从环境、安全和资源利用等方面考虑,后处理中实现对镎的分离和回收具有重要意义。目前,商业后处理厂均采用水法Purex流程进行乏燃料后处理。由于镎的化学性质复杂,其在Purex流程中的走向分散,这给镎的分离和回收带来许多困难。近年来,随着动力堆燃耗的不断提高,美国、法国、日本、印度等许多国家针对高燃耗乏燃料开展了先进Purex流程的研究[2]。先进Purex流程中的一个重要特点是将镎与铀钚共同萃取,避免镎进入高放废液,并实现镎的全分离和回收。在先进Purex流程中,镎与铀钚共萃取后的走向有多种选择,例如将镎与铀钚共反萃,所得产品可用于快堆燃料,如果将镎与铀钚分离则可以简化流程,降低后续纯化铀和钚的难度。针对镎与铀钚的分离,近年来的研究发现肼类衍生物对Np(VI)和Pu(IV)的氧化还原反应具有明显的选择性,它们还原Np(VI)的反应速度明显快于与Pu(IV)的反应,利用这一特性,有望达到镎与铀钚分离的目的[3-4]。Yasutoshi等[5-6]以烯丙基肼为还原剂进行了镎与铀钚的分离实验,水相产品中含有91%的Np、1%的Pu和0.004%的U。张先业等[7-8]研究了甲基肼还原Np(VI)的动力学研究,并开展了U-Np分离工艺的相关研究。
目前,关于水相中肼类衍生物还原Np(VI)和Pu(IV)反应机理、动力学等方面的研究已经有大量文献报道[9-10]。与水相还原过程相比,两相还原反萃过程除了镎钚还原过程外,还包含了镎钚在两相间分配过程,更贴近实际工艺过程。因此,研究Np(VI)和Pu(IV)的还原反萃过程对实际工艺具有重要的指导作用。基于以上想法,本工作选取硝酸肼、甲基肼和偏二甲基肼作为还原剂,系统考察还原剂浓度、硝酸浓度、温度等因素对还原反萃Np(VI)和Pu(IV)的影响,本文为硝酸肼还原反萃取Np(VI)和Pu(IV)的动力学系列研究之一。
1 实验部分 1.1 仪器与装置FJ414型低本底α闪烁探头、α能谱仪(北京核仪器厂);UV-1000紫外可见分光光度计(中国Lab-Tech公司);自制单级实验装置。
1.2 试剂及配置方法Np(VI)溶液:采用H型带隔膜的玻璃电解池,铂网作为阳极,钛片作为阴极,控制电流密度为30mA∙cm-2进行电解氧化。镎浓度分析采用烤盘测α计数法。
Pu(IV)溶液:对含钚料液进行调酸,调价,再采用2606阴离子交换树脂进行离子交换制备Pu(IV)溶液。钚浓度分析采用烤盘测α计数法。
Np(VI)和Pu(IV)有机相料液:调节Np(VI)或Pu(IV)溶液的硝酸浓度至指定值,采用硝酸预平衡的30% TBP/煤油对含Np(VI)或Pu(IV)的溶液进行萃取,分析Np(VI)或Pu(IV)浓度。
1.3 实验方法和数据处理将确定组成的水相和有机相按体积加入单级实验设备中,按预定时间点取样,离心分相后分析水相和有机相中镎或钚的浓度。
1.3.1 Np(VI)还原反萃动力学方程参考相关反应动力学文献[11-12],假设反应对[Np(VI)]o和[Np(V)]a为一级反应。Np(VI)还原反萃速率表达式为式(1) :
| $\begin{array}{*{20}{l}} {r = {k_f}{{\left[ {Np\left( {VI} \right)} \right]}_o}{{\left[ {HN{O_3}} \right]}_a}^n{{\left[ {{N_2}{H_4}} \right]}_a}^m - }\\ {{k_r}{{\left[ {Np\left( V \right)} \right]}_a}{{\left[ {HN{O_3}} \right]}_a}{{^n}^\prime }{{\left[ {{N_2}{H_4}} \right]}_a}^m} \end{array}$ | (1) |
式中:[Np(VI)]o和[Np(V)]a分别为有机相Np(VI)浓度和水相Np(V)浓度。依据物料衡算得出式(2) :
| $\begin{array}{l} N{p_{total}} = V \times {\left[ {Np\left( V \right)} \right]_a} + V \times {\left[ {Np\left( {VI} \right)} \right]_a} + \\ L \times {\left[ {Np\left( V \right)} \right]_o} + L \times {\left[ {Np\left( {VI} \right)} \right]_o} \end{array}$ | (2) |
式中:V为水相体积;L为有机相体积。
假设Np(V)不被萃取,相比1:1条件下由式(2) 简化得到式(3) :
| $x + \frac{{1 + D}}{D}y = 1$ | (3) |
式中:D为Np(VI)分配比;x=[Np(V)]a/[Np(V)]o0;y=[Np(VI)]o/[Np(V)]o0。其中:[Np(V)]o0为初始有机相Np(VI)浓度。在保持硝酸浓度和硝酸肼浓度恒定的条件下,结合式(1) 和式(3) ,得到式(4) :
| $\begin{array}{l} \frac{{d{{[Np(V)]}_a}}}{{dt}} = ( - \frac{{1 + D}}{D}) \times (\frac{{d{{[Np(VI)]}_o}}}{{dt}})\\ = {k_f}^\prime {[Np(VI)]_o} - {k_r}^\prime {[Np(V)]_a} \end{array}$ | (4) |
式中:kf'=kf[HNO3]n[N2H4]m;kr'=kr[HNO3]an' [N2H4]am'。将式(3) 代入式(4) 中最终化简得:
| $\frac{{dx}}{{dt}} = {k_f}^\prime \times \frac{D}{{1 + D}}(1 - x) - {k_r}^\prime x = A - Bx$ | (5) |
式中:
在[0, t]区间对式(5) 进行积分,则得式(6) :
| $x = \frac{A}{B}(1 - {e^{ - Bt}})$ | (6) |
以上推导表明:如果假设正确,以[Np(V)]a/[Np(V)]o0对时间t作图,所得曲线应符合e指数函数y=a(1-e-bt)。拟合曲线得到相关参数 A、B。再计算可以得出kf'、kr',再分别以ln(kf')和ln(kr')对相应的ln[HNO3]和ln[N2H4]作图,可确定硝酸浓度和硝酸肼浓度的反应级数,最终确定动力学方程。
1.3.2 Pu(IV)还原反萃动力学方程假设反应对[Pu(IV)]o为一级反应,速率表达式为式(7) :
| $ - d{[Pu(IV)\left] {_o/dt = k} \right[Pu\left( {IV} \right)\left] {_o} \right[HN{O_3}\left] {^n} \right[{N_2}{H_4}]^m}^{}$ | (7) |
式中:[Pu(IV)]o为有机相Pu(IV)浓度。
在保持硝酸浓度和硝酸肼浓度不改变的条件下,得式(8):
| $ - d{\left[ {Pu\left( {IV} \right)} \right]_o}/dt = k'{\left[ {Pu\left( {IV} \right)} \right]_o}$ | (8) |
式中:k'= k[HNO3]n[N2H4]m。
对式(8) 积分,并整理得式(9) :
| $ln({[Pu(IV)\left] {{{_o}^t}/} \right[Pu(IV)]_o}^0) = - k't$ | (9) |
式中:[Pu(IV)]ot/[Pu(IV)]o0为t时刻有机相Pu(IV)浓度与初始有机相Pu(IV)浓度的比值。以上推导表明:以ln([Pu(IV)]ot/[Pu(IV)]o0)对t作图,所得图形应为直线。该直线的斜率即为相应条件的k'。再以ln(k')分别对相应的ln[HNO3]和ln[N2H4]作图,其直线斜率为硝酸浓度和硝酸肼浓度的反应级数。进一步计算k值,得出硝酸肼还原反萃钚的动力学方程。
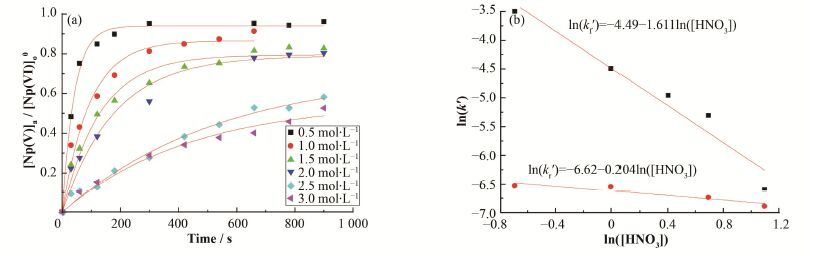
2 结果与讨论 2.1 硝酸肼还原反萃Np(VI) 2.1.1 反应对硝酸浓度级数的确定在T=20 C、[Np(VI)]o0=40 mg∙L-1、[N2H4]= 0.25mol∙L-1条件下,考察[HNO3]=0.5-3.0 mol∙L-1时,有机相Np浓度随时间的变化。由Np(VI)分配比计算得到[Np(V)]a/[Np(VI)]o0随时间t的曲线,如图 1(a)所示。对图 1(a)中曲线进行非线性拟合,曲线符合方程y=a(1-e-bt),由此表明反应对[Np(VI)]o和[Np(V)]a为一级反应,所设式(1) 正确。
|
图 1 硝酸浓度反应级数的确定 (a) [Np(V)]a/[Np(VI)]o0与时间的关系,(b) ln(k')与ln([HNO3])的关系 Figure 1 Determination of reaction orders with respect to concentration of HNO3. (a) Relationship between [Np(V)]a/[Np(VI)]o0 and time, (b) Relationship between ln(k') and ln([HNO3]) |
采用曲线拟合得出kf'和kr',并以ln(k')对ln([HNO3])做图,如图 1(b)所示,所得直线斜率为水相硝酸浓度的反应级数,即水相硝酸浓度反应级数分别为n=-1.6和n'=-0.2。此结果表明,降低硝酸浓度可以同时加快正反应速度和逆反应速度,并且硝酸浓度对正反应的影响更大。
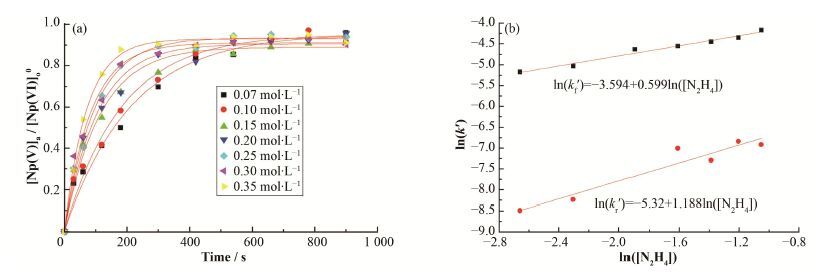
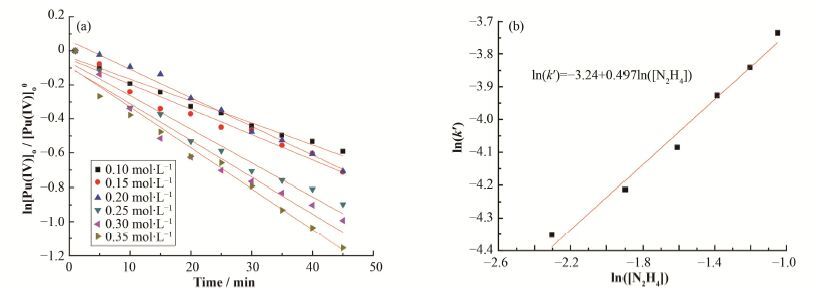
2.1.2 反应对硝酸肼浓度级数的确定在T=20 C、[Np(VI)]o0=40 mg∙L-1、[HNO3]= 1mol∙L-1、硝酸肼浓度为0.07-0.35 mol∙L-1条件下,得到[Np(V)]a/[Np(VI)]o0随时间t的变化曲线,如图 2(a)所示,通过曲线拟合确定k'。再作ln(k')对ln([N2H4])的关系曲线如图 2(b)所示,所得斜率即为水相硝酸肼浓度的反应级数,即m=0.6和m'=1.2(图 2)。因此,提高硝酸肼浓度可以同时加快正反应速度和逆反应速度,并且硝酸肼浓度对逆反应的影响更大。
|
图 2 硝酸肼浓度反应级数的确定 (a) [Np(V)]a/[Np(VI)]o0与时间的关系,(b) ln(k')与ln([N2H4])关系 Figure 2 Determination of reaction orders with respect to concentration of hydrazine. (a) Relationship between [Np(V)]a/[Np(VI)]o0 and time, (b) Relationship between ln(k') and ln([N2H4]) |
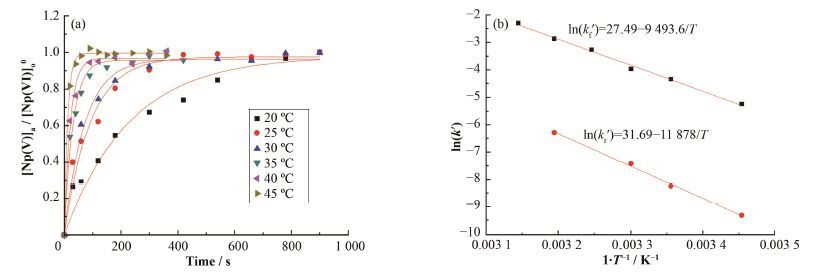
在[Np(VI)]o0=40 mg∙L-1、[HNO3]=1 mol∙L-1、[N2H4]=0.25 mol∙L-1和温度范围为20-45 C条件下,对[Np(V)]a/[Np(VI)]o0随时间t的变化曲线进行非线性拟合,得出k值,如图 3(a)所示。根据阿伦尼乌斯公式lnk=lnA-Ea/(RT),以ln(k')对1/T做图,如图 3(b)所示。图 3(b)中直线的斜率代表反应的表观活化能,即肼还原反萃Np(VI)的表观活化能分别为Ea(f)=(78.9±0.3) kJ∙mol-1和Ea(r)= (98.8±0.5) kJ∙mol-1。
|
图 3 反应活化能的确定 (a) [Np(V)]a/[Np(VI)]o0与时间的关系,(b) ln(k')与1/T关系 Figure 3 Determination of activation energy. (a) Relationship between [Np(V)]a/[Np(VI)]o0 and time, (b) Relationship between ln(k') and 1/T |
根据式(1) 计算得出温度20 C相对应的kf和kr值,结果列于表 1。由一系列的kf和kr取平均值,分别得出kf=(2.78±0.32) ×10-2mol∙L-1∙s-1和kr= (6.08±1.3 )×10-3mol∙L-1∙s-1。
| 表 1 kf和kr值的确定 Table 1 Determination of kf and kr. |
通过以上实验,最终确定了有机相Np(VI)还原反萃动力学方程如下所示:
| $\begin{array}{l} d\left[ {Np\left( V \right)} \right]/dt = {k_f}{\left[ {Np\left( {VI} \right)} \right]_o}{\left[ {HN{O_3}} \right]_a}^{ - 1.6}{\left[ {{N_2}{H_4}} \right]_a}^{0.6} - \\ {k_r}{[Np(V)]_a}{[HN{O_3}]_a}^{ - 0.2}{[{N_2}{H_4}]_a}^{1.2} \end{array}$ | (10) |
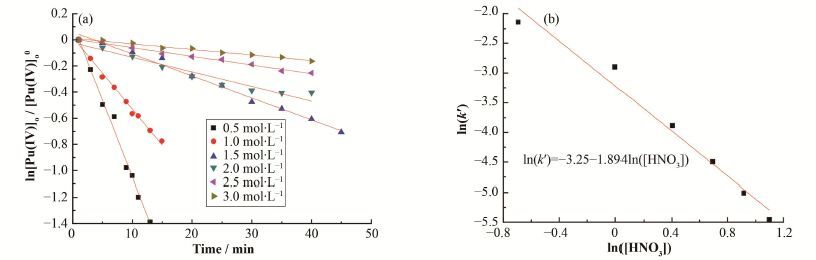
在T=18 C、[Pu(IV)]o0=14 mg∙L-1、[N2H4]= 0.2mol∙L-1和[HNO3]=0.5-3.0 mol∙L-1条件下,考察[HNO3]=0.5-3.0 mol∙L-1时,有机相Pu浓度随时间的变化,以ln[Pu(IV)]o/[Pu(IV)]o0对t作图,如图 4(a)所示。图 4(a)中图形均符合线性关系,这表明反应对[Pu(IV)]o为一级反应,所设的硝酸肼还原反萃Pu(IV)动力学方程正确。对图 4(a)中直线进行拟合,得到不同硝酸浓度对应的k'值。再以ln(k')对ln(HNO3)作图,如图 4(b)所示,图 4(b)中直线斜率代表硝酸浓度反应级数,即水相硝酸浓度的反应级数为n=-1.9。由此可知,提高硝酸浓度可以减慢反应速度。
|
图 4 硝酸浓度反应级数的确定 (a) ln[Pu(IV)]o/ [Pu(IV)]o0与时间的关系,(b) ln(k')与ln([HNO3])关系 Figure 4 Determination of reaction orders with respect to concentration of HNO3. (a) Relationship between ln[Pu(IV)]o/ [Pu(IV)]o0 and time, (b) Relationship between ln(k') and ln([HNO3]) |
在T=18 C、[Pu(IV)]o0=14 mg∙L-1、[HNO3]= 1.5mol∙L-1和水相[N2H4]=0.1-0.35 mol∙L-1条件下,得出ln[Pu(IV)]o/[Pu(IV)]o0与t关系曲线(如图 5(a)所示),对曲线进行拟合,得出k'值。再以ln(k)对ln([N2H4])曲线,如图 5(b)所示,确定水相硝酸肼反应级数为m=0.5。由此得出降低硝酸肼浓度可以减慢反应速度。
|
图 5 硝酸肼浓度反应级数的确定 (a) ln[Pu(IV)]o/ [Pu(IV)]o0与时间的关系,(b) ln(k')与ln(N2H4])关系 Figure 5 Determination of reaction orders with respect to concentration of hydrazine. (a) Relationship between ln[Pu(IV)]o/ [Pu(IV)]o0 and time, (b) Relationship between ln(k') and ln([N2H4]) |
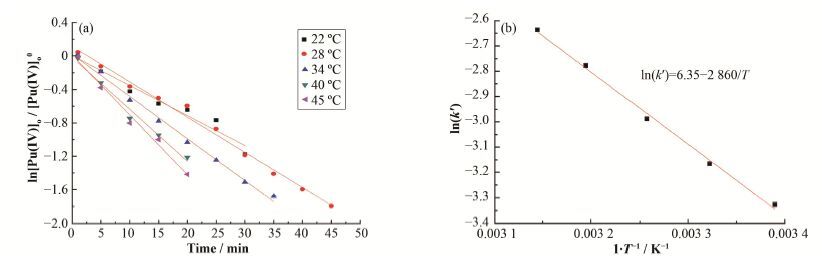
在反应温度范围为22-45 C,将ln[Pu(IV)]o/[Pu(IV)]o0对t作图,如图 6(a)所示,得到不同反应温度下k'值。根据阿伦尼乌斯公式lnk=lnA-Ea/(RT),以ln(k')对1/T做图,如图 6(b)所示。图 6(b)中直线的斜率代表还原反萃过程的表观活化能,即反应的表观活化能为:Ea=(23.8±0.1) kJ∙mol-1。
|
图 6 反应活化能的确定 (a) ln[Pu(IV)]o/ [Pu(IV)]o0与时间的关系,(b) ln(k')与1/T关系 Figure 6 Determination of activation energy. (a) Relationship between ln[Pu(IV)]o/ [Pu(IV)]o0 and time, (b) Relationship between ln(k') and1/T |
由式(8) 计算得出温度18 C时的k值,结果列于表 2。由一系列k取平均值,得出k=(8.50±0.41) × 10-2(mol∙L-1)1.4∙min-1。
| 表 2 k值的确定 Table 2 Determination of k. |
最终确定了硝酸肼还原反萃Pu(IV)动力学方程如下所示:
| $ - d{[Pu(IV)]_o}/dt = k{\left[ {Pu\left( {IV} \right)} \right]_o}{\left[ {HN{O_3}} \right]^{ - 1.9}}{\left[ {{N_2}{H_4}} \right]^{0.5}}$ | (11) |
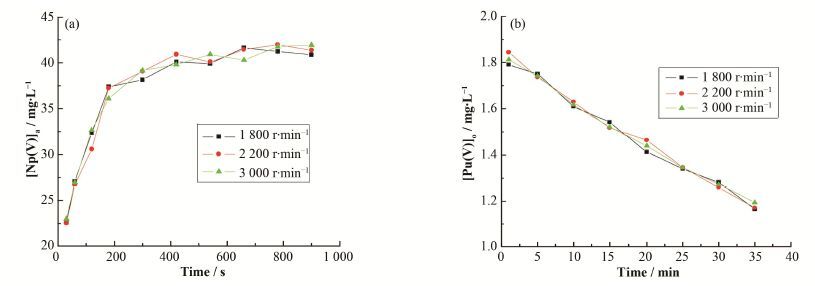
还原反萃过程涉及金属离子在两相间传质和金属离子氧化还原两个过程。搅拌速度是影响两相间传质过程的一个重要因素。因此,在T=20 C、[Pu(IV)]o0=1.9 mg∙L-1、[Np(VI)]o0=43 mg∙L-1、[HNO3]=1.0 mol∙L-1和[N2H4]=0.2 mol∙L-1条件下,考察了搅拌转速在1 800-3 000 r∙min-1搅拌转速对还原反萃过程的影响,结果如图 7所示。从图 7(a)和(b)中可以看出,在转速分别为1800 r∙min-1、2200r∙min-1和3 000 r∙min-1时,水相中Np(V)浓度和有机相中Pu(IV)浓度随时间变化的三条曲线几乎重合,表明转速对还原反萃过程无明显影响,即在高速搅拌的条件下,还原反萃过程的速控步骤主要为化学反应控制。
|
图 7 转速对还原反萃的影响 (a) [Np(V)]a与时间的关系,(b) [Pu(IV)]o与时间的关系 Figure 7 Effect of the rotational speed on the reductive stripping process. (a) Relationship between [Np(V)]a and time, (b) Relationship between [Pu(IV)]o and time |
依据硝酸肼还原反萃Np(VI)和Pu(IV)动力学方程,计算还原半反应时间,如表 3所示。表 3中τ50(Pu(IV))/τ50(Np(VI))的数值越高表明分离效果越好。从表 3可以看出,随着硝酸浓度、肼浓度以及温度的升高,τ50(Pu(IV))/τ50(Np(VI))的数值增加,Np(VI)/Pu(IV)的分离效果更好。其中,硝酸浓度和反应温度对Np(VI)/Pu(IV)的分离影响显著。
| 表 3 硝酸肼还原反萃Pu(IV)和Np(VI)的半反应时间 Table 3 Required time for 50% completion of Pu(IV) and Np(VI) reduction by hydrazine. |
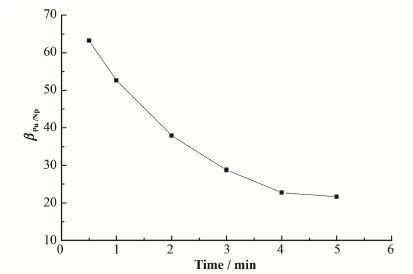
基于以上分析,结合所得动力学方程,模拟了硝酸肼分离Np(VI)和Pu(IV)的单级过程。图 8为硝酸浓度3 mol∙L-1、反应温度45 C、硝酸肼浓度0.1mol∙L-1条件下,分离系数
|
图 8 βPu/Np与反应时间的关系 Figure 8 Relationship between βPu/Np and time. |
| 表 4 Np(V)和Pu(III)百分比随时间的变化 Table 4 Variation of percentage of Np(V) and Pu(III) with time. |
本文研究了HNO3浓度、硝酸肼浓度、温度、转速对硝酸肼还原反萃有机相Np(VI)和Pu(IV)的过程,得出Np(VI)和Pu(IV)与硝酸肼的还原反萃动力学方程。研究表明,提高硝酸浓度、硝酸肼浓度和温度有助于Np(VI)/Pu(IV)分离,其中硝酸浓度和反应温度的影响显著。从分离系数βPu/Np与时间的关系可以看出,随着反应时间的延长,Np(VI)/Pu(IV)的分离效果变差。
| [1] |
Lange R G, Carroll W P. Review of recent advances of radioisotope power system[J].
Energy Conversion and Management, 2008, 49 (3) : 393 –401.
DOI: 10.1016/S0265-9646(99)00056-9 ( 0) 0)
|
| [2] |
Gunzo Uchiyama, Sachio Fujine, Shinobu Hotoku, et al. New separation process for neptunium, plutonium, and uranium using butyraldehydes as reductants in reprocessing[J].
Nuclear Technology, 1993, 102 : 341 –352.
DOI: 10.1016/j.enconman.2007.10.028 ( 0) 0)
|
| [3] |
尹东光, 张先业, 胡景炘, 等. 1, 1-二甲基肼应用于U、Np分离的研究[J].
核化学与放射化学, 1998, 20 (3) : 146 –151.
YIN Dongguang, ZHANG Xianye, HU Jingxin, et al. Separation of neptunium from uranium in contactor 1A with 1, 1-dimethylhydrazine[J]. Journal of Nuclear and Radiochemistry, 1998, 20 (3) : 146 –151. (  0) 0)
|
| [4] |
张希祥, 叶国安, 张先业, 等. 1, 1-二甲基肼还原Np(V)的动力学研究[J].
江汉大学学报(自然科学版), 2006, 34 (2) : 25 –27.
ZHANG Xixiang, YE Guoan, ZHANG Xianye, et al. Kinetic study of Np(V) reduction with 1, 1-dimethylhydrazine[J]. Journal of Jianghan University(Natural Science), 2006, 34 (2) : 25 –27. (  0) 0)
|
| [5] |
Yasutoshi Ban, Toshihide Asakura, Yasuji Morita. Reduction kinetics of Np(VI) by n-butyraldehydein tributyl phosphate diluted with n-dodecane[J].
Radiochimica Acta, 2004, 92 (12) : 883 .
DOI: 10.1524/ract.92.12.883.55113 ( 0) 0)
|
| [6] |
Yasutoshi Ban, Toshihide Asakura, Yasuji Morita.Separation of Np from U and Pu using a salt-free reductant for Np(VI) by continuous conter-current back-extraction[C].Global, 2005:371
( 0) 0)
|
| [7] |
张先业, 叶国安, 肖松涛, 等. 单甲基肼还原Np(VI)-I:反应动力学研究[J].
原子能科学技术, 1997, 31 (3) : 193 –198.
ZHANG Xianye, YE Guoan, XIAO Songtao, et al. Reduction of Np(VI) with monomethylhydrazine I:studies on reaction kinetics[J]. Atomic Energy Science and Technology, 1997, 31 (3) : 193 –198. (  0) 0)
|
| [8] |
张先业, 叶国安, 肖松涛, 等. 单甲基肼还原Np(VI)-II: Purex流程中U-Np分离的研究[J].
原子能科学技术, 1997, 31 (4) : 315 –320.
ZHANG Xianye, YE Guoan, XIAO Songtao, et al. Reduction of Np(VI) with monomethylhydrazine II:studies on partition of U-Np in Purex process[J]. Atomic Energy Science and Technology, 1997, 31 (4) : 315 –320. (  0) 0)
|
| [9] |
Srinivasan N, Ramaniah M V, Patil S K, et al. Estimation of neptunium in a fuel reprocessing plant[J].
Journal of Radioanalytical Chemistry, 1971, 8 : 223 –229.
DOI: 10.1007/BF02518186 ( 0) 0)
|
| [10] |
Koltunov V S, Tikhonov M F. Kinetics of reduction of neptunium by hydrazine II:reduction of Np(VI) to Np(V) in nitric acid[J].
Radiokhimiya, 1973, 15 : 194 –198.
( 0) 0)
|
| [11] |
李小该, 何辉, 叶国安, 等. 单甲基肼还原Np(V)的反应动力学[J].
核化学与放射化学, 2011, 33 (1) : 1 –5.
LI Xiaogai, HE Hui, YE Guoan, et al. Kinetics of reaction between methylhydrazine and neptunium(V)[J]. Journal of Nuclear and Radiochemistry, 2011, 33 (1) : 1 –5. (  0) 0)
|
| [12] |
肖松涛, 叶国安, 欧阳应根, 等. 羟胺乙酸与Pu(IV)的还原动力学[J].
原子能科学技术, 2009, 43 (5) : 400 –405.
XIAO Songtao, YE Guoan, OUYANG Yinggen, et al. Kinetics of reaction between Pu(IV) and(hydroxyamino) acetic acid in nitric acid solution[J]. Atomic Energy Science and Technology, 2009, 43 (5) : 400 –405. (  0) 0)
|


