2. 中国科学院大学 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
球床堆由于结构复杂不利于几何建模,因此在计算流体动力学(Computational Fluid Dynamics, CFD)模拟中多采用多孔介质来等效球床区域[1-3]。即将多孔区域视作连续相,来求解流场和温度场,并分别使用附加阻力压降公式和对流换热公式修正对应的动量和能量方程[4]。早期计算多孔介质区域的附加阻力压降主流公式有层流Darcy公式和湍流Ergun公式,计算对流换热Nu主要使用Wakao公式[4-7]。为了验证这些已有公式用于球床堆模拟的有效性,诸多研究人员进行了大量研究。
目前,使用了球形燃料的核反应堆主要有气冷堆和固态燃料熔盐堆[8]。德国研究机构基于其研究开发的氦气冷却的高温堆,拟合了有别于上述公式的KTA(Kerntechnischer Ausschuss, 德国研究机构)压降公式和KTA对流换热Nu公式[9-10]。熔盐堆由于缺乏实验数据,目前还没有统一的计算公式。宋世雄[8]使用RNG(Re-Normalization Group, 重整化群)k-e湍流模型对3cm直径燃料球的氟盐冷却高温堆(Pebble Bed-Advanced High-Temperature Reactor, PB-AHTR)进行了CFD模拟,拟合了压降公式和对流换热Nu公式。此外,孟现珂等[1]根据真实实验得到了水流在毫米级颗粒球床中的压降和对流换热结果,并拟合了相应的公式。
中国科学院上海应用物理研究所设计了10MW固态燃料熔盐堆(Thorium Molten Salt Reactor-Solid Fuel V1, TMSR-SF1)采用6cm直径的固态燃料球随机填充堆芯,以液态FLiBe盐作为堆芯冷却剂[11-13]。本文将使用Ansys Fluent14.5软件基于TMSR-SF1建立规则球床模型,使用Re适用范围更宽的SST-4eq湍流模型计算熔盐流动的压降和对流换热系数,以验证上述多孔介质模型的公式在熔盐冷却球床堆中的有效性,并基于模拟结果对上述公式进行必要的拟合修正,最后将得到的修正公式用于其它直径小球的球床中验证适用性。
1 研究方法 1.1 多孔介质模型利用CFD研究流动和换热,当求解域为多孔介质时,质量、动量和能量守恒方程里的物性参数和物理量是对多孔区域内采用体积平均化处理后的结果。其中最主要的平均化物理量有孔隙率ε和表观速度u:
| $ u=\dot m/\left({\rho A} \right) $ | (1) |
式中:
多孔介质模型常用的阻力因子和对流换热Nu表达式和压降公式如下:
| $ {S_{i, {\mathop{\rm KTA}\nolimits} }}=-\left({\frac{{320}}{{\left({\frac{{Re}}{{1-\varepsilon }}} \right)}}+\frac{6}{{{{\left({\frac{{Re}}{{1-\varepsilon }}} \right)}^{0.1}}}}} \right)\frac{{1-\varepsilon }}{{{\varepsilon ^3}}}\frac{1}{{{d_{\mathop{\rm P}\nolimits} }}}\frac{\rho }{2}\left| u \right|{u_i} $ | (2) |
| $ {S_{i, {\mathop{\rm Ergun}\nolimits} }}=-[150\frac{{{{\left({1-\varepsilon } \right)}^2}\mu }}{{{\varepsilon ^3}{d_P}^2}}{u_i}+1.75\frac{{\left({1-\varepsilon } \right)\rho }}{{{\varepsilon ^3}{d_{\mathop{\rm P}\nolimits} }}}\left| u \right|{u_i}] $ | (3) |
对流换热Nu公式为:
| $ N{u_{{\mathop{\rm KTA}\nolimits} }}=1.27\frac{{P{r^{1/3}}}}{{{\varepsilon ^{1.18}}}}R{e^{0.36}}+0.033\frac{{P{r^{1/2}}}}{{{\varepsilon ^{1.07}}}}R{e^{0.86}} $ | (4) |
| $ N{u_{{\mathop{\rm Wakao}\nolimits} }}=2+1.1P{r^{1/3}}R{e^{0.6}} $ | (5) |
式中:Si为i方向附加线性阻力,Pa·m-1;ui为i方向表观流速,m·s-1;e为球床孔隙率,e=Vvoid/Vbed;Vvoid、Vbed分别为孔隙体积和球床总体积,m3;dP为填充球床的燃料球直径,m;Re和Nu的特征长度取dP;Re的特征速度取表观速度u。
在Fluent程序中,多孔介质模型主要使用二次方阻力(Ergun方程)或幂律阻力计算附加阻力[14]。对于能量方程,采用非平衡模型,即固相和流体介质间存在温差,两相间的能量传递由傅立叶冷却公式计算。因此,阻力系数和对流换热系数都是需要输入的边界条件。
1.2 直接CFD球床模型直接CFD模型利用Fluent程序建立球床真实的几何模型,模拟球床中流动与换热,求解熔盐在规则球床中的压降和对流换热系数,对上述多孔介质模型公式中的常数系数进行修正,为球床的等效多孔介质模型提供参考依据。
2 模型建立与计算在CFD模拟中,对计算结果准确性有直接影响的包括几何建模、网格划分、边界条件、湍流模型和迭代求解器等步骤。
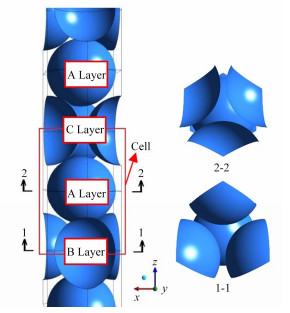
2.1 几何建模与网格划分本文使用了规则堆积球床模型如图 1所示,使用ABACABAC…的循环排列,改型自面心立方排列(ABCABC…循环),理论最大填充率约为74.01%[4-5]。该排列具有基本对称cell的体积较小、且无直通孔的优点。
|
图 1 规则球床模型示意图 Figure 1 Schematic of the pebble bed arranged in order. |
由图 1,该模型包括11个以A层为中心的基本cell,以消除进出口效应的影响。小球直径60mm,球心间距64mm,孔隙率40%,与TMSR-SF1堆芯孔隙率一致。对于球间相对位置区域的处理方法有增加球间距、扁平化处理和小圆柱桥接,本研究采用增加球间距的处理方法[15]。
图 2为局部网格示意图,经网格无关性验证,网格数量1.1516×107,最差网格质量0.444,相关数据如表 1所示。

|
图 2 规则球床球间局部网格示意图 Figure 2 Schematic of the bed grid. |
| 表 1 网格无关性验证相关数据 Table 1 Data of grid-independent verification. |
对于cell内的平均线性压降,取cell上、下截面平均压力的差值作为压差,计算如式(6):
| $ \frac{{\Delta P}}{L}=\frac{{{P_1}-{P_2}}}{L} $ | (6) |
式中:P 1为cell进口压力,Pa;P 2为cell出口压力,Pa;L为cell在流向方向长度,m。
对于cell内的平均Nu数,计算如式(7):
| $ h=\frac{q}{{{{\bar T}_w}-{{\bar T}_f}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt}, {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} Nu=\frac{{h \cdot {d_{\mathop{\rm P}\nolimits} }}}{\lambda } $ | (7) |
式中:q为球壳壁面热流密度,W∙m-2;Tw为cell内球壳平均温度,℃;Tf为cell内流体的平均温度,℃。
2.2 边界条件熔盐物性主要包括密度、粘度、热容和热导率等,参考TMSR-SF1设计资料,暂不考虑变物性的影响[13]。具体参数为:密度ρ=1986 kg·m-3;动力粘度μ=0.00855Pa·s;定压热容c=2390 J∙(kg∙K)-1;热导率λ=1.1 W∙(m∙K)-1。
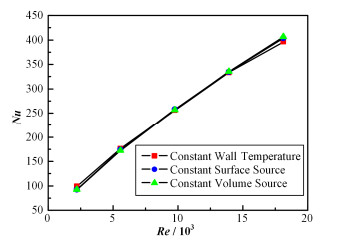
为简化计算,模型中不考虑球体内部,采用球壳均匀热流密度模型[16]。为验证改变热边界条件带来的影响,模拟并比较了绕流单球的均匀体热源、球壳均匀热流和球壳恒温,如图 3所示。
|
图 3 绕流单球对流换热模拟结果 Figure 3 Simulation result of the flow past single sphere. |
由图 3,三种绕流单球的对流换热模拟表明:同等热功率条件下,球壳均匀热流模型与均匀体热源模型得到的对流换热系数相对较接近。
2.3 湍流模型对于球床模拟的湍流模型,Shams等[17-18]针对气冷堆的系列研究指出,直接模拟(Direct Numerical Simulation, DNS)优于大涡模拟(Large Eddy Simulation, LES),此两种模型均可以获得高精度解,但需要耗费巨大的机时,而稳态的SST模型耗时少,也能满足计算精度要求,因此对球床的模拟计算选择SST模型。
根据Fluent帮助文件,建议在使用SST模型时,壁面附近的第一层网格Y-Plus应小于8,小于1最佳,且增长率应小于1.1[14]。本文建立的模型在模拟的最大Re数3500时,壁面附近Y-Plus最大值为1.5,出现在入口区域,堆芯区域Y-Plus均小于1,符合计算要求。
3 计算结果 3.1 规则球床氦气流动与换热模拟结果在进行球床熔盐流动与换热模拟前,为了验证CFD模拟球床流动压降和换热结果的可靠性,对比了规则球床气体流动实验结果,表 2为氦气模拟结果,作为对比给出了杨剑等[19]基于FCC排列球床空气流动实验数据。
| 表 2 规则球床氦气模拟结果 Table 2 Result of the CFD simulation on helium. |
由表 2,压降模拟结果偏差较大,高达40%-50%;而Nu偏差较小,不超过15%。杨剑[19]的CFD模拟结果表现出与上述类似的偏差,他将其解释为实验中球间接触排列理论上会增加阻力系数,但对换热影响不大。综合结果表明,本研究中CFD模型用于球床的压降与换热计算具有可行性。
3.2 规则球床熔盐流动与换热模拟结果球床熔盐流动与换热模拟选取Re范围在200-3500,涵盖了TMSR-SF1堆芯所有可能的实际工况。残差维持稳定,迭代次数在15000次左右。使用10个CPU和1个GPU并行计算,每个case实际耗时约90h。
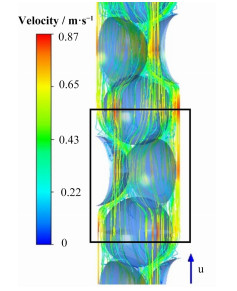
图 4、5为Re=1700时,第6个cell的A层的中心小球附近的流线图和小球壁面的温度场云图。
|
图 4 球床中熔盐流动流线图 Figure 4 Streamline of salt flow in packed bed. |
|
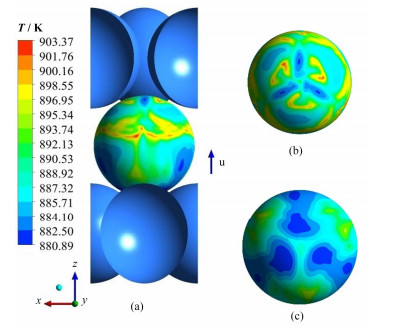
图 5 球面温度云图(a)、远端(b)和近端(c) Figure 5 Temperature contours of sphere surface (a), rear (b) and front (c). |
由图 4,在cell内出现了平直的z方向流线,表明流体在连续两个中心A层间的局部通孔出现了直流,相对于复杂的随机球床,该现象会降低流动阻力。在两球相对的区域,流线密集,颜色加深,表明熔盐出现加速,强化了熔盐与球壳的对流换热。但在真实球床中,相邻小球相切接触,会存在滞留区导致传热恶化,这也是CFD球床模拟与实际球床的差异。
图 5中的球壳表面温度场与流体绕流单球的温度场相似,迎流区以及靠近迎流区的球间狭窄区域温度较低,而背流区以及靠近背流区的球间狭窄区域出现了局部热点。
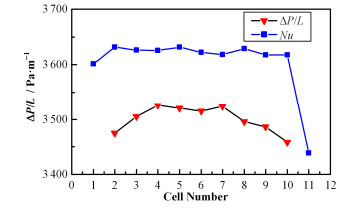
图 6为各单元单位内单位长度的平均压降和各单元内的平均Nu数。
|
图 6 各cell内的线性压降和Nu数 Figure 6 Average of linear pressure drop and Nusselt numbers. |
图 6中压降和对流换热Nu数明显受进出口效应影响,去除进、出口附近的各三个单元,选择4-7号cell算术平均结果计算得到线性压降和对流换热Nu。
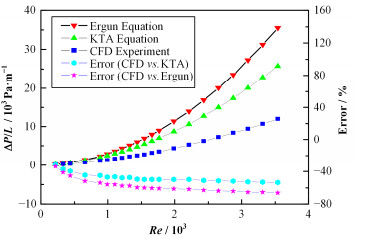
3.3 熔盐流动模拟结果与已有公式对比计算得到的有效段压降曲线和对流换热Nu数曲线分别如图 7、8所示。
|
图 7 规则球床中熔盐流动压降模拟结果 Figure 7 Pressure drop of molten salt flow in packed bed. |
由图 7可知,压降计算结果与Ergun公式和KTA公式相比明显偏小,且Re越大,偏差越大。其中,与Ergun公式的偏差从30%逐渐增加到60%,而与KTA公式的偏差稳定在50%。
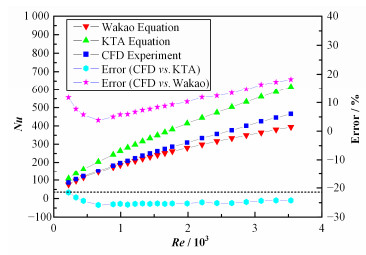
由图 8,Nu随Re的变化趋势与Wakao公式给出的值较吻合,差异在10%-20%之间;而与KTA对流换热公式给出的预测值差异较大,但基本都维持在25%左右。
|
图 8 规则球床中熔盐流动对流换热模拟结果 Figure 8 Convection of molten salt flow in packed bed. |
基于上述模拟结果,对已有公式进行拟合修正,压降和对流换热Nu都分别得到了两种拟合形式。在拟合压降公式时,依据已有的文献[20-21],对公式进行无量纲化,针对常数系数进行修正,分别对KTA和Ergun压降形式处理:
| $ {}^{\frac{Re}{1-\varepsilon }\cdot {{S}_{i,\text{KTA}}}}\!\!\diagup\!\!{}_{\frac{1-\varepsilon }{{{\varepsilon }^{3}}}\frac{1}{{{d}_{\operatorname{P}}}}\frac{\rho }{2}\left| u \right|{{u}_{i}}}\;=A+B\cdot {{\left( \frac{Re}{1-\varepsilon } \right)}^{0.9}} $ | (8) |
| $ \begin{align} & {}^{{{S}_{i,\text{Ergun}}}}\!\!\diagup\!\!{}_{\frac{\rho {{u}^{2}}}{{{d}_{\operatorname{P}}}}}\;={{C}_{1}}\frac{{{\left( 1-\varepsilon \right)}^{2}}}{{{\varepsilon }^{3}}}\frac{1}{Re}+{{C}_{2}}\frac{\left( 1-\varepsilon \right)}{{{\varepsilon }^{3}}} \\ & =B\cdot \frac{1}{Re}+A \end{align} $ | (9) |
将式(8)和(9)稍作转换,拟合求解斜率B和截距A。Nu公式也做类似处理,得到拟合修正公式(10)-(13)。
KTA压降修正:
| $ \frac{{\Delta {P_i}}}{L}=\left({\frac{{598.4}}{{\frac{{Re}}{{1-\varepsilon }}}}+\frac{{2.65}}{{{{\left({\frac{{Re}}{{1-\varepsilon }}} \right)}^{0.1}}}}} \right)\frac{{1-\varepsilon }}{{{\varepsilon ^3}}}\frac{1}{D}\frac{\rho }{2}\left| u \right|{u_i} $ | (10) |
Ergun压降修正:
| $ \frac{{\Delta {P_i}}}{L}=436.5\frac{{{{\left({1-\varepsilon } \right)}^2}\mu }}{{{\varepsilon ^3}{d_{\mathop{\rm P}\nolimits} }^2}}{u_i}+0.54\frac{{\left({1-\varepsilon } \right)\rho }}{{{\varepsilon ^3}{d_{\mathop{\rm P}\nolimits} }}}\left| u \right|{u_i} $ | (11) |
Wakao对流换热修正:
| $ Nu=20+0.44R{e^{0.73}}P{r^{{\rm{1/3}}}} $ | (12) |
KTA对流换热修正:
| $ Nu=0.95\frac{{P{r^{1/3}}}}{{{\varepsilon ^{1.18}}}}R{e^{0.36}}+0.025\frac{{P{r^{1/2}}}}{{{\varepsilon ^{1.07}}}}R{e^{0.86}} $ | (13) |
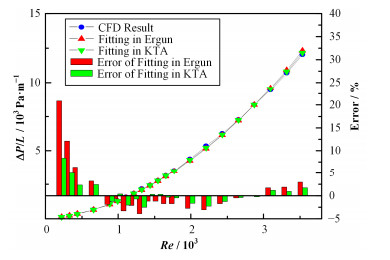
|
图 9 规则球床熔盐流动模拟压降拟合误差 Figure 9 Fitting error of the pressure drop curve for salt flow. |
|
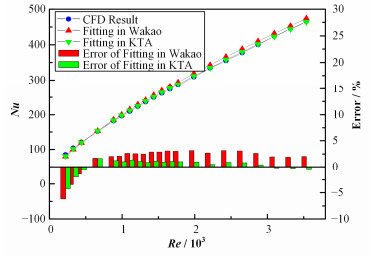
图 10 规则球床熔盐对流换热拟合误差 Figure 10 Fitting error of the convention curve for salt flow. |
由图 9,KTA形式的拟合误差较平稳,且小于Ergun形式的拟合误差。Ergun和KTA公式等号右边第一项为粘性项,即由流体的粘性引起的压降;第二项为惯性项,主要是由球床几何形状造成的压降。对比拟合公式和原公式均可以发现,本文拟合得到的公式增加了粘性压降,而减小了惯性压降。分析原因,可能是由于熔盐粘度较大,而规则球床形阻小,因此,惯性压降贡献相对减小。
由图 10,Wakao修正在低Re段拟合误差较大。当Re趋于0时,对流换热Nu趋近于一个非零常数,得到Wakao等诸多学者的实验验证。而另一部分学者则认为Nu应随Re趋于0,对流换热公式不应有常数存在,因为对流产生于流体的宏观运动,实验中的常数是由于扩散导致[7]。
3.4 拟合公式在3cm小球的规则球床适用性验证在Fluent中模拟计算小球直径30mm时,熔盐流场的压降与对流换热。图 11为30mm直径小球的球床中,分别使用拟合公式计算得到的结果和模拟结果。
|
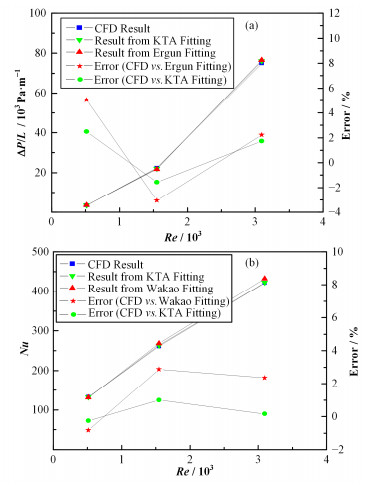
图 11 熔盐在30mm直径小球的球床流动模拟结果 (a)压降模拟结果,(b)对流换热模拟结果 Figure 11 Simulation results of salt flow in bed packed by sphere in 30-mm diameter. (a) Pressure drop result, (b) Heat transfer result |
图 11的结果表明,模拟结果与两种形式的拟合公式误差都较小,但KTA形式拟合修正得到的压降和对流换热公式误差相对更小,建议采用KTA拟合修正公式。因此,拟合公式理论上可用于30-60 mm小球的60%填充率的规则球床。
4 结语本文对类密排六方堆积的规则球床进行了建模计算,并对网格模型、边界条件和湍流模型进行了必要的验证模拟。最终模拟得到的熔盐在规则球床内流动的平均阻力压降和平均对流换热Nu,结论如下:
1)以熔盐为工质的阻力压降模拟结果均大于Ergun或KTA压降公式的预测值。
2)以熔盐为工质的对流换热Nu模拟结果与Wakao对流换热公式预测值较接近,与KTA对流换热公式的预测值相差25%左右。
3)基于模拟结果对原有公式修正,分别得到了如KTA和Ergun形式的压降公式,通过误差分析,推荐使用KTA形式拟合修正公式:
| $ \frac{{\Delta {P_i}}}{L}=\left({\frac{{598.4}}{{\frac{{Re}}{{1-\varepsilon }}}}+\frac{{2.65}}{{{{\left({\frac{{Re}}{{1-\varepsilon }}} \right)}^{0.1}}}}} \right)\frac{{1-\varepsilon }}{{{\varepsilon ^3}}}\frac{1}{D}\frac{\rho }{2}\left| u \right|{u_i} $ | (14) |
4)基于模拟结果对原有公式修正,分别得到了如KTA和Wakao形式的对流换热Nu数关系式,通过误差分析,推荐使用KTA形式拟合修正公式:
| $ Nu=0.95\frac{{P{r^{1/3}}}}{{{\varepsilon ^{1.18}}}}R{e^{0.36}}+0.025\frac{{P{r^{1/2}}}}{{{\varepsilon ^{1.07}}}}R{e^{0.86}} $ | (15) |
5)熔盐在30mm球的规则球床中的流动与换热的计算结果与拟合修正公式结果较吻合。
| [1] |
Meng X K, Sun Z N, Xu G Z, et al. Single-phase convection heat transfer characteristic of the pebble-bed channels with internal heat generation[J].
Nuclear Engineer and Design, 2012, 252 (10) : 121 –127.
DOI: 10.1016/j.nucengdes.2012.05.041 ( 0) 0)
|
| [2] |
Bardet P, Blandford E, Fratoni M, et al. Design, analysis and development of the modular PB-AHTR[R]. Berkeley, CA, USA:University of California, 2008
( 0) 0)
|
| [3] |
Scarlat R. Pebble bed heat transfer-particle-to-fluid heat convection[R]. Berkeley, CA, USA:University of California, 2009
( 0) 0)
|
| [4] |
Bear J.
Dynamics of fluids in porous media[M]. New York, USA: American Elsevier Publishing Company INC, 1972 .
( 0) 0)
|
| [5] |
Scheidegger A E.
The physics of flow through porous media[M]. Toronto, Japan: University of Toronto Press, 1974 .
( 0) 0)
|
| [6] |
Ergun S. Fluid flow through packed columns[J].
Chemical Engineering Progress, 1952, 48 (2) : 89 –94.
( 0) 0)
|
| [7] |
Wakao N, Kaguei S.
Heat and mass transfer in packed beds[M]. New York, USA: Gordon and Breach Science Publishers, 1982 .
( 0) 0)
|
| [8] |
Song S, Cai X, Liu Y, et al. Pore scale thermal hydraulics investigations of molten salt cooled pebble bed high temperature reactor with BCC and FCC configurations[J].
Science & Technology of Nuclear Installations, 2014, 3 : 1 –16.
DOI: 10.1155/2014/589895 ( 0) 0)
|
| [9] |
Geschäftsstelle des Kerntechnischen Ausschusses. KTA 3102.3, reactor core design of high-temperature gas-cooled reactors Part 3:loss of pressure through friction in pebble bed cores[R]. Berlin, Germany:Nuclear Safety Standards Commission, 1981
( 0) 0)
|
| [10] |
Geschäftsstelle des Kerntechnischen Ausschusses. KTA 3102.2, reactor core design of high-temperature gas-cooled reactors Part 2:heat transfer in spherical fuel elements[R]. Berlin, Germany:Nuclear Safety Standards Commission, 1983
( 0) 0)
|
| [11] |
江绵恒, 徐洪杰, 戴志敏. 未来先进核裂变能--TMSR核能系统[J].
中国科学院院刊, 2012, 27 (3) : 366 –374.
DOI: 10.3969/j.issn.1000-3045.2012.03.016 JIANG Mianheng, XU Hongjie, DAI Zhimin. Advanced fission energy program-TMSR nuclear energy system[J]. Bulletin of Chinese Academy of Sciences, 2012, 27 (3) : 366 –374. DOI: 10.3969/j.issn.1000-3045.2012.03.016 (  0) 0)
|
| [12] |
牛强, 宋士雄, 魏权, 等. 熔盐冷却球床堆热通道热工水力特性数值分析[J].
核技术, 2014, 37 (7) : 070602 .
DOI: 10.11889/j.0253-3219.2014.hjs.37.070602 NIU Qiang, SONG Shixiong, WEI Quan, et al. Thermal-hydraulics numerical analyses of pebble bed advanced high temperature reactor hot channel[J]. Nuclear Techniques, 2014, 37 (7) : 070602 . DOI: 10.11889/j.0253-3219.2014.hjs.37.070602 (  0) 0)
|
| [13] |
梅牡丹, 邵世威, 何兆忠, 等. 固态钍基熔盐堆概率安全评价始发事件分析研究[J].
核技术, 2014, 37 (9) : 090601 .
DOI: 10.11889/j.0253-3219.2014.hjs.37.090601 MEI Mudan, SHAO Shiwei, HE Zhaozhong, et al. Research on initial event analysis for solid thorium molten salt reactor probabilistic safety assessment[J]. Nuclear Techniques, 2014, 37 (9) : 090601 . DOI: 10.11889/j.0253-3219.2014.hjs.37.090601 (  0) 0)
|
| [14] |
ANSYS Inc. ANSYS FLUENT theory guide[OL]. Release 15.0, 2013. https://uiuc-cse.github.io/me498cmfa15/lessons/fluent/refs/ANSYS%20Fluent%20Theory%20Guide.pdf
( 0) 0)
|
| [15] |
徐广展, 孙中宁, 孟现珂, 等. 球床堆流动与传热数值模拟[J].
核动力工程, 2013, 34 (3) : 63 –66.
XU Guangzhan, SUN Zhongning, MENG Xianke, et al. Numerical simulation of fluid flow and heat transfer in pebble bed reactor[J]. Nuclear Power Engineering, 2013, 34 (3) : 63 –66. (  0) 0)
|
| [16] |
杨世铭, 陶文铨.
传热学[M]. 北京: 高等教育出版社, 2006 .
YANG Shiming, TAO Wenquan. Heat transfer[M]. Beijing: Higher Education Press, 2006 . (  0) 0)
|
| [17] |
Shams A, Roelofs F, Komen E M J, et al. Quasi-direct numerical simulation of a pebble bed configuration[J].
Nuclear Engineering & Design, 2013, 263 (1) : 473 –489.
DOI: 10.1016/j.nucengdes.2012.06.016 ( 0) 0)
|
| [18] |
Shams A, Roelofs F, Komen E M J, et al. Large eddy simulation of a nuclear pebble bed configuration[J].
Nuclear Engineering & Design, 2013, 261 (8) : 10 –19.
DOI: 10.1016/j.compfluid.2014.03.025 ( 0) 0)
|
| [19] |
Yang J, Wang J, Bu S, et al. Experimental analysis of forced convective heat transfer in novel structured packed beds of particles[J].
Chemical Engineering Science, 2012, 71 (13) : 126 –137.
DOI: 10.1016/j.ces.2011.12.005 ( 0) 0)
|
| [20] |
Zuo J X, Jing J P, Bi J S, et al. Framework analysis of fluoride salt-cooled high temperature reactor probabilistic safety assessment[J].
Nuclear Science and Techniques, 2015, 26 (5) : 050602 .
DOI: 10.13538/j.1001-8042/nst.26.050602 ( 0) 0)
|
| [21] |
杨群, 于世和, 邹杨, 等. 氟盐冷却球床堆与HTR-10和MSRE的定量相似性分析[J].
核技术, 2016, 39 (1) : 010601 .
DOI: 10.11889/j.0253-3219.2016.hjs.39.010601 YANG Qun, YU Shihe, ZOU Yang, et al. Quantitative similarity analysis of the fluoride salt-cooled pebble bed reactor with HTR-10 and MSRE[J]. Nuclear Techniques, 2016, 39 (1) : 010601 . DOI: 10.11889/j.0253-3219.2016.hjs.39.010601 (  0) 0)
|


