2. 中国科学技术大学 核科学技术学院 合肥 230026
2. School of Nuclear Science and Technology, University of Science and Technology of China, Hefei 230026, China
将计算流体动力学(Computational Fluid Dynamics, CFD)应用于流量分配的研究可以缩短设计周期,减少实验成本。尽管计算机技术的进步极大地推广了CFD方法的应用,但是针对完整组件或者反应堆堆芯的流量分配研究,仍然受到计算资源的制约。
板状燃料元件因为其良好的传热特性,而被广泛应用于研究堆中[1-6]。在板状燃料组件中,冷却剂通道不再是由棒束组成的开式通道,而是由燃料板及相关支撑结构组成的闭式流道。同时,为了提高通道内冷却剂的雷诺数,增强换热效果,燃料板间隙通常很小,使得流道尺寸变得狭长。针对板状燃料组件冷却剂通道这种特殊的几何特征,本文在原有CFD方法上进行改进,减小对计算资源的需求,使CFD方法在板状燃料组件的流量分配研究中得到推广。
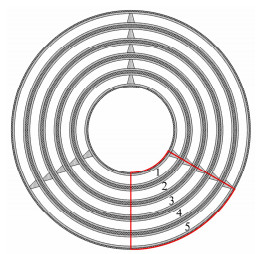
1 研究对象选取由中国核动力研究设计院设计的多层环形板状燃料组件为研究对象[7-11],如图 1所示。该组件的冷却剂为轻水,工作压力2MPa,入口温度318.15K。所有流道在径向的宽度均为2mm,流动方向长度均为1110mm。流道中间燃料板厚度为1.5mm,最内侧流道内径为21mm,最外侧流道外径为53mm。由于计算对象几何上的对称性,计算域选取为整个组件的1/6,即图 1中线框所示区域,以减小计算域的规模。从内到外,分别将5个流道命名为流道1、流道2、……、流道5。由于流量分配的实验多为冷态实验[12],故计算过程中不考虑燃料板的发热,因此可以省略燃料板,仅对流道区域进行建模。
|
图 1 燃料组件横截面 Figure 1 Cross-sectional view of the assembly. |
分别使用两种CFD方法对板状燃料组件的流量分配进行研究,即传统的完整建模直接求解方法和本文新提出的部分建模迭代求解方法。
2.1 完整建模直接求解对板状燃料组件进行完整建模,并将CFD方法直接应用于其流量分配的研究需要庞大的计算资源,为了解释其原因,需要引入湍流CFD计算中一个重要的无量纲参数y+,其定义如下:
| ${{y}^{+}}=\frac{{{u}_{\tau }}y}{\nu }$ | (1) |
式中:ut是近壁第一个流体网格的摩擦速度;y是该网格中心距壁面的距离;v是流体的运动粘度。
首先,对于板状燃料组件而言,冷却剂流速快,第一个网格处的摩擦速度也相应较大,对于特定的y+,第一个网格距壁面的距离就需要相应的减小。
其次,对于流量分配的研究而言,各流道进出口局部阻力的精确计算是至关重要的。因此标准化壁面函数等(理论上要求y+ > 30)针对于充分发展湍流边界层建立的处理方式并不是最佳的选择,而应该使用能够考虑边界层粘性底层的近壁面处理方式,无论是低雷诺数模型还是使用增强型壁面处理均要求y+≈1。该准则将导致第一层网格尺寸明显减小。
再次,近壁面网格尺寸的减小会导致网格数量的急剧上升。从网格尺寸变化率的角度考虑,各流动截面的网格都需要划分的更稠密来降低近壁面附近的网格尺寸变化率。从网格长宽比的角度考虑,单个流动截面上网格尺寸的减小,将导致流动方向需要的网格数量增多。对于狭长的冷却剂流道而言,在流动方向上增加的网格数量将是相当可观的。
2.2 部分建模迭代求解板状燃料组件的冷却剂流道虽然狭长,但是其中的冷却剂通道却是闭式流道,即各通道间不存在冷却剂的交混,这一特性为简化板状燃料组件CFD研究提供了可能。冷却剂通道狭长,使得每个流道除出、入口段之外的大部分流道内的冷却剂流动是接近充分发展的。前已述及,由于近壁面网格尺寸变小与网格递增速率及网格长宽比的限制,各流道内网格数量是相当庞大的,但这些网格求解的流动并不复杂,因此若能简化流道内接近充分发展区域的计算,则可以大幅度减小CFD研究对计算资源的需求。
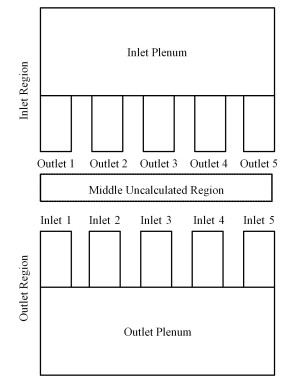
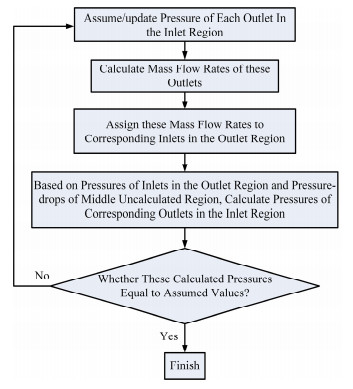
具体到本文的计算对象而言,如图 2所示,认为中间部分流道内流动是充分发展的,建模时将入口腔室和与其相连的一部分流道定义为入口部分,将出口腔室和与其相连的一部分流道定义为出口部分。建模过程中,计算了5个流道当量直径的平均值为3.77mm,入口部分及出口部分流道长度均取为该平均长度的10倍,即37.7mm。求解过程如图 3所示,通过入口部分各出口压力的迭代计算,实现由部分模型计算整个计算域流量分配的功能。
|
图 2 部分建模示意图 Figure 2 Schematic view of partial modeling. |
|
图 3 部分建模迭代求解流程 Figure 3 Iteration of partial modeling process. |
迭代计算过程中,各流道的流量是动态变化的,因此中间未计算部分的压降也是变化的,需要根据各流道流量计算出各中间未计算部分的压降,进而修正入口部分各出口处的压力。但是,对于不规则形状的流道,中间未计算部分压降与流量的关系是未知的,亦需要通过CFD方法获取。具体实现上可以分为两种方式:一种是根据每次的流量计算值,直接通过CFD方法计算相应的压降值;另一种方式是事先通过CFD方式获得各流道压降与流量的关系式,在流量分配的迭代计算过程中通过调用关系式的方式获取动态变化的压降值。显然,第一种方法会更为准确,但是明显地增多计算量;而第二种方法则相对简单,利用经验关系式计算沿程阻力也是工程上常用的方法,通过较多数据点的拟合,即可获得精度较高的压降与流量的关系式。
为了提高迭代计算的效率,本文选取了第二种方式来计算中间未计算段的压降。其具体步骤为:选取一段长度(计算中为4mm)的流道区域,将各流道的出入口分别设置为周期性边界条件,调整计算域的压降梯度,得出各流道相应的流量,最后拟合出沿程阻力系数的关系式。
在计算的过程中,本文的压降梯度从300000-500000 Pa·m-1均匀地选取了9个数值,参照Blasius关系式的形式,拟合得到了各流道阻力系数与雷诺数的关系式见表 1。
| 表 1 阻力系数与雷诺数拟合关系式 Table 1 Fitted formulas of l and Re. |
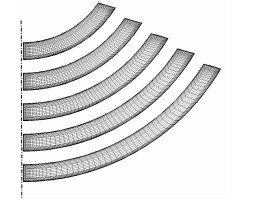
由于计算域结构较规则,选择结构化的网格划分方式。各流道进行O网格划分,减小网格数量的同时保证了网格质量。选取各冷区间通道的流量作为网格独立性检验的标准,无流量分配组件、完整建模时进行网格独立性检验的结果表明,节点数为11737645的网格各流道流量与节点数为7220152的网格计算值,最大偏差为0.4‰,考虑到计算资源的限制,本文不再扩大计算规模。同时考虑到流量为本研究所关注的重点,将11737645节点数网格选为完整建模方法使用的网格。最终选用网格的流道细节如图 4所示。部分建模是对流道即腔室的网格进行了相应的加密,最后选取的网格包含3011768个节点。
|
图 4 流道截面网格 Figure 4 Cross-sectional view of the mesh. |
本文选取Realizable k-ε两方程模型进行湍流的相关求解,其对标准k-ε两方程模型进行了修正,使其应用范围更加广泛。其中,关于湍动能k和湍动能耗散率ε的控制方程如下[13]:
| $\begin{array}{l} \left\{ \begin{array}{l} \frac{\partial }{{\partial t}}(\rho k) + \frac{\partial }{{\partial {x_j}}}(\rho k{u_j}) = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _k}}}} \right)\frac{{\partial k}}{{\partial {x_j}}}} \right] + \\ \quad \quad \begin{array}{*{20}{c}} {}&{}&{} \end{array}\begin{array}{*{20}{c}} {}&{}&{} \end{array}\begin{array}{*{20}{c}} {} \end{array}{G_k} + {G_b} - \rho \varepsilon - {Y_M} - {S_k}\\ \frac{\partial }{{\partial t}}(\rho \varepsilon ) + \frac{\partial }{{\partial {x_j}}}(\rho \varepsilon {u_j}) = \frac{\partial }{{\partial {x_j}}}\left[ {\left( {\mu + \frac{{{\mu _t}}}{{{\sigma _\varepsilon }}}} \right)\frac{{\partial \varepsilon }}{{\partial {x_j}}}} \right] + \\ \quad \quad \begin{array}{*{20}{c}} {}&{}&{} \end{array}\begin{array}{*{20}{c}} {}&{}&{} \end{array}\begin{array}{*{20}{c}} {} \end{array}\rho {C_1}S\varepsilon - \rho {C_2}\frac{{{\varepsilon ^2}}}{{k + \sqrt {\nu \varepsilon } }} + \\ \begin{array}{*{20}{c}} {}&{}&{} \end{array}\begin{array}{*{20}{c}} {}&{}&{} \end{array}\begin{array}{*{20}{c}} {\begin{array}{*{20}{c}} {} \end{array}} \end{array}\begin{array}{*{20}{c}} {}&{} \end{array}{C_{1\varepsilon }}\frac{\varepsilon }{k}{C_{3\varepsilon }}{G_b} + {S_\varepsilon } \end{array} \right.\\ {C_1} = \max \left[ {0.43,\frac{\eta }{{\eta + 5}}} \right],\eta = S\frac{k}{\varepsilon },S = \sqrt {2{S_{ij}}{S_{ij}}} \end{array}$ | (2) |
式中:Gk表示由于平均速度梯度而产生的湍流动能项;Gb表示由于浮生力产生的湍流动能项;YM表示可压缩湍流中脉动膨胀对整体湍流扩散率的贡献;C2和C1ε是常数;σk和σε分别是k和ε的湍流普朗特数;Sk和Sε是源项。近壁面的区域使用增强型壁面处理。流道区域以面积加权的y+平均值为1.04,满足直接求解近壁面区域y+≈1的要求。
3 计算结果与讨论本文分别利用两种计算方法计算了两种工况下的流量分配情况:一种是认为腔室内不存在流量分配组件,冷却剂直接进入流道;另一种是认为入口腔室内存在流量分配组件,但不模拟组件的具体形状,参照文献[9-10]中的处理方式,人为地在各流道入口处添加阻力源项来模拟组件对流量分配的影响,其具体的多孔跳跃常数见表 2。在给定流量分配组件形状时,可以进行精细建模,发挥CFD的优势,充分考虑其对流场细节的影响。
| 表 2 各流道入口的多孔跳跃常数 Table 2 Porous-jump constants for different channels. |
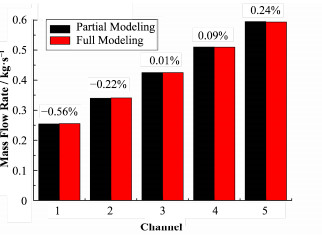
如图 5所示,在腔室内没有流量分配组件的情况下,部分建模迭代求解与完整建模直接求解的结果非常相近,最大绝对误差仅0.56%。
|
图 5 无流量分配组件结果对比 Figure 5 Comparison of flow distribution results without distributor. |
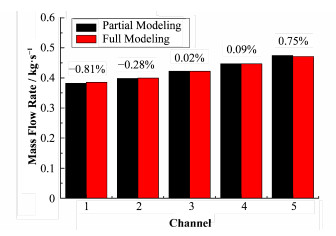
如图 6所示,在入口腔室内存在流量分配组件的工况下,各流道的流量相较于无分配组件的情况有了较大的改变,但是在新的流量分布下,两种算法得到的流量仍非常相近,最大绝对误差仅0.81%。
|
图 6 有流量分配组件结果对比 Figure 6 Comparison of flow distribution results with distributor. |
本文分别利用完整建模直接求解及部分建模迭代求解的方式计算了多层环形燃料板组件在有流量分配组件及无流量分配组件工况下的流量分配情况。经过对比,在两种工况下,两种方法得到的各流道流量最大偏差分别为0.56%及0.81%,证明了部分建模迭代求解方法能够得到与完整建模方法相一致的计算结果。但是,前者对计算资源的需求远小于后者,可以作为将CFD方法应用在板状燃料组件流量分配研究中的优化方案。同时,板状燃料组件属于典型的狭长闭式流道,该方案可以推广到其他狭长闭式流道流量分配的CFD研究中。
| [1] |
李健全, 陈晓明, 李金才. 板状燃料堆芯流道阻塞事故分析[J].
原子能科学技术, 2002, 36 (1) : 76 –79.
LI Jianquan, CHEN Xiaoming, LI Jincai. Analysis on a flow blockage incident at a plate-type fuel reactor[J]. Atomic Energy Science and Technology, 2002, 36 (1) : 76 –79. (  0) 0)
|
| [2] |
宋磊.板状燃料组件堵流事故数值分析[D].哈尔滨:哈尔滨工程大学, 2013
SONG Lei. Numerical analysis of the flow of the plate fuel assembly[D]. Harbin:Harbin Engineering University, 2013 http://cdmd.cnki.com.cn/article/cdmd-10217-1014132135.htm (  0) 0)
|
| [3] |
宋磊, 郭赟, 曾和义. 板状燃料组件入口堵流事故下流场和温度场的瞬态数值计算[J].
核动力工程, 2014, 35 (3) : 6 –10.
SONG Lei, GUO Yun, ZENG Heyi. Numerical analysis on transient flow and temperature field during inlet flow blockage accidents of plate-type fuel assembly[J]. Nuclear Power Engineering, 2014, 35 (3) : 6 –10. (  0) 0)
|
| [4] |
Fan W, Peng C, Guo Y. CFD study on inlet flow blockage accidents in rectangular fuel assembly[J].
Nuclear Engineering and Design, 2015, 292 : 177 –186.
DOI: 10.1016/j.nucengdes.2015.06.016 ( 0) 0)
|
| [5] |
Lu Q, Qiu S, Su H G. Development of a thermal-hydraulic analysis code for research reactors with plate fuels[J].
Annals of Nuclear Energy, 2009, 36 (4) : 433 –447.
DOI: 10.1016/j.anucene.2008.11.038 ( 0) 0)
|
| [6] |
Lu Q, Qiu S, Su G H. Flow blockage analysis of a channel in a typical material test reactor core[J].
Nuclear Engineering and Design, 2009, 239 (1) : 45 –50.
DOI: 10.1016/j.nucengdes.2008.06.016 ( 0) 0)
|
| [7] |
陈道龙, 姜琲. 高通量工程试验堆堆芯燃料元件温度-流量测量装置[J].
核科学与工程, 1984, 4 (6) : 178 –181.
CHEN Daolong, JIANG Bei. The in-core fuel element temperature-flow measurement facility of HFETR[J]. Chinese Journal of Nuclear Science and Engineering, 1984, 4 (6) : 178 –181. (  0) 0)
|
| [8] |
陈道龙, 姜琲. 高通量工程试验堆堆芯燃料元件温度和流量测量[J].
中国核科技报告, 1988 (S2) : 1 –28.
CHEN Daolong, JIANG Bei. The in-core fuel element temperature and flow measurement facility of HFETR[J]. China Nuclear Science and Technology Report, 1988 (S2) : 1 –28. (  0) 0)
|
| [9] |
Fan W, Peng C, Wang G, et al. CFD study on inlet flow blockage accidents in multi-layer annular flow channels[C]. ICONE23(Paper ID:1845), Japan, 2015
( 0) 0)
|
| [10] |
樊文远, 郭赟, 彭常宏. 多层环形流道阻塞事故三维数值分析初步探索[J].
核动力工程, 2016, 37 (1) : 123 –128.
FAN Wenyuan, GUO Yun, PENG Changhong. Preliminary 3D numerical study on flow blockage accident in multi-layer annular flow channels[J]. Nuclear Power Engineering, 2016, 37 (1) : 123 –128. (  0) 0)
|
| [11] |
Fan W, Peng C, Chen Y, et al. A new CFD modeling method for flow blockage accident investigations[J].
Nuclear Engineering and Design, 2016, 303 : 31 –41.
DOI: 10.1016/j.nucengdes.2016.04.006 ( 0) 0)
|
| [12] |
汪利民, 宗桂芳, 尹涛. 600MW反应堆堆芯入口流量分配实验研究[J].
工程热物理学报, 1999, 20 (2) : 185 –189.
WANG Limin, ZONG Guifang, YIN Tao. Test of flow distribution at the core in let of 600 MW reactor[J]. Journal of Engineering Thermophysics, 1999, 20 (2) : 185 –189. (  0) 0)
|
| [13] |
ANASYS. ANASYS FLUENT 12.0 theory guide[Z]. Canonsburg, PA, USA, 2009
( 0) 0)
|


