2. 中国科学院大学 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
熔盐堆是一种采用熔盐作为冷却剂或燃料载体的先进反应堆。与其它先进反应堆一样,熔盐堆在设计上采用了非能动的安全系统,且大多利用了熔盐的自然循环特性[1, 2, 3, 4, 5, 6]。理想状况下,熔盐在热端吸收热量,在冷端释放热量,在平衡状态下,自然循环热端和冷端的热量传递相等。然而在现实中,高温熔盐不可避免地通过管道和回路部件向外界传递热量。这一部分的热量传递通常难以准确计算,可以视为一种热损失。自然循环回路由于熔盐流速较慢,受热损失的影响较强迫循环回路更为明显。热损失对于自然循环的建立和保持均具有重要的影响,特定情况下甚至可能阻碍自然循环的建立或造成熔盐回路的冻堵。因此研究自然循环回路的热损失对于自然循环回路的设计和实验具有重要意义。
中国科学院上海应用物理研究所为研究熔盐的自然循环特性设计建造了熔盐自然循环实验回路[7, 8, 9],如图 1所示。实验回路的管道、容器等部件的外表面均采用包覆式隔热层用于限制回路的热损失。这种形式的保温设计结构相对简单、便于工业应用,但其保温效果的量化分析极少见于报道。鉴于熔盐回路热损失对于自然循环的重要影响,研究掌握熔盐在包覆式隔热层作用下的热量损失规律是极有必要的。

|
图 1 熔盐自然循环实验回路 Figure 1 Molten salt natural circulation experimental loop. |
熔盐储罐在实验回路中用于储存高温熔盐并对其进行保温。其外表面包覆隔热层,连接有各类管道、加热器、探测装置等实验回路常用部件,且外表面和内部不同位置装备有多个温度测量装置,是进行熔盐回路热损失实验研究的理想部件。本课题组因此选取熔盐储罐作为代表部件,对高温熔盐在其中的热量损失情况进行了实验研究,并与数值计算的结果做了比对,总结了在特定隔热设计下熔盐回路热量损失的规律。
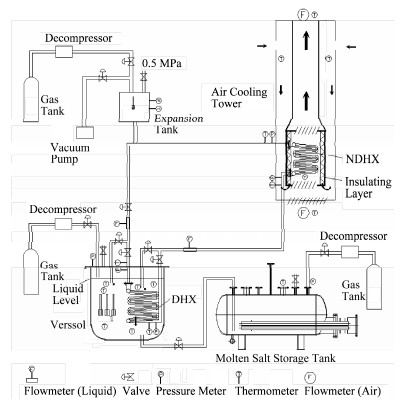
1 实验研究 1.1 实验回路回路主要由熔盐储罐、熔盐池、空冷塔、膨胀罐、管道及伴热系统、气路系统等组成,如图 2所示。回路自然循环设计散热功率为20 kW,最大设计电加热功率为50 kW。
|
图 2 回路示意图 Figure 2 Schematic layout of the loop. |
先进熔盐堆冷却剂及安全系统运行工质多采用氟盐[1, 2, 3, 4],而在各自的稳定液态温度范围内,HTS硝酸盐(53%KNO3-40%NaNO2-7%NaNO3)的主要无量纲准则数变化规律与氟盐具有相似性[10],故熔盐自然循环回路采用HTS硝酸盐。该熔盐熔点低,为415K,比热容高,如式1所示[11],毒性及腐蚀性低、价格便宜,是一种理想的热载体。
| ${{c}_{\operatorname{p}}}=5\ 806-10.833T+7.241\ 3\times {{10}^{-3}}{{T}^{2}}$ | (1) |
式中:cp为相应温度下熔盐的比热容。
熔盐储罐如图 3所示。储罐罐体采用316不锈钢。筒体中部为圆筒,内直径1400mm,两侧为DN1200椭圆封头。罐体厚度12 mm,外部加装厚度150 mm的硅酸铝纤维隔热层,最外层包覆316不锈钢外壳。储罐加热采用工业界广泛采用的插入式加热器,为6根内插套管式电加热器,其结构为内置Cr20Ni80电阻丝,外部为316不锈钢套管,二者之间填充氧化镁绝缘材料,总加热功率为50 kW。实验过程中,储罐内装载6.1t HTS熔盐。

|
图 3 熔盐储罐 Figure 3 Molten salt storage tank. |
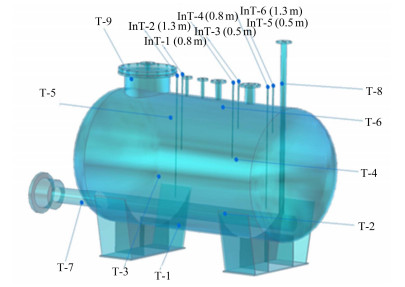
熔盐储罐不同位置布置了9组外贴式热电偶及6组内插式热电偶[12],均为镍铬-镍硅铠装K型热电偶。其中,T-1、T-2、T-3、T-4、T-5、T-6、T-7、T-8、T-9布置于罐体表面,InT-1、InT-2、InT-3、InT-4、InT-5、InT-6置于罐体内部。下文用1、2、3、4、5、6分别代指6组内插式热电偶,如图 4所示(括号内数字表示插入深度)。
|
图 4 储罐热电偶布置图 Figure 4 Layout of the thermo couples installed on or in the tank. |
储罐外表面温度测量选用Testo 720型单通道测温仪,精度等级为±0.5 K[13]。
1.2 实验操作回路使用电加热器持续加热熔盐,直至达到预设温度,并且各内插式热电偶测量温度达到基本一致,即Tmax−Tmin < 5K,然后关闭电加热器,使储罐自然冷却,测量熔盐在自然冷却时的温度变化数据。同时监测9组外贴式热电偶的读数,在其均值为510K、490 K、470 K、450 K、430 K时使用测温仪测量各贴壁热电偶对应外表面位置的温度。
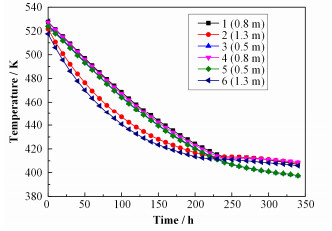
1.3 实验结果储罐自然冷却的降温曲线如图 5所示。从图 5中可以看出,约经过220h,熔盐温度由530K降至凝固点415 K,在凝固点处曲线发生畸变,体现为在熔盐温度下降到415 K左右时,测温点1、2、4、6处熔盐温度下降有一个平缓的阶段,这是因为熔盐凝固释放相变潜热,使得在一定时间内熔盐温度基本保持不变。而3和5未出现这种现象是因为熔盐的凝固是从壁面逐步向内的,而罐内熔盐并未充满,上部空间内为空气,3和5位于熔盐内接近熔盐-空气交界面的位置,其热量主要通过空气由上部隔热层导出。
|
图 5 自然冷却时储罐内各点温度变化 Figure 5 Temperature changes in the tank during natural cooling. |
温度分布方面,6个内插测温点可分为三类:位置最靠近储罐中心的1和4温度始终保持最高,3和5次之,位置最靠近加热器的2和6最低。相同插入深度下,1比4、2比6更靠近储罐中心,故均为前者温度更高。降温速率方面,1、3、4、5趋势基本一致,2、6则与其他4个点体现了显著的不同。
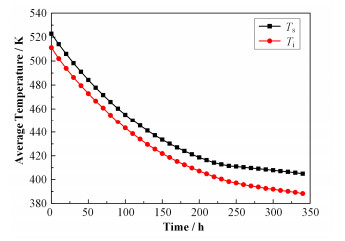
取6个内插测温点平均值Ts为熔盐温度测量值,9个贴壁测温点平均值Ti为储罐隔热层内表面温度测量值,两个变量随时间的变化如图 6所示。
|
图 6 自然冷却时熔盐与储罐隔热层内平均温度对比 Figure 6 Comparison of the average temperatures of the salt and the inner surface during natural cooling. |
课题组通过测量储罐外表面温度和加热器外露段表面温度,发现加热器在断电后仍长时间处于较高温状态,如表 1所示。由此推测,2及6与其它测温点降温规律不同是由于2及6靠近底部加热器。内插式加热器由于工作需要,一段浸没在熔盐中,另外一段则暴露在外部空气中。这样,断电状态的加热器本身成为了一个散热通道,将罐内熔盐的热量源源不断地导出至外界空气中。
| 表 1 储罐不同时刻的平均温度 Table 1 Average temperatures of the tank at different times. |
熔盐在自然冷却过程中的总热损失可由式(2)计算:
| $ \Phi=\frac{\text{1}}{\Delta t}\int_{{{T}_{\text{1}}}}^{{{T}_{\text{2}}}}{{{c}_{\operatorname{p}}}m\text{d}T} $ | (2) |
此处将式(1)代入;m为储罐内熔盐的总质量;T1和T2分别为△t时间段熔盐始、末温度。
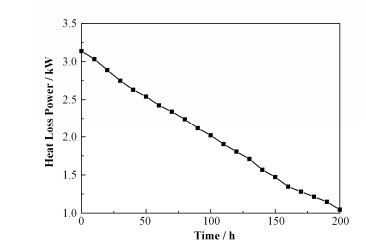
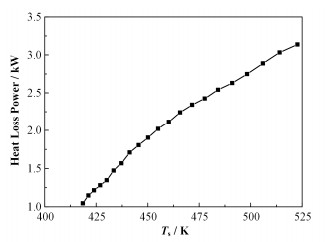
计算得到各时间段熔盐储罐内熔盐的总热损失,拟合得到熔盐储罐的总热损失随时间及熔盐温度变化的曲线,如图 7、8所示,同时拟合得到热损失与时间及熔盐温度关系式如式(3)、(4)所示:
|
图 7 储罐热损失随时间的变化曲线 Figure 7 Heat loss of the tank and the salt vs. time. x |
|
图 8 储罐热损失随温度的变化曲线 Figure 8 Heat loss of the tank and the salt vs. temperature. |
| $\Phi=3.08-\text{0}\text{.01}t$ | (3) |
| $ \Phi=-25.84+0.1{{T}_{\operatorname{s}}}-8.56\times {{10}^{-5}}T_{\operatorname{s}}^{2} $ | (4) |
式中:Φ为热损失,kW;t为时间,h;Ts为熔盐平均温度,K。
2 数值计算 2.1 计算公式在任意时刻,熔盐储罐的总热损失,由以下几部分组成:
| $ \Phi={{\Phi }_{1}}+{{\Phi }_{2}}+{{\Phi }_{3}}\text{+}{{\Phi }_{\text{4}}} $ | (5) |
式中:Φ为储罐内熔盐总的热损失;Φ1为通过罐体及隔热层的导热及对流热损失;Φ2为通过内插式加热器的导热及对流热损失;Φ3为储罐外表面的辐射热损失;Φ4为加热器与空气接触面的辐射热损失。
本文采用商用计算传热学程序ANSYS CFX[14]计算熔盐储罐导热和对流换热部分的热损失Φ1和Φ2。
辐射热损失Φ3由式(6)计算:
| ${{\Phi }_{3}}=A{{\varphi }_{12}}{{C}_{0}}\varepsilon [{{(\frac{{{T}_{\operatorname{w}}}}{100})}^{4}}-{{(\frac{{{T}_{\infty }}}{100})}^{4}}]$ | (6) |
式中:A为储罐外表面积;φ12为平均角系数,因储罐完全被空气包围,取1;C0为黑体辐射常量,取5.67 W·m-2·K-4;ε为316不锈钢发射率;Tw为实验测得的储罐外表面温度,K;T∞为空气温度,取295K。Φ4计算方法同理。
2.2 数值模型实验过程中,除底部外,储罐内各位置的熔盐温度及壁面温度相差很小,故储罐热损失计算基于如下假设:(1)忽略各开口及相应密封法兰等不规则结构;(2)忽略熔盐与储罐内表面的自然对流,假设熔盐与储罐内壁只存在导热;(3)假设各时刻储罐内表面温度处处相等。
对于一般的流动或传热问题,通用形式的控制方程如下:
| $ \frac{{\partial (\rho \phi )}}{{\partial t}} + \nabla \cdot (\rho {\rm{\vec u}}\phi ) = \nabla \cdot (\Gamma {\kern 1pt} \nabla \phi ) + S $ | (7) |
式中:ρ表示密度;ϕ为通用变量,可以是速度、温度等;S为广义源项,它代表控制方程中除去非稳态项、对流项及扩散项之外的所有其他项之和;Г为对应于变量ϕ的广义扩散系数,对于传热问题:
| $\Gamma=\lambda \text{/}{{c}_{\operatorname{p}}}$ | (8) |
式中:λ为热导率。
隔热层为固体,故略去对流项及源项,将式(8)代入式(7),得到隔热层的导热微分方程:
| $ \rho {{c}_{\operatorname{p}}}\frac{\partial T}{\partial t}=\lambda {{\nabla }^{2}}T $ | (9) |
规定与外界空气接触的隔热层壁面为第三类边界条件:
| $-\lambda {{(\frac{\partial T}{\partial n})}_{\operatorname{w}}}=h({{T}_{\operatorname{w}}}-{{T}_{\infty }}) $ | (10) |
式中:n为隔热层表面的外法线方向;h为隔热层外表面空气自然对流换热系数。
本文几何建模采用SolidWorks 2014,网格划分采用ICEM CFD 14.5,计算求解采用CFX 14.5,后处理采用CFD−Post 14.5。
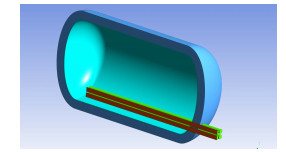
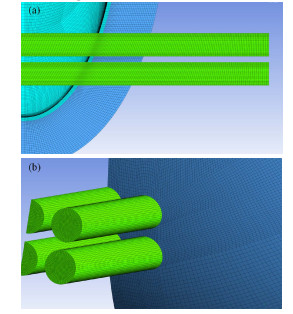
基于储罐的对称性,建立1/2储罐模型,如图 9所示。划分的全六面体网格,如图 10所示。沿法向,罐体网格层数为6,隔热层网格层数为30,罐体、隔热层、加热器之间所有Interface网格节点均一一对应,并对Interface两端网格尺寸做了调整以实现网格尺寸的平滑过渡。网格总数约480万,网格质量均大于0.35,网格质量超过0.8的网格占网格总数的95%以上,满足计算要求。
|
图 9 储罐三维模型 Figure 9 3D model of the tank. |
|
图 10 储罐网格划分(a)对称面,(b)前端 Figure 10 Meshing of the tank. (a) Symmetry, (b) Front view |
CFX中各固体区域传热模型均选用Thermal Energy(热焓模型),离散格式选用High resolution,收敛精度取10−6。物性选用如下:罐体热导率取18 W·(m·K)−1,隔热层热导率取0.08 W·(m·K)−1,将加热器三种材料热物性按照其在加热器横截面积所占比例进行平均,计算得到一个等效热导率32.41 W·(m·K)−1用于计算。
隔热层及加热器外表面均施加对流换热边界条件,由于储罐安装于室内,而大空间无风状态下空气的自然对流换热系数范围约为1-10W·m−2·K−1[15],考虑本文实验周期较长,故隔热层外部换热系数取平均值5 W·m−2·K−1。环境温度取295 K。储罐内壁分别设置510 K、490 K、470 K、450 K、430 K进行计算求解,读取储罐罐体内表面的热通量Φ0.1及加热器与熔盐接触面的热通量Φ0.2,得到:
| ${{\Phi }_{1}}=2{{\Phi }_{0, 1}}$ | (11) |
| ${{\Phi }_{2}}=2{{\Phi }_{0, 2}}$ | (12) |
利用所建立的数值模型,对应不同内表面温度下储罐整体的温度分布如图 11所示。在储罐内部高温熔盐和储罐外部空气自然对流的双重作用下,加热器沿自身轴向形成了多个温度分层。
计算得到不同温度下的热损失功率如表 2所示。计算值与实验值间的对比如图 12所示,相对误差均小于10%,其中加热器热损失量占总量的14%-16%。隔热层单位面积热损失随隔热层内表面温度的变化规律如图 13所示。
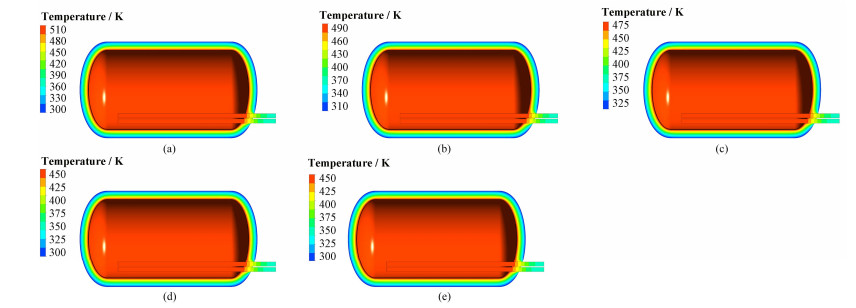
|
图 11 不同内表面温度下储罐的温度场(a) 510K,(b) 490K,(c) 470K,(d) 450K,(e) 430K Figure 11 Temperature fields at different inner surface temperatures. (a) 510K, (b) 490K, (c) 470K, (d) 450K, (e) 430K |
| 表 2 熔盐储罐热损失功率 Table 2 Power of the heat loss of the salt tank. |
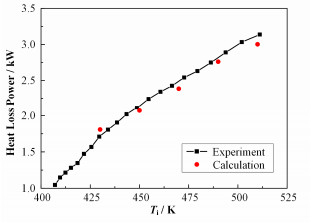
|
图 12 热损失功率计算值与实验值的对比 Figure 12 Comparison of calculated and experimental heat loss power. |
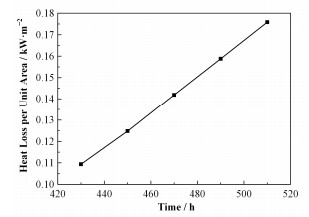
|
图 13 单位面积热损失随温度的变化曲线 Figure 13 Heat loss power per unit area vs. temperature. |
选取熔盐储罐作为代表,对熔盐自然循环实验回路采用的包覆式隔热设计的性能进行了实验研究与数值计算,获得了隔热层热损失功率的定量结果,可用于熔盐池及管道的热损失功率预测。
当熔盐温度处于415-523 K时,熔盐储罐总热损失功率在1-3.14kW之间。隔热层内表面温度分别为510 K、490 K、470 K、450 K、430 K时,隔热层单位面积热损失分别为0.176 kW、0.159 kW、0.142kW、0.125 kW、0.109 kW。在不同温度下,熔盐储罐热损失计算值与实验值的误差均在10%以内,说明计算模型较好地模拟了现实的热损失情况,且除加热器外,与储罐相连的各种部件造成的热损失较少。包覆式隔热层用于自然循环回路效果较好,回路热量损失在可控范围内。
位于熔盐储罐下部的加热器造成的热损失占储罐热损失总量的15%左右,使得底部熔盐温度明显低于上部熔盐的温度。采用插入式加热器时需要注意加热器在停止加热后造成的热量损失。
| [1] |
Forsberg C W, Peterson P F, Pickard P S. Molten-salt-cooled advanced high-temperature reactor for production of hydrogen and electricity[J].
Nuclear Technology, 2003, 144 (3) : 289 –302.
( 0) 0)
|
| [2] |
Ingersoll D T, Clarno K T, Forsberg C W, et al. Status of physics and safety analyses for the liquid-salt-cooled very high-temperature reactor (LS-VHTR)[R]. ORNL/TM-2005/218, Oak Ridge, Tennessee:Oak Ridge National Laboratory, 2005
http://web.ornl.gov/~webworks/cppr/y2001/pres/124384.pdf ( 0) 0)
|
| [3] |
Holcomb D E, Peretz F J, Qualls A L. Advanced high temperature reactor systems and economic analysis[R]. ORNL/TM-2011/364, Oak Ridge, Tennessee:Oak Ridge National Laboratory, 2011
http://www.zoominfo.com/p/A.-Qualls/1547359682 ( 0) 0)
|
| [4] |
Forsberg C W, Hu L W, Peterson P F, et al. Fluoride-salt-cooled high-temperature reactors (FHRs) for power and process heat[R]. MIT-ANP-TR-157, Cambridge, MA:Massachusetts Institute of Technology, 2014
http://web.mit.edu/nse/pdf/researchstaff/forsberg/FHR%20Project%20Report%20ANP-TR-157%20MIT-UCB-UW.pdf ( 0) 0)
|
| [5] |
Rouch H, Geoffroy O, Rubiolo P, et al. Preliminary thermal-hydraulic core design of the molten salt fast reactor (MSFR)[J].
Annals of Nuclear Energy, 2014, 64 (2) : 449 –456.
DOI: 10.1016/j.anucene.2013.09.012 ( 0) 0)
|
| [6] |
Serp J, Allibert M, Beneš O, et al. The molten salt reactor (MSR) in generation IV:overview and perspectives[J].
Progress in Nuclear Energy, 2014, 77 (11) : 308 –319.
DOI: 10.1016/j.pnucene.2014.02.014 ( 0) 0)
|
| [7] |
Cai C X, He Z Z, Chen K. Design and construction of a high-temperature molten salt natural circulation test loop[C]. 2016 International Congress on Advances in Nuclear Power Plants, San Francisco, CA, 2016
( 0) 0)
|
| [8] |
林超, 蔡创雄, 王凯, 等. 硝酸盐自然循环回路空冷塔性能分析[J].
核技术, 2014, 37 (12) : 120601 .
DOI: 10.11889/j.0253-3219.2014.hjs.37.120601 LIN Chao, CAI Chuangxiong, WANG Kai, et al. Performance analysis of the air cooling tower for nitrate natural circulation loop[J]. Nuclear Techniques, 2014, 37 (12) : 120601 . DOI: 10.11889/j.0253-3219.2014.hjs.37.120601 (  0) 0)
|
| [9] |
王凯, 蔡创雄, 何兆忠, 等. 硝酸盐自然循环回路系统特性分析[J].
核技术, 2015, 38 (4) : 040602 .
DOI: 10.11889/j.0253-3219.2015.hjs.38.040602 WANG Kai, CAI Chuangxiong, HE Zhaozhong, et al. Characteristics analysis of nitrate natural circulation loop[J]. Nuclear Techniques, 2015, 38 (4) : 040602 . DOI: 10.11889/j.0253-3219.2015.hjs.38.040602 (  0) 0)
|
| [10] |
刘晓晶, 李冬, 鲍晗.硝酸盐自然循环实验回路模化分析报告[R].上海:中国科学院上海应用物理研究所, 2014
LIU Xiaojing, LI Dong, BAO Han. The nitrate natural circulation loop modeling analysis report[R]. Shanghai:Shanghai Institute of Applied Physics, Chinese Academy of Sciences, 2014 (  0) 0)
|
| [11] |
Janz G J, Tomkins R P T. Physical properties data compilations relevant to energy storage IV molten salts:data on additional single and multi-component salt systems[R]. Troy, NY:Molten Salts Data Center Cogswell Laboratory Rensselaer Polytechnic Institute, 1981:786-795
( 0) 0)
|
| [12] |
孔祥波, 蔡创雄, 傅远.硝酸盐自然循环实验回路工程设计报告[R]. TMSR-SE-NS-TR-2013-35, 上海:中国科学院上海应用物理研究所, 2013
KONG Xiangbo, CAI Chuangxiong, FU Yuan. The nitrate natural circulation loop engineering design report[R]. TMSR-SE-NS-TR-2013-35, Shanghai:Shanghai Institute of Applied Physics, Chinese Academy of Sciences, 2013 (  0) 0)
|
| [13] |
Testo 720使用说明书[Z].德图仪器, 2015
Instruction manual Testo 720[Z]. Testo AG, 2015 (  0) 0)
|
| [14] |
陶文铨.
数值传热学. :[M]. 西安: 西安交通大学出版社, 2001 .
TAO Wenquan. Numerical heat transfer[M]. Xi'an: Xi'an Jiaotong University Press, 2001 . (  0) 0)
|
| [15] |
陈孟, 黄庆, 翁羽, 等.自然对流换热系数计算方法研究[C].第十七届全国反应堆结构力学会议, 上海, 2012
CHEN Meng, HUANG Qing, WENG Yu, et al. The computational method for heat transfer film coefficient of nature convection[C]. 17th National Conference on Structural Mechanics in Reactor Technology, Shanghai, 2012 (  0) 0)
|


