2. 中国科学院大学 北京 100049;
3. 重庆理工大学 重庆 400050
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Chongqing University of Technology, Chongqing 400050, China
随着同步辐射技术的应用研究不断深入,科研工作者对同步辐射光束线的性能要求越来越高,在某些领域光束线聚焦后的光斑尺寸需求由微米量级提高到纳米量级[1-2],这对同步辐射用光学反射镜的表面质量提出了很高的要求。镜面面形误差的均方根(Root Mean Square, RMS)是评价镜面质量的一个重要指标,美国布鲁克海文国家实验室提出用于第三代同步辐射光源的光学反射镜的面形误差RMS值应优于50nm[3-4],这使得精确地检测反射镜面形并合理地评价其表面质量显得尤为重要。
目前用于同步辐射光学反射镜表面检测的主要设备是长程面形仪(Long Trace Profiler, LTP),它是一种斜率测量设备,通过一维顺序扫描获得扫描线上采样点的斜率分布,然后将斜率分布积分得到镜面面形。自1987年Takacs[5-6]基于光笔干涉仪发明了LTP后,世界各地的同步辐射光源纷纷建立了LTP装置,经过20多年的广泛应用与发展,出现了LTP-Ⅰ、LTP-Ⅱ、LTP-Ⅲ、DLTP、PP-LTP、NOM(Nanometer Optical Component Measuring Machine)等多种改进装置[7-11],其中NOM用自准直仪代替了LTP中复杂的测量光路,是目前用于同步辐射光学反射镜表面斜率测量精度最高的仪器,其精度可达50nrad,甚至更好。
使用LTP精确测量镜面面形后,需在采样点处将镜面的理想面形从测量数据中扣除,计算出镜面的面形误差,而同步辐射用光学反射镜一般为窄长型,长度可达2m,子午面曲率半径通常从数百米到数十千米,由于镜面曲率半径过大,无法直接测量,因此需要采用曲线拟合算法拟合出最佳的镜面几何参数。目前,主要采用最小二乘法拟合镜面几何参数[12],由于同步辐射用光学反射镜的曲率半径较大,而其长度相对于其曲率半径过小,使得测量数据只集中在理想面形上很小的一段区域,这给精确拟合镜面的几何参数带来了很大困难,进而影响镜面面形误差RMS值的可靠性。为了实现对长程面形仪器测量数据这种小样本数据进行精确拟合,同时更加合理地评价高精度的同步辐射用光学反射镜的表面质量,本文通过数值模拟引入可能影响拟合算法精度的因素,对基于代数距离的最小二乘法、基于几何距离的最小二乘法及遗传算法进行对比,寻找最适合长程面形仪测量数据的曲线拟合算法。
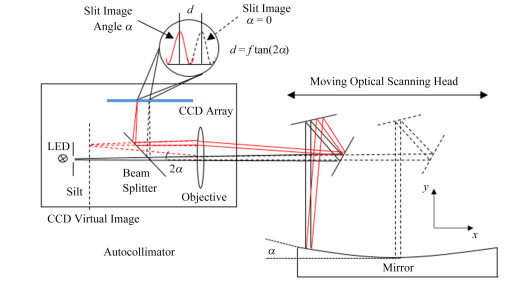
1 斜率测量原理上海同步辐射光源目前使用NOM进行反射镜的面形检测,其主要由自准直仪和光学扫描头组成,自准直仪用于测量并记录待测镜面反射光线的偏转角度,光学扫描头主要由双反射镜组成,双反射镜构成类五棱镜结构用于对光线进行90°偏转。如图 1所示,自准直仪中的发光二极管(Light Emitting Diode, LED)光源发出的光束经过狭缝和准直透镜产生一束窄距平行光,经过双反射镜后垂直入射到待测镜面,待测镜面的反射光束再次经双反射镜偏转后返回自准直仪,光束经过透镜和分束器聚焦到电荷耦合元件(Charge-coupled Device, CCD)上,通过CCD上狭缝像的位置变化可得到采样点处的斜率tanα。
|
图 1 纳米光学部件测量仪检测原理 Figure 1 Measuring principle of Nanometer Optical Component Measuring Machine (NOM). |
采样点处的斜率S(x)由式(1)给出,其中:y为镜面面形;x轴方向为扫描方向;α为镜面面形在采样点处的切线与x轴的夹角。
| $S(x)=\tan \alpha={\mathop{\rm d}\nolimits} y/{\mathop{\rm d}\nolimits} x$ | (1) |
扫描头沿x轴方向移动扫描,扫描间隔为△x,依次得到m个采样点处的斜率数据S(xm),对斜率数据进行空间积分后可得到镜面的面形h(xk),如式(2):
| $h({x_k})=h({x_0})+\sum\limits_{m=1}^k {\frac{{\Delta x}}{2}} [S({x_m})+S({x_{m-1}})]$ | (2) |
式中:h(x0)为第一个采样点处的高度。
采用曲线拟合算法对h(xk)拟合得到镜面的最佳拟合面形I(xk),采样点xk处镜面的面形误差由式(3)给出:
| $R({x_k})=h({x_k})-I({x_k})$ | (3) |
镜面面形误差R(xk)的RMS由式(4)给出:
| ${\mathop{\rm RMS}\nolimits}=\sqrt {\frac{1}{k}\sum\limits_{i=1}^k {{R^2}({x_i})} } $ | (4) |
本文主要采用最小二乘法和遗传算法,最小二乘法根据目标函数不同分为基于代数距离的最小二乘法和基于几何距离的最小二乘法,以下简称为代数法和几何法。
2.1 基于代数距离的最小二乘法基于代数距离的最小二乘法(Algebraic distance least square method, ALS)使用隐式方程
基于几何距离的最小二乘法(Geometric distance least square method, GLS)将误差距离d定义为给定数据点到拟合曲线的最短距离,对于每一个给定数据点,在拟合曲线上有一个对应的最短距离点,找到最短距离点,即可求出最短距离[14]。对于圆锥曲线来说,目标函数
| $h=I(a)+e$ | (5) |
式中:I代表非线性连续可微的关于a的观测函数;e代表误差。待优化的目标函数为:
| ${{\sigma }^{2}}={{[h-I(a)]}^{T}}[h-I(a)]$ | (6) |
迭代过程:
| $ {{\left.\frac{\partial I}{\partial a} \right|}_{{{a}_{k}}}}\Delta a=h-I({{a}_{k}}) $ | (7) |
| ${{a}_{k+1}}={{a}_{k}}\text{+}\lambda \Delta a$ | (8) |
选择代数法的拟合结果作为初始向量a0,迭代步长系数λ=1.3,迭代终止条件:
| $\sigma _{k+1}^{2}-\sigma _{k}^{2}\approx 0 \text{or} \Delta a\approx 0$ | (9) |
式(7)中出现的矩阵求偏导为雅克比矩阵J:
| ${{J}_{ij}}=\frac{\partial {{I}_{i}}}{\partial {{a}_{j}}}$ | (10) |
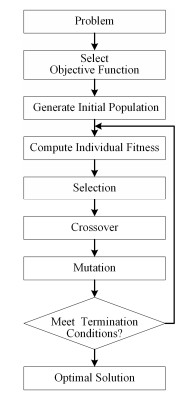
遗传算法(Genetic algorithm, GA)是一种随机搜索算法,模拟自然选择和遗传操作,算法流程如图 2所示[15],遗传算法只需设计好待优化的目标函数和参数搜索空间,通过选择,交叉和变异操作使种群中个体不断进化,最终收敛到最优解。本文采用实数编码方式,选择算子采用锦标赛选择算法,交叉算子采用中间重组,变异算子采用Muhlenbein变异,以模拟镜面的面形误差的RMS值做为待优化目标函数。
|
图 2 遗传算法流程图 Figure 2 Flow chart of genetic algorithm. |
在实际应用中,面形误差对子午线方向的聚焦影响很大,因此本文以镜面面形误差的RMS值作为算法拟合精度的评定标准。模拟部分只研究平面镜和大曲率半径柱面镜的面形拟合,平面镜因重力作用弯曲,会产生一个很大的曲率半径,可近似为柱面镜。NOM沿柱面镜准线扫描后,积分生成的面形是一段圆弧。因此,根据NOM等间隔采样的特点,等弦长间隔生成一段半径为R的标准圆弧模拟镜面理想面形,在理想面形中加入高斯白噪声模拟镜面测量面形(当高斯白噪声的均值μ为0时,根据高斯分布特点,噪声的振幅可近似为3σ)。
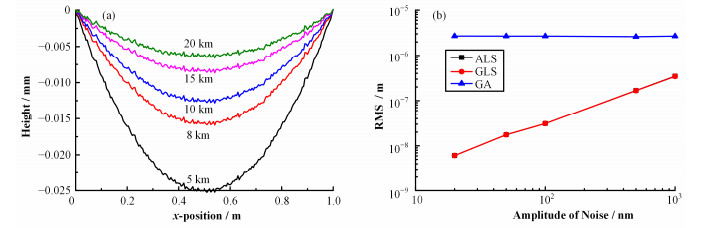
3.1 镜面曲率半径对于NOM这种小样本测量数据,面形的曲率半径越大,测量数据所包含的理想曲面信息越少,不同的拟合算法精度会出现差异。为了研究曲线拟合算法对大曲率半径面形拟合的适用性,生成弦长为1m、数据点x轴间隔为5mm、噪声振幅为100nm、半径为R的5组模拟面形,如图 3(a)所示。采用代数法、几何法及遗传算法对5组模拟面形分别拟合,三种算法拟合精度与镜面曲率半径的关系如图 3(b)所示。
|
图 3 曲率半径不同的模拟面形(a)和曲率半径对算法拟合精度的影响(b) Figure 3 Profiles of different radii (a) and influence of radius on the accuracy of fitting algorithm (b). |
对比三种算法的拟合结果可发现,随着半径增大,代数法和几何法拟合精度基本保持不变,面形误差RMS值在30nm左右,近似等于模拟噪声的均方差(33.3nm),这表明在采样范围较小的情况下,二者依然能够有效地拟合镜面的理想面形。而遗传算法拟合精度随半径增大单调递增,在镜面曲率半径为20km时,拟合精度最高,面形误差RMS为2.7mm,远大于面形误差的均方差,遗传算法出现早熟现象,在一个局部最优值处收敛,这可能是由于曲率半径较大,造成搜索空间过大,算法无法有效地收敛到最优解。
3.2 测量环境噪声若曲线拟合算法对噪声敏感,则微小的测量环境噪声(诸如振动、空气流动和温度变化等)也会导致镜面几何参数的拟合结果不精确,进而影响到面形误差RMS值的可靠性。
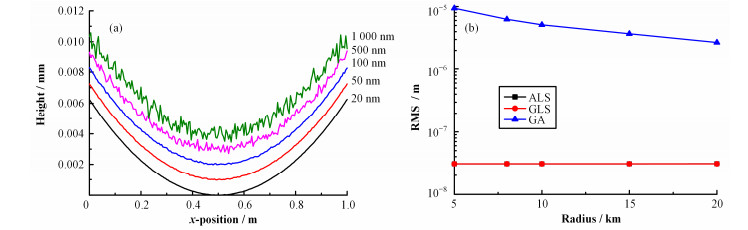
为研究测量环境噪声大小对曲线拟合算法拟合精度的影响,如图 4(a)所示,生成弦长为1m、数据点x轴间隔为5mm、半径R=20km、噪声振幅为A的5组模拟面形。三种算法拟合精度与噪声振幅的关系如图 4(b)所示,代数法和几何法拟合精度随噪声振幅增大单调递减,面形误差的RMS值近似等于噪声的均方差,而遗传算法的拟合精度不随噪声振幅增大而发生变化,面形误差的RMS值为2.7mm。这表明代数法和几何法对噪声的鲁棒性好,在存在噪声的情况下依然可以精确拟合镜面几何参数,而遗传算法依然出现早熟,在局部最优解处收敛,无法识别噪声的变化。
|
图 4 噪声不同的模拟面形(a)和噪声对算法拟合精度的影响(b) Figure 4 Profiles of different noise intensities (a) and influence of noise on the accuracy of fitting algorithm (b). |
NOM是通过测量采样点处反射光相对入射光的偏转角度来获得采样点处的斜率,待测镜面放置时存在一个倾斜角度,对于不同的倾斜角度,相同采样点处反射光相对于入射光的偏转角度不同,造成采样点处的测量斜率发生变化,进而得到不同的积分面形。当镜面测量姿态变化时相当于测量同一圆上不同位置的圆弧,如图 5(a)所示。对斜率分布进行积分时,通常将第一个采样点设置为原点,因此将各段圆弧起始点平移到一公共原点。平移后,同一镜面不同测量姿态下的面形如图 5(b)所示。若曲线拟合算法对圆弧偏转和平移敏感,则无法精确拟合测量姿态变化后镜面的几何参数,镜面面形误差的RMS值将发生变化。
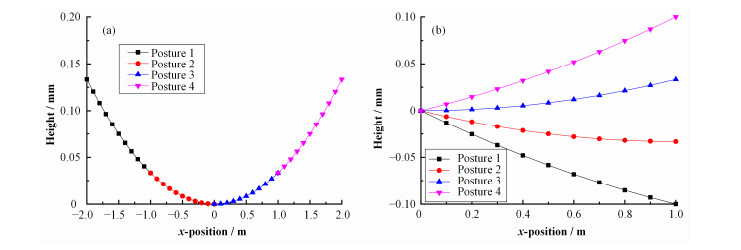
|
图 5 镜面不同测量姿态的面形(a)和平移后的面形(b) Figure 5 Profiles of different postures (a) and profiles after shifting (b). |
镜面不同测量姿态可通过圆弧的偏转和坐标平移来模拟,生成弦长为1m、数据点x轴间隔为5mm、噪声振幅为100nm、半径R=20km的一段模拟面形,将模拟面形沿理想面形曲线(半径为R的整圆)移动,每偏转一定角度即一个不同的测量姿态,将偏转后的模拟面形的第一个点平移到坐标原点,实际测量中,镜面倾斜角度不同引起的面形高度变化不会超过1mm,因此将单次偏转角度设为10-4rad,旋转10次,生成10组模拟数据,如图 6(a)所示,不同姿态的模拟数据高度差距最大为0.8mm。图 6为明确区分各面形,只画出了5组面形。

|
图 6 不同测量姿态的模拟面形(a)和测量姿态对算法拟合精度的影响(b) Figure 6 Profiles of different measurement postures (a) and influence of measured postures on the accuracy of fitting algorithm (b). |
算法拟合精度与镜面测量姿态的关系如图 6(b)所示,当测量姿态发生变化时,几何法和遗传算法拟合精度保持不变,几何法拟合精度较高,面形误差的RMS值保持在30nm左右,遗传算法拟合精度较低,面形误差的RMS值在2.7mm左右。而代数法拟合精度随镜面偏转角度增大单调降低,当偏转角度为0.5mrad时,面形误差的RMS值已经增大到68.8nm。
3.4 小结通过以上对比可发现,几何法和代数法相较于遗传算法更适合大曲率半径的面形拟合,抗噪能力更强,但代数法对镜面测量姿态敏感,当镜面偏转一定角度时,精度严重下降,这可能是由于代数法存在以下缺点:
1) 误差距离定义无物理意义;
2) 拟合误差不可避免地存在权重;
3) 拟合参数对坐标变换不具备不变性。
若镜面测量姿态调节到理想状态,此时代数法和几何法精度接近,而代数法运算速度快,只需0.0001s,则代数法优势更大,几何法由于需要求解与测量点数相关的超定方程,需要进行多次迭代才能得到理想结果,耗费时间较长。但实际测量中,调节镜面测量姿态是一个很费时的工作,姿态调节好后,需等待振动,空气流动和实验室温度稳定后才能开始测量,利用几何法对测量姿态不敏感这一特性,可以节省很多调节时间。同时,反射镜放置在载镜台的位置发生变化时,载镜台表面的面形缺陷也会引起镜面测量姿态发生变化,此时几何法的拟合结果将更可靠。
4 结语通过对模拟面形的拟合结果分析可知:镜面的测量姿态是影响镜面理想面形拟合结果的重要因素,基于几何距离的最小二乘法适用于大曲率半径的面形拟合,对噪声的鲁棒性较好,对镜面测量姿态不敏感。因此,基于几何距离的最小二乘法是更适合长程面形仪柱面镜测量数据的拟合算法。
| [1] |
Alcock S G, Sawhney K J S, Scott S, et al. The Diamond-NOM:a non-contact profiler capable of characterizing optical figure error with sub-nanometre repeatability[J].
Nuclear Instruments and Methods in Physics Research, 2010, A616 (2) : 224 –228.
DOI: 10.1016/j.nima.2009.10.137 ( 0) 0)
|
| [2] |
Mimura H, Handa S, Kimura T, et al. Breaking the 10 nm barrier in hard-X-ray focusing[J].
Nature Physics, 2010, 6 (2) : 122 –125.
DOI: 10.1038/NPHYS1457 ( 0) 0)
|
| [3] |
Takacs P Z, Qian S. Metrology laboratory requirements for third-generation synchrotron radiation sources[C]. Proceedings of the Society of Photo-optical Instrumentation Engineers, San Diego, CA, USA, 1997:160-167. DOI:10.1117/12.295555
10.1117/12.295555 ( 0) 0)
|
| [4] |
Assoufid L, Hignette O, Howells M, et al. Future metrology needs for synchrotron radiation grazing-incidence optics[J].
Nuclear Instruments and Methods in Physics Research, 2001, A467 : 267 –270.
DOI: 10.1016/S0168-9002(01)00296-0 ( 0) 0)
|
| [5] |
Takacs P Z, Qian S, Colbert J. Design of a long trace surface profiler[C]. Proceedings of the Society of Photo-optical Instrumentation Engineers, Los Angeles, CA, USA, 1987:59-64. DOI:10.1117/12.939842
10.1117/12.939842 ( 0) 0)
|
| [6] |
Takacs P Z, Su-chen K F, Church E L, et al. Long trace profile measurements on cylindrical aspheres[C]. Proceedings of the Society of Photo-optical Instrumentation Engineers, Denver, CO, USA, 1999:266-274. DOI:10.1117/12.948082
10.1117/12.948082 ( 0) 0)
|
| [7] |
Qian S, Jark W, Takacs P Z. The penta-prism LTP:a long-trace-profiler with stationary optical head and moving penta prisma[J].
Review of Scientific Instruments, 1995, 66 (3) : 2562 –2569.
DOI: 10.1063/1.1145658 ( 0) 0)
|
| [8] |
Kirschman J L, Domning E E, McKinney W R, et al. Performance of the upgraded LTP-Ⅱat the ALS optical metrology laboratory[C]. Proceedings of the Society of Photo-optical Instrumentation Engineers, San Diego, CA, USA, 2008:70770A-12. DOI:10.1117/12.796335
10.1117/12.796335 ( 0) 0)
|
| [9] |
Senba Y, Kishimoto H, Ohashi H, et al. Upgrade of long trace profiler for characterization of high-precision X-ray mirrors at SPring-8[J].
Nuclear Instruments and Methods in Physics Research, 2010, A616 (2) : 237 –240.
DOI: 10.1016/j.nima.2009.12.007 ( 0) 0)
|
| [10] |
Yashchuk V V, Barber S, Domning E E, et al. Sub-microradian surface slope metrology with the ALS developmental long trace profiler[J].
Nuclear Instruments and Methods in Physics Research, 2010, A616 (2) : 212 –223.
DOI: 10.1016/j.nima.2009.10.175 ( 0) 0)
|
| [11] |
Siewert F, Noll T, Schlegel T, et al. The nanometer optical component measuring machine:a new Sub-nm topography measuring device for X-ray optics at BESSY[C]. AIP Conference Proceedings, San Francisco, CA, USA, 2004, 705(1):847-850. DOI:10.1007/978-3-540-74561-7_11
10.1007/978-3-540-74561-7_11 ( 0) 0)
|
| [12] |
Assoufid L, Rommeveaux A, Ohashi H, et al. Results of X-ray mirror round-robin metrology measurements at the APS, ESRF, and Spring-8 optical metrology laboratories[C]. Proceedings of the Society of Photo-optical Instrumentation Engineers, San Diego, CA, USA, 2005:129-140. DOI:10.1117/12.623209
10.1117/12.623209 ( 0) 0)
|
| [13] |
李培培.曲线造型中关于拟合、参数化及形状优化问题的研究[D].山东:山东大学, 2012
LI Peipei. Research on fitting, parameterization and shape optimization problems of curve modeling[D]. Shandong:Shandong University, 2012 http://cdmd.cnki.com.cn/article/cdmd-10422-1012461424.htm (  0) 0)
|
| [14] |
Ahn S J, Rauh W, Warnecke H J. Least-squares orthogonal distances fitting of circle, sphere, ellipse, hyperbola, and parabola[J].
Pattern Recognition, 2001, 34 (12) : 2283 –2303.
DOI: 10.1016/S0031-3203(00)00152-7 ( 0) 0)
|
| [15] |
雷英杰, 张善文, 李续武.
MATLAB遗传算法工具箱及其应用[M]. 西安: 西安电子科技大学出版社, 2005 .
LEI Yingjie, ZHANG Shanwen, LI Xuwu. MATLAB genetic algorithm toolbox and its application[M]. Xi'an: Xidian University Press, 2005 . (  0) 0)
|


