第四代同步辐射光源仍处于研究阶段,但得到大家公认的是能量回收加速器和自由电子激光都是潜力非常大的第四代光源。ERL-FEL (Energy recovery linac- Free electron laser)装置[1]通过同一台直线加速器将能量回收加速器和自由电子激光结合到一起。电子在各区段输运时,电子的空间电荷效应会增大束流的发散度,偏离束流中心而形成束晕粒子,束晕粒子在振幅很大时,很容易丢失在器壁上,引起束流损失;在脉冲运行模式下,瞬态束流负载效应也会引起粒子丢失;束流准直误差也会引起束流损失。束流损失不仅限制了束流的提高,而且带来了辐射屏蔽等方面的一系列问题。高能电子加速器正常运行时,损失的电子(E>10 MeV)与加速器结构材料(如真空管、支撑结构)相互作用,产生的光子与加速器材料发生光核反应产生中子[2],在屏蔽层外形成泄漏剂量率,对工作人员甚至公众带来直接的放射性危害。严格控制粒子损失率是降低辐射屏蔽设计难度、减小加速器隧道感生放射性的有效途径。
本文利用离散抽样的方法实现ERL装置多个损失源项的整合,在同一FLUKA用户程序中实现多源抽样,并和多个源项分开处理的累积结果进行对比,结果表明两者符合较好;然后修改多源抽样用户程序的参数,扩展到FEL装置屏蔽设计中。
1 设计方法在屏蔽设计中,国际上普遍采用半经验的分析方法和蒙特卡罗方法。半经验方法很大程度上依赖于设计者的主观经验[2],可对蒙特卡罗计算进行简单验证。随着计算机技术的进步和蒙特卡罗算法的改进,蒙特卡罗程序可以解决复杂几何结构的屏蔽问题,并得到高精度的计算结果。
1.1 简介FLUKA[2]是由意大利国立核物理研究所开发的一个计算粒子输运和粒子与物质相互作用的通用计算工具,可以模拟几十种不同的粒子,处理非常复杂的几何结构。Flair和SimpleGeo是FLUKA的辅助软件,可以方便编写一定格式的FLUKA用户程序,查看几何结构和剂量分布。
本文在使用FLUKA建立几何模型时,引入方差减小技巧,将主体墙由内向外划分许多区域,对粒子由内向外分别赋予倍增的区域重要性,使其在区域边界分裂,可有效降低计算结果的统计误差[3]。
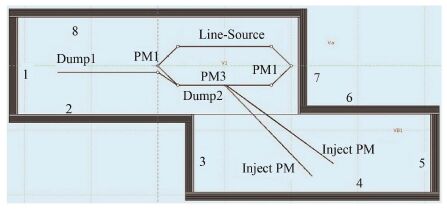
1.2 损失源项ERL-FEL装置简化结构如图 1所示。其中PM1/PM2/PM3以及Inject PM表示准直器的位置,Dump1和Dump2表示垃圾桶所在的位置。加速腔、支撑部件、调频器、冷却系统等加速器结构部件等用内径3 cm、厚度1 cm的铁圆柱管道代替,管道内填充真空;屏蔽层由1-8号墙以及顶板9部分组成,分别填充密度为2.27 g∙cm-3的混凝土。装置主要的束流损失点包括注入准直器(Inject PM)、Merger准直器(PM3)、环中准直器(PM1/PM2)、束流管线(Line-source)以及垃圾桶(Dump1和Dump2),其具体的束流损失率[1, 4]如表 1所示。
|
图 1 ERL-FEL装置的简化模型 Figure 1 Simplified model of the ERL-FEL. |
| 表 1 ERL-FEL 损失源项 Table 1 The lost sources of ERL-FEL. |
目前,FLUKA处理加速器多个损失源项的方法一般是首先以多个独立损失源项分开模拟,然后通过辅助软件对所有结果做累计处理[3]。本文采用离散抽样方式对加速器所有损失源项进行统一抽样,编写至一个FLUKA用户源程序Source.f中,进行加速器屏蔽厚度的设计。由于ERL和FEL是交叉运行的模式,故需要对ERL和FEL分别进行屏蔽设计。本文先对ERL的源项进行抽样编写可拓展的源项程序,再将其应用到FEL装置中。
对于任意离散型分布,服从式(1):
| $F\left( X \right)={{\Sigma }_{x<{{x}_{i}}}}{{P}_{i}}$ | (1) |
式中:F(X)为离散型分布函数;x1,x2,…为函数的跳跃点;P1,P2,…为相应的概率;
| ${{X}_{F}}={{X}_{I}}, \underset{i=1}{\overset{I-1}{\mathop \sum }}\,{{P}_{i}}\le \xi <\underset{i=1}{\overset{I}{\mathop \sum }}\,{{P}_{i}}$ | (2) |
式中:XF表示由已知分布F(X)中产生的简单子样的个体;ζ是属于[0, 1]的随机数。
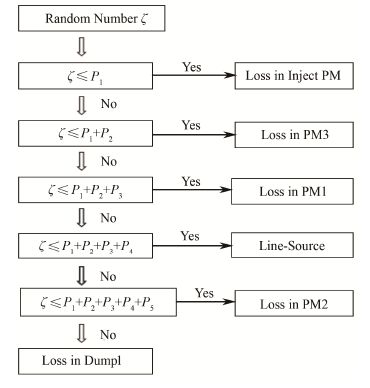
对应于ERL中的源项所构成的离散分布,Pi代表ERL各损失点处的损失率,其具体的抽样过程如图 2所示。对于点源情况,一次抽样决定其能量、方向等参数,对于线源,需要在一次抽样的基础上进行第二次均匀抽样。这样便可以实现多个点源和线源同时写入一个FLUKA源项程序。由于研究问题的角度不同,本文对准直器和束流管等模型进行了相应的简化。
|
图 2 ERL离散抽样过程 Figure 2 Discrete sample process of ERL. |
电子打在管壁上方向与束流中心的角度很小,约为1º,电子均匀打在管壁上。这时电子在1 cm厚管壁上走过的直线长度为1 cm/tan1º=57.47 cm,即等效靶的厚度为57.47 cm。均匀损失模型的抽样主要包括两个方面:一是电子出射方向的抽样,让损失的电子以束流方向成1º的发射角打在束流管上;二是电子的位置抽样,让损失的电子在一个与束流管侧面很接近的假想同轴圆柱面上均匀分布。通过函数FLRNDM产生一个0-1(不包括1)的浮点小数实现电子抽样。电子抽样物理学模型[5]如下:
位置抽样:
| $\left\{ \begin{align} & x={{R}_{0}}\cos (2\text{ }\!\!\pi\!\!\text{ }{{\varepsilon }_{1}}) \\ & y={{R}_{0}}\sin (2\text{ }\!\!\pi\!\!\text{ }{{\varepsilon }_{1}}) \\ & z={{z}_{1}}+{{\varepsilon }_{2}}({{z}_{2}}-{{z}_{1}}) \\ \end{align} \right.$ | (3) |
方向抽样:
| $\left\{ \begin{align} & u=\sin {{\theta }_{0}}\cdot \text{cos(}2\text{ }\!\!\pi\!\!\text{ }{{\varepsilon }_{1}}\text{)} \\ & v=\sin {{\theta }_{0}}\cdot \sin (2\text{ }\!\!\pi\!\!\text{ }{{\varepsilon }_{1}}) \\ & w=\cos {{\theta }_{0}} \\ \end{align} \right.$ | (4) |
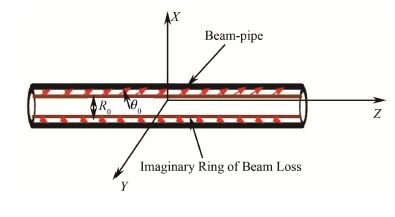
式中:(x,y,z)和(u,v,w)分别为抽样粒子的位置坐标和方向余弦;ε1为随机抽样参数;R0为抽样粒子所在处假想圆柱面半径;z1、z2为束流管两端的轴向坐标;θ0是抽样粒子的发射角。
|
图 3 束流线源模型 Figure 3 Simplified model of the beam tube model. |
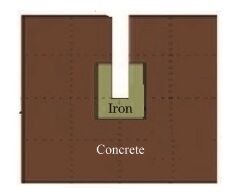
由于空间的限制,本项目的垃圾桶的设计是埋在地下,其剖面示意图如图 4所示。
|
图 4 垃圾桶的简化模型 Figure 4 Simplified model of the beam dump. |
垃圾桶主要由铁靶以及包裹在外的混凝土构成,束流垂直打在垃圾桶中,如图 1中Dump1和Dump2所示,垃圾桶埋放在所示位置地下0.5 m处。
1.6 准直器模型准直器模型的机器结构比较复杂,每个准直器的主体结构也基本相同,均由一对水平和垂直方向的束流刮片、通过调节连杆与束流刮片相连的铜散热片、包围束流刮片和束流管的铁屏蔽、以及周围铁屏蔽的外部混凝土屏蔽组成[6]。为简化准直器的模型,采用点靶替换法的模型来处理,在考虑主体墙的屏蔽时暂不考虑准直器局部屏蔽。具体思路是:让电子恰好通过一定厚度的钨靶。对于注入准直器和Merger准直器对应的电子能量为5 MeV,对于环中准直器对应能量为35 MeV,利用1-100 MeV电子在不同物质中的射程拟合公式[6]计算相应的钨靶厚度:5 MeV对应的靶厚度为1.65 mm,35 MeV对应的靶厚度为7.98 mm。
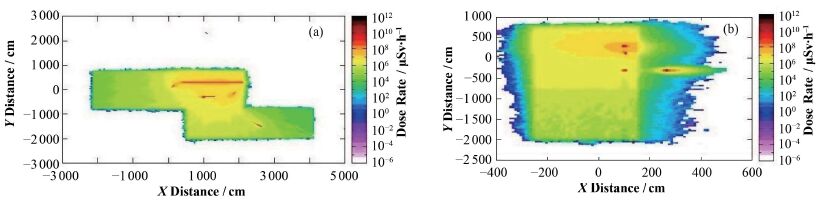
2 结果分析及应用 2.1 结果分析 2.1.1 整体源项程序与各源项独立处理后累积结果的剂量分布图对比当墙体外加有1.5 m的混凝土屏蔽时,利用flair软件分别获得从不同方向投影的等效剂量分布如图 5所示。这里的剂量是直接利用USRBIN卡的DOSE-EQ参数获得的等效剂量,包括光子以及中子的总剂量。
|
图 5 ERL等效剂量分布图 (a) Z方向投影,(b) X方向投影 Figure 5 Equivalent dose distribution of ERL. (a) From Z,(b) From X |
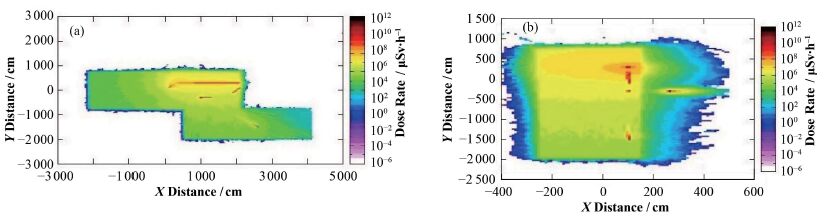
利用以往的方法,进行模拟时,从每个束流损失源项出发,通过模拟得到各自的剂量结果,然后将结果进行合并处理,得到的剂量分布如图 6所示。
|
图 6 ERL等效剂量分布图 (a) Z方向投影,(b) X方向投影 Figure 6 Equivalent dose distribution of ERL. (a) From Z,(b) From X |
由图 6可知,每个束流损失点所造成的剂量分布都可以很清楚地呈现在同一剂量分布图中,并且整体源项程序与各源项独立处理后累积结果的剂量分布的结果基本一致。
2.1.2 整体源项程序与各源项独立处理后累积结果的剂量数值对比取原有墙体厚度(0.3 m)屏蔽时获得1号、4号、7号、8号墙体屏蔽后方的等效剂量的结果如表 2所示,两者的计算结果基本都维持在同一数量级,数值上也只存在细微的差别。
| 表 2 ERL屏蔽计算结果比较 Table 2 The comparison of the shielding results. |
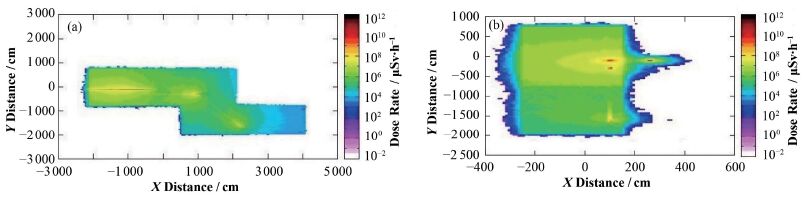
对于FEL部分,抽样方法同理,只需要修改source.f中损失源项的损失比例参数,包括束流损失的位置、方向、能量以及点源或线源抽样的选择。由此得出FEL的剂量分布如图 7所示。
|
图 7 FEL等效剂量分布图 (a) Z方向投影,(b) X方向投影 Figure 7 Equivalent dose distribution of FEL. (a) From Z,(b) From X |
由上分析可知,在加速器屏蔽优化设计中,利用离散抽样的方法对多个损失源项进行整合,在同一FLUKA用户程序Source.f中实现多源抽样的方法是可行的,此方法可拓展应用到其它加速器的防护设计,特别是针对医用、工业等加速器防护设计中空间小、损失源项过多的情况,有一定参考价值。
| [1] |
崔小昊. ERL-FEL两用实验装置设计及相关动力学研究[D]. 北京:中国科学院高能物理研究所, 2013.
CUI Xiaohao. Lattice design and beam dynamics study of ERL-FEL test-facility at IHEP[D]. Beijing:Institute of High Energy Physics, Chinese Academy of Sciences, 2013 (  0) 0)
|
| [2] |
徐玉海, 夏晓彬, 王光宏, 等. 基于束流线源模型自由电子激光器主体墙的屏蔽设计[J].
核技术, 2014, 37 (6) : 060101 .
XU Yuhai, XIA Xiaobin, WANG Guanghong, et al. Shielding design of free electron laser's main wall based on the line-source sampling physical model[J]. Nuclear Techniques, 2014, 37 (6) : 060101 . DOI: 10.11889/j.0253-3219.2014.hjs.37.060101 (  0) 0)
|
| [3] |
吴青彪. 中国散裂中子源感生放射性研究[D]. 北京:中国科学院高能物理研究所, 2014.
WU Qingbiao. Study on induced radioactivity of China spallation neutron source[D]. Beijing:Institute of High Energy Physics, Chinese Academy of Sciences, 2014 (  0) 0)
|
| [4] |
Matsumura H, Hozumi K, Haga K, et al. Design for radiation protection of compact ERL in KEK[R]. Tsukuba:KEK, 2013
( 0) 0)
|
| [5] |
马忠剑. CSNS辐射场分析及中子剂量探测技术研究[D]. 北京:中国科学院高能物理研究所, 2010.
MA Zhongjian. Analysis of CSNS radiation field and research on detection of neutron dose equivalent[D]. Beijing:Institute of High Energy Physics, Chinese Academy of Sciences, 2010 (  0) 0)
|
| [6] |
邵文成. 医用电子直线加速器辐射防护和质量控制的Monte Carlo方法研究[D]. 哈尔滨:黑龙江大学, 2009.
SHAO Wencheng. The Monte Carlo method uesd in radiation protection and quality control of medical electron linear accelerator[D]. Harbin:Heilongjiang University, 2009 (  0) 0)
|
