波荡器在辐射同步光的同时，也会影响束流的稳定运行。波荡器磁场沿直线的一、二次积分会引起束流运动轨道的闭轨畸变；积分场的四极分量会对束流产生聚/散焦作用，引起束流工作点漂移(Tune Shift)、耦合度(Coupling)和束斑尺寸改变等；积分场六极和八极等高阶分量会产生复杂的束流非线性效应，减少动力学孔径和缩短束流寿命等。一、二次积分场及其高阶分量可以通过霍尔(Hall)点测或者积分线圈测量得到，可通过波荡器端部校正线圈和“Magic Fingers”小磁柱排列等来补偿。

波荡器动力学积分场是指磁场沿运动电子轨迹的积分，会引起束流工作点漂移、动力学孔径减少和束流寿命缩短等，其效应反比于电子能量的平方，正比于波荡器周期长度的三次方和波荡器磁场的横向不均匀性。“APPLE (Advanced Planar Polarized Light Emitter)-Ⅱ”型可变椭圆极化波荡器(Elliptically Polarized Undulator,EPU)因其不仅能产生线极化光，还能产生各种椭圆极化光，越来越多的在同步辐射装置中研制应用，但其磁结构本身会产生严重的磁场横向不均匀性，尤其是对于垂直线极化模式，其动力学积分场效应及其磁场垫补方法是国际粒子加速器领域的研究热点。

为上海光源(Shanghai Synchrotron Radiation Facility,SSRF)超高分辨宽能段光电子实验线站（简称“梦之线”）研制的发光源是一台双椭圆极化波荡器(Double EPU,DEPU)，包括两台“APPLE-Ⅱ”型可变椭圆极化波荡器，总长度都接近5 m，共用一个“H”形机架，此机架可横向移动从而实现两台波荡器间的切换，其主要设计参数见表 1。使用“Kick-Map”^[1]方法研究了DEPU波荡器动力学积分场对上海光源束流的影响^[2]，计算结果表明，波荡器EPU58在所有工作极化模式和工作磁气隙下，对束流工作点漂移的最大影响小于0.004，这对于储存环束流的稳定运行来说是可以接受的；波荡器EPU148在最小磁气隙垂直线极化模式下对束流工作点漂移的影响最大，最大漂移量大于0.01，这对于储存环束流的稳定运行来说是不可以接受的，需采取措施来减少波荡器动力学积分场对束流的影响。

表 1

表 1 DEPU主要设计参数 Table 1 Main parameters for DEPU EPU58 EPU148 周期长度Periodlength / mm 58 148 周期数Periodnumber 84 32 磁结构Magneticstructure APPLE-Ⅱ APPLE-Ⅱ 最小磁气隙Minimumgap / mm 16.5 22 水平线极化最大有效磁场Maximumeffective field at H.P. Mode / T >0.78 >0.67 圆极化最大有效磁场Maximumeffective field at C.P. Mode / T >0.44 >0.45 磁铁总长Totallength / m ~5 ~4.9 线极化光子能量范围Photonenergy rang at L.P. Mode / eV 200-2000 20-200 圆极化光子能量范围Photonenergy rang at C.P. Mode / eV 300-2000 20-300

表 1 DEPU主要设计参数 Table 1 Main parameters for DEPU

通过调整波荡器附近(Local)四极磁铁或者全环(Global)四极磁铁的磁场强度可以前馈补偿动力学积分场对束流的影响。对于不同位置入射的电子由波荡器动力学积分场引起的聚焦效应是不同的，四极磁铁前馈对于储存环“Top-up”运行时电子的偏轴注入，不能很好地补偿。波荡器动力学积分场在不同的磁气隙和不同的极化模式下对束流的聚焦作用是不同的，需要大量的机器研究工作来得到四极磁铁的两维前馈电流表，对于波荡器在某一特定参数下运行时，插值得到其需要前馈的电流值。

降低波荡器磁场的横向不均匀性能有效减小动力学积分场对束流的影响，为提高“APPLE-Ⅱ”型可变椭圆极化波荡器的磁场横向均匀性，前人提出了几种方法^[3-4]。例如，垂直磁化永磁块的充磁方向有一定偏角，永磁块靠近束流的平面改为斜面或者曲面等。这些方法或者增加了磁化块的加工难度和充磁误差，或者限制了波荡器的磁气隙大小、牺牲峰值磁场强度等。

通过局部磁场垫补来补偿动力学积分场效应将减少繁琐的机器研究工作、不牺牲峰值磁场强度和不增加波荡器磁化块的加工难度。欧洲同步辐射光源(European Synchrotron Radiation Facility,ESRF)实验室的Chavanne提出了“L-Shimming”垫补方法^[5]，其产生的额外磁场能在“APPLE-Ⅱ”型可变椭圆极化波荡器不同的磁气隙、不同的极化模式和不同的电子入射位置对束流产生不同的聚焦作用，来抵消波荡器动力学积分场对束流的影响。该垫补方法是通过在可变椭圆极化波荡器永磁块磁排列上粘贴软磁材料来实现的，软磁垫片放置在永磁块的靠近波荡器中心轴的两个平面上，其纵向中心位置一般位于垂直磁化永磁块上，如图 1所示。

图 1

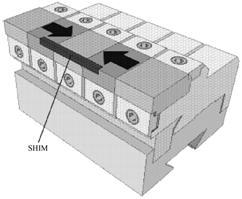
图 1 “L-Shimming”垫补示意图 Figure 1 Sketch map of “L-Shimming”.

以波荡器EPU148为例，使用RADIA Code建模计算，研究了“L-Shimming”垫补的原理。模拟计算的软磁垫片长宽厚分别为37 mm×5 mm× 0.5mm，纵向中心位置位于垂直磁化的永磁块上。

在水平线极化模式下，磁排列间没有相位移动，假设“L-Shimming”垫片位于不同磁排列的磁化方向朝下的永磁块上，如图 2所示，模拟计算最小磁气隙22 mm下不同磁排列上垫补产生的水平和垂直磁场沿纵向积分在波荡器中平面上的分布如图 3所示，图 3(b)中1#与4#重合、2#与3#重合，积分范围为垫片产生额外磁场的所有分布范围。没有“L-Shimming”垫片时，理想波荡器由于磁结构的上下对称性，磁力线垂直于中平面，在中平面上只有垂直磁场，没有水平磁场；增加垫片后，破坏了磁结构的对称性，磁力线分布发生改变，在中平面上产生额外的垂直和水平磁场。

图 2

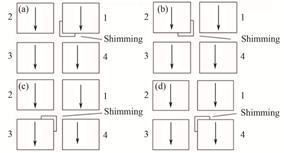
图 2 水平线极化模式“L-Shimming”在不同磁排列上 Figure 2 “L-Shimming” at different magnetic column in horizontal linear polarization mode.

图 3

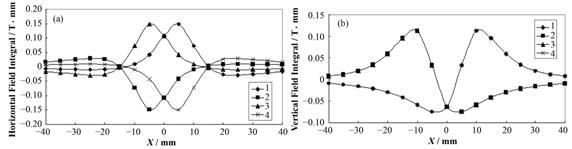
图 3 水平线极化模式下“L-Shimming”放置在不同磁排列上产生的水平(a)和垂直(b)磁场积分 Figure 3 Horizontal (a) and vertical (b) field integral distribution for “L-Shimming” at different magnetic column in horizontal linear polarization mode.

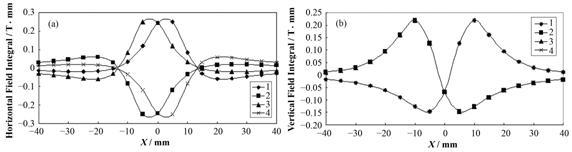
在垂直线极化模式下，对角线磁排列间的相位移动距离为波荡器周期长度的一半，假设“L-Shimming”垫片在水平线极化模式位于不同磁排列的磁化方向朝下的永磁块上，切换到垂直线极化模式下，垫片感受到的磁场环境如图 4所示。模拟计算最小磁气隙下不同磁排列上垫片产生的水平和垂直磁场沿纵向积分在波荡器中平面上分布如图 5所示，图 5(b)中1#与4#重合、2#与3#重合，与水平线极化模式类似，理想波荡器由于磁结构左右对称，磁力线垂直于波荡器中心竖直平面，在中平面上只有水平磁场，没有垂直磁场，增加垫片后，破坏了磁结构的对称性，磁力线分布发生改变，在中平面上产生额外的垂直和水平磁场。

图 4

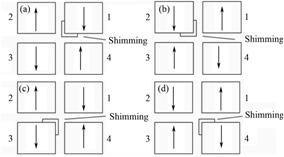
图 4 垂直线极化模式“L-Shimming”在不同磁排列上 Figure 4 “L-Shimming” at different magnetic column in vertical linear polarization mode.

图 5

图 5 垂直线极化模式下“L-Shimming”放置在不同磁排列上产生的水平(a)和垂直(b)磁场积分 Figure 5 Horizontal (a) and vertical (b) field integral distribution for “L-Shimming” at different magnetic column in vertical linear polarization mode.

在上述两种线极化模式下，磁场积分的强度不同，磁场积分分布随垫片在不同磁排列上的变化规律相同：垫片在四排磁排列上产生的水平磁场积分分布分别关于水平坐标轴和垂直坐标轴两两对称；垫片在1#(2#)和4#(3#)磁排列上产生的垂直磁场积分分布相同，并且1#与2#磁排列上产生的垂直磁场积分分布关于垂直坐标轴对称。如果把垫片在四排磁排列上产生的磁场叠加，那么水平磁场积分在中平面上为零，垂直磁场积分在束流中心线上不为零，关于垂直坐标轴对称，但是“APPLE-Ⅱ”型可变椭圆极化波荡器动力学积分场在束流中心线上为零，并且在中平面上垂直磁场积分（水平偏角）关于垂直坐标轴反对称，也就是说把垫片放置在磁化方向相同（都朝下或都朝上）的垂直磁化永磁块上，四排磁列上产生的垫补磁场叠加不能补偿动力学积分场效应。

由于对称性，“L-Shimming”垫片放置在相同的磁排列而磁化方向不同的磁化块上，产生的水平和垂直磁场积分符号将相反。如果1#和4#磁排列上的垫片中心放置在磁化方向朝下的永磁块上而2#和3#磁排列上的垫片中心放置在磁化方向朝上的永磁块上，则这样一组垫片在波荡器中平面上产生的水平磁场积分为零，垂直磁场积分在束流中心线上为零且关于垂直坐标轴反对称，这样的4个不同位置垫片定义为一个“标准垫片组”。从图 3(b)和图 5(b)的结果进一步计算可以发现：“标准垫片组”在电子不同入射位置产生的垂直积分场梯度不同，在不同极化模式下垂直磁场积分和积分场梯度不同。可以预见，“标准垫片组”在中平面上产生的垂直磁场积分和积分场梯度将随着磁气隙的增加而减小。波荡器动力学积分场也随不同入射位置、不同极化模式和不同磁气隙而变化，优化设计“标准垫片组”垫片的尺寸，可有效补偿波荡器动力学积分场效应。如果一组“标准垫片组”产生的积分场强度不够，可通过多组来实现。

波荡器动力学积分场引起的电子偏角与电子能量的平方成反比^[1]，而“L-Shimming”垫片产生的磁场积分引起的电子偏角与电子能量成反比。“L-Shimming”的垫补设计只能是针对特定的电子能量，如果电子能量发生改变，垫补不能再有效抵消动力学积分场效应。同步辐射光源储存环的电子能量一般是恒定的，可不考虑“L-Shimming”垫补对于电子能量的依赖性。

通过模拟计算波荡器EPU148在不同磁气隙下和不同相位移动距离下的磁场分布，使用“Kick-Map”方法计算得到了“L-Shimming”垫片组在波荡器中平面上不同横向位置需提供的积分四极磁场强度。计算结果表明，在最小磁气隙垂直线极化模式下需要提供的积分四极磁场强度最大。

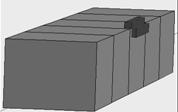
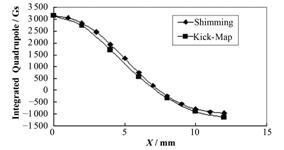
使用“RADIA Code”^[6]模拟计算，优化设计了波荡器EPU148 “L-Shimming”垫片的尺寸和安装位置，以最小磁气隙垂直线极化模式下需要补偿的积分四极磁场强度作为目标函数兼顾其它极化模式和磁气隙下需要的补偿量。垫片选用武钢出厂牌号为J23-G50的矽钢片材料，优化设计的方案采用两片厚度不同的垫片，如图 6所示，水平垫片长、宽、高为29.6mm×2.4mm×2mm，垂直垫片长、宽、高为29.6mm×3 mm×1.5 mm。只使用了一组“标准垫片组”，垫补积分场强度就达到了需求。优化设计的垫补方案在波荡器EPU148最小磁气隙垂直线极化模式下模拟计算产生的积分四极磁场强度与需要提供的垫补量对比如图 7所示。从图 7中可以看出，两者基本一致，优化设计的垫补方案能有效抵消波荡器动力学积分场对束流的影响。

图 6

图 6 波荡器EPU148 “L-Shimming”垫补 Figure 6 “L-Shimming” in EPU148.

图 7

图 7 EPU148在最小磁气隙垂直线极化模式下优化设计的垫补结果 Figure 7 Shimming result of optimized design for EPU148 at minimum gap in vertical linear polarization mode.

根据波荡器EPU148在储存环中的安装方位和需要补偿的积分四极磁场的聚散焦性，确定在不同磁排列上放置垫片的永磁块的上下磁化方向。垫片使用环氧树脂胶粘贴在磁化块表面，放置在靠近波荡器端部的常规周期永磁块上，以尽量减少对辐射光特性的影响。

在波荡器EPU148磁场垫补前后，使用翻转长线圈(Flipping Coil)测量得到中平面上磁场一次积分的分布，从而得到垫片实际产生的积分磁场垫补量。

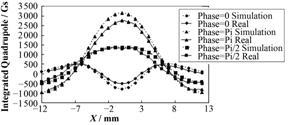
波荡器EPU148在最小磁气隙不同相位移动距离下的垫补磁场实际测量结果与模拟计算结果的比较见图 8。从图 8中可以看出，两者基本一致，在相位移动距离74 mm (Phase=π)，波荡器束流中心线上的误差最大，约为300 Gs，相当于模拟计算的需要提供的最大垫补量的10%，垫补后动力学积分场效应对束流的工作点的影响将减少一个数量级。

图 8

图 8 波荡器EPU148在最小气隙不同相位移动距离下垫补磁场实测值与模拟计算值的比较 Figure 8 Comparison of measured shim result with simulation for EPU148 at minimum gap in different phase shift.

垫片模拟计算得到的积分四极磁场强度与实际磁场测量结果的区别，可能是由以下原因造成的：

1) 翻转线圈测量误差；

2) 模拟计算的磁化曲线与实际材料磁化曲线的区别；

3) 垫片的加工尺寸误差；

4) 垫片的安装位置误差等。

波荡器EPU148装入上海光源储存环后，机器研究了其对束流的影响。波荡器EPU148在不同磁气隙和不同相位移动距离下机器研究的结果见表 2、3。可见，波荡器运行在所有工作磁气隙和相位移动距离下，引起的工作点漂移都小于0.001，对束流注入效率基本上没有影响，这也证明了动力学积分场效应垫补是成功的。

表 2

表 2 EPU148运行在水平线极化模式不同气隙下的束流工作点和注入效率 Table 2 The tune and injection efficiency with EPU148 in horizontal linear polarization mode at different gap. 气隙 Gap / mm 工作点 Tune (Qx/Qy) 注入效率 Injection efficiency / % 118 22.219/11.299 88 90 22.219/11.299 89 70 22.219/11.299 87 50 22.219/11.300 86 40 22.22/11.300 87 30 22.22/11.300 90 22 22.221/11.301 88

表 2 EPU148运行在水平线极化模式不同气隙下的束流工作点和注入效率 Table 2 The tune and injection efficiency with EPU148 in horizontal linear polarization mode at different gap.

表 3

表 3 EPU148运行在最小气隙不同极化模式下的束流工作点和注入效率 Table 3 The tune and injection efficiency with EPU148 at minimum gap in different polarization mode. 相位 Phase shift / mm 工作点 Tune (Qx/Qy） 注入效率 Injection efficiency / % 74 22.219/11.301 85 60 22.219/11.301 85 50 22.219/11.301 88 40 22.220/11.301 84 30 22.220/11.301 86 20 22.220/11.301 85 10 22.221/11.300 86 0 22.221/11.301 88 -10 22.221/11.300 88 -20 22.221/11.301 87 -30 22.220/11.301 89 -40 22.220/11.301 84 -50 22.219/11.301 90 -60 22.219/11.301 86 -74 22.219/11.301 86

表 3 EPU148运行在最小气隙不同极化模式下的束流工作点和注入效率 Table 3 The tune and injection efficiency with EPU148 at minimum gap in different polarization mode.

本文研究了减少可变椭圆极化波荡器动力学积分场效应的磁场垫补方法。以波荡器EPU148为例模拟计算，系统研究了“L-Shimming”磁场垫补原理。使用RADIA Code模拟计算优化设计了波荡器EPU148动力学积分场效应垫补的垫片尺寸和安装位置。翻转线圈磁测结果表明实际测量得到的垫补磁场强度与模拟计算磁场强度基本一致，误差小于最大垫补量的10%，垫补后动力学积分场对束流的影响将减少一个数量级。波荡器EPU148机器研究结果证明了其动力学积分场效应的垫补是成功的。