2. 中国科学院大学 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
巴西Sirius光源是巴西政府投资建设的第三代同步辐射光源,其电子储存环周长518.2 m,电子能量3.0 GeV,束流发射度0.28 nm∙rad,是目前国际上正在建设的两台超低发射度储存环之一。工程首期由直线加速器、增强器、储存环和13条光束线组成,其中巴西Sirius光源直线加速器整机工程项目由中国科学院上海应用物理研究所承建,应物所将以“交钥匙”项目形式为Sirius光源提供一台电子直线加速器,主要项目内容包括设计、制造、安装、调试和交付。该项目将借鉴上海光源直线加速器设计、建造和运行经验,结合近几年加速器技术发展,对部分系统和设备设计进行优化和升级,以实现高性能、长期稳定运行目标。
作为该工程项目的一个重要组成部分,本文研究和实现了一个通用、鲁棒、高效、可扩展性好的电子直线加速器低电平控制系统。该系统基于MicroTCA,采用添加了控制算法库的EPICS (Experimental Physics and Industrial Control System)架构,欲实现的控制功能包括自动频率控制(Automatic Frequency Control,AFC)、前馈控制(速调管线性化,矢量调制器校准,束流负载的补偿)、基于束流的反馈控制。目前AFC的工作已经完成,能够采用两种不同的方法,利用PID (Proportion- Integral-Differential)算法,进行频率自动控制。在巴西Sirius光源直线加速器实验装置上对该系统进行调试和测试,观测性能表现,测得实验数据。结果表明,两种不同的AFC方法都是有效的,证明所采用的控制方案和软件架构都是可行的。分析所得结果,以便进一步优化。由于可扩展性好,将会有更多算法库添加到该控制系统,以实现更多控制功能,整个控制系统将会更加完善和优质。
值得一提的是,虽然该控制系统是巴西Sirius光源直线加速器整机工程项目的一部分,但通用性、可移植性、可扩展性在整个研发环节都有考虑。因此,该控制系统可移植到其它电子直线加速器上,例如,正在建设的上海软X射线自由电子激光装置,从而节省人力财力,提高效率。
1 Sirius光源直线加速器直线加速器作为注入器,其性能表现直接影响到束流品质,进而影响同步辐射光的品质。Sirius光源直线加速器主要技术指标如表 1所示。该直线加速器的组成类似于上海光源直线加速器,主要由电子源(电子枪)系统、纵向聚束系统、加速结构段、功率源和控制系统组成[1]。其中,纵向聚束系统包括一个次谐波聚束器和一个基波聚束器,这是由于电子枪是热阴极栅控高压电子枪,需要把相对于基波6倍相宽的电子相聚到一个基波中去产生较高的流强,从而减小电子枪的压力,保证低发射度和能散[2]。次谐波聚束器为重入式驻波腔,由于外界温度、机械振动等噪声的干扰,次谐波聚束器的谐振频率会发生改变。另外,储存环周长会因为温度或地基等而改变,电子沿环运动一圈所经过的路程由高频频率决定。如果储存环周长发生变化而高频频率保持不变,会在水平方向产生一个正比于色散函数的轨道畸变。由周长和频率不匹配产生的闭轨畸变只能通过调整高频频率加以校正[3]。因此,次谐波聚束器会时常处于失谐状态,最终导致高频腔体内的场强不稳定,引起束流的振荡[4],对直线加速器的束流传输效率、束流强度和品质会有很大的影响。基于MicroTCA的AFC系统就是通过反馈控制环路,利用相关原理及算法,避免次谐波聚束器失谐,进而稳定幅度、相位,保证直线加速器长期稳定可靠运行。
| 表 1 Sirius光源直线加速器主要技术指标 Table 1 Main parameters of Sirius-LINAC. |
我们选用的低电平控制器为MicroTCA,它亦称为MTCA (Micro Telecommunications Computing Architecture),是PICMG协会(PCI工业计算机制造业联盟,PCI Industrial Computer Manufacturer’s Group)在2007年向外界公开发布的一种标准构架。它既继承了ATCA的所有优点,又吸收了cPCI总线和VXI总线的长处,将各个功能模块彼此分开,相互独立,提高了硬件的利用效率,利于系统的维护和升级。MicroTCA已经在德国电子同步加速器(German Electron Synchrotron,DESY)、欧洲X射线自由电子激光装置(The European X-ray Free- Electron Laser,European XFEL)、斯坦福直线加速器中心(Stanford Linear Accelerator Center,SLAC)以及高能加速器研究机构(High Energy Accelerator Research Organization,KEK)等实验室充分应用,且表现优异[5]。经过综合考虑,MicroTCA为最优方案,它既可以提供稳定的、高精度的控制,又便于操作、维护和升级。
MicroTCA系统的关键组件包括:MicroTCA机箱、MCH (MicroTCA Carrier Hub)、AMC (Advanced Mezzanie Card)、RTM背板(Rear Transition Module)以及电源模块(Power Module)。我们采用的AMC是SIS8300L2,它是低电平控制器的核心,包括10路AD(AD9268) 和2路DA(MAX5878) ,分辨率为16位,采样频率分别达到125 MHz和250 MHz,完成微波信号的采集和数字化反馈控制的运算处理,输出基带正交信号IQ;RTM背板为DWC8VM1,它作为RF前端,包括8路RF信号的下变频,2路直接中频采样,1路基带信号的上变频,带宽700-4000MHz,并含有矢量调制器,将SIS8300L的DAC输出的IQ信号与参考信号混频,得到具有合适的幅度和相位的RF信号。
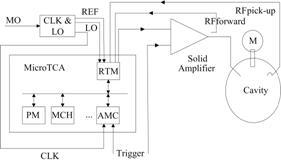
MO信号、LO信号和IF信号的频率分别为499.658 MHz、474.128 MHz和25.5 MHz,采样率是102 MHz。放大器、分频器、混频器等频率合成的关键器件选用了低噪音的器件,以提高输出的信噪比。硬件架构如图 1所示。
|
图 1 硬件架构图 Figure 1 Hardware architecture diagram. |
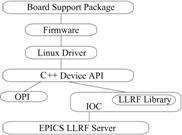
在软件架构方面,我们借鉴DESY的MTCA4U (MicroTCA.4 User tool kit)的优点和长处[6],将软件层次化、模块化、接口化,彼此独立但又紧密联系,便于扩展、调试、维护和升级。考虑到实际情况,最终得到如图 2所示的软件架构。我们采用的是EPICS控制系统架构,因为它是基于分布式控制体系“标准模型”结构,具有分布式、开放、易扩充、多平台等优点[7]。EPICS由监控层、过程控制层和设备控制层三个层次组成,分别称作操作员接口计算机(Operator Interface,OPI),输入/输出控制器(Input/output Controller,IOC),设备控制器(Device Controller)。
|
图 2 软件架构图 Figure 2 Software architecture diagram. |
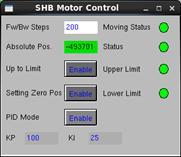
系统中的Firmware由VHDL语言实现,IOC由C和C++编写,OPI采用EDM实现。控制调谐步进电机的OPI界面如图 3所示。实现AFC等控制功能的程序在LINUX环境下采用C语言开发,全部采用标准数据结构和算法库,以满足跨平台、便于移植、通用性好等要求。控制算法程序是整个系统的核心,通过接口以算法库的形式被IOC调用,嵌入控制系统,成为系统独立但又重要的一部分,实现控制功能,同时也便于调试和未来的优化扩充。
|
图 3 电机控制OPI界面 Figure 3 OPI for SHB motor control. |
总体来说,整个控制系统的运行环境为LINUX操作系统,在EPICS框架下完成对FPGA (Field Programmable Gate Array)数字处理板卡的控制,实现AFC及微波幅度相位的反馈控制等控制功能,实现信号的监测,并响应监控层或其他IOC的请求,处理来自设备控制层的外部事件等。
4 AFC原理及算法频率调谐分为快调和慢调,由于导致次谐波聚束腔失谐的是温度变化等慢变化的噪声,所以只考虑慢调。温度的变化导致次谐波聚束腔形状改变,其谐振频率和输出反馈信号的幅度和相位也会随之改变。通过耦合器探测次谐波聚束腔的输入信号RFforward和反馈信号RFpick-up,分别通过调谐环路器件和场反馈环路器件输入给低电平控制器。IOC中的AFC程序获取需要的信息,通过两种不同方法计算次谐波聚束腔的频率失谐量,再利用PID算法,输出一个控制量给驱动器,驱动步进电机旋转相应的步数,步进电机经丝杆螺母传动链拖动调谐杆,调谐杆的伸缩补偿了次谐波聚束腔由于噪声而导致的形变,从而实现AFC。为保护系统,我们采用光电限位开关保证调谐器的位置不超出范围。
4.1 利用失谐相角的方法腔体失谐后,输出反馈信号RFpick-up的相位也会发生改变,输入信号RFforward和反馈信号RFpick-up的相位差即为失谐相角。由于失谐相角y和频率失谐量Δf之间存在如下关系[8]:
| $\tan \psi =2{{Q}_{L}}\frac{\Delta f}{f}$ | (1) |
因此,可通过鉴别RFforward和RFpick-up信号相位的方法,得出腔体频率失谐量,进而利用PID算法得到调节量,驱动步进电机,进行腔体调谐,这是第一种AFC的原理和过程。
4.2 利用RF Decay的方法对于工作在脉冲模式下的驻波腔,可利用脉冲衰减(RF Decay)计算出频率失谐量。研究这一方法具有特殊意义,因为在某些情况下,不能用第一种方法进行调谐,例如上海软X射线自由电子激光装置中的SLED[9]的调谐。
高频腔的物理和电学特性和并联RLC电路相似,因此,RF Decay期间的高频腔等效于RLC并联电路放电过程。经过简单的分析和公式推导,可知,RF Decay期间RFpick-up的相位随时间线性变化,换言之,RF脉冲结束会引起RFpick-up频率的跳变,导致相位随时间的线性变化[10]。即RF Decay期间的RFpick-up相位θ和时间t存在如下关系:
| $\theta \text{=}b+\Delta \omega \cdot t$ | (2) |
因此,在RF Decay期间采集一定数目的样本点,个数用n表示,初步选为脉冲关闭后的16 μs开始的50个数据。用最小二乘法进行线性拟合[10],即可求得腔体失谐信息Δω:
| $\Delta \omega \text{=}\frac{n\sum\limits_{i=0}^{n-1}{\left( {{\theta }_{i}}\cdot {{t}_{i}} \right)-\sum\limits_{i=0}^{n-1}{{{t}_{i}}\cdot \sum\limits_{i=0}^{n-1}{{{\theta }_{i}}}}}}{n\sum\limits_{i=0}^{n-1}{{{t}_{i}}^{2}}-\sum\limits_{i=0}^{n-1}{{{t}_{i}}\cdot \sum\limits_{i=0}^{n-1}{{{t}_{i}}}}}$ | (3) |
进而可得:
| $\Delta f\text{=}\frac{1}{2\text{ }\!\!\pi\!\!\text{ }}\Delta \omega $ | (4) |
| $\psi ={{\tan }^{-1}}2{{Q}_{L}}\frac{\Delta f}{f}$ | (5) |
求得频率失谐量后,利用PID算法得到调节量,驱动步进电机,进行腔体调谐,这是第二种AFC的原理和过程。
4.3 PID算法我们采用PID算法作为控制算法。该算法按偏差的比例(P)、积分(I)和微分(D)进行控制,具有原理简单、易于实现、适用面广、控制参数相互独立、参数的选定比较简单等优点。微分(D)起预测将来误差的作用,但对噪声变化很敏感,实际中的速度缓慢的系统可以不需要微分(D),所以我们最终采用PI算法。
若u(t)定义为控制输出,PI算法可用式(6) 表示:
| $u(t)={{K}_{p}}[e(t)+\frac{1}{{{T}_{l}}}\int_{0}^{l}{e(t)\text{d}t}]$ | (6) |
将式(6) 离散化,便可得到数字PI表达式[11]:
| $u(k)\text{=}{{K}_{\text{p}}}\left[ e(k)+\frac{{{T}_{s}}}{{{T}_{l}}}\sum\limits_{j=0}^{k}{e(j)} \right]$ | (7) |
由于要对巴西Sirius光源直线加速器的电子枪、次谐波聚束腔进行老练,对束测系统和控制系统进行调试评估,借此机会,我们在巴西Sirius光源直线加速器实验装置对AFC系统进行调试和测试,观测其性能表现,测得实验数据。
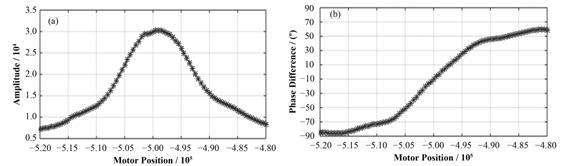
首先进行了电机调谐标定,在RFpick-up信号的幅度出现最大值,输入信号RFforward和反馈信号RFpick-up的相位差出现最小值时标定为谐振状态。然后通过OPI改变电机的位置,测得次谐波聚束腔的幅度和相位差谐振曲线,如图 4所示。
|
图 4 次谐波聚束腔的幅度(a)和相位差(b)谐振曲线 Figure 4 Resonance curves for amplitude (a) and phase difference (b) of the cavity. |
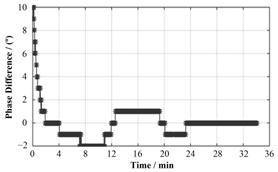
在第一种AFC方法的模式下,利用实验凑试法进行参数整定,最终选定P增益为25,I增益为8。在第二种AFC方法的模式下,尝试用4:1衰减曲线法进行参数整定[12],确定P增益为70,I增益为1,为测得阶跃响应曲线,人为调节步进电机的位置,使得产生约10的失谐相角,最终测得如图 5所示的响应曲线。
|
图 5 Kp=70、Ki=1时的阶跃响应曲线 Figure 5 Step response curve when Kp=70,Ki=1. |
为观测AFC系统长期稳定性,尤其是对温度变化噪声的抵抗能力,我们分别在关闭AFC系统、第一种AFC模式、第二种AFC模式三种不同情形下,利用恒温水箱,让次谐波腔的温度由室温(25 C)升至设定温度(45 C),维持该温度1 h左右,再关闭恒温水箱,让次谐波聚束腔自然降温,测得整个过程的失谐相位差如图 6所示。

|
图 6
三种不同情形下的失谐相位
(a) 没有使用AFC,(b) 第一种AFC模式, (c) 第二种AFC模式 Figure 6 Phase difference under three situations. (a) Without AFC,(b) First AFC mode,(c) Second AFC mode |
因为打火,所以图 6中有许多细小尖锐的毛刺,如图 6(b)表现得尤为明显。总的来说,AFC系统能很好地实现自动调谐功能,尤其是第一种方法,能将失谐相角控制在±1.5°以内,而且响应很快,所以线条密集;第二种方法也能起到调谐作用,但效果一般,只能将失谐相角控制在±4°以内,且响应较慢。分析原因,有以下几点:PI的参数整定还不够理想,RF Decay期间选取样本点的位置及个数的选择不够好,有其他的噪声的干扰,算法也不够高效,以上为优化工作的重点。AFC系统的正常工作证明我们所采用的控制方案和软件架构都是切实可行的。
6 结语高频腔失谐是常出现的一个问题,AFC系统能够利用两种不同方法实现自动频率调谐,经实际测试,能有效解决这一问题。本系统基于MicroTCA,采用EPICS架构,开发过程中充分考虑了通用性、可移植性、可扩展性,将来可以移植到其它电子直线加速器上,例如,正在建设的上海软X射线自由电子激光装置,从而节省人力财力和提高效率。对于系统中不够完善的地方,将会进一步优化。由于可扩展性好,未来将会有更多算法库添加到该系统,实现更多控制功能,而绝非仅限于AFC,整个控制系统将会更加完善和优质,更有利于获得高品质的电子束流。
| [1] |
赵明华, 林国强, 钟少鹏, 等. 上海光源150. MeV电子直线加速器的设计与调试[J].
中国物理C, 2008, 32 (Suppl 1) : 244 –246.
ZHAO Minghua, LIN Guoqiang, ZHONG Shaopeng, et al. Design and commissioning of a 150 MeV linac for SSRF[J]. Chinese Physics C, 2008, 32 (Suppl 1) : 244 –246. (  0) 0)
|
| [2] |
汪宝亮, 赵明华, 侯汨, 等. 上海光源次谐波聚束器的优化设计及测试[J].
强激光与粒子束, 2008, 20 (6) : 1053 –1056.
WANG Baoliang, ZHAO Minghua, HOU Mi, et al. Optimization and test of sub-harmonic buncher for Shanghai Synchrotron Radiation Facility[J]. High Power Laser and Particle Beams, 2008, 20 (6) : 1053 –1056. (  0) 0)
|
| [3] |
后接. 上海光源储存环闭轨校正与轨道慢反馈研究[D]. 上海:中国科学院上海应用物理究所, 2008.
HOU Jie. Study of closed orbit correction and slow orbit feedback for the SSRF storage ring[D]. Shanghai:Shanghai Institute of Applied Physics, Chinese Academy of Sciences, 2008 (  0) 0)
|
| [4] |
张俊强, 殷重先, 高永强, 等. FPGA实现次谐波聚束器的幅相控制[J].
核技术, 2012, 35 (7) : 499 –502.
ZHANG Junqiang, YIN Chongxian, GAO Yongqiang, et al. An FPGA-based amplitude and phase control of sub-harmonic buncher[J]. Nuclear Techniques, 2012, 35 (7) : 499 –502. (  0) 0)
|
| [5] |
李林. 软X射线自由电子激光LLRF控制系统建模及算法研究[D]. 上海:中国科学院上海应用物理究所, 2015.
LI Lin. RF system modeling and research on algorithm of digital low level RF system of soft X-ray free electron lasers[D]. Shanghai:Shanghai Institute of Applied Physics, Chinese Academy of Sciences, 2015 (  0) 0)
|
| [6] |
Martin K, Lyudvig P, Christian S, et al. Drivers and software for MicroTCA.4[R]. Dresden, Germany, 2014. DOI:10.1109/RTC.2014.7097449
( 0) 0)
|
| [7] |
阎映炳. 上海光源束流位置测量数据采集系统研制及初步应用研究[D]. 上海:中国科学院上海应用物理究所, 2009.
YAN Yingbing. Research of SSRF BPM data acqusition system and preliminary application[D]. Shanghai:Shanghai Institute of Applied Physics, Chinese Academy of Sciences, 2009 (  0) 0)
|
| [8] |
Thomas S. Vector sum control of pulsed accelerating fields in lorentz force detuned superconducting cavities[D]. Hamburg:DESY, 1998
( 0) 0)
|
| [9] |
Farkas Z D, Hogg H A, Loew G A. SLED:a method of doubling slac's energy[R]. SLAC-PUB-1453, 1974
( 0) 0)
|
| [10] |
Rong L Y, Yao Y, Xu X N, et al. The improvements of LLRF control system for CSNS LINAC[R]. Lawrence Berkeley National Laboratory, 2013
( 0) 0)
|
| [11] |
原通文. 基于嵌入式系统的电子直线加速器自动频率跟踪系统[D]. 北京:北京机械工业自动化研究所, 2002.
YUAN Tongwen. An AFC system of LINAC based on embeded-system[D]. Beijing:Beijing Research Institute of Automation for Machinery Industry, 2002 (  0) 0)
|
| [12] |
范咏峰, 李平. 浅析PID参数整定[J].
中国仪器仪表, 2002 (3) : 24 –28.
FAN Yongfeng, LI Ping. PID controller tuning[J]. China Instrumentation, 2002 (3) : 24 –28. DOI: 10.3969/j.issn.1005-2852.2002.03.008 (  0) 0)
|


