放疗是癌症治疗的一个重要手段,而医用电子直线加速器作为放疗设备中最重要的核心部件,它的性能直接决定了治疗效果。被加速器加速后的电子打靶产生X射线照射深层癌细胞,或者直接引出电子来照射浅表癌细胞。通常希望最大程度地杀死某一区域内的癌细胞,同时能够最大限度地使其周围的健康细胞免受X射线或电子线的伤害。基于这种需求,需要优化医用电子直线加速器的束流品质,以提高患者的生活品质。束斑大小作为束流品质的一个重要参数,它的大小直接影响束流打靶产生剂量的X辐射分布曲线(Profile)的半影区,从而使得对束斑大小的精确定义与优化显得非常重要。
目前工业用辐照加速器由于要对束流进行扫描成平面束,所以此类加速器对束斑大小也没有要求。而在大型加速器科学装置上,束斑大小是加速管优化的一个重要指标。在束斑计算方面,这些类型的加速器侧重于把所有传输电子进行考察的均方根(Root Mean Square,RMS)束斑大小,这也是大部分加速器物理计算软件如ASTRA等直接给出的结果。在进行束流动力学计算时,直接以软件给出的束斑大小作为优化的指标非常方便,但这种单一的操作方法往往忽略了束斑大小的很多含义,无法区分束团为高斯分布与非高斯分布的差别。在此文中,针对不同的束斑计算方法进行归纳总结,明确其特有的物理含义,以便使束斑的物理本质能够在不同的场合得到正确的理解。
目前进行束斑尺寸测量的方法众多,主要有三种:一种是转化为光斑的光学思路[1-5];第二种是通过扫描丝的办法获取束流横向截面[6];第三种办法是使用束流位置检测器[7]。第一种方法,设备简单易实现,对于6-18MeV能级的低能和中高能加速管的测试精度足够高,所以联影的6MeV医用电子直线加速器采用了这种方法,把束斑转化成光斑,通过电荷耦合元件(Charge Coupled Device, CCD)相机获得光斑信息,把光斑的灰度曲线使用高斯函数进行拟合,即可得到束斑大小。基于这种思想,搭建了测试平台和束测装置,给出了测试结果,并与理论计算进行比较。
1 加速器中的束斑计算方法在加速器物理中,基于高斯分布的束斑多种计算方法都能得到一致的束斑大小。但对于非高斯分布的束团并不能完全按照高斯分布的处理思路来进行计算。因此对医用电子直线加速器来说,对非高斯分布的束团进行准确计算与测量就显得很重要。
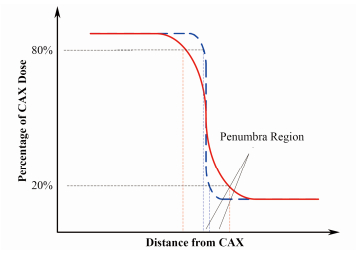
图 1给出了不同的束斑大小对剂量半影区的影响示意图,其中CAX (Central Axis)为等中心,而半影区定义为等中心剂量的20%−80%所对应的长度。图 1中虚线所代表的束斑大小要比实线所代表的束斑小,而小的束斑在打靶使用水箱进行扫描时得到的半影区也小。在动态治疗过程中,治疗头相对肿瘤位置会有一个运动,如果半影区小,意味着治疗头从肿瘤区域移开的时候,X射线可以瞬间被医用直线加速器上的初级准直器和多叶准直器(Multi-leaf Collimator, MLC)屏蔽掉,而不至于使X射线对肿瘤附近的健康细胞造成损害,从而有效减少放疗的副作用。
|
图 1 不同束斑所对应的X辐射分布曲线(profile)和相应的半影区 Fig. 1 The penumbra profiles of different spot sizes. |
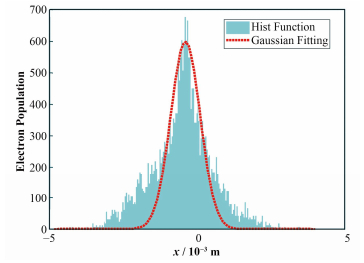
在联影6 MeV医用电子直线加速器设计过程中,使用ASTRA等束流动力学计算软件得到的束团横向分布如图 2中阴影区域所示。由于得到的束斑并不是理想的高斯分布曲线,因此使用高斯曲线(如图 2中虚线所示)进行拟合的偏离较大。基于这种非高斯分布的束斑,我们归纳了两种计算束斑的方法,适用于不同的情形。
|
图 2 束流动力学计算得到的束团分布与高斯拟合结果 Fig. 2 The electron distribution obtained by beam dynamic calculation and the Gaussian fitting result. |
均方根束斑大小的计算方法是依照其定义而来的,即把全部的传输电子(透过输出窗的电子)的横向位置参数代入式(1):
| $ {\sigma _{\operatorname{RMS} ,x}} = \sqrt {{{\bar x}^2}} ,\;{\sigma _{\operatorname{RMS} ,y}} = \sqrt {{{\bar y}^2}} $ | (1) |
式中:σRMS为束斑大小;x和y为电子横向坐标。通过式(1)计算的束斑即为ASTRA软件里直接给出的“RMS Beam Size”值。
这种方法的意义是很显然的:把100%的电子数作为统计的基点而得到束斑大小,包含了所有粒子的信息,在束流动力学优化方面比较有优势。
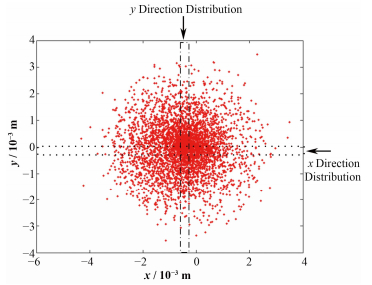
1.2 由面密度分布计算束斑在束流动力学计算软件里得到不同阶段的电子分布,为了得到束斑大小,需要对这些电子分布进行处理计算,其常用方法是画出电子分布曲线。在对电子分布进行统计的一般做法是:通过电子分布的中心画两条相互垂直的细小区域,统计这两个区域内的电子分布即为x和y方向(横向上)的面密度分布,如图 3所示。
|
图 3 电子的横向分布与x、y方向密度分布计算方法 Fig. 3 Electron distribution and the method to calculate the density distribution. |
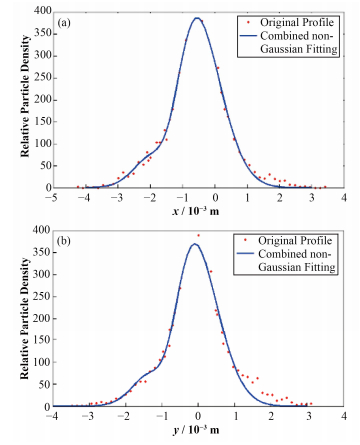
图 4给出了电子在横向的密度分布曲线,其中图 4(a)为x方向上的密度分布,图 4(b)为y方向上的密度分布。对于高斯分布,半高宽(Full width at half maximum, FWHM)与方差σ存在如下关系[8]:
| $ {\text{FWHM}} \cong 2.35\sigma $ | (2) |
|
图 4 x方向(a)与y方向(b)上的电子面密度分布及相应非高斯曲线拟合 Fig. 4 Electron area density in x direction (a) and y direction (b) combined with the non-Gaussian fitting curve. |
而对于非高斯分布,不能再使用此公式计算FWHM值来得到束斑尺寸。可以看出,电子的横向面密度分布曲线分布显然不是高斯分布,推荐的做法是直接取拟合曲线的FWHM值。图 4为理论计算的电子面密度分布曲线,直接读取拟合曲线得到x方向的FWHM=1.82 mm,y方向的FWHM=1.86mm。
1.3 两种方法的讨论对于高斯分布,使用上述两种方法得到的束斑大小是一致的,但是对于非高斯分布会有不一致的结论。
使用以上两种方法处理ASTRA计算的同一数据源得到的束斑数据,RMS法x、y分别为1.90mm、1.92mm,FWHM法x、y 分别为1.82mm、1.86mm。通过RMS方法得到的束斑大小单纯用来优化指标,是一种比较合适的方法,也是目前比较通用的一种做法。对于非高斯分布的情形,使用面密度分布来求束斑大小更具实际意义,目前各医用加速器生产商给出的也都是束斑的半高宽值。
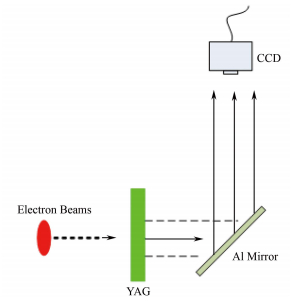
2 6 MeV加速器束斑测量实验 2.1 束斑测量装置与实验结果在工业用加速器上,为方便进行束斑测量,一般思路是将束斑转化为光斑,通过获取光斑参数得到束斑大小。由于整个束斑测量装置较为简单,在小型加速器上尤其方便,束团打在氧化钇铝晶体(Yttrium Aluminum Garnet,YAG)屏上会产生光子,在YAG屏后添加一片镜片把光反射到CCD相机里,通过CCD相机监测到的光斑即对应束流束斑。CCD相机为高像素的NI公司专业相机,以保证测量的精度。测量装置示意图如图 5所示,位于加速管末端的实验装置如图 6所示。
|
图 5 束斑测量装置示意图 Fig. 5 Illustration of the spot size measurement assembly. |

|
图 6 联影6 MeV加速器的束斑测量装置 Fig. 6 Spot size measurement assembly of the 6-MeV medical linear accelerator in UIH. |
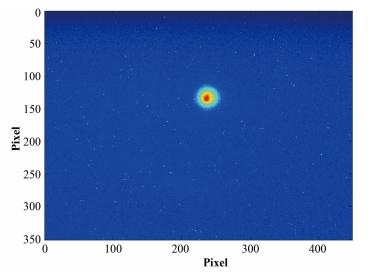
使用CCD相机得到的束斑图像如图 7所示,其中横纵坐标均为像素点。为了能得到束斑大小,还需要处理一下束斑图像。在本文§1论述了计算束斑大小的两种方法,而实验数据也将用这两种方法来处理,以便与理论结果进行比较。
|
图 7 使用CCD相机得到的束斑图像 Fig. 7 Spot image achieved by CCD camera. |
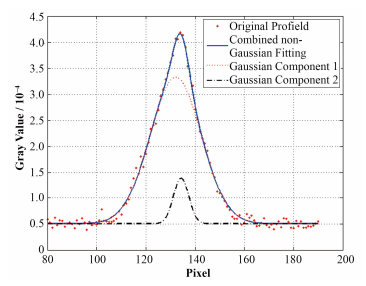
为了得到更精确的束斑大小,按照Chen等[9]提出来的思路,使用两个高斯分布来拟合,如图 8中实线所示,其与原始束斑拟合得比较好,所以其FWHM值更为恰当。
|
图 8 在x方向上使用两个高斯分布叠加成一个非高斯分布来拟合束斑 Fig. 8 The spot in x direction fitted by a combined non-Gaussian curve, which summed by two different Gaussian distributions. |
在本次实验中,对相机进行校准,得到相机的448个像素点对应长度为37.6 mm,从图 8中的拟合曲线上可以直接读出FWHM所对应的像素点为22,从而可以计算得到6 MeV医用电子直线加速器在x方向上的束斑大小为1.85 mm。同样的方法得到y方向的束斑大小为1.88 mm。最后总结理论与实验的束斑大小如表 1。
| 表 1 两种方法的理论计算值与实验值比 Table 1 A comparison between calculation results and experimental results with different methods. |
需要注意的是,由于测量装置以及人为操作过程中会引入系统误差,所以得到的束斑大小往往要比实际值偏大,在下面将对这些系统误差进行消除,以得到更为准确的束斑大小。
2.2 实验误差分析在实验过程中会不可避免地引入不同类型的系统误差,包括由于衍射效应引起的系统误差、测量平台子系统安装误差等。
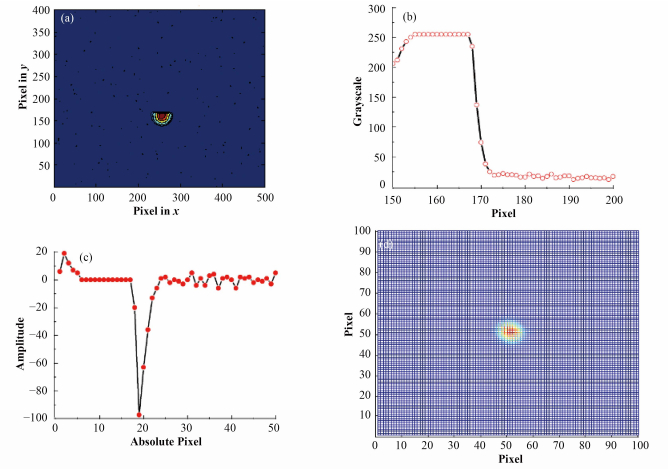
2.2.1 消除衍射效应引起的系统误差衍射效应是光学成像系统误差的主要来源,本次用来测量束斑的YAG屏厚度为0.5 mm,这个厚度不可避免地会引入系统误差。消除这种衍射效应引起的系统误差的办法是[10]:1) 使用较厚的铝板遮住半个YAG屏,此时得到一个半光斑,如图 9所示,其中图 9(b)为半光斑的y方向上的灰度曲线;2) 对这个半光斑灰度曲线进行微分,得到如图 9(c)所示的信号曲线。从图 9(c)所示的曲线可以计算得到其σ值,使用这个σ来生成标准的三维高斯分布,如图 9(d)所示。这个图 9(d)即为点扩散函数;3) 再利用点扩散函数使用反卷积算法进行图像的复原。
|
图 9 使用半光斑生成点扩散函数过程 Fig. 9 Process of generating point spread function with the half spot. |
通过这种点扩散函数,可以得到处理后的FWHM与原来图像的差值为0.01 mm,这里的0.01mm即为衍射效应所引起的系统误差。
2.2.2 测量平台各子系统安装误差测量平台上的各个子系统如YAG屏、反光镜等会引入由于安装误差引起测量结果的系统误差,针对这些误差进行误差分析是很有必要的。在表 2中将给出这些误差分析结果。
| 表 2 测量平台各子系统引入的系统误差 Table 2 The systematic errors caused by subsystem. |
表 2中θ1、θ2、θ3分别为YAG屏法向与束流的角度、反光镜与束流的角度、反光镜自身角度,而S为束斑大小。由于在实验过程中YAG屏是贴在输出窗上,θ1值为0.3°,由它引入的系统误差可近似认为是0。综合几项误差,由子系统引起的误差为±0.03 mm。
3 结语本文归纳了计算束斑大小的两种方法,这两种方法可以应用于不同的场合,其主要区别在于对象的不同而导致方法不同。RMS计算方法适用于高斯分布与非高斯分布的电子束,其绝对值具有较好的优化意义。通过画电子束的面密度分布来得到束斑大小的方法,通常需要把一定区域内的电子数用区域面积来进行归一化才能得到较准确的束斑大小。
本文搭建了束斑测量装置用来测量6 MeV的医用电子直线加速器的束斑大小。针对非高斯分布的束斑结构,使用两个高斯叠加的方式来拟合束斑,比单纯一个高斯拟合得到的结果精度要高得多。本次实验中得到考虑系统误差的束斑大小为(1.85/1.88±0.03) mm (FWHM)。
致谢 感谢刘艳芳、Maltz J、贺守波、潘刚和汪鹏等的讨论与建议。| [1] |
Jung R, Ferioli G, Hutchins S. Single pass optical profile monitoring[C]. Mainz, Germany:Proceeding of DIPAC 2003, 2003:10-14
( 0) 0)
|
| [2] |
杨国君, 张卓, 陈思富, 等. 渡越辐射在强流电子束诊断中的应用[J].
高能物理与核物理, 2005, 29 (3) : 305 –311.
YANG Guojun, ZHANG Zhuo, CHEN Sifu, et al. Research of transition radiation on intense electron beam diagnostics[J]. High Energy Physics and Nuclear Physics, 2005, 29 (3) : 305 –311. (  0) 0)
|
| [3] |
Graves W S, Johnson E D, O'Shea P G. A high resolution electron beam profile monitor[C]. Vancouver:Proceeding of the 1997 Particle Accelerator Conference, 1997:1993-1995. DOI:10.1109/PAC.1997.751084
( 0) 0)
|
| [4] |
Peter T, Tsumoru S. Measurement of small electron beam spots[J].
Annual Review of Nuclear and Particle Science, 1999, 49 : 125 –162.
DOI: 10.1146/annurev.nucl.49.1.125 ( 0) 0)
|
| [5] |
Kube G, Behrens C, Gerth C, et al. Inorganic scintillators for particle beam profile diagnostics of high brilliant and high energetic electron beams[C]. New Orleans:Proceeding of the 2012 International Particle Accelerator Conference, 2012
( 0) 0)
|
| [6] |
Blair G A, Kamps T, Lewin H, et al. R&D towards a laser based beam size monitor for the future linear collider[C]. Paris:Proceeding of EPAC 2002, 2002:1912-1914
( 0) 0)
|
| [7] |
Russell S J, Carlsten B E. Measuring emittance using beam position monitors[C]. Washington, DC:Proceeding of the 1993 Particle Accelerator Conference, 1993:2537-2539. DOI:10.1109/PAC.1993.309381
( 0) 0)
|
| [8] |
Floettamann K. DESY:ASTRA manual[OL]. 2000-9-18. http://tesla.desy.de/new_pages/TDR_CD/PartII/chapter09/references/inj_astr.pdf
( 0) 0)
|
| [9] |
Chen Q, Chen Y, Chen M L, et al. A slit method to determine the focal spot size and shape of Tomo therapy system[J].
Medical Physics, 2011, 38 (6) : 2841 –2849.
DOI: 10.1118/1.3589133 ( 0) 0)
|
| [10] |
王理. BEPCⅡ同步光在线束流测量系统研制[D]. 北京:中国科学院高能物理研究所, 2013
WANG Li. The research of on-line beam measurement system by synchrotron radiation for BEPCⅡ storage ring[D]. Beijing:Institute of High Energy Physics, Chinese Academy of Sciences, 2013 (  0) 0)
|


