2. 上海市低温超导高频腔技术重点实验室 上海 201800;
3. 中国科学院大学 北京 100049
2. Shanghai Key Laboratory of Cryogenics & Superconducting Radio Frequency Technology, Shanghai 201800, China;
3. University of Chinese Academy of Sciences, Beijing 100049, China
随着加速器技术的发展,出现了一大批高加速梯度、高平均流强和低束流发射度的加速器设计方案,其中一部分方案已经完成模型机验证。例如,美国康奈尔大学设计的基于能量回收直线加速器的5 GeV X射线同步辐射光源[1]。类似的还有日本KEK的紧凑型能量回收直线加速器cERL (compact Energy Recovery Linac)[2]、加拿大TRIUMF实验室的ARIEL 50 MeV电子直线加速器[3]以及德国HZB的能量回收直线加速器模型机bERLinpro (berlin Energy Recovery Linac prototype)[4]。这些加速器存在一个共同的特点:高平均流强下连续波模式运行。这就意味着,需要为每个加速腔提供很高的微波功率。例如,康奈尔大学的1.3 GHz连续波能量回收直线加速器,其平均流强设计值为100 mA,其注入器上每个2-cell超导腔所需的功率达到100 kW[5]。
由于陶瓷窗发热、弧放电和多电子倍增效应等原因的限制,目前已有的1.3 GHz的连续波(Continuous wave,CW)耦合器[6-9]的CW模式下测试最大传输功率均未达到75 kW。因此,使用单耦合器难以满足高功率馈入的要求。此外,单输入耦合器的使用将导致腔体的非对称,在中心轴线附近将产生明显的横向作用力。横向作用力对束团头尾作用的大小不同,从而引起束团发射度增加。
鉴于以上原因,康奈尔大学、KEK实验室以及HZB实验室在其各自的能量回收直线加速器注入器内均使用了装有双耦合器的2-cell超导腔[10-11],TRIUMF实验室则是在ARIEL的主直线加速器中所有9-cell腔上使用了双耦合器[12]。
本实验设计的1.5 GHz 5-cellSHERL超导腔[13]设计工作加速梯度为15-20 MV·m-1。未来如果被用于发展10 mA或者更高流强的连续波注入器,必须使用双耦合器提供能量。为此,完成了双耦合器功率传输的理论计算和实验验证,为安装和使用提供指导。
本文将介绍1.5 GHz同轴输入耦合器和裂缝电桥功分器的仿真优化结果。从加速腔双端口功率馈入出发,计算耦合度和输入功率的差异对反射功率的影响,并以1.5 GHz铜腔为对象进行实验验证。同时,阐述双输入耦合器横向作用力的计算并比较与单耦合器情况之间存在的差异。
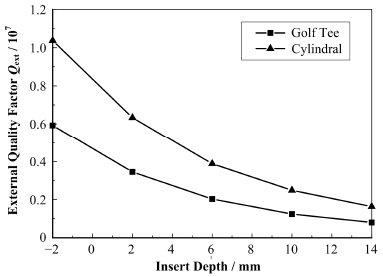
1 输入耦合器及功分器的仿真模拟为保证耦合度的可调,选择同轴型输入耦合器方案。考虑最大电场和功率承载能力的折中,同轴线特性阻抗为50 Ω。内导体半径选择为13 mm。基于增大耦合度、减小耦合器对束流的影响的目的,内导体顶部被扩大并将形状优化为椭圆形的“高尔夫球座”,其中椭圆的长短半轴长分别为20 mm和16mm。模拟结果如图 1所示,顶部优化以后,相同插入深度下,其耦合度是通常柱形顶端耦合度的两倍。这就意味着,使用新的顶部方案,可以使得内导体插入深度减小,从而减弱束团和耦合器之间的相互作用。
|
图 1 不同内导体顶部形状时的外部品质因子比较 Fig. 1 Comparisonof the external quality factors of input couplers with different tip shapes. |
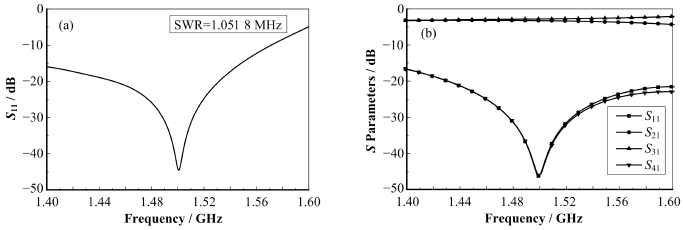
耦合器采用了比较常见的TRISTAN型陶瓷 窗[14],双窗的使用保证了单个陶瓷窗损坏时的系统真空的维持。由于矩形波导和同轴线转换器与热窗之间的场并不是纯透射电子显微镜(Transmissionelectron microscope,TEM)场,分立仿真时边界条件与真实情况不一定相符,所以将其合并一同进行仿真。改变Doorknob的参数并对WR650波导切削处理,实现微波从波导中TE10模向同轴传输线中TEM模的转换。所有部分优化达到要求之后,对整体利用时域求解器进行仿真,得到如图 2(a)所示的S11曲线。最小回波损耗小于-40 dB,驻波比(Standing Wave Ratio,SWR)小于1.05的频带宽度为18 MHz。
|
图 2 采用TRISTAN型陶瓷窗的1.5 GHz耦合器S11曲线(a)和裂缝电桥功分器S曲线(b) Fig. 2 S11 curve of the 1.5-GHz input couplerwith two TRISTAN type windows (a) and S parameters of the 1.5-GHzshort slot hybrid junction splitter (b). |
在进行功率传输时,选择使用裂缝电桥功分器[15]以保证两支输入耦合器入射功率大小相同。故此,对所需的1.5 GHz裂缝电桥功分器进行电磁仿真。为抑制其中的高次模,在优化的过程中缩短耦合区域的长度。同时,在耦合区侧壁中心处,添加一枚调谐螺钉,用于调整因加工和安装误差造成的频率和功率分配差异。结果如图 2(b)显示,频率1.48-1.52 GHz内对应的输入端口回波损耗小于-30dB,且两输出端口传输信号为-3 dB。
2 双输入耦合器功率传输优势通过单耦合器情况下入射场、反射场和传输场的计算,利用矢量叠加的原理可以得到加速腔使用双耦合器进行功率传输时各端口的反射功率。当两路微波相位相同,并且腔体处于谐振状态时,两端的反射功率表达式分别为:
| ${P_{{\rm{r}}1}} = \frac{{{{\left[{\left( {1 - {\beta _1} + {\beta _2}} \right)\sqrt {{P_{{\rm{f}}1}}} - 2\sqrt {{\beta _1}{\beta _2}{P_{{\rm{f}}2}}} } \right]}^2}}}{{{{\left( {1 + {\beta _1} + {\beta _2}} \right)}^2}}}$ | (1) |
| ${P_{{\rm{r2}}}} = \frac{{{{\left[{\left( {1 - {\beta _1} + {\beta _2}} \right)\sqrt {{P_{{\rm{f2}}}}} - 2\sqrt {{\beta _1}{\beta _2}{P_{{\rm{f1}}}}} } \right]}^2}}}{{{{\left( {1 + {\beta _1} + {\beta _2}} \right)}^2}}}$ | (2) |
式中:β1和β2分别为两端口的耦合度;Pf1、Pf2、Pr1和Pr2则分别表示加速腔两端口的入射功率和反射功率。此时,如果两端输入功率相同,每个端口的等效耦合度分别表示为:
| $\beta _1^*{\rm{ = }}\frac{{{\beta _1} + \sqrt {{\beta _1}{\beta _2}} }}{{1 + {\beta _2} - \sqrt {{\beta _1}{\beta _2}} }}$ | (3) |
| $\beta _2^*{\rm{ = }}\frac{{{\beta _2} + \sqrt {{\beta _1}{\beta _2}} }}{{1 + {\beta _1} - \sqrt {{\beta _1}{\beta _2}} }}$ | (4) |
进一步处理不难发现,当两个端口均为过耦合状态时,如果两端口耦合度之比小于0.16,弱耦合端的等效耦合度小于1,即在此端口测量得到的状态为欠耦合。
当存在束流负载时,两个输入耦合器为欠耦合状态。两端口完全对称时,端口#1的反射系数表达式为:
| ${\Gamma _1}{\rm{ = }}\frac{{{{\left( {1 + {\beta _2} - {\beta _1} - \sqrt {2{\beta _1}{\beta _2}} } \right)}^2}}}{{\left( {1 + {\beta _1} + {\beta _2}} \right)}}{\rm{ = }}{\left( {\frac{{1 - 2\beta }}{{1 + 2\beta }}} \right)^2}$ | (5) |
式中:两端口的耦合度β1和β2均等于β。从式(5)看出,两支耦合器的耦合度均为0.5时,反射系数为0。此时,每支耦合器的耦合度以及传输的功率只需要等于单耦合器情况的一半就可以为腔体提供相同的功率。这意味着,使用双耦合器,可以有效降低对耦合器性能的要求。另一方面,耦合度的减半,意味着插入深度的减小,耦合器对粒子的影响也能相应地减小。
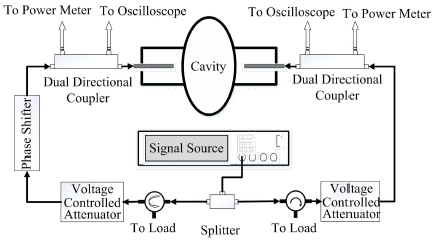
3 铜腔上实验验证为研究两支输入耦合器之间的耦合度差异对功率传输的影响,设计了一套实验装置,用于1.5 GHz铜腔的测量。如图 3所示,脉冲宽度为10 μs、周期为26 μs的方波调制信号自信号源经过功分器,分为两路,每一路均接有电压控制衰减器,用于调节入射功率。激励信号通过feedthrough从腔体两端馈入,传输线长度差异造成的相位差通过移相器来补偿。利用双向定向耦合器,分别拾取入射信号和反射信号。两路入射信号被接入功率计,实时监测,以保证两路信号大小相同。反射信号则是首先被低噪声放大器将信号增强32 dB,再经由晶体检波器,转化为直流信号,最后接入示波器中。在晶体检波器前还接入了6 dB衰减器,防止信号功率过大对其造成损坏。
|
图 3 实验装置示意图 Fig. 3 A diagram of the measurements set-up. |
当腔体处于谐振状态时,脉冲信号在脉冲前沿和后沿均会存在一个峰,脉冲前沿峰值正比于入射功率Pf,脉冲后沿峰值正比于Pe。可以通过测量两个峰值大小,利用式(6)计算耦合度:
| $\beta = \frac{1}{{2\sqrt {\frac{{{P_{\rm{f}}}}}{{{P_{\rm{e}}}}}} - 1}}$ | (6) |
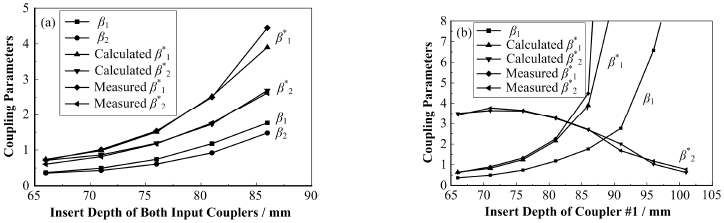
使用单输入耦合器时,测量了不同深度下对应的耦合度,并以此计算双输入情况下每个端口的等效耦合度的理论值。如图 4(a)所示,理论计算值和测量值之间相符,随着插入深度的增加,两端耦合度的增大,等效耦合度也表现出增大的趋势,并且等效耦合度大于单输入情况下的耦合度。不难看出,耦合度差异不大时,双耦合器的使用可以增大每个耦合器的耦合度。特别对于两端均为欠耦合情况,每个端口的等效耦合度均约为单输入情况下耦合度的两倍。耦合度较大时,理论计算值和测量值出现较明显的差异,这来源于测量的系统误差。
|
图 4 插入深度增加,两支耦合器耦合度同时增大时,等效耦合度的理论计算值和实际测量值的比较(a);一端插入深度保持不变,另外一端耦合度逐渐增大时,等效耦合度的理论计算值和实际测量值的变化趋势(b) Fig. 4 Comparison of theoretical value and measured value ofcoupling parameters as both input coupler were inserted simultaneously (a);Comparison of theoretical value and measured value of coupling parameters whileinsert depth of one input coupler was increased and the other was maintained (b). |
当两个耦合器之间差异较大时,则会出现另一种现象。保持端口#2的耦合度为1.45,改变端口#1的耦合度。如图 4(b)所示,随着端口#1插入深度的增加,其等效耦合度增大,而端口#2则表现出先增大后减小的趋势。理论计算和测量均表明,该转折点对应着端口#1的等效耦合度为1。随着端口#1的耦合度进一步增大,端口#2由过耦合转变为欠耦合。出现这样的现象,主要是由于端口#1反射信号与从端口#2的传输信号相反,信号的叠加导致欠耦合端前沿峰值不变,后沿峰值增大,表现出耦合度增大的趋势。但是随着耦合度的进一步增大,传输信号增加,但是反射信号减小,最终端口#2的后沿反射峰会出现极大值,即存在耦合度的极大值。进一步增大端口#1的耦合度,反射信号依然保持减小的趋势,传输信号则是先增大后减小,端口#2的反射曲线后沿峰值进一步减小,甚至由过耦合状态过渡为欠耦合状态。
4 横向作用力计算单耦合器会造成场的非对称性,导致横向作用力的存在。对于低能量的束团而言,横向作用力的存在将引起发射度的增加。对于单耦合器情况,腔体内部横向作用力主要来源是耦合器引起的非对称场。所以,使用双输入耦合器可以大幅度减小横向作用力对束流发射度的影响。
横向作用力的作用大小可以用横向和纵向动量变化的比值来表示:
| ${K_{x,y}} = \frac{{\Delta {P_{x,y}}}}{{\Delta {P_z}}} = \frac{{{V_{x,y}}}}{{{V_z}}}$ | (7) |
式中:Vx、Vy和Vz分别为横向、纵向电压,表达式为:
| $\left( {\begin{array}{*{20}{c}} V\\ {{V_y}}\\ {{V_z}} \end{array}} \right) = \frac{1}{c}\int {\left( {\begin{array}{*{20}{c}} {{E_x} - c{B_y}}\\ {{E_y} - c{B_x}}\\ {{E_z}} \end{array}} \right)} {{\rm{e}}^{j\omega z/c}}{\rm{d}}z$ | (8) |
由于束流通过腔体时,耦合器附近的场应该为行波场,但是CST本征模求解器无法做到模拟束流通过腔体时的场分布求解。通过在耦合器端口分别设置电边界和磁边界,在本征模求解器中求出两种情况的下的本征模,利用模拟的结果叠加在输入耦合器处构造入射波和反射波,从而得到与实际运行时相符的场分布[16]。
对于连续波运行,反射仅仅来源于腔体的失谐。在调谐系统的控制下,δω/ω很小,反射波对横向作用力的贡献可以忽略。因此,本文只考虑无反射情况下纯入射波引起的横向作用力。
模拟结果如图 5显示,单支耦合器会造成场分布的非对称性,使得中心轴线上的Ey和Bx不为零。在耦合器位置,电场引起的横向力的方向快速变化,而磁场引起的横向力则在此位置存在一个明显的单峰。横向作用力主要由磁场引起,并且集中在y方向,大小为:
| ${K_y} = \left( {0.99 - 5.21i} \right) \times {10^{ - 4}}$ | (9) |
横向作用力分为两个部分,实部作用于整个束团,造成束团的偏转;虚部主要作用于束团头部,进而驱动束团尾部振荡,引起发射度的增加[17]。
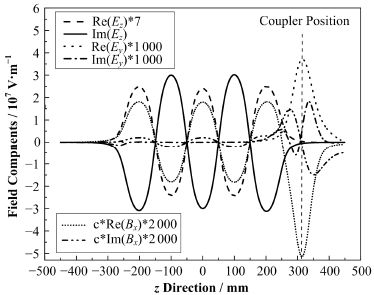
|
图 5 使用单耦合器时腔体内中心轴线上场分布,z方向为电子加速方向,y方向为耦合管中心轴线方向 Fig. 5 Field distribution on axis for single input couplersituation,z stands for direction where beams fly,y stands forthe axis of coupler pipe. |
实际情况下,由于插入深度无法保证完全相同,双耦合器无法做到绝对对称,横向作用力也不可能完全消除。插入深度相差为1 mm,相对耦合度差异大于10%。此时,中心轴线上TM010模的场的横向电场、磁场的分量仍然存在,但与单耦合器相比减弱了很多。计算得到y方向横向作用力大小为:
| ${K_{y1}} = \left( {5.07 - 7.72i} \right) \times {10^{ - 5}}$ | (10) |
所以使用对称的双耦合器,即使插入深度不同,仍然能大幅度减小横向作用力。不过,考虑到横向作用力不能完全消除,输入耦合器还需要放置在束流轨迹的下游,保证束流通过耦合器附近时能量足够高。
5 结语本文对使用双耦合器的加速腔功率传输进行了计算分析,给出了微波入射功率相同情况下,两端等效耦合度的表达式。铜腔上的验证实验结果与理论计算吻合,结果显示,两端均为欠耦合时,双输入对每个端口耦合度起到增强的作用;但当两者均为过耦合且耦合度存在差异时,耦合度小的一端的等效耦合度则会随着另一端耦合度的增加逐渐减小,甚至在两端比值小于0.16时出现欠耦合的情况。
使用双耦合器进行功率馈入,能将单支耦合器传输的功率减半,降低了对耦合器性能的要求。同时,耦合度的减半,意味着更小的插入深度,可以降低束流与耦合器的相互作用。此外,模拟显示使用双耦合器,即使在不能保证完全对称的情况下,也能有效减小由输入耦合器引起的横向作用力,减缓束流发射度的增加。所以,双输入耦合器是目前发展高平均流强、低束流发射度加速器的唯一必然选择。
| [1] |
Hoffstaetter G H, Bazarov I V, Sagan D, et al. A lattice for a 5 GeV ERL in the CESR tunnel[C]. Proceedings of the 2003 Particle Accelerator Conference, Portland, Oregon, 2003. DOI:10.1109/PAC.2003. 1289498
( 0) 0)
|
| [2] |
Nakamura N. Review of ERL projects at KEK and around the world[C]. Proceedings of 3rd International Conference on Particle Accelerator, New Orleans, USA, 2012
( 0) 0)
|
| [3] |
Koscielniak S, Ames F, Baartman R, et al. ARIEL and the TRIUMF e-linac initiative, a½-MW electron linac for rare isotope beam production[C]. Proceedings of the 14th Conference on Linear accelerator, Victoria, Canada, 2008
( 0) 0)
|
| [4] |
Abo-Bakr M, Anders W, Burrill A, et al. Status of the HZB ERL project bERLinpro[C]. Proceedings of the 5th International Particle Accelerator Conference, Dresden, Germany, 2014
( 0) 0)
|
| [5] |
Shemelin V, Belomestnykh S, Geng R L, et al. Dipole-mode-free and kick-free 2-cell cavity for the SC ERL injector[C]. Proceedings of the 2003 Particle Accelerator Conference, Portland, Oregon, 2008. DOI:10.1109/PAC.2003.1288777
( 0) 0)
|
| [6] |
Veshcherevich V, Belomestnykh S, Quigley P, et al. High power test of first input couplers for Cornell ERL injector cavities[C]. Proceedings of PAC 2007, Albuquerque, 2007. DOI:10.1109/PAC.2007.4441248
( 0) 0)
|
| [7] |
Knobloch J, Anders W, Martin M, et al. CW operation of the TTF-Ⅲ input coupler[C]. Proceedings of 2005 Particle Accelerator Conference, Knoxville, Tennessee, 2003. DOI:10.1109/PAC.2005.1591445
( 0) 0)
|
| [8] |
Kako E, Noguchi S, Shishido T, et al. High power tests of CW input couplers for cERL injector cryomodule[C]. Proceedings of 3rd International Conference on Particle Accelerator, New Orleans, USA, 2012
( 0) 0)
|
| [9] |
Mitra A K, Ang Z, Calic S, et al. High power coupler test for TRIUMF e-linac SC cavities[C]. Proceedings of LINAC2012, Tel-Aviv, Israel, 2012
( 0) 0)
|
| [10] |
Watanabe K, Noguchi S, Kako E, et al. Development of the superconducting RF 2-cell cavity for the cERL injector at KEK[J].
Nuclear Instruments and Methods in Physics Research Section A, 2013, 714 : 67 –82.
DOI: 10.1016/j.nima.2013.02.035 ( 0) 0)
|
| [11] |
Neumann A, Abo-Bakr M, Anders W, et al. Booster cavity and fundamental power coupler design issues for bERLinPro[C]. Proceedings of IPAC2014, Dresden, Germany, 2014
( 0) 0)
|
| [12] |
Zvyagintsev V, Beard C D, Grassellino A, et al. Nine-cell elliptical cavity development at TRIUMF[C]. Proceedings of SRF 2011, Chiacago, USA, 2011
( 0) 0)
|
| [13] |
杨峻, 马震宇, 王岩, 等. 1500 MHz 5-cell超导腔的仿真优化[J].
核技术, 2015, 38 (6) : 060103 .
YANG Jun, MA Zhenyu, WANG Yan, et al. Simulation of a 1500 MHz 5-cell superconducting cavity[J]. Nuclear Techniques, 2015, 38 (6) : 060103 . DOI: 10.11889/j.0253-3219.2015.hjs.38.060103 (  0) 0)
|
| [14] |
Akemoto M, Yamazaki Y. High power input coupler for the TRISTAN APS cavity[C]. The 7th Symposium on Accelerator Science and Technology, Osaka, Japan, 1989
( 0) 0)
|
| [15] |
Riblet H J. The short-slot hybrid junction[C]. Proceedings of the Ire, 1952, 40(2):180-184. DOI:10.1109/JRPROC. 1952.274021
( 0) 0)
|
| [16] |
Gulliford C, Bazarov I, Belomestnykh S, et al. Asymmetric focusing study from twin input power couplers using realistic RF cavity field maps[J].
Physical Review Special Topics Accelerators and Beams, 2011, 14 : 032002 .
DOI: 10.1103/PhysRevSTAB.14.032002 ( 0) 0)
|
| [17] |
Juntong N, Beard C, Burt G, et al. RF coupler kicks and wake-fields in SC accelerating cavities[C]. Proceedings of EPAC 2008, Genoa, Italy, 2008
( 0) 0)
|


