2. 中国科学院大学 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
国家大科学工程上海光源(Shanghai Synchrotron Radiation Facility,SSRF)是第三代同步辐射光源。而第三代光源最显著特征就是大量引入插入件,尤其是真空内波荡器,能够工作在很小的间隙下,可以获得更强的磁场,与真空外插入件相比,可以获得更好品质的同步辐射光,所以在第三代同步辐射光源中有非常广泛的应用[1]。目前研制真空内插入件,垫补磁场参数是在没有真空腔体的情况下进行的,当垫补完成后,磁阵列需要被整体拆下安装到真空腔体内。由于腔体内的空间非常有限,目前常用的基于大理石平台的磁测系统由于无法在安装真空腔体后对插入件磁场参数进行测量,所以真空插入件磁场性能好坏受机械拆装的重复性影响非常大。为了能够测量到真空腔体内磁阵列的磁场参数,我们设想把一根直线导轨安装到真空腔体内,霍尔探头安装到直线导轨的滑块上,这样滑块做往返带动霍尔探头一起运动就可以测量到插入件的磁场分布了。
一般,真空插入件的长度在1.6 m左右,测量用的直线导轨需要在2.4 m左右(为覆盖两端的漏场)。根据已有的经验,这么长的导轨安装到真空腔体后会有比较大的变形,导轨变形量级在±150μm左右。这样的变形对磁场测量结果有非常大的影响,折算到光学相位误差,可达到2°-3°,这将影响我们对波荡器磁场参数的判断,因此,准确测量导轨的变形量并且根据变形量对磁场加以矫正是非常有必要的。本课题研究的主要目标就是为了解决真空插入件在安装了真空腔体后磁场的精确测量问题,一套基于PSD (Position Sensitive Detector)的位置测量系统被用于测量直线导轨的形变数据。本文将对实验系统的搭建和实验结果进行详细的描述。
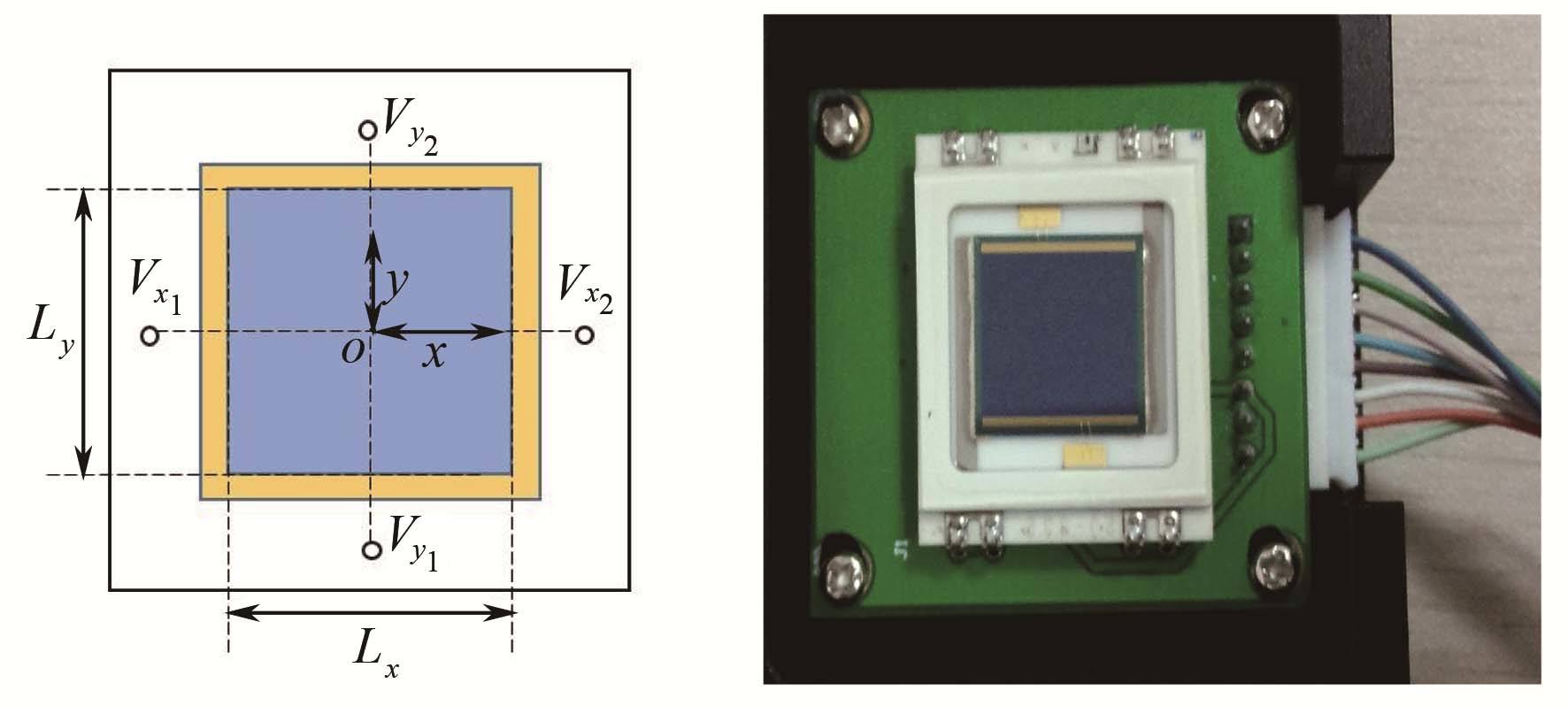
1 测量原理 1.1 二维PSD工作原理PSD的工作原理是基于横向光电效应。PSD光敏面是半导体材料,当一束光射到PSD光敏面(图1)上时,会产生电子空穴对。在耗尽层内电场作用下载流子会发生定向移动,空穴进入P层,电子进入N层,从而在PSD表面会产生光电流。由PSD等效电路图可知,这种电流信号大小与表面P层电阻呈反比,又因为P层电阻是均匀的,因此电阻大小和光斑位置是线性关系,于是电流信号大小和光斑位置也呈反比并且是线性变化的[2]。
|
图1 二维PSD光敏面 Fig.1 Two-dimension PSD sensitivity surface. |
一般来讲电流信号会经放大电路转换为电压信号再进行计算,因此只要测得入射点在PSD光敏面边缘的电压V1和V2,就能得到光斑位置。当坐标原点选取PSD中心位置时,横纵坐标表示为[2, 3]:
| $$x = {{{L_x}} \over 2}{{{V_{{x_2}}} - {V_{{x_1}}}} \over {{V_{{x_2}}} + {V_{{x_1}}}}},y = {{{L_y}} \over 2}{{{V_{{y_2}}} - {V_{{y_1}}}} \over {{V_{{y_2}}} + {V_{{y_1}}}}}$$ | (1) |
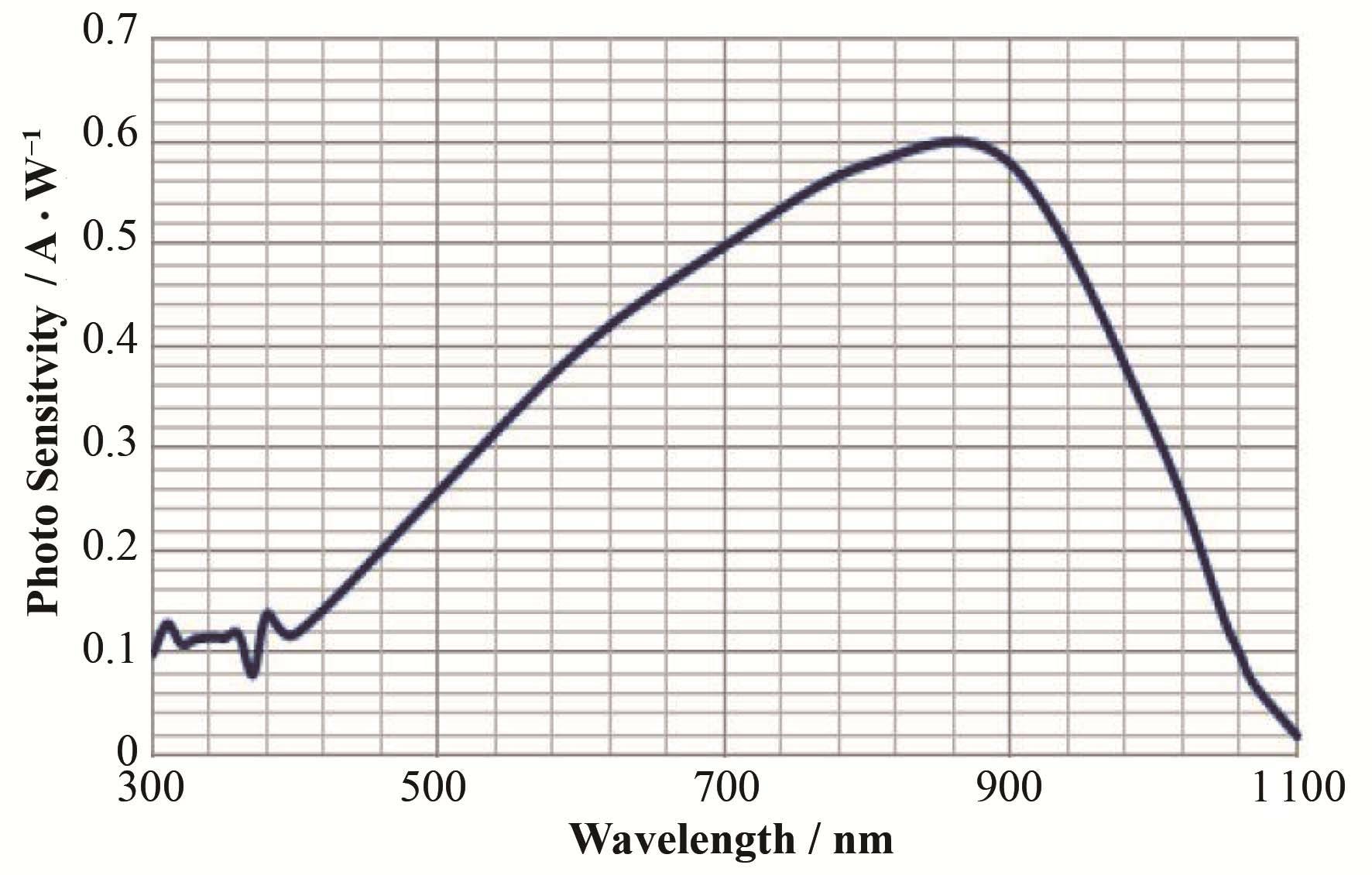
PSD对不同波长的光敏感性也不同,随着波长(300 nm以上)的增加敏感性先增大后减小,如图2所示,峰值出现在900 nm附近,但由于900 nm已经进入不可见光范围,对于光学系统的准直调整不利,因此我们选取波长630 nm、功率1 mW的光源以便于准直和调整。同时,我们还在PSD表面加装了一片600-700 nm带通滤波片,尽可能减弱背景光的干扰。
|
图2 PSD光敏性参数曲线 Fig.2 PSD photosensitive parametric curves. |
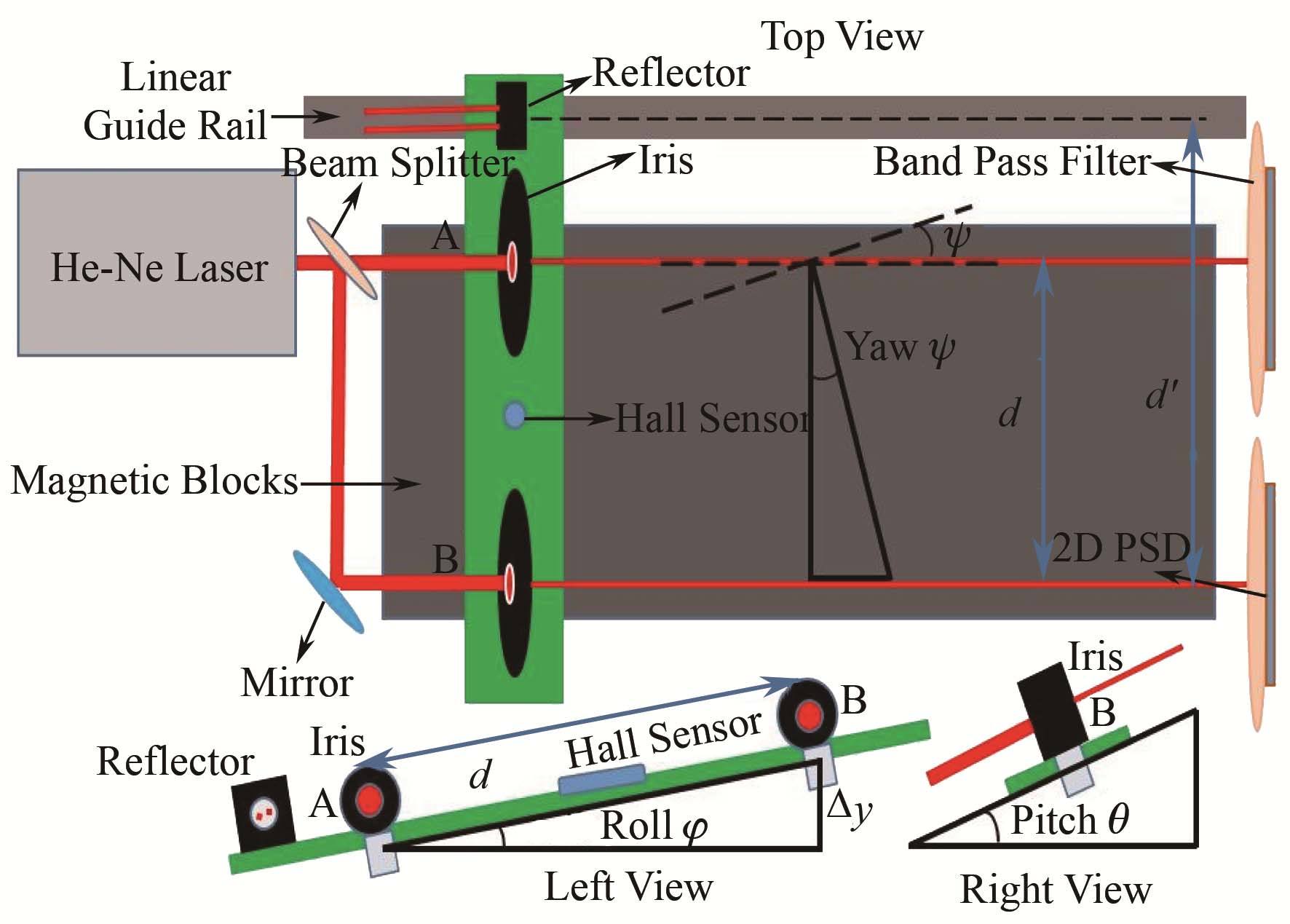
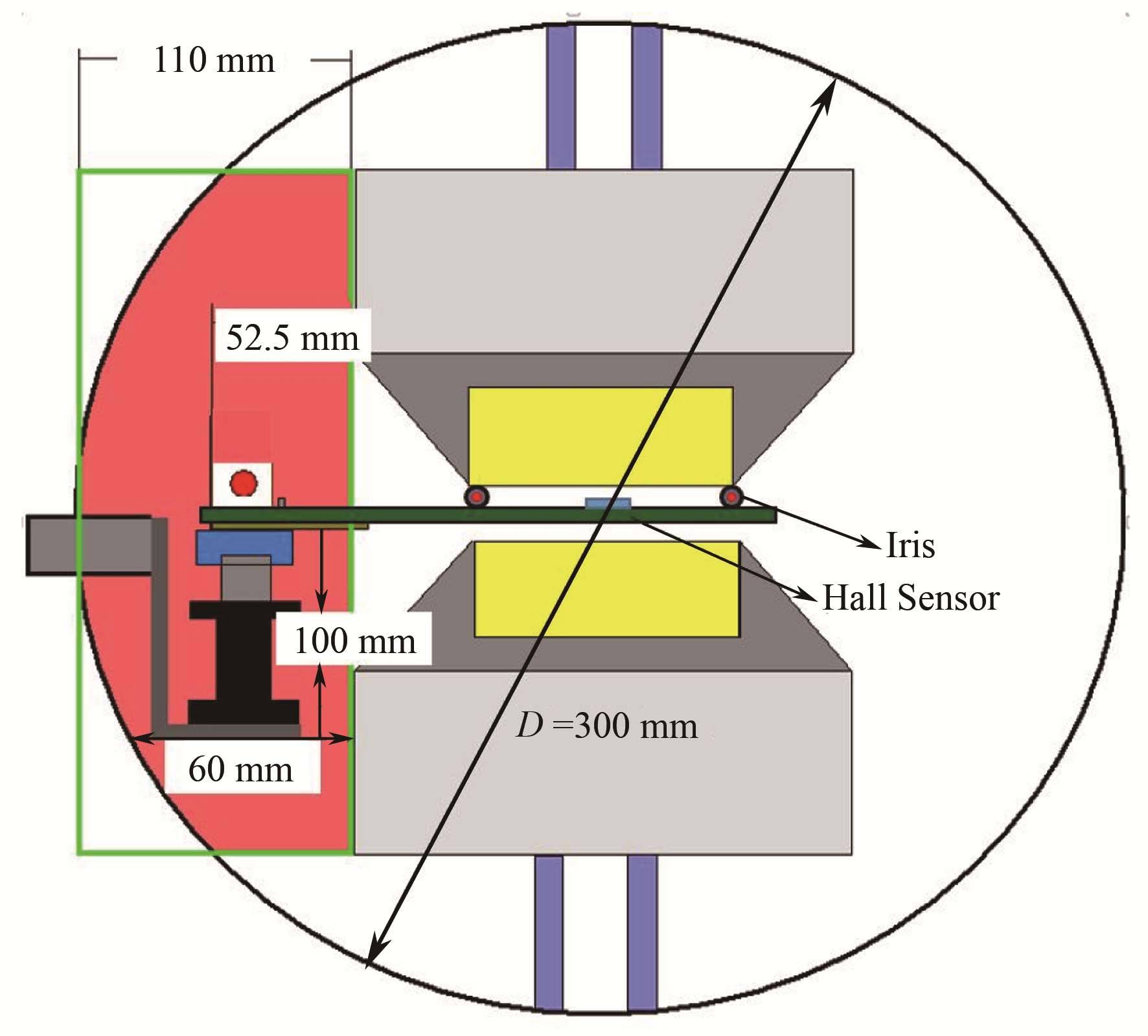
在实际应用于波荡器磁测时需要两片PSD才可以实现导轨的直线度和霍尔探头三个欧拉角度pitch(θ)、yaw(ψ)和roll(φ)的测量。在图3所示的PSD位置测量系统原理三视图中,A和B分别代表两个光阑(iris),它是一种通过改变孔径大小来调节光束强弱的光学器件。光阑在沿导轨行进过程中产生的横向位移与导轨形变是一致的,只要入射光斑半径足够大,透过光阑照射到PSD光敏面上的光斑位移变化就能反应出导轨形变。连接导轨的霍尔探头支撑系统和光阑在波荡器真空腔内的空间位置如图4所示,真空腔体的直径是300 mm,导轨安装位置在波荡器极面上处于中心悬空。
选取光阑中心和反射镜几何中心水平面作为参考平面,光阑B和反射镜中心距离d'作为霍尔探头的臂长,两个光阑A和B的中心距离固定为d,霍尔传感器置于两个光阑之间的中心位置。使用同一台He-Ne激光器,通过1:1的分光镜将光束分成两束,PSD和光阑的空间位置关系如图3所示。这样通过测得A和B两点位置坐标就可以计算得到霍尔传感器的横向位置偏离Δx、Δy和滚转角φ:
$$\Delta x = {{{x_{\rm{A}}} + {x_{\rm{B}}}} \over 2},\matrix{
{} & {} \cr
} \Delta y = {{{y_{\rm{A}}} + {y_{\rm{B}}}} \over 2}$$
(2)
$$\sin \varphi = {{{y_{\rm{B}}} - {y_{\rm{A}}}} \over d}$$
(3)
|
图3 应用于波荡器磁测的PSD位置测量系统的原理 Fig.3 Principle of PSD system in undulator magnetic field measurement. |
|
图4 霍尔探头和光阑在波荡器的空间位置 Fig.4 Location of Hall Sensor and iris in undulator. |
理论上我们可以对导轨x和y方向的直线度数据进行多项式拟合得到拟合函数Fx(z)和Fy(z),对于导轨上任意一点zn,霍尔探头的俯仰角θ和偏航角ψ可通过对相应的函数求导计算获得:
| $$\tan \theta = {F'_y}{\rm{(}}{z_n}{\rm{)}}$$ | (4) |
| $$\tan \psi = {F'_x}{\rm{(}}{z_n}{\rm{)}}$$ | (5) |
假设霍尔传感器与纵向位置反射镜之间的垂直距离和水平距离是ly和lx,那么俯仰角θ和偏航角ψ导致霍尔传感器在纵向位置上偏离Δz:
| $$\Delta z = {l_y}\sin \theta + {l_x}\sin \psi $$ | (6) |
Δz将破坏霍尔传感器在纵向位置测量点的等距性,Δx和Δy使得霍尔传感器的相对横向位置发生偏离,θ、ψ和φ导致霍尔传感器与被测磁场的正交性发生变化,根据相关插入件磁场理论和霍尔传感器磁测原理可知,这些位置偏差和角度偏差使得磁测结果发生误差。
对于垂直方向y来说,磁场测量值与理想位置的值之间的关系为:
| $${B_{ym}}{\rm{ = }}{B_{yo}}({z_n})\cosh \left( {{{2{\rm{\pi }}a} \over {{\lambda _{{\rm{ID}}}}}}\Delta y({z_n})} \right)$$ | (7) |
式中:λID代表波荡器磁场周期长度;a是由磁场周期长度、材料和gap决定的系数。
对于纵向位置z来说,磁场测量值和理想位置的值之间的关系式为:
| $${B_{zm}}{\rm{ = }}{B_{zo}}({z_n} + \Delta z)$$ | (8) |
根据这些关系校正磁测结果的误差,否则将影响到我们对真空插入件真实磁场参数的判断,从而进一步影响对磁场参数的垫补和优化。
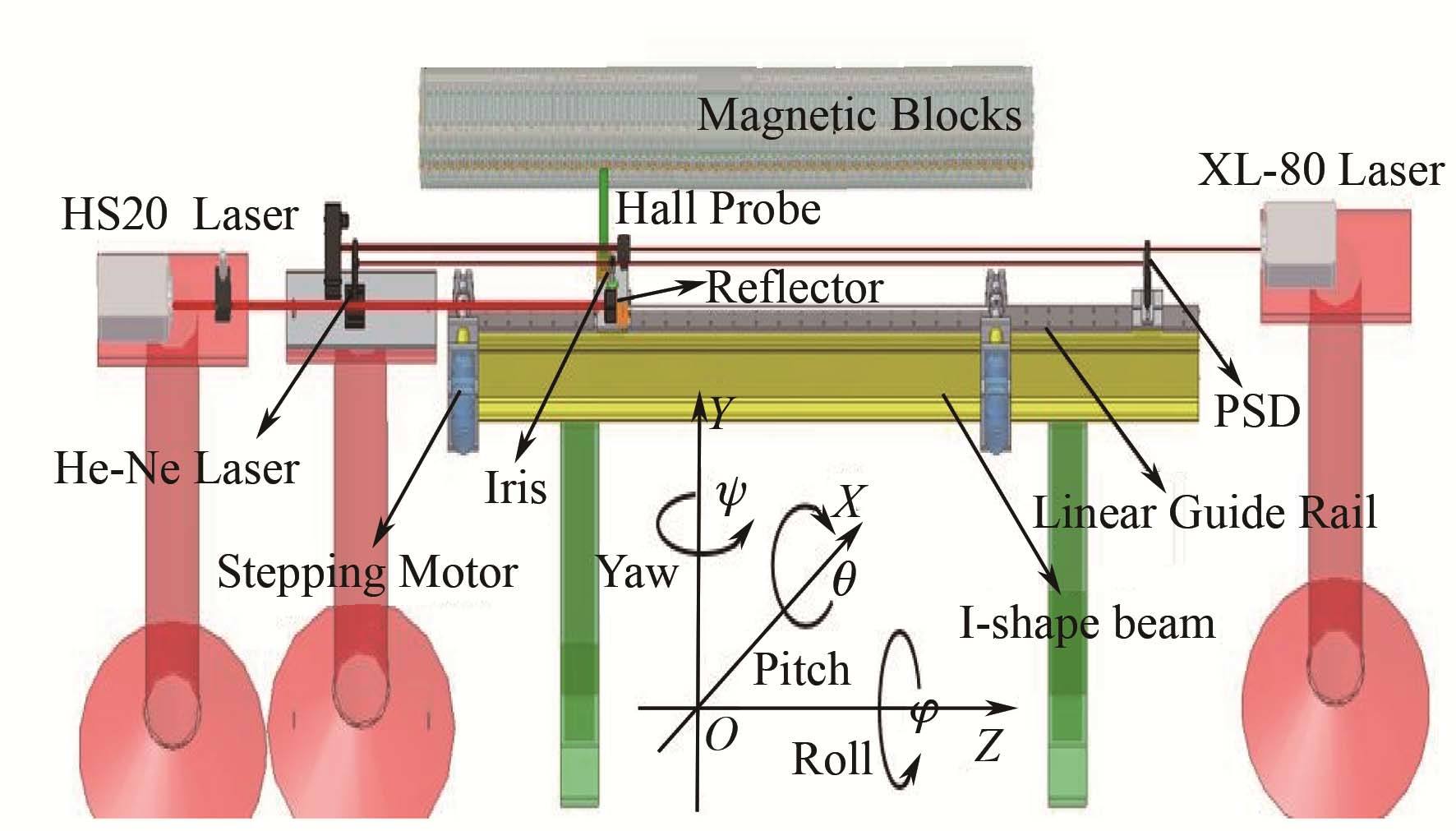
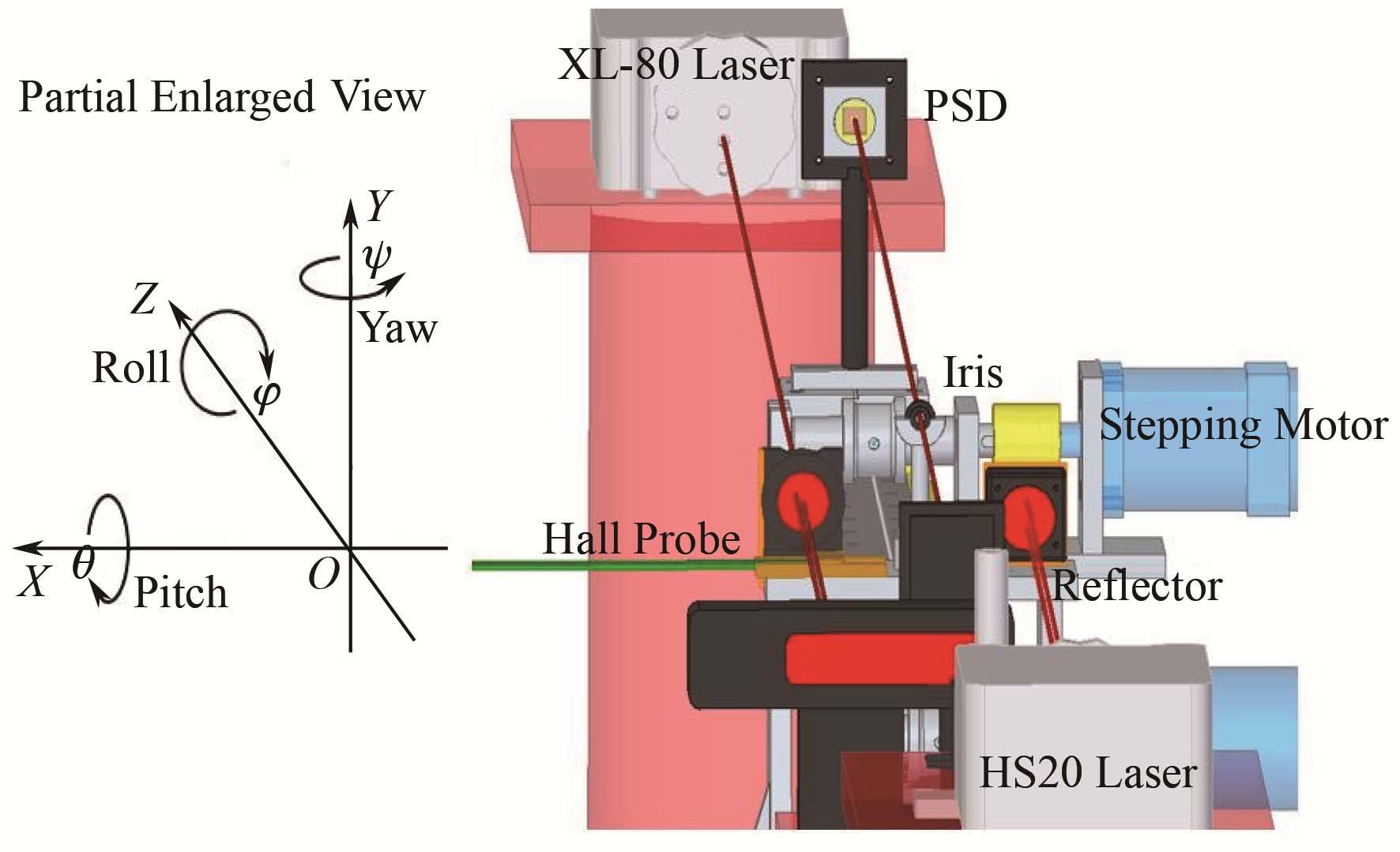
1.3 PSD位置测量系统构成我们先选取一片PSD搭建PSD位置测量系统以近似获得霍尔传感器横向位置坐标。PSD位置测量系统由PSD (10 mm×10 mm)、光阑(孔径调节范围0.5-6.8 mm)、He-Ne激光器、数据采集系统、运动控制系统构成。系统整体结构设计如图5所示,系统局部放大如图6所示。光阑和霍尔探头固定放置在同一滑块,PSD放置在另一滑块,He-Ne激光器放置在PSD相对的一侧,光斑位置穿过光阑入射到PSD光敏面。He-Ne激光器、光阑和PSD光敏面中心位置通过调节使其保证在同一直线上,原因是PSD在距离器件中心2/3、光敏面总面积的75%范围内线性度较好,从而保证测量范围较大[4]。PSD探测器输出的4路信号由4台Keithley2701数字电压表同时采集,采样方式为外部触发模式,触发信号来自用于测量霍尔探头纵向位置HS20激光器的差分输出信号,因此该系统可实现On-flying测量。On-flying测量是能基于光栅尺位置的连续测量,中间不停顿并且测量的步长可编程,我们采用LabVIEW编写了应用程序接口和人机界面。
|
图5 PSD位置测量系统结构设计 Fig.5 Structural design of PSD position measuring system. |
|
图6 PSD位置测量系统局部放大 Fig.6 Partial enlarged view of PSD position measuring system. |
根据系统结构设计的布局,在工字梁上逐个安装系统部件。实验进行之前,先对光斑中心位置进行初始化校准,实际测量位置是根据式(1)求得的坐标减去零点偏置。PSD位置测量系统搭建完成后如图7所示。

|
图7 PSD位置测量系统 Fig.7 PSD position measuring system. |
随着导轨两端的步进电机转动,载有光阑和霍尔探头的滑块从直线导轨的一端平稳移动到另一端。雷尼绍(Renishaw)XL-80激光光斑直径为6 mm,调节光阑孔径在2 mm左右,这样使得该系统有±2mm的直线度测量范围。整个过程中光阑随着导轨的形变而发生位置变化,穿过光阑孔径的光斑横向位置相应改变,PSD光敏面测量到的光斑变化也就测量出了导轨的形变。
PSD放大电路的4路电压信号被4台Keithley电压表同步采集,LabVIEW编写的数据采集程序将测量数据输出到表格中,通过计算就可以转换为直线导轨的横向直线度数据。我们利用MATLAB编程作图可得x和y方向沿导轨(z方向)的大致变化,进行分段拟合可得到变化曲线,拟合的目的主要是尽可能减弱随机噪声信号对测量结果的影响。
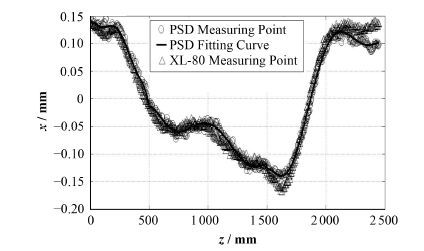
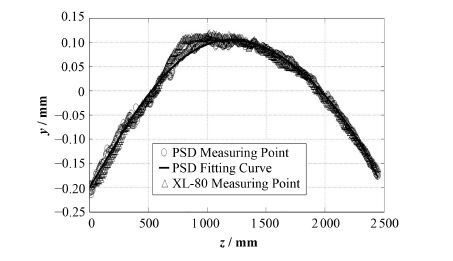
图8是x方向变化曲线,图9是y方向变化曲线。图8和图9的横坐标表示沿z方向的位移,导轨总长度是2500 mm。z方向每隔0.5 mm等距触发采样,坐标点沿z方向是均匀分布。由图8可见,直线导轨在1500 mm处形变最大,达到0.20 mm。拟合曲线有多处拐点,说明导轨横向位置x沿z方向有多处扭曲。由图9显示,y方向的直线度最大值达到0.15 mm。拟合曲线最大拐点有一处,说明导轨在y方向有一小段凸起。结合两图采样点坐标轴上的数值,可得到采样点的测量精度达到微米级,y方向最大的临近点跳变约为10 μm。实验过程中我们还发现背景光的干扰和直线导轨的微小振动对测量结果有一定影响。
|
图8 导轨横向位置x的变化曲线 Fig.8 Curves of lateral position x along the guide rail. |
|
图9 导轨横向位置y的变化曲线 Fig.9 Curves of lateral position y along the guide rail. |
这些直线度测量数据将被用于校正霍尔探头的磁场测量数据。我们同时还用XL-80激光干涉仪系统对导轨x和y方向的直线度做了测量,测量结果与PSD位置测量系统的结果基本吻合。为获得空间有限的腔体内的插入件磁场参数,在狭小或封闭空间内进行磁场测量,我们搭建了PSD位置测量系统。相对于XL-80激光干涉仪系统,该系统的光阑尺寸比光学反射镜镜头尺寸小,光阑孔径便于调整和快速安装;PSD有分辨率高,响应速度快等优点。
3 结语本实验成功搭建了国内首套基于真空内波荡器磁场测量的PSD位置测量系统,该系统实现了On-flying测量,能快速准确地测量霍尔探头横向位置坐标,实验结果显示,该系统定位精度在5 μm左右,基本满足磁场校正的精度要求。未来如想进一步提高测量精度,需要选择功率和稳定性更高的激光器(PSD位置测量用),滤波效果更好的带通滤波片尽可能减弱背景光对测量结果的影响,对PSD的4路输出电压信号进行低通滤波以减弱电信号噪声。
| 1 | 刘祖平. 同步辐射光源物理引论[M]. 合肥:中国科学技术大学出版社, 2009:216-240 LIU Zuping. Physics instruction of synchrotron radiation facility[M]. Hefei:University of Science and Technology of China Press, 2009:216-240( 1) 1) |
| 2 | 裴先登, 罗春, 黄浩. PSD高精度测量系统的研究与设计[J]. 华中科技大学学报(自然科学版), 2004, 32(2):7-9. DOI:10.3321/j.issn:1671-4512.2004.02.003 PEI Xiandeng, LUO Chun, HUANG Hao. Research of high precision position measurement system and its design based on PSD[J]. Journal Huazhong University of Science & Technology(Nature Science Edition), 2004, 32(2):7-9. DOI:10.3321/j.issn:1671-4512.2004.02.003( 2) 2) |
| 3 | Blank S, Shen Y T, Xi N, et al. High precision PSD guided robot localization:design, mapping, and position control[C]. Proceedings of the 2007 IEEE/RSJ International Conference on Intelligent Robots and Systems San Diego, CA, USA, 2007:52-57. DOI:10.1109/IROS.2007.4399621( 1) 1) |
| 4 | 施隆照, 杨琦. 高精度二维四边形结构PSD信号调理电路设计[J]. 福州大学学报(自然科学), 2008, 36(2):215-216. DOI:10.3969/j.issn.1000-2243.2008.02.012 SHI Longzhao, YANG Qi. A design of signal processing circuit for high precision two dimensional tetra-lateral PSD[J]. Journal of Fuzhou University(Nature Science), 2008, 36(2):215-216. DOI:10.3969/j.issn.1000-2243. 2008.02.012( 1) 1) |


