2. 中国科学技术大学 核科学技术学院 合肥 230026
2. School of Nuclear Science and Technology, University of Science and Technology of China, Hefei 230026, China
过冷沸腾是指被加热液体主体温度低于相应压力下饱和温度,而壁面过热度达到气泡产生条件时发生的沸腾,其起始点被称为ONB(Onset of nucleate boiling)。在ONB上游的区域,传热机理为液体单相对流传热;自ONB起,由于有液体汽化吸热并可能叠加气泡扰动与边界层破坏,导致通道壁面上出现新的传热机理,传热过程变得复杂,通道内的流动开始从单相流转变为两相流。可见,ONB是描述过冷沸腾形成过程的重要参数,建立更为准确的模型预测这个点的位置对于提高热工分析精度具有十分重要的意义,但经验公式无法描述ONB发生过程,近年来有学者尝试采用两相数值模拟技术来深入分析这一现象,譬如李松蔚[1]与李权等[2]利用商用计算流体动力学(Computational Fluid Dynamics,CFD)软件对环管与圆管内的过冷沸腾现象进行模拟;Eckhard等[3]利用CFX-5对不同燃料元件布置方式下的系统换热能力进行了模拟,将加热棒束上出现温度分布最高的区域预测为后期出现过冷沸腾的位置;Li等[4]运用Ansys Fluent对不同状态下的圆管和矩形管道进行过冷沸腾情况模拟,通过运用Euler model中不同子模型进行了计算,分析了各子模型的适用性。上述这些计算均关系过冷沸腾的宏观现象,其判断是否出现过冷沸腾依然是根据局部参数并结合经验关系式,与以往不同之处在于可以获得较为精确的局部参数。另一类数值计算方法从模拟气泡出发,研究加热面产生气泡的条件,譬如Lal等[5]模拟了主流过冷和接近饱和状态下气泡生长的情况,对气泡产生以及脱离过程及流场和温场有着详细的描述,但是这类计算的边界条件以及其中的辅助模型依然要强烈依赖于实验,所以并不是完全的数值解,因此数值模拟目前依然无法取代实验关系式。以往的研究通过实验或理论的方法获得了壁面热流密度q与温差T的经验公式[6, 7, 8],由于观测手段存在局限,譬如无法准确捕获极微小气泡的产生等,其结果与实验值符合得不好(实验值偏大)。本文认为,传统观念中的ONB实际上不是点而是沿流动方向的一段距离,它从液相汽化点(Onset of fluid vaporization,OFV)持续到气泡脱离气穴的点(ONB),本文在此假设基础上通过唯象方法进行分析,描述过冷沸腾发生的过程,并对比本文所建立的模型结果与实验值。
1 汽化起始点OFV的形成理论如下:
考虑液体中一个半径为r的气泡,平衡时,由亥姆霍兹关系式得气泡内外压强差为:
| ${{p}_{\operatorname{g}}}-{{p}_{l}}=\frac{2\sigma }{r}$ | (1) |
式中:pg为气泡内部压强;p1为液体压强;σ为气液界面表面张力系数。
根据克劳修斯-克拉伯龙方程,气液两相平衡时压强p与温度T的关系满足:
| $ \frac{\operatorname{d}p}{\operatorname{d}T}=\frac{h}{T({{v}_{g}}-{{v}_{l}})} $ | (2) |
式中:h为相变潜热;vg、v1分别为气液两相摩尔体积。
因vg>>v1,式(2)可简化为: $\frac{\operatorname{d}p}{\operatorname{d}T}=\frac{h}{T{{v}_{\operatorname{g}}}}$ ,由理想气体状态方程pvg=RT,代入得:
| $ \frac{\operatorname{d}p}{\operatorname{d}T}=\frac{h}{R{{T}^{2}}} $ | (3) |
式中:R为理想气体常数。
式(1)与(3)联立,积分可得气泡内外饱和温度差:
| ${{T}_{\operatorname{g}}}-{{T}_{\operatorname{l}}}=\frac{R{{T}_{\operatorname{g}}}{{T}_{\operatorname{l}}}}{h}\ln(1+\frac{2\sigma }{r{{p}_{\operatorname{l}}}})$ | (4) |
式中:Tg为气泡内饱和温度;T1为液体饱和温度。
在较为广泛的范围内可以认为 $r{{p}_{\operatorname{l}}}\approx 1$ ,所以: $\frac{2\sigma }{r{{p}_{1}}}>>1$ , $\ln(1+\frac{2\sigma }{r{{p}_{\operatorname{l}}}})\approx \frac{2\sigma }{r{{p}_{\operatorname{l}}}}$ ,式(4)可以化简为:
| ${{T}_{\operatorname{g}}}-{{T}_{\operatorname{s}}}=\frac{2\sigma {{v}_{\operatorname{g}}}{{T}_{\operatorname{s}}}}{hr}$ | (5) |
气泡形成模型如图 1所示,该模型采用以下假设:

|
图 1 FV点气泡形成模型 Fig.1 Bubble formation model of OFV. |
1)气泡形状为去头球形;
2)气泡不影响加热壁面附近温度分布;
3)当气泡顶端液体温度为气泡内部饱和温度时,气泡停止生长。
由图 1可得,气泡顶端到壁面距离y满足:
| $y=r\left(1+\cos \theta \right)$ | (6) |
式中:θ为接触角,由液体与壁面性质决定。
因y非常小,在边界层内很薄的一个区域,可认为热量仅靠热传导传递,液体热导率也可以视为常数,从而靠近壁面的温度T近似为线性分布,有:
| $T={{T}_{\operatorname{w}}}-{{q}_{\operatorname{w}}}y/{{k}_{\operatorname{l}}}$ | (7) |
式中:Tw为壁面温度;qw为壁面热流密度;k1为液体热导率。
若所求流体点气泡完成生长后的半径为r,则r应当满足气泡顶端流体温度为Tg,由式(6)与(7)可得,气泡顶端流体温度T为:
| $T={{T}_{\operatorname{w}}}-\frac{{{q}_{\operatorname{w}}}r(1+\cos \theta)}{{{k}_{\operatorname{l}}}}$ | (8) |
因T=Tg,由式(5)与(8)得:
| ${{T}_{\operatorname{w}}}-{{T}_{\operatorname{s}}}=\frac{2\sigma {{T}_{\operatorname{s}}}{{v}_{\operatorname{g}}}}{hr}+\frac{{{q}_{\operatorname{w}}}(1+\cos \theta)}{k}r$ | (9) |
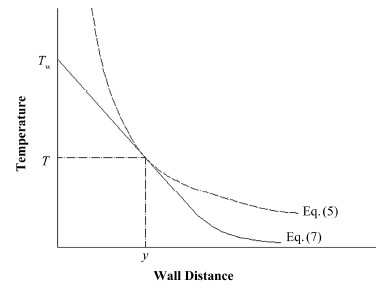
如何确定r,现有两种方法。第一种方法,如图 2所示。
|
图 2 壁面温度分布 Fig.2 Wall-temperature distribution. |
根据OFV定义,流体首先开始汽化的点为OFV点,故有气泡半径为r时,式(5)与(7)曲线恰相切,即:
| $$\frac{2\sigma {{v}_{\operatorname{g}}}{{T}_{\operatorname{s}}}}{h{{r}^{2}}(1+\cos \theta)}=\frac{{{q}_{\operatorname{w}}}}{{{k}_{\operatorname{l}}}} | (10) |
从而,
| ${{r}^{2}}=\frac{2k{{T}_{\operatorname{s}}}\sigma {{v}_{\operatorname{g}}}}{(1+\text{cos}\theta)h{{q}_{\operatorname{w}}}}$ | (11) |
将式(11)其代入式(9),最终得到:
| ${{q}_{\operatorname{w}}}=\frac{hk}{8(1+\text{cos}\theta){{T}_{\operatorname{s}}}\sigma {{v}_{\operatorname{g}}}}{{({{T}_{\operatorname{w}}}-{{T}_{\operatorname{s}}})}^{2}}$ | (12) |
此方法首先由Davis等[8]采用,用于预测ONB点,但实验发现,对于给定的壁面热流密度,壁面过热度理论值与实验值相比偏小(这是由于在实验中观察到的已经是气泡长大到一定程度时的过热度,而不是气泡刚刚开始形成时的数值)。根据本文假设,式(12)描述的实际上是OFV点,从而解释了这一现象。
2 过冷沸腾起始点本文认为,ONB点气泡脱离气穴的原因是流体拖曳力得以克服气泡与气穴间的表面张力,从而气泡应该具有足够的半径 r,应使拖曳力与表面张力成一定比例。通过量纲分析法,可获得此比例与相关参数的函数关系式。利用已有实验数据通过用反推的方法获得r值,可确定此关系公式,进而用此关系公式预测r值与热流密度,即本文提出的第二种确定r的方法。
2.1 流体拖曳力与表面张力之比的确定湍流粘性底层中:
| $u=\frac{{{\tau }_{\operatorname{w}}}}{\mu }y$ | (13) |
式中:u为流体局部速度;τw为壁面切应力;μ为动力粘度;y为与壁面的距离。
布拉修斯公式:
| ${{h}_{\operatorname{f}}}=\frac{0.316\ 4}{R{{e}^{0.25}}}\cdot \frac{l}{d}\cdot \frac{{{v}^{2}}}{2g}$ | (14) |
式中:hf为沿程压力损失;l为管道长度;Re为雷诺数;d为管道直径;v为流体平均速度;g为重力系数;ρ1为流体密度。
因 ${{\tau }_{\operatorname{w}}}=\frac{{{h}_{\operatorname{f}}}dg{{\rho }_{\operatorname{l}}}}{4l}$ ,故有 $u\propto \frac{{{\rho }_{\operatorname{l}}}{{v}^{2}}y}{R{{e}^{0.25}}\mu }$ 。
按照图 1,单位面积上受流体拖曳力 ${{f}_{1}}\propto {{\rho }_{\operatorname{l}}}{{u}^{2}}$ ,气泡受到的总拖曳力为: ${{F}_{1}}\propto \int_{\theta -\frac{\pi }{2}}^{\frac{\pi }{2}}{\pi r{}^{2}{{\cos }^{2}}\alpha \cdot {{\rho }_{\operatorname{l}}}{{u}^{2}}}\operatorname{d}\alpha \propto \frac{{{\rho }_{\operatorname{l}}}^{3}{{r}^{4}}{{v}^{4}}}{Re_{{}}^{0.5}{{\mu }^{2}}}$ 。
表面张力 ${{F}_{2}}\propto \sigma r$ ,从而 $\frac{{{F}_{1}}}{{{F}_{2}}}\propto \frac{{{\rho }_{\operatorname{l}}}^{3}{{r}^{3}}{{v}^{4}}}{\sigma R{{e}^{0.5}}{{\mu }^{2}}}$ 。
2.2 其它参数进一步推测可能与r相关的参数:水的热导率k,表面张力系数σ,饱和温度Ts,热流密度q,蒸汽比容vg,汽化潜热h,流体速度v,通道直径d,压强p,壁面过热度△T,水密度ρ1,水粘性系数μ,水热容Cp,再加上r,共计14个参数,可组成10个无量纲参数。除了已经导出的流体阻力及表面张力之比 $\frac{{{\rho }_{\operatorname{l}}}^{3}{{r}^{3}}{{v}^{4}}}{\sigma R{{e}^{0.5}}{{\mu }^{2}}}$ ,其它还有 ${{(\frac{2k\sigma {{T}_{\operatorname{s}}}{{v}_{\operatorname{g}}}}{{{q}_{\operatorname{w}}}h{{r}^{2}}(1+\cos \theta)})}^{0.5}}$ 、ρ1vg、 $\frac{\Delta T}{{{T}_{\operatorname{s}}}}$ 、 $\frac{r}{d}$ 、Re、 $\frac{pv}{q}$ 、 $\frac{qd}{k\Delta T}$ 、 $\frac{{{v}^{3}}{{\rho }_{\operatorname{l}}}}{q}$ 、Pr,其中:Pr为普朗特数。
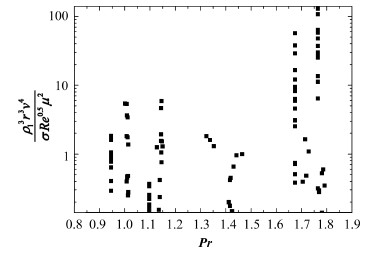
2.3 无量纲参数之间的关系在进行各个无量纲数分析之前,通过调研获得了Rohsenow[9]、Sato[6]、Sudo[10]与Ahmadi[11]实验数据。Rohsenow[9]实验条件:压强10.4-13.8MPa,流道直径4.57mm的圆形;Sato[6]实验条件:压强1.01×105Pa,流道截面为7mm×10mm的矩形;Sudo[10]实验条件:压强0.12MPa,流道截面为2.25mm×50mm的矩形;Ahmadi[11]实验条件:压强96-860Pa,流道截面为10mm×20mm的矩形。通过上文量纲分析获得的 $\frac{{{\rho }_{\operatorname{l}}}^{3}{{r}^{3}}{{v}^{4}}}{\sigma R{{e}^{0.5}}{{\mu }^{2}}}$ 、 ${{(\frac{2k\sigma {{T}_{\operatorname{s}}}{{v}_{\operatorname{g}}}}{{{q}_{\operatorname{w}}}h{{r}^{2}}(1+\cos \theta)})}^{0.5}}$ 、ρ1vg、 $\frac{\Delta T}{{{T}_{\operatorname{s}}}}$ 、 $\frac{r}{d}$ 、Re、 $\frac{pv}{q}$ 、 $\frac{qd}{k\Delta T}$ 、 $\frac{{{\rho }_{\operatorname{l}}}^{3}{{r}^{3}}{{v}^{4}}}{\sigma R{{e}^{0.5}}{{\mu }^{2}}}$ 、 $\frac{{{v}^{3}}{{\rho }_{\operatorname{l}}}}{q}$ 与Pr等无量纲参数,在大量试算的基础上,如图 3、4,发现大量无量纲参数之间并无明显规律。

|
图 3 $\frac{{{\rho }_{l}}^{3}{{r}^{3}}{{v}^{4}}}{\sigma R{{e}^{0.5}}{{\mu }^{2}}}$ 与 $\frac{pv}{q}$ 关系 Fig.3 $\frac{{{\rho }_{l}}^{3}{{r}^{3}}{{v}^{4}}}{\sigma R{{e}^{0.5}}{{\mu }^{2}}}$ variation with $\frac{pv}{q}$ . |
|
图 4 $\frac{{{\rho }_{\operatorname{l}}}^{3}{{r}^{3}}{{v}^{4}}}{\sigma R{{e}^{0.5}}{{\mu }^{2}}}$ 与Pr关系 Fig.4 $\frac{{{\rho }_{\operatorname{l}}}^{3}{{r}^{3}}{{v}^{4}}}{\sigma R{{e}^{0.5}}{{\mu }^{2}}}$ variation with Pr. |
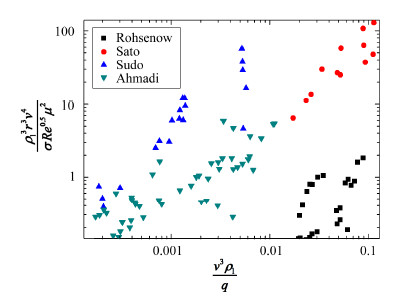
而 $\frac{{{\rho }_{l}}^{3}{{r}^{3}}{{v}^{4}}}{\sigma R{{e}^{0.5}}{{\mu }^{2}}}$ 与 $\frac{{{v}^{3}}{{\rho }_{\operatorname{l}}}}{q}$ 存在明显函数关系。
由图 5及其实验条件,可获得下列ONB点关系式:
| $\frac{{{\rho }_{l}}^{3}r{{v}^{4}}}{\sigma R{{e}^{0.5}}{{\mu }^{2}}}=300{{(\frac{{{v}^{3}}{{\rho }_{l}}}{q})}^{0.888}}$ | (15) |
|
图 5 $\frac{{{\rho }_{\operatorname{l}}}^{3}{{r}^{3}}{{v}^{4}}}{\sigma R{{e}^{0.5}}{{u}^{2}}}$ 与 $\frac{{{v}^{3}}{{\rho }_{\operatorname{l}}}}{q}$ 关系 Fig.5 $\frac{{{\rho }_{\operatorname{l}}}^{3}{{r}^{3}}{{v}^{4}}}{\sigma R{{e}^{0.5}}{{u}^{2}}}$ variation with $\frac{{{v}^{3}}{{\rho }_{\operatorname{l}}}}{q}$. |
式(15)的适用条件为:压强小于1MPa,流道为圆形或长宽比不大的矩形。
| $\frac{{{\rho }_{\operatorname{l}}}^{3}r{{v}^{4}}}{\sigma R{{e}^{0.5}}{{\mu }^{2}}}=60\ 271{{(\frac{{{v}^{3}}{{\rho }_{\operatorname{l}}}}{q})}^{1.41}}$ | (16) |
式(16)的适用条件为:压强小于1MPa,流道为长宽比较大的矩形。
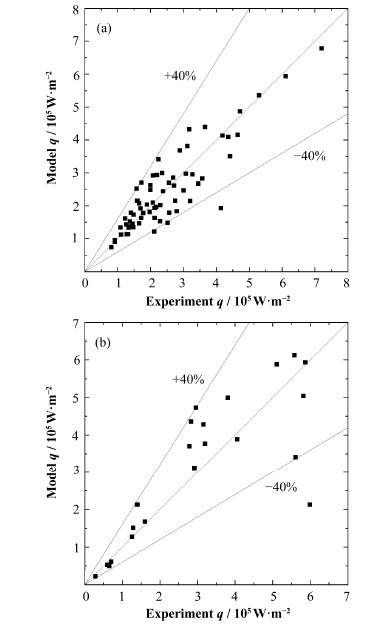
2.4 结果检验由式(15)与(16)可得气泡脱离半径r,将r代入式(9),即可得热流密度q与壁面过热度△T的关系式。式(15)所得理论值与实验值对比如图 6(a),式(16)所得理论值与实验值对比如图 6(b)。由图 6可知,拟合结果与实验值符合较好,不存在实验值均偏大的情况[6, 7, 8]。
|
图 6 式(15) (a)、式(16) (b)与实验结果比较 Fig.6 Comparison between Eq.(15) (a), Eq.(16) (b) and experimental data. |
本文在已有研究的基础上,认为过冷沸腾起始点实际上更应该视为是一个流动长度,它起于流体开始汽化点OFV,终于气泡脱离气穴点ONB,通过理论分析与量纲分析的方法,获得了新的ONB预测公式,并利用已有实验数据进行了检验,得到以下结论:
1)OFV气泡半径可通过式(11)确定,ONB气泡半径可通过式(15)、(16)确定,结合式(9),可得到壁面热流密度与过热度的关系式,其误差分布要好于实验关系式。
2)在压强为1 MPa时,OFV气泡半径量级为1mm,ONB点气泡半径是OFV点气泡半径的1.5-3倍。可以看出,OFV点与ONB点气泡大小并不存在量级上的差别,因而两者在流程上的间距很小。加之气泡大小接近光学显微镜分辨的极限,导致实验上难以观察区分[11],所以仍需要开展实验与数值分析重新对ONB进行研究。
| 1 | 李松蔚, 张虹, 姜胜耀, 等. 竖直环管内低压水过冷沸腾数值模拟研究[J]. 核动力工程, 2014, 35(1):46-51 LI Songwei, ZHANG Hong, JIANG Shengyao, et al. Numerical simulation research of subcooled boiling water in vertical concentric annulus pipe under low pressure[J]. Nuclear Power Engineering, 2014, 35(1):46-51( 1) 1) |
| 2 | 李权, 焦拥军, 于俊崇. 竖直加热圆管内过冷沸腾及CHF 数值模拟[J]. 核动力工程, 2015, 36(1):168-171. DOI:10.13832/j.jnpe.2015.01.0168 LI Quan, JIAO Yongjun, YU Junchong. Simulation of subcooled boiling and critical heat flux in uniformly heated tubes[J]. Nuclear Power Engineering, 2015, 36(1):168-171. DOI:10.13832/j.jnpe.2015.01.0168( 1) 1) |
| 3 | Eckhard K, Bostjan K, Yury E. CFD modelling of subcooled boiling-concept, validation and application to fuel assembly design[J]. Nuclear Engineering and Design, 2007, 237:716-731. DOI:10.1016/j.nucengdes. 2006.10.023( 1) 1) |
| 4 | Li H, Vasquez S A, Punekar H, et al. Prediction of boiling and critical heat flux using an eulerian multiphase boiling model[C]. ASME 2011 International Mechanical Engineering Congress and Exposition, American Society of Mechanical Engineers, 2011:463-476( 1) 1) |
| 5 | Lal S, Sato Y, Niceno B. Direct numerical simulation of bubble dynamics in subcooled and near-saturated convective nucleate boiling[J]. International Journal of Heat and Fluid Flow, 2015, 51:16-28. DOI:10.1016/j.ijheatfluidflow.2014.10.018( 1) 1) |
| 6 | Sato T, Matsumura H. On the conditions of incipient subcooled boiling with forced convection[J]. Bulletin of JSME, 1964, 7(26):392-398( 4) 4) |
| 7 | Bergles A E, Rohsenow W M. The determination of forced convection surface boiling heat transfer[J]. ASME Journal of Heat Transfer, 1964, 86(3):365-372( 2) 2) |
| 8 | Davis E J, Anderson G H. The incipience of nucliate boiling in forced convection flow[J]. AIChE Journal, 1966, 12(3):774-780( 3) 3) |
| 9 | Rohsenow W M, Clark J A. Heat transfer and pressure drop data for high heat flux densities to water at high subcritical pressures[R]. The Office of Naval Research, 1951( 2) 2) |
| 10 | Sudo Y, Miyata K, Ikawa H, et al. Experimental study of incipient nucleate boiling in narrow vertical rectangular channel simulating subchannel of upgraded JRR-3[J]. Journal of Nuclear Science and Technology, 1986, 23(1):73-82( 2) 2) |
| 11 | Ahmadi R, Ueno T, Okawa T. Bubble dynamics at boiling incipience in subcooled upward flow boiling[J]. International Journal of Heat and Mass Transfer, 2012, 55:488-497. DOI:10.1016/j.ijheatmasstransfer.2011.09.050( 3) 3) |


