燃耗计算是反应堆堆芯设计及计算分析的关键环节^[1]。随着先进反应堆技术的发展，反应堆的几何结构和中子能谱愈发复杂^{[2, 3, 4, 5]}，对燃耗计算结果的精度要求也越来越高，因此发展高精度的燃耗计算方法和程序的需求十分迫切。

燃耗计算通常是输运计算和点燃耗计算的相互耦合。蒙特卡罗燃耗计算继承了蒙特卡罗输运计算方法强大的复杂几何处理能力，可以精确计算各类系统中子通量分布及能谱，从而获得高精度的燃耗计算结果，因此成为目前的研究热点。根据耦合方法的不同，蒙特卡罗燃耗程序可以分为外耦合方式和内耦合方式^[6]，外耦合方式是通过独立接口程序耦合蒙特卡罗输运程序（如MCNP^[7]）和点燃耗程序（如ORIGEN^[8]）；而内耦合方式则是将点燃耗计算作为子功能加入输运程序中，这种方式较外耦合更为精准和高效。

常见的点燃耗计算方法大致有线性子链解析(Transmutation Trajectory Analysis,TTA)方法和矩阵指数法两类，其中矩阵指数法计算速度快，步长包容性高，是目前应用最为广泛的一类方法。这类方法中，由Pusa等^[9]提出的切比雪夫有理逼近方法(Chebyshev rational approximation method,CRAM)由于不需要单独处理短寿命核素，计算精度更高。

此外，由于燃耗计算涉及核素较多，为了在保证输运计算效率的情况下尽量降低内存开销，国内外也提出了一些能量查找方法，如Serpent的双索引方法^[10]、RMC的能量箱方法^[11]等。

超级蒙特卡罗核计算仿真软件系统SuperMC(Super Monte Carlo Simulation Program for Nuclear and Radiation Process)^{[12, 13, 14, 15]}是一款具有完全自主知识产权的通用、智能、精准的核系统设计优化与安全评价软件。SuperMC以蒙特卡罗与确定论方法耦合及先进信息技术应用为技术特色，以集成几何与物理自动建模^{[16, 17, 18]}；可视分析与虚拟仿真^[19]、云计算服务为易用性特色。目前SuperMC已通过2000多个国际基准模型与实验的校验，其中聚变堆包括国际热核聚变实验堆(International Thermonuclear Experimental Reactor,ITER)^{[20, 21]}、聚变动力堆FDS-II^[22]、快堆(International Atomic Energy Agency-BN600,IAEA-BN600)、IAEA-ADS(International Atomic Energy Agency-Accelerator Driven Systems)等反应堆综合应用验证。本文基于SuperMC，采用CRAM点燃耗算法和桶排序能量查找方法，进行了内耦合蒙特卡罗燃耗计算研究与验证工作。

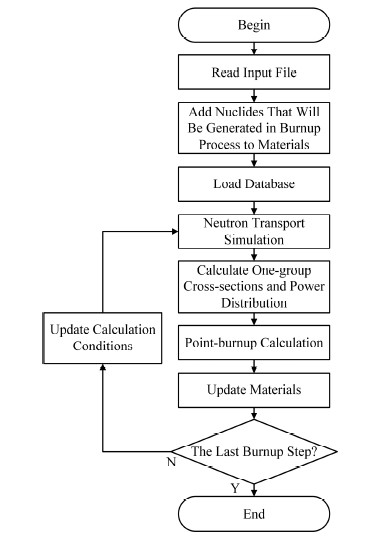
本文实现的内耦合蒙特卡罗燃耗计算流程如图 1所示，其中点燃耗计算模块采用CRAM对点燃耗方程组进行求解。在反应堆中，点燃耗方程组通常具有如下形式^[23]，对于核素i，其核素密度n_i随时间变化率为：

图 1(Fig.1)

图 1 燃耗计算流程图 Fig.1 Flow chart of burnup calculation.

式中： $\phi(t)$为中子通量密度； ${\lambda _i}$为核素i的衰变常数； ${\sigma _{i,k}}$为核素i发生k反应的微观截面； ${\sigma _{i,k}}$为核素j衰变后生成子核i的概率； ${y_{j,k,i}}$为核素j发生k反应后，生成子核i的概率。若定义矩阵元 ${A_{i,j}}$为：

则可以得到点燃耗方程组的矩阵形式及其指数解：

式中： $\vec n(t)$表示t时刻核素密度向量； ${\vec n_0}$表示向量的初始值。CRAM对式(4)做如下近似^[9]：

式中：I表示单位矩阵；a₀、a_i、θ_i均为预先求出的系数。从而将问题转化为求解k/2个稀疏线性方程的问题。

在输运计算过程开始前，需要对燃耗过程可能产生的核素预先进行添加。本方法首先读取初始材料中的核素，然后采用层序遍历的方式将其生成路径中的核素逐一加入材料中，最后进行数据库读取。

为了获得点燃耗计算所需参数，需要根据当前材料信息进行输运计算，以获取各燃耗区的中子通量密度、功率分布以及各核素单群截面。本文采用基于超精细能谱的单群截面统计方法^{[10, 24]}，首先在输运过程中统计各燃耗区的中子能谱，在输运计算结束后，对燃耗区内核素的各个反应进行单群截面计算。

在完成单群截面和功率分布计算后，根据当前燃耗步总热功率，对各燃耗区进行功率分配和源强转换。使用这些参数更新燃耗矩阵，并根据上一步核素密度和当前燃耗步长，对各燃耗区调用点燃耗计算模块，得到当前燃耗深度下的核素密度，并更新材料信息，进行下一步输运计算。

在蒙特卡罗粒子输运过程中，每产生一条径迹，都需要查找中子当前能量在材料里所有核素的能量网格中的位置。常规做法是依次对材料中每个核素的能量网格进行二分查找。当涉及核素较多时，这种搜索方法效率很低。

现有主流解决方法是统一能量网格方法^[10]，该方法将所有核素的能量网格合并为一个统一能量网格，这样仅需要对该网格进行一次查找，就可以通过映射获得当前能量在所有核素能量网格中的位置，从而提高搜索速度。但是，燃耗计算一般涉及到上百种核素，而该方法需要储存各核素能量网格与统一能量网格的映射关系，因此使用这种方法将造成大量的内存开销。

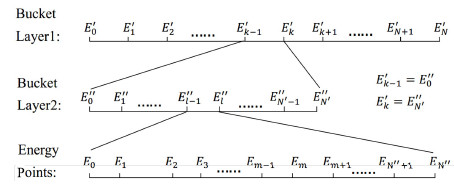
考虑到在内存中访问数组的高效性，借鉴桶排序算法以及文献[11]中能量箱划分的思想可知，对于每个核素的能量网格，若使用固定间隔将其取值范围划分为一系列如图 2中Bucket Layer1所示的顺序排布的数值区间，即“桶”，并将能量网格中的能量点按数值大小划分到相应的桶中，这样在进行能量查找时仅对相应的桶进行搜索，将大大缩小搜索范围。同时考虑到核素能量网格中能量点分布的不均匀性，可能导致某些桶中仍然存在较多能量点，因此需要使用更小的间隔，对能量点数量大于阈值的桶进行再次划分，形成如图 2所示的嵌套结构，从而可以适应不同的能量网格分布，保证各个桶中的能量点数均小于阈值。

图 2(Fig.2)

图 2 桶排序能量查找方法示意图 Fig.2 Schematic diagram of bucket sort energy searching method.

在对某一核素进行能量查找时，首先通过能量E找到该核素中包含该能量的桶，如图 2中的 $(E_{k-1}^{'},E_{k}^{'})$。若该桶中存在次级划分，则再次通过E在该划分中进行搜索，这样直到找到直接包含能量点的桶，如 $(E_{l-1}^{''},E_{l}^{''})$。最后对该桶中的能量点进行二分搜索，就可以找到E在核素能量框架中的位置，从而起到加速作用。由于该方法只需要储存各个桶的边界和容量，较统一能量网格方法可以节省大量内存。

为了验证本文实现的燃耗计算方法的正确性，选用燃料棒燃耗问题以及IAEA-ADS国际基准题^[25]进行了测试，并使用IAEA-ADS基准题测试了桶排序能量查找方法的性能。

本文以压水堆燃料棒为例，计算了富集度为3%的UO₂燃料棒经过焚烧达到30MW·d·(kgU)^-1燃耗深度，再经过3年衰变后核素密度变化情况。燃料棒的燃耗问题涵盖了燃耗计算中常用的中子反应和衰变反应，核素生成关系复杂，可以初步验证本文实现的燃耗计算方法的正确性。本文以采用微扰TTA方法的Serpent作为对比程序，计算采用ENDF/B-VII数据库提供的截面、裂变产物和衰变数据。其中部分重要核素计算结果列于表 1。从表 1可以看出，本文的计算结果和Serpent的结果基本一致，绝大部分核素偏差均在1%以内，可见在计算含有复杂反应链的问题时，本文实现的燃耗计算方法能够得到准确的结果。另外，在计算²⁴⁴Cm时偏差相对较大(1.6%)，这是由于微扰TTA方法在处理环形燃耗链时会引入微扰以避免奇点问题，从而导致较大偏差。

表 1(Table 1)

表 1 燃料棒燃耗问题计算结果Table 1 Results of fuel rod burnup problems. 核素 Nuclides Serpent / 1×1024m-3 本文 This paper / 1×1024m-3 偏差 Deviation / % 核素 Nuclides Serpent / 1×1024m-3 本文 This paper / 1×1024m-3 偏差 Deviation / % 79Se 9.4729×10-8 9.4863×10-8 0.14 138Ba 1.5319×10-5 1.5347×10-5 0.18 83Kr 7.8486×10-7 7.8506×10-7 0.03 139La 1.4326×10-5 1.4351×10-5 0.18 90Sr 1.0399×10-5 1.0417×10-5 0.17 142Ce 1.3061×10-5 1.3086×10-5 0.19 94Zr 1.3845×10-5 1.3870×10-5 0.18 153Eu 9.4473×10-7 9.3602×10-7 -0.92 95Mo 1.3804×10-5 1.3828×10-5 0.17 234U 8.3821×10-9 8.3925×10-9 0.12 99Tc 1.3360×10-5 1.3381×10-5 0.16 235U 3.6402×10-5 3.6354×10-5 -0.13 101Ru 1.2340×10-5 1.2363×10-5 0.18 236U 2.9331×10-5 2.9372×10-5 0.14 109Ag 5.8054×10-7 5.8184×10-7 0.22 238U 7.4025×10-3 7.4023×10-3 0.00 126Sn 2.0874×10-7 2.0919×10-7 0.22 237Np 1.2708×10-6 1.2799×10-6 0.72 129I 1.6738×10-6 1.6768×10-6 0.18 239Pu 2.9439×10-5 2.9531×10-5 0.31 136Xe 2.9367×10-5 2.9421×10-5 0.18 241Am 5.7110×10-7 5.7058×10-7 -0.09 133Cs 1.4306×10-5 1.4333×10-5 0.19 244Cm 1.1447×10-8 1.1264×10-8 -1.6 注：偏差公式为(N-NSerpent)×100/NSerpent。式中：NSerpent为Serpent计算结果；N为本文计算结果 Note: Deviation formula is (N-NSerpent)×100/NSerpent.NSerpent is the result of Serpent calculation, and N is the result of this paper.

表 1 燃料棒燃耗问题计算结果 Table 1 Results of fuel rod burnup problems.

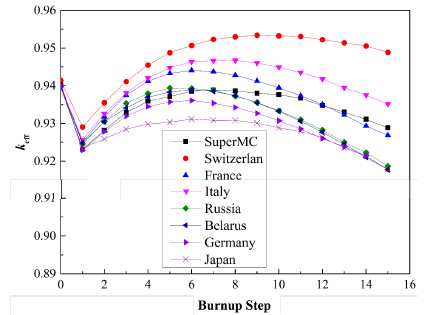
IAEA-ADS基准题模型是一个具有外源的圆柱体结构次临界堆，包括5个材料区，以²³³U为裂变材料，以²³²Th为增殖材料，以Pb为反射层^[1]。本文首先确定在初始k_eff为0.94的情况下，燃料区中²³³U的富集度，然后计算热功率为1500MW时，k_eff随燃耗时间的变化情况，计算结果如图 3所示。计算采用ENDF/B-VII数据库提供的截面、裂变产物和衰变数据。

图 3(Fig.3)

图 3 keff随燃耗步变化 Fig.3 keff variation along with burnup step.

由图 3可见，本文的计算结果处于文献[25]给出的各国计算结果范围内，得到了正确的驼峰曲线，与各国结果的趋势也有比较好的一致性。造成各国计算结果差别的原因之一是使用了不同的数据库，同时，对锕系核素以及裂变产物的处理方式也会对结果产生影响。早期燃耗程序大多对燃耗链进行了简化，只考虑少数几种重要锕系核素，对裂变产物也只考虑Xe、Sm等少数对反应性影响较大的核素，其他产物则采取设置伪裂变产物的方式进行处理，因此在精度上有明显的局限性。而对于ADS及嬗变计算，则需要考虑数十种锕系核素以及上百种裂变产物^[26]。本方法采用精细燃耗链模型，通过遍历初始核素燃耗链，能够基本涵盖并处理ADS系统在燃耗过程中产生的锕系核素以及裂变产物，因此能够达到较高的精度。

同时，为验证桶排序能量查找方法的性能，分别采用三种能量查找方法，使用128种核素进行2×10⁴个粒子的固定源计算。三种方法的时间和内存消耗如表 2所示。从表 2可以看出，统一能量网格方法比常规方法多消耗725.56MB的内存，而本方法仅多消耗30.76MB，较统一能量网格节省了95.7%的内存消耗，而时间性能并未受到影响。由此可以看出，桶排序能量查找方法是对内存要求较高的情况下的一种可行的解决方案。

表 2(Table 2)

表 2 三种能量查找方法性能比较Table 2 Performance comparison of 3 kinds of energy searching methods. 查找方法 Searching method 内存消耗 Memory overhead / MB 运行时间 Running time / min 常规能量 Normal 141.22 121.77 统一能量网格 Union energy grid 866.78 97.99 桶排序 Bucket sort 171.98 94.59

表 2 三种能量查找方法性能比较 Table 2 Performance comparison of 3 kinds of energy searching methods.

本文基于超级蒙特卡罗核计算仿真软件系统SuperMC，采用切比雪夫有理逼近方法和桶排序能量查找方法，进行了内耦合蒙特卡罗燃耗计算的初步研究。通过对燃料棒燃耗例题以及IAEA-ADS基准题的计算，初步证明了本文实现的蒙特卡罗燃耗计算方法的正确性。并且IAEA-ADS基准题的测试结果表明，与统一能量网格方法相比，本方法在保证了计算效率的同时减少了内存开销。本燃耗方法的更多验证和大规模燃耗计算研究将在后续工作中展开。