2. 中国工程物理研究院 中子物理学重点实验室 绵阳 621900
2. Key Laboratory of Neutron Physics, China Academy of Engineering Physics, Mianyang 621900, China
在核物理中,凡涉及到研究中子与原子核相互作用的问题,例如中子与原子核反应截面的测量、中子角分布,就会遇到中子注量密度测量问题。中子通量测量的准确性,直接影响各种参数的准确性。近年来,中子活化分析等技术日益广泛地在各个领域中得到应用。其中中子注量密度的测量是决定分析精度的重要因素。从安全防护的角度出发,对反应堆、加速器周围各处的中子注量密度必需有准确的测量。作为一种最常用的活化材料,115In活化灵敏度高,产物半衰期适中,感生放射性的粒子能量及强度便于测量,被广泛用于快中子注量测量中,因此对其非弹性散射截面的精确测量具有重要意 义[1]。而115In(n,'n) 115mln反应截面,在2.5-6.0 MeV能量内,已有的实验数据差异很大[2, 3, 4]。为澄清分歧,利用四川大学2.5MV静电质子加速器对2.95MeV、3.94MeV、5.24MeV能点的115In中子非弹性散射截面进行了测量。
实验测量中,由靶头材料、冷却水层和样品的包层材料等引起的多次散射效应及注量率衰减效应等均对实验结果产生很大影响。这些因素是实验中不可避免的,也不能通过实验方法加以修正,因此用Monte Carlo程序MCNPX (Monte Carlo N-Particle eXtended)对引起的偏差进行修正计算。
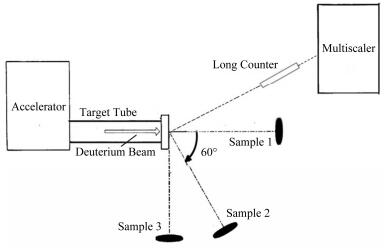
1 实验以197Au的中子俘获截面作为标准,用活化法测量115In的非弹性截面。实验装置示意图如图 1所示。靶管由黄铜制成,靶头用水冷却。利用加速器产生氘束轰击氘靶通过核反应D(d,n)3He产生中子,当出射中子与入射氘束流角度不同时,对应的中子能量如表 1。氘靶用Mo做衬底,先在Mo片上面镀上微米量级的Ti,再用Ti原子吸附D,做成D靶[5]。
| 表1 不同出射角度所对应的中子能量(反应类型D(d,n) 3He,氘束能量2.0MeV) Table 1 Neutron energy of different exit angles (reaction type: D(d,n) 3He,deuterium beam energy is 2.0MeV). |
|
图1 实验装置结构 Figure 1 Schematic layout of the experimental setup. |
实验所用的115In样品为天然金属铟片,其纯度高于 99. 99%。铟有两种同位素:115In的同位素丰度为95.7%,113In的同位素丰度为4.3%。制样时首先将铟片制成直径为 10mm、厚度为 0.5mm的圆片,称重后将4片样品夹在两片厚度为 0.3mm的197Au金箔之间,并将整个样品封装在厚度为 0.3mm的镉盒中,放在与入射氘束流90°的位置。因为197Au对较低能量的中子的活化截面较大,而在90°的位置出射的中子能量相对较低,金箔的作用是测量中子注量。而镉对于热中子的俘获截面大,可吸收绝大部分的热中子,消除大厅低能中子本底影响,以提高实验精确度。在较高能量的中子出射方向0°、60°上样品不加金箔,而根据不同角度出射中子反应微分截面的相互转换得到中子注量。
实验中所用样品架为一外直径为 100mm的铝环,铝环由一圈直径为2mm的铝丝围成。将3个包装好的样品分别放在与入射氘束 0°、60°、90°的位置,以选取不同的照射中子能量。装置中长计数器固定在氘束的另一侧,作为记录中子注量计数的在线监测系统。加速器为2.5MV静电质子加速器,电压在1-2.5MV连续可调,束流的大小可根据实验要求,在纳安到几十微安范围内调节。
样品经过8h照射后,用高纯锗γ谱仪分别测量照射生成的115mIn衰变放出的336.4keV的γ射线和198Au衰变放出的 411.8keV的γ射线全能峰计数,然后以197Au为标准算出115In非弹性散射截面的相对测量值。90°中子注量由式(1)给出:
| ${\phi _{90}} = \frac{{{\lambda _{{\mathop{\rm Au}\nolimits} }}{A_{{\mathop{\rm Au}\nolimits} }}}}{{{N_{{\mathop{\rm Au}\nolimits} }}{\varepsilon _{{\mathop{\rm Au}\nolimits} }}{\sigma _{{\mathop{\rm Au}\nolimits} }}{f_{{\mathop{\rm Au}\nolimits} }}{I_{{\mathop{\rm Au}\nolimits} }}\left( {1 - {{\mathop{\rm e}\nolimits} ^{ - {\lambda _{Au}}{t_{{\mathop{\rm Au}\nolimits} 0}}}}} \right){{\mathop{\rm e}\nolimits} ^{ - {\lambda _{{\mathop{\rm Au}\nolimits} }}{t_{{\mathop{\rm Au}\nolimits} 1}}}}\left( {1 - {{\mathop{\rm e}\nolimits} ^{ - {\lambda _{{\mathop{\rm Au}\nolimits} }}{t_{{\mathop{\rm Au}\nolimits} 2}}}}} \right)}}$ | (1) |
0°、60°的中子注量由式(2)给出:
| ${\phi _\theta } = {\phi _{90}} \cdot \frac{{\sigma (\theta )}}{{\sigma (90)}}$ | (2) |
非弹性散射截面由式(3)给出:
| ${\sigma _{{\mathop{\rm In}\nolimits} }} = \frac{{{\lambda _{{\mathop{\rm In}\nolimits} }}{A_{{\mathop{\rm In}\nolimits} }}}}{{{N_{{\mathop{\rm In}\nolimits} }}{\varepsilon _{{\mathop{\rm In}\nolimits} }}{f_{{\mathop{\rm In}\nolimits} }}{I_{{\mathop{\rm In}\nolimits} }}{\phi _\theta }(1 - {{\mathop{\rm e}\nolimits} ^{ - {\lambda _{{\mathop{\rm In}\nolimits} }}{t_{{\mathop{\rm In}\nolimits} 0}}}}){{\mathop{\rm e}\nolimits} ^{ - {\lambda _{{\mathop{\rm In}\nolimits} }}{t_{{\mathop{\rm In}\nolimits} 1}}}}(1 - {{\mathop{\rm e}\nolimits} ^{ - {\lambda _{{\mathop{\rm In}\nolimits} }}{t_{{\mathop{\rm In}\nolimits} 2}}}})}}$ | (3) |
式中:σ为反应截面;σ(θ)为θ角度出射中子微分截面;φ为中子注量;A为反应产物特征g射线全能峰计数;N为原子核数;ε为特征γ射线全能峰探测效率;λ为反应产物的衰变常数;I为特征γ射线的绝对强度;f为特征γ射线的自吸收修正因子;t0为辐照时间;t1为冷却时间;t2为放射性测量时间;下标In为待测样品;Au为标准样品。实验结果列于表 2中。
| 表2 115ln中子非弹性散射截面实验测量结果 Table 2 Experimental data of neutron inelastic scattering cross section. |
实验值不确定度主要来自高纯锗探测器探测γ射线的效率误差1.5%,金的标准截面误差是1.5%,衰变纲图误差小于1%,实验大厅中子本底误差小于1%,特征γ射线的全能峰统计误差为1%,则总的典型误差是2.5%。
2 多次散射和注量率修正蒙特卡罗方法又称随机抽样技巧或统计实验方法,与一般数值计算方法有很大区别,它是以概率统计理论为基础的一种方法。由于蒙特卡罗方法能够比较逼真地描述事物的特点及物理实验过程,解决一些数值方法难以解决的问题,因而该方法的应用领域日趋广泛[6]。
MCNP(Monte Carlo N-Particle)是由美国洛斯阿拉莫斯国家实验室(Los Alamos National Laboratory)开发的一套模拟中子、光子和电子在物质中输运过程的通用蒙特卡罗计算程序[7]。MCNP具有几何处理能力强、物质反应截面丰富、计算功能全面、可以使用多种减小方差技巧等优点。
在实验过程中氘束轰击到氘靶上,产生的中子按一定比例向四面八方发射。中子经过靶头衬底材料、冷却水层及靶管材料上时,都会使中子发生散射,这样样品中生成的放射性核素有散射中子的干扰贡献。而且当中子打到一定厚度铟活化样品时,会产生注量率随深度变化的自屏蔽效应,使得本实验计算出的中子注量有差异。利用 MCNPX 程序模拟,分别根据需要把上述两个实验装置设成理想条件,用于消除这些效应的影响,并通过和实验条件对比计算多次散射修正因子S和注量修正D。
2.1 中子源的描述使用由MCNPX提供的通用源卡描述中子源。由于氘束轰击到靶上,中子会从一定面积发射,因此模拟过程中我们认为中子是从一个面源发出,源的位置取在靶头的镀膜层。面源最大半径值由SI1 卡输入,用RAD=D1进行抽样。由于中子出射能量与角度有关,首先用SI2 给出多个分立的角度余弦值,然后用DIR=D2进行抽样,用SP2卡给出相关核反应D(d,n)3He的微分截面值作为抽样权重。相应角度上的中子能量由DS3给出,再用ERG FDIR=D3与角度相关的能量进行抽样。
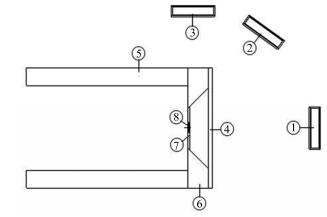
2.2 几何栅元的描述采用图 3所示结构,运用几何栅元卡对其进行详细描述。栅元①②③尺寸为Ø1cm×0.2cm的铟样品,其中③号样品前后包金箔后放置在镉盒里。栅元④为Ø3cm×0.1cm的冷却水层,栅元⑤⑥内充铜材料的靶管,水层紧贴着靶管。⑦为Ø1cm×0.05cm钼底衬,中子源⑧放置在衬底表面。然后把整个实验装置包含在一个大球体内,把球体外的栅元中子源重要性设为0,这样跑出所设范围的中子程序就不再追踪,可以节省计算时间和提高效率。
|
图2 结构示意图 Figure 2 Schematic of the system. |
因在栅元中生成放射性核素的多少可以表示样品铟或金中俘获截面的大小,所以对多次散射进行修正。首先计算真实条件下待测样品In栅元和标样金栅中由俘获反应产生的放射性核素数量N',再用VOID卡将各个包层材料、靶头材料及水层置空,分别得到理想条件下铟样品和金中生成的核素数量 N,由此分别求出待测样品铟和标样金的多次散射修正因子S=N'/N,然后进一步由式(4)计算得到总的多次散射修正因子。
| $S = {S_{{\mathop{\rm In}\nolimits} }}/{S_{{\mathop{\rm Au}\nolimits} }}$ | (4) |
程序用F4:n T与Fm4 C 3 51卡相结合,实现对于铟样品或标样金,通过中子非弹性散射反应生成的放射性核素的计数,其中51为FM4卡调用 ENDF (Evaluated Nuclear Data File)中非弹性散射反应的反应号,俘获反应的反应号为102℃为样品栅元中115In(标样Au中为197Au)的原子密度,默认为-1;通过F4卡得到通过栅元T中的中子注量。
2.4 计算注量率衰减因子D将铟样品所在栅元沿中子入射方向划分成m份等体积的微栅元。设这m个微栅元生成的核素计数分别为NIn、NIn、…、NIn、…、NIn,则待测样品的衰减修正因子为:
| ${D_{{\mathop{\rm In}\nolimits} }} = \frac{{\sum\limits_{i = 1}^m {{N_{{{{\mathop{\rm In}\nolimits} }_i}}}} }}{{{N_{{{{\mathop{\rm In}\nolimits} }_1}}} \cdot m}}$ | (5) |
式中:NIn表示第i (1≤i≤m)个微栅元中生成核素的多少;NIn·m表示第1个微栅元中生成放射性核素的m倍,其中m取得越大,也就是栅元分得越小结果越精确,本文中m取10。
2.5 修正结果利用MCNPX程序分别计算多次散射修正因子 S和注量衰减因子D,然后求出总的修正因子F=S·D。将总的修正因子F与实验得到的中子注量值相乘即得到修正值。现将修正所得结果列于表 3。
| 表3 115ln(n,'n) 115mln反应截面的修正值(反应类型D(d,n)3He) Table 3 Modified values of 115ln(n,'n) 115mln cross sections (reaction type: D(d,n)3He). |
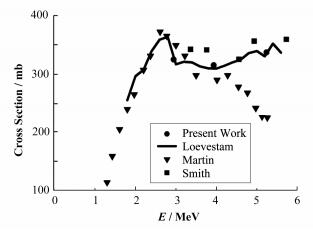
由表 3可以看出,在本文的实验条件下,最大修正量约为5%,可见实验中的多次散射和自屏蔽效应不可忽略。当然,实验中可以通过减小靶管、靶底衬、水层及样品和包层材料等厚度来减小多次散射效应和自屏蔽效应的影响。图 3为本文结果与现有其他实验数据或理论计算值的比较。
|
图3 115In中子非弹性散射截面 Figure 3 Neutron inelastic scattering cross section of 115ln. |
由图 3可见,本文的结果与Loevestam[2]的计算值符合较好;Smith[3]截面曲线走向虽然与本文的一致但是明显高于本文;而在小于4MeV能区,Martin[4]的结果在误差范围和本文一致,但大于4MeV能区比本文结果低很多。
| [1] | 吴治华. 原子核物理实验方法[M]. 北京:高等教育出版社, 1997 WU Zhihua. Experimental method of nuclear physics[M]. Beijing:Higher Education Press, 1997( 1) 1) |
| [2] | Loevestam G, Hult M, Fessler A. Measurement of neutron excitation functions using wide energy neutron beams[J]. Nuclear Instruments & Methods in Physics Research, 2007, A580(3):1400-1409. DOI:10.1016/j.nima. 2007.06.090( 2) 2) |
| [3] | Smith D L, Meadows J W. Fast neutron excitation of isomeric states of indium[J]. Nuclear Science and Engineering, 1976, 60:319-322. DOI:10.13182/NSE76-2( 2) 2) |
| [4] | Martin H C, Diven B C, Taschek R F. Cross sections for production of In115m and Au197m by inelastic scattering of neutrons[J]. Physical Review, 1954, 93(1):199-204. DOI:10.1103/PhysRev.93.199( 2) 2) |
| [5] | 史淑廷, 罗小兵, 王磊. 98Mo中子俘获截面的实验测量及Monte Carlo修正[J]. 清华大学学报, 2007, 47(S1):1076-1080 SHI Shuyan, LUO Xiaobing, WANG Lei.Experimental measurement and Monte Carlo correction of neutron capture cross section of 98Mo[J]. Journal of Tsinghua University, 2007, 47(S1):1076-1080( 1) 1) |
| [6] | 许淑艳. 蒙特卡罗方法在实验核物理中的应用[M]. 北京:原子能出版社, 1996 XU Shuyan. The using of Monte Carlo methods in experimental nuclear physics[M]. Beijing:Atomic Energy Publishing Company, 1996( 1) 1) |
| [7] | 裴鹿成, 王仲奇. Monte Carlo方法及其应用[M]. 北京:海洋出版社, 1998:122 PEI Lucheng, WANG Zhongqi. Monte Carlo method and its application[M]. Beijing:Ocean Publishing Company, 1998:122( 1) 1) |


