2. 中国工程物理研究院 研究生院 北京 100088
2. Graduate School, China Academy of Engineering Physics, Beijing 100088, China
利用反中微子探测核反应堆运行和核材料生产是近几年新兴的核查与防扩散技术。该技术抗干扰性强,不具有入侵性,不要求与反应堆连接,可实现对反应堆运行状况的远程监测。将来还可以用于任何人为裂变进程的监测,比如《全面禁止核试验条约》(Comprehensive Nuclear-Test-Ban Treaty,CTBT)等条约的现场核查,以及对海军堆燃料的探测等[1]。
通过对反应堆核材料出射反中微子的测量,可以获得反应堆停堆、功率调整以及卸料等信息。在裂变过程中,平均每次原子核裂变会产生约6个反中微子,反中微子数量与反应堆内裂变发生次数相关。因而检测反应堆产生的反中微子强度变化,可以提供反应堆运行状况信息。另外,239Pu和238U裂变产生反中微子的能谱具有不同分布特征,导致探测器对两类反中微子的平均探测效率存在差异。对探测到的反中微子强度和反应堆功率的联合分析还可以提供与反应堆内Pu材料含量相关的信息[1]。
利用反中微子监测反应堆运行的概念最早由Mikaélyan等[2]提出,并进行了初步的实验验证。2007年Sowden等[3]联合发表文章,介绍了由美国圣地亚国家实验室和劳伦斯·利弗摩尔国家实验室联合开展的利用反中微子监测反应堆运行的实验。该实验通过对美国圣·奥诺弗雷商用反应堆10年的监测,检验了反中微子对反应堆运行状况的监测能力。研究结果表明,反中微子探测器的探测结果可以反映出反应堆的运行情况。通过分析1-3 h内的计数变化,可以判断出反应堆运行状态的变化;通过分析7 d探测的平均计数,可以判断出反应堆2%-3%的热功率变化。对探测结果的分析可以反映出反应堆更换燃料棒的过程。该实验结果在国际原子能机构(International Atomic Energy Agency,IAEA)举办的研讨会上报告后,引起了国际社会的广泛关注[4]。多个具有反中微子探测经验的实验室开始研发相关探测系统、开展相关研究工作[5, 6]。我国在反中微子探测领域位于世界领先水平,也开展了利用反中微子监测反应堆的理论研究[7, 8, 9]。
为深入开展利用反应堆出射反中微子监测反应堆的研究,我们在中国工程物理研究院战略研究中心开发的弹头认证数值模拟平台[10]的基础上,增加了数值模拟软件对反中微子生成、输运、探测过程的数值模拟软件,实现了对探测反应堆出射反中微子过程的数值模拟。利用这个软件,我们模拟了反应堆运行期间反中微子探测结果与反应堆内核材料组成的关系。数值模拟结果表明,反中微子强度可以反映出反应堆的运行状况,在反应堆等功率运行时反中微子强度的探测结果与堆内钚材料的累计具有明确关系。
1 利用反中微子监测反应堆运行物理机制反应堆的运行伴随着裂变材料的裂变过程,反中微子的产生过程与反应堆的裂变过程相关,因而通过探测反应堆出射反中微子可以获得反应堆中核材料发生裂变的信息。
1.1 应堆反中微子的产生反应堆的运行伴随着裂变材料的裂变过程,反中微子的产生过程与反应堆的裂变过程相关,因而通过探测反应堆出射反中微子可以获得反应堆中核材料发生裂变的信息。
由于重原子核中子质子比大于中等质量原子核,在重核裂变后一些中子出射,诱发新的裂变;还有一些多余的中子则留在裂变碎片中,通过β衰变变成质子,使裂变碎片更接近稳定。而β衰变过程中会伴随着反中微子的产生。如:
| ${{\text{A}}^{\text{Z}}}\to {{(\text{A}+\text{1)}}^{\text{Z}}}+{{\text{e}}^{-}}+{{\bar{\nu }}_{\text{e}}}$ | (1) |
因此,反应堆中的重原子裂变过程伴随着反中微子的产生,平均每次裂变能够产生大约6个反中微子[11]。产生反中微子的裂变反应很多,比如:
| $\begin{align} & \text{ U+n}\to {}^{\text{94}}\text{Kr+}{}^{\text{140}}\text{Ba+2n+200 MeV} \\ & \bullet {}^{\text{140}}\text{Ba}\to {}^{\text{140}}\text{La(}{{\text{ }\!\!\beta\!\!\text{ }}^{-}}\text{,13 d,1 MeV)} \\ & \text{ }{}^{\text{140}}\text{La }\to \text{ }{}^{\text{140}}\text{Ce(}{{\text{ }\!\!\beta\!\!\text{ }}^{-}}\text{,40 h,2}\text{.2 MeV)} \\ & \bullet {}^{\text{94}}\text{Kr }\to \text{ }{}^{\text{94}}\text{Rb(}{{\text{ }\!\!\beta\!\!\text{ }}^{-}}\text{,0}\text{.2 s,7}\text{.5 MeV)} \\ & \text{ }{}^{\text{94}}\text{Rb }\to {}^{\text{94}}\text{Sr(}{{\text{ }\!\!\beta\!\!\text{ }}^{-}}\text{,2}\text{.7 s,10 MeV)} \\ & \text{ }{}^{\text{94}}\text{Sr }\to \text{ }{}^{\text{94}}\text{Y(}{{\text{ }\!\!\beta\!\!\text{ }}^{-}}\text{,75 s,3}\text{.4 MeV)} \\ & \text{ }{}^{\text{94}}\text{Y }\to \text{ }{}^{\text{94}}\text{Zr(}{{\text{ }\!\!\beta\!\!\text{ }}^{-}}\text{,19 min,4}\text{.9 MeV)} \\ \end{align}$ | (2) |
在反应堆中,不断有类似的反应发生,产生大量反中微子。对于铀和钚材料,平均每次裂变能够产生约200 MeV能量。也就是说,对于一个功率3000 MW的反应堆,每秒钟可以产生约1022个反中微子。
1.2 反中微子探测大多反中微子探测器都是基于反中微子与质子相互作用产生正电子的反β衰变反应实现,即:
| ${{\bar{\nu }}_{\text{e}}}+\text{p}\to {{\text{e}}^{+}}+\text{n}$ | (3) |
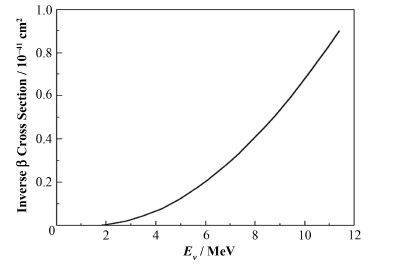
反β衰变反应截面与反中微子能量有关,根据文献[12]中的测量结果,能量较高的反中微子具有较大反应截面,如图 1所示[12]。
|
图 1 反β反应截面图 Fig.1 Inverseβ decay cross section. |
反β衰变反应的反应截面很小,为增加反中微子探测计数,在探测器中,一般用大量的水增加反β衰变计数。在探测器中,e+与e-发生反应产生两个能量511 keV的光子,通过探测末态能量为511keV的光子和中子信号及其时间关联,可以判断反β反应的发生。世界上,主要的反中微子探测器都是基于这一原理实现的,比如Reines和Cowan的实验组[13],以及CHOOZ实验[14],Palo Verde实验[15]和大亚湾实验[16]。能量小于反应阈值的反中微子不能诱发β衰变反应,无法用这种方法进行探测,其能量阈值为1.806 MeV[12]。
另外,由于反中微子探测在理论和实验上都具有重要意义,很多学者不断提出新的反中微子探测方法,试图提高反中微子的探测效率,但这些方法还未能用于实践。学术界,特别是防扩散核查技术研究领域的学者,对研制具有更高探测效率的反中微子探测装置充满期待[9]。
1.3 235U和239Pu出射反中微子的差异反应堆中主要的裂变核素235U和239Pu核素,具有不同的裂变产物分布,因而β衰变母核不同,导致出射反中微子具有不同的能量分布。文献[17]中展示了几种重要裂变核素的不同反中微子能谱。
由于235U裂变出射的反中微子平均能量较高,而探测器对高能反中微子的探测效率较高,因而等功率下235U材料较多的燃料对应反中微子的探测量较多。
2 反中微子数值模拟通过对现有数值模拟软件的改造,我们实现了对反中微子产生和探测过程的数值模拟。我们在数值模拟软件中增加了核素裂变信息的输出和处理。
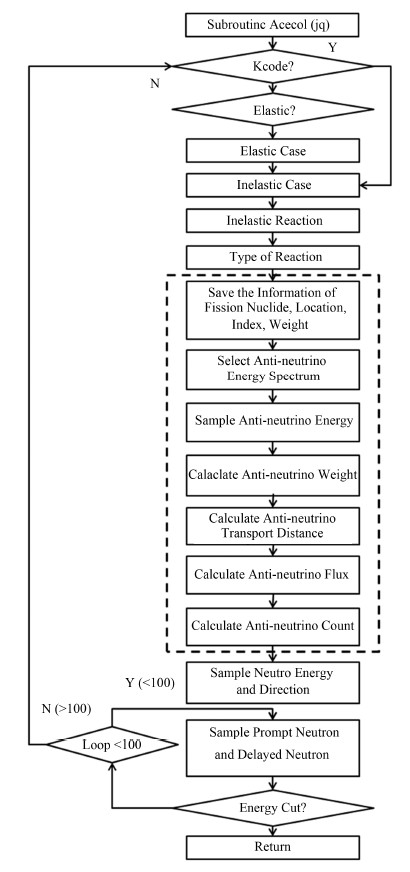
2.1 对裂变产生反中微子过程的模拟在原有程序中每次调用中子与物质相互作用的子程序时,增加了“为反中微子计算读取裂变核、裂变反应编号、位置、中子权重信息”的子程序,以获得核裂变反应信息,再根据核裂变信息确定探测器响应,如图 3所示。图 3中虚框内为本程序增加的流程。
|
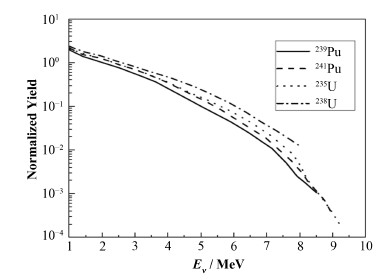
图 2 238U、235U、239Pu和241Pu裂变产生的反中微子能谱 Fig.2 Anti-neutrino energy spectra of 238U, 235U, 239Pu and 241Pu. |
|
图 3 模拟反中微子产生的程序流程 Fig.3 Program flow diagram of anti-neutrino production. |
程序中利用蒙特卡罗方法确定出射反中微子能量。在程序运行前,预先将图 2在1-10 MeV的反中微子能谱分成100群,对不同裂变核素分别建立多群反中微子能量参数库Yg。在计算过程中,首先根据裂变核素选取相应数据库Yg,再抽取(0,1]间均匀分布的随机变量ξ,式(4)确定反中微子所在能群,最终确定出射反中微子能量E。
| $\sum\limits_{g=0}^{n}{{{Y}_{g}}}<\xi \le \sum\limits_{g=0}^{n+1}{{{Y}_{g}}}$ | (4) |
式中:g为多群反中微子能量的群参数;Yg为反中微子能量概率分布函数。
2.2 对反中微子输运和探测过程的模拟在计算反中微子通量时,根据距离计算出射角分布均匀的反中微子在被测区域位置的通量:
| ${{\phi }_{\nu d}}(E,{{\vec{r}}_{d}})={{\eta }_{\nu }}(E)\int_{V}{\frac{{{s}_{d}}}{{{(\vec{r}-{{{\vec{r}}}_{d}})}^{2}}}{{n}_{f}}(\vec{r})\text{d}\vec{r}}$ | (5) |
式中:${{\phi }_{\nu d}}(E,{{\vec{r}}_{d}})$、分别表示${{\vec{r}}_{d}}$位置探测器反中微子通量和探测器截面积;${{n}_{f}}(\vec{r})$、和V为反应堆内$\vec{r}$处裂变速率、裂变反应产生的某能量反中微子和反应堆体积。
某时刻探测器响应根据反中微子能量和探测器响应函数得到。
| $C(t)={{\varepsilon }_{\text{n}{{\text{e}}^{+}}}}{{\Sigma }_{\text{Ei}}}{{n}_{\text{Ei}}}(t)$ | (6) |
式中:${{\varepsilon }_{\text{n}{{\text{e}}^{+}}}}$、${{\Sigma }_{\text{Ei}}}$、${{n}_{\text{Ei}}}(t)$分别为探测器对中子和正电子关联探测效率、能量处于Ei能群反中微子与质子反应截面和该时刻计入探测区域的反中微子数。
2.3 探测反应堆出射反中微子的数值模拟利用战略研究中心开发的弹头认证技术数值模拟平台,将反中微子计算程序与杨俊云等[18]开发的MCORGS软件耦合,实现了在模拟反应堆运行过程中计算出射反中微子的功能。可用于计算商用反应堆、聚变裂变混合堆等核材料体系的燃耗。MCORGS软件利用MCNP5程序计算中子通量和燃耗计算需要的转换截面;利用ORIGENS求解燃耗方程[19]。
MCNP程序是由美国洛斯阿拉莫斯国立实验室编制的通用三维Monte Carlo输运计算软件,可实现三维复杂几何系统中的中子-光子耦合输运问题的数值模拟。ORIGEN程序是由美国橡树岭国立实验室编制的点堆燃耗计算程序,可模拟核反应堆燃料燃烧过程。数值模拟主要在于确定核燃料成份随时间的变化关系以及核反应堆的反应性随燃耗深度的变化关系,其核素随时间的变化可由如下的燃耗方程描述:
| $\begin{align} & \frac{\text{d}{{N}_{i}}}{\text{d}t}=\sum\limits_{j}{Y_{i}^{j}\sigma _{f}^{j}{{N}^{j}}\varphi }+\sigma _{c}^{i-1}{{N}^{i-1}}\varphi+\\ & _{{}}^{{}}\lambda _{i}^{'}N_{i}^{'}-\sigma _{a}^{i}{{N}_{i}}\varphi -{{\lambda }_{i}}{{N}_{i}} \end{align}$ | (6) |
式中:i=1,2,3,…,I,是裂变产生核素的序号;Yij为j种核裂变生成的i种核素的产额;σij为j种核的裂变截面;σci为i种核的俘获截面;σai为i种核的吸收截面,包括俘获、裂变、2n、3n等截面;λi为i种核的衰变常数;Ni'为i种核激发态的核数;λi'为i种核的激发态到基态的衰变常数。
由标准程序MCNP和ORIGEN耦合而成的MCORGS软件系统可以模拟各种类型复杂几何结构核系统的燃料燃耗过程,进而分析燃料元件和乏燃料元件的核素成份。
3 对SONGS1实验的数值模拟本工作对软件的修改是基于MCNP软件,该软件在模拟中子输运问题上较为权威[20]。对软件的修改主要是提取了原程序中的一些过程量,并利用这些过程量通过确定的算法获得反中微子结果。这些修改的物理意义明确,在确保程序正确的基础上可以信任对软件的修改。利用我们修改的数值模拟软件,我们对美国SONGS1实验进行了数值模拟。该实验是美国圣地亚国家实验室和劳伦斯·利弗摩尔国家实验室联合进行的。实验小组利用反中微子探测对美国圣·奥诺弗雷商用反应堆进行了10年的监测,检验了反中微子对反应堆运行状况的监测能力[5]。该实验检验了反应堆燃耗、反应堆产生钚材料丰度与反中微子计数关系。
实验探测的商用反应堆热功率为3000 W,该反应堆每秒钟发生约1021次裂变;探测器位于距离堆芯25 m的地下,每天有1017个反中微子经过探测器;实验使用体积640 L的液体闪烁体探测器,每天可以获得400多次可探测信号。
我们模拟采用的反应堆为运行功率3000 MW的压水堆。反应堆建模利用反射边界条件对单棒建模实现。探测区域距离探测器25 m,与反中微子发生反应的材料为有效探测面积0.8 m2、厚度0.8 m的纯水。该探测器对穿过探测区域反中微子的平均探测效率约为2.5×10-18。
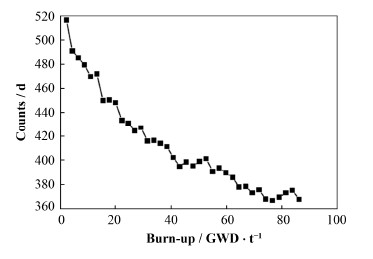
由于SONGS1实验报告并没有给出反应堆燃料同位素构成,我们利用数值模拟平台,计算了不同燃耗深度下,运行功率为3000 MW压水堆燃耗与出射反中微子计数之间的联系,如图 4所示。在反应堆运行初期,燃耗较少时,探测器平均每天探测到的反中微子数约为500;当燃耗逐渐增加,每天探测到的反中微子数逐渐降至400以下。
|
图 4 核燃料燃耗深度与出射反中微子计数变化关系 Fig.4 Relation between anti-neutrino counts and reactor burn-up. |
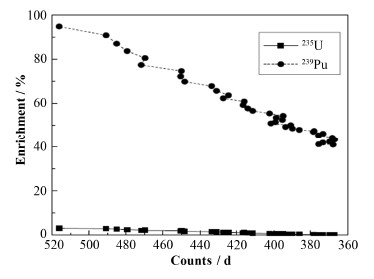
文献[5]认为可以通过对反中微子的探测实现对核材料同位素丰度的监测。我们也绘制了反应堆不同燃耗下,出射反中微子计数与反应堆内铀、钚材料同位素比之间的关系,如图 5所示。数值模拟结果表明,在反应堆等功率运行的条件下,出射反中微子个数与反应堆内235U和239Pu同位素含量成线性关系。出射反中微子计数可以提供钚材料同位素含量相关信息。
|
图 5 反中微子计数与235U、239Pu同位素含量变化关系 Fig.5 Relation between anti-neutrino counts and 235U, 239Pu isotope abundances. |
在模拟的反应堆运行过程中,随反应堆燃耗增加,不断有铀材料吸收中子产生钚材料,235U的含量降低,而 239Pu含量增加。在反应堆按照相同功率运行的情况下,单位时间的总裂变数几乎不变,但其中由于239Pu的中子反应截面大于235U,因此参与裂变的239Pu逐渐增多。正如图 2所示的235U和239Pu裂变出射反中微子能谱,235U对应平均出射反中微子能量较高。根据图 1所示的反中微子诱发反β反应的反应截面,探测器对高能中子的探测效率较高,因此当反应堆内239Pu增加时,等功率下出射反中微子计数下降。
4 反中微子计数与反应堆运行状况为验证利用反中微子监测反应堆的能力,我们进一步研究了反应堆运行情况对反中微子计数的影响,如反应堆停堆与降低功率运行等。我们模拟了反应堆在满功率运行、降功率运行和停堆状况下,出射反中微子的探测状况。反应堆的运行情况如表 1所示。在模拟过程中,为集中讨论运行功率对结果影响,没有考虑反应堆换料过程。
| 表 1 模拟的反应堆运行情况 Table 1 Operation model of the simulated reactor. |
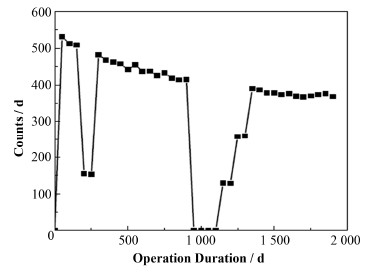
模拟得到的出射反中微子随时间变化如图 6所示。在降功率运行期间,出射反中微子数目也比满功率运行时相应降低。在停堆时,出射反中微子接近于零。
|
图 6 反应堆运行情况下出射反中微子计数随时间变化 Fig.6 Relation between anti-neutrino counts and time under reactor operation and shutdown. |
为讨论停堆换料对出射反中微子计数的影响,我们分别模拟得到了两种换料形式下,出射反中微子强度随时间变化的结果,两种换料方式见表 2,它们分别描述正常规律换料和频繁换料的情况。表 2中换料周期为两次换料之间的时间。换料比为在反应达到既定运行天数后用新燃料换掉的乏燃料占总燃料的比例。
| 表 2 模拟的反应堆换料模式 Table 2 Simulated reactor refueling models. |
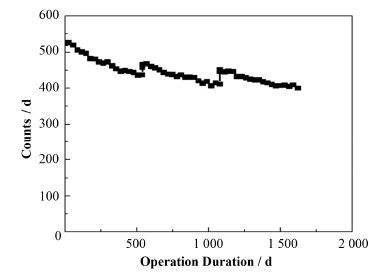
正常换料下,反应堆出射反中微子计数如图 7所示。在初装料(0-540 d)后,随239Pu存量的增加反中微子计数降低。经过换料,239Pu存量下降后出射反中微子计数忽然增加(540 d和1080 d)。
|
图 7 反应堆正常换料情况下反中微子出射计数随时间变化 Fig.7 Relation between anti-neutrino counts and time under normal refueling. |
在频繁换料情况下,由于反应堆燃料燃耗不深,239Pu对整个堆功率的贡献不多,因而出射反中微子计数并未发生显著变化。
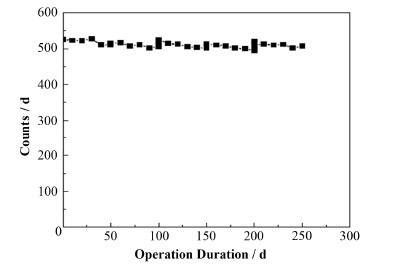
|
图 8 反应堆频繁换料情况下反中微子出射计数随时间变化 Fig.8 Relation between anti-neutrino counts and time under frequently refueling. |
在反应堆频繁换料情况下,由于燃料的燃耗较浅,尽管卸除的燃料中239Pu含量较少,但其同位素含量较高,更适宜用作核武器材料。监测反应堆是否有违规的武器级钚材料生产是防扩散监测的一个重要目的,通过对出射反中微子的监测,可以区分正常换料和频繁换料。
此外,如果在换料时不按照正常模式更换燃料较深的燃料棒,而更换燃耗较浅的燃料,也可以获得更接近于武器级的钚材料。通过对出射反中微子计数的监测也可以发现这种行为。
5 结语利用反中微子监测反应堆的方法具有抗干扰性强、入侵性低等优势,是未来防扩散、监督裂变材料生产的可能手段。中国工程物理研究院战略研究中心通过拓展已有弹头认证数值模拟平台的功能,建立了数值模拟研究反应堆出射反中微子的模拟软件,实现了对利用反中微子监测反应堆过程的数值模拟,并研究了该方法在监测核材料生产、反应堆运行以及不违约活动等领域应用的能力和有效性。
利用对美国SONGS1实验系统结果的模拟和比较,我们对研发的反应堆出射反中微子探测软件进行了验证。结果表明,数值模拟软件对出射反中微子计数的计算结果与实验结果一致。利用该软件研究了反应堆燃耗与出射反中微子计数间的关系,不同燃耗下铀和钚材料同位素比与出射反中微子计数之间的关系,以及不同反应堆运行和换料条件下出射中子随反应堆运行时间的变化规律。模拟结果表明,出射反中微子计数可以反映出反应堆的运行状况;当反应堆运行功率已知时,出射反中微子数目还可以反映出反应堆内钚材料的沉积情况。开展利用反中微子监测反应堆的研究,不仅能为建立利用反中微子探测核反应堆的技术能力提供理论基础,还能为反中微子探测技术提供可能的应用前景。
| 1 | Bernstein A, Wang Y, Gratta G, et al. Nuclear reactor safeguards and monitoring with antineutrino detectors[J]. Journal of Applied Physics, 2002, 91:4672-4676. DOI:10.1063/1.1452775( 1) 1) |
| 2 | Korovkin V A, Kodanev S A, Panashchenko N S, et al. Measuring nuclear plant power output by neutrino detection[J]. Atomic Energy, 1988, 65(3):712-718( 1) 1) |
| 3 | Klimov Y V, Kopeikin V I, Mikaélyan L A, et al. Neutrino method remote measurement of reactor power and power output[J]. Atomic Energy, 1994, 76(2):123-127( 1) 1) |
| 4 | Bowden N, Bernsteinb A, Allen M, et al. Experimental results from an antineutrino detector for cooperative monitoring of nuclear reactors[J]. Nuclear Instruments and Methods in Physics Research Section A:Accelerators, Spectrometers, Detectors and Associated Equipment, 2007, 572:985-998( 1) 1) |
| 5 | Bowden N. Reactor monitoring and safeguards using antineutrino detectors[J]. Journal of Physics:Conference Series, 2008, 136:022008( 3) 3) |
| 6 | Classen T, Berustein A, Bowden N S, et al. Development of an advanced antineutrino detector for reactor monitoring[J]. Nuclear Instruments and Methods in Physics Research A, 2015, 771:139-146. DOI:http://dx.doi.org/10.106/J.nima.2014.10.022( 1) 1) |
| 7 | Zhong S Q, Ren X M, Huang Y Q, et al. Numerical studies on flow and thermal fields in MOCVD reactor[J]. Chinese Science Bulletin, 2010, 55(6):560-566. DOI:10.1007/s11434-009-0590-8( 1) 1) |
| 8 | 梁静, 董岚, 罗涛, 等. 大亚湾中微子实验反应堆至探 测器三维距离的测量[J]. 核技术, 2014, 37(1):010602. DOI:10.11889/j.0253-3219.2014.hjs.37.010602 LIANG Jing, DONG Lan, LUO Tao, et al. Measurement of 3D distance from nuclear reactors to detectors in Daya Bay reactor neutrino experiment[J]. Nuclear Techniques, 2014, 37(1):010602. DOI:10.11889/j.0253-3219.2014. hjs.37.010602( 1) 1) |
| 9 | Hao H F, Liang H, Zheng L, et al. Development of VME system in RPC electronics for reactor neutrino experiment at Daya Bay Nuclear Power Plant[J]. Nuclear Science and Techniques, 2013, 24:010401. DOI:10.13538/j.1001-8042/nst.2013.01.002( 2) 2) |
| 10 | 朱剑钰, 谢文雄, 李刚, 等, 核查技术数值实验平台中 的时间关联符合测量与中子多重性测量[J]. 计算物理, 2015, 32(2):213-219. DOI:1001-246X(2015) 02-0213-07 ZHU Jianyu, XIE Wenxiong, LI Gang, et al. Time correlation and neutron multiplicity counting measurement in numerical experiment platform on verification technologies[J]. Chinese Journal of Computational Physics, 2015, 32(2):213-219. DOI:1001-246X(2015) 02-0213-07( 1) 1) |
| 11 | Bemporad C, Gratta G, Vogel P, et al. Reactor-based neutrino oscillation experiments[J]. Reviews of Modern Physics, 2002, 74:297-328( 1) 1) |
| 12 | Vogel P. Analysis of the antineutrino capture on protons[J]. Physical Review D, 1984, 29:1918-1928( 2) 2) |
| 13 | Reines F, Cowan C L. Detection of the free neutrino[J]. Physics Review, 1953, 92:830-831( 1) 1) |
| 14 | Apollonio M, Baldini A, Bemporad C, et al. Search for neutrino oscillations on a long base-line at the CHOOZ nuclear power station[J]. The European Physical Journal C, 2003, 27:331-374( 1) 1) |
| 15 | Boehm F, Busenitz J, Cook B, et al. Final results from the Palo Verde neutrino oscillation experiment[J]. Physical Review D, 2001, 64:112001( 1) 1) |
| 16 | An F P, Balantekin A B, Band H R, et al. Measurement of the reactor antineutrino flux and spectrum at Daya Bay[J]. Physical Review Letters, 2015, 116:061801. DOI:http://dx.doi.org/10.1103/PhysRevLett.116.061801( 1) 1) |
| 17 | An F P, Balantekin A B, Band H R, et al. Measurement of the reactor antineutrino flux and spectrum at Daya Bay[J]. Physical Review Letters, 2015, 116:061801. DOI:http://dx.doi.org/10.1103/PhysRevLett.116.061801( 1) 1) |
| 18 | 杨俊云, 师学明, 应阳君. 激光惯性约束聚变裂变混合 能源包层中子学数值模拟[J]. 原子能科学与技术, 2015, 49(11):1961-1965 YANG Junyun, SHI Xueming, YING Yangjun. Numerical simulation on blanket neutroics of laser inertial confinement fusion-fission energy[J]. Atomic Energy Science and Technology, 2015, 49(11):1961-1965( 1) 1) |
| 19 | 师学明, 张本爱. 输运与燃耗耦合程序MCORGS 的开 发[J]. 核动力工程, 2010, 31(3):1-4. DOI:0258-0926 (2010)03-0001-04 SHI Xueming, ZHANG Ben'ai. Development of transport-burnup code MCORGS[J]. Nuclear Power Engineering, 2010, 31(3):1-4. DOI:0258-0926(2010) 03-0001-04( 1) 1) |
| 20 | X-5 Monte Carlo Team. MCNP-a general Monte Carlo N-particle transport code[R]. Version 5. LA-13422-M, Los Alamos National Laboratory, 1998( 1) 1) |
