2. 中国科学院大学 北京 100049;
3. 上海联影医疗科技有限公司 上海 201807
2. University of Chinese Academy of Sciences, Beijing 100049, China;
3. Shanghai United Imaging Healthcare Corporation, Shanghai 201807, China
正电子发射型断层显像仪(Positron Emission Tomography,PET)的探测器通常由闪烁晶体阵列耦合光电转换器件的结构组成。闪烁晶体接收成像过程中湮灭事件产生的γ光子对,并将其转化为可见光;光电转换器件接收到这些光信号之后将其转换为相应的电信号,并进行放大输出给后端电路处理。理想情况下,接收湮灭效应γ光子的晶体阵列的物理位置和解码到图像上位置的对应关系应该是线性关系。但是,由于编解码过程中的康普顿散射效应、各晶体条的物理材质不均一以及相关电子元器件的非线性响应等原因[1],导致两者的对应呈非线性关系。γ光子入射位置探测的准确性是保证PET系统图像高分辨率的前提。为准确找到两者之间的对应关系,传统的做法是建立两者之间的位置对应表,即晶体查找表。
建立晶体查找表通常都是基于描述γ光子入射事例数的二维位置直方图(Flood histograms,以下简称二维位置直方图),它是由模拟湮灭事件的放射源向不同方向均匀照射PET探测器所产生的,每个点的像素值正比于该点接收到的光子数[2]。理论上,二维位置直方图上的一个亮斑块对应一个闪烁晶体检测到的入射事件,建立晶体查找表即找到所有闪烁晶体与二维位置直方图中亮斑块间的对应关系。
现有晶体查找表的建立以自动绘制算法为主,人工检查修正为辅。自动绘制晶体查找表的算法可大致分为三类:晶体中心检测法、晶体行列检测法和晶体边界检测法。晶体中心检测法大都通过检测晶体中心来初步定位晶体位置,并结合其空间信息确定每个位置实际对应的晶体,然后结合图像的拓扑信息和能量信息对晶体阵列进行边界分割。由于理论上越靠近晶体中心位置像素亮度值越大,寻找晶体的中心位置往往等价于在二维图像域上寻峰,代表性的算法有二维高斯混叠模型(Gaussian Mixture Model,GMM)[3],该算法优点是能够很好地应对晶体阵列的整体形变,但易受黏连点、伪影和图像灰度不均匀的影响,且运算复杂度随晶体数量呈指数上升,晶体数量大的时候该方法并不适用。基于PCA回归算法[4],通过训练样本数据提供更优的初始位置,减少了优化时间,并尽可能地保证获取全局最优解。更新颖的连续非极大值衰退法[5]可以以更快的速度完成二维寻峰,且对黏连点和伪影的处理效果相对更好,但对图像预处理结果很敏感。晶体行列检测法先检测晶体排列成行和列的大致位置,再通过行列交叉位置反推晶体位置,常见的方法如基于投影的高斯拟合算法[6]和基于傅里叶变换的非刚性配准法[7]。该类算法大都基于晶体阵列为方形的特征,所以不易受伪影影响,但对晶体阵列整体形变和行列扭曲比较敏感。晶体边界检测法通过寻找晶体或晶体行列的边界特征直接对晶体块进行分割,如分水岭算法,该算法容易造成过分割的问题,邻域标准差算法[8]和基于模板的分割方法[9]等算法结果相对更鲁棒,但不能很好地处理晶体黏连严重的情况。
综上所述,已有的众多晶体检测算法往往能在某种类型的二维位置直方图上满足自动化检测的要求,但它们各自的局限性使其无法在不同的二维位置直方图上保证算法的鲁棒性。特别是对于高分辨率PET探测器来说,二维位置直方图上呈现的晶格阵列不规则问题众多,晶体数量又庞大,即使部分晶体分割出错,依然需要耗费大量的人力来手动修正。在已有的晶体检测算法中很难找到一种算法一次性解决所有的问题,获得工业界所需要的晶体分割准确率。在此背景下,本文提出一种基于多种探测算法结果分级融合的PET探测器晶体检测算法(以下简称多探子融合算法),该算法以已有的晶体检测算法为基础,利用不同晶体检测算法在结果上的相似性和互补性,对每个探测结果的置信度划分等级,按置信度由高到低分级依次处理,最大程度地减少错误探测的数量。多探子融合算法经大规模实验数据结果验证,在鲁棒性方面对比单一检测算法优势明显。
1 数据说明本项目对上海联影医疗科技有限公司提供的三台PET仪器产生的二维位置直方图数据进行了算法结果测试,分别称为PET1、PET2、PET3,分别对应有432、432、420张二维位置直方图。如图 1所示,所有二维位置直方图的规格都是256×256(像素),每张二维位置直方图对应一个晶体阵列,每个晶体阵列单元中有16×16共256个晶体,每个晶体的物理尺寸为2.3 mm×2.3 mm。PET1是三组数据中质量最好的,晶体阵列相对最规整(图 1(a));PET2晶体阵列的行列扭曲问题非常严重(如图 1(b)椭圆框标识的位置);PET3图像噪声特别大,信噪比很低(如图 1(c)椭圆框标识的位置)。

|
图 1 不同数据集的二维位置直方图对比 Fig.1 Illustrations of flood histograms of different levels of quality. |
本文所说的融合是以单个晶体为单位,对不同探测算法得到的探测结果进行有机的整合。现有的晶体探测算法各有局限性,对同一二维位置直方图,各算法的探测结果中正确的晶体往往是相近的,但出错的晶体不尽相同。基于此前提,对同一晶格的探测,不同算法之间得出的结果越相似说明此结果越可信。各算法本身的性能和不同算法之间的互补程度将对融合算法的结果造成一定的影响,单一算法的鲁棒性是融合后结果的性能基础,而算法之间的互补性强,取长补短,才能得到比单一探测算法鲁棒性更强的结果。在本算法的实现中,我们选取了连续非极大值衰退法和邻域标准差算法参与融合,这两种算法运算快速,且性能相对稳定。连续非极大值衰退法属于中心检测法,邻域标准差算法属于边界检测法,因此在算法本质上互不相同,互补性强。
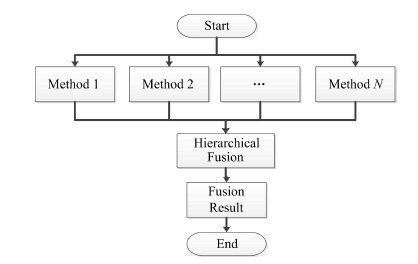
融合算法的另一个核心步骤是对探测结果置信度的计算。在本项目中,每个探测到的晶体都要计算一个置信度。传统信息融合往往通过简单的权值相加或概率加权的方法对结果做出判断,这种单层级的融合只能纳入一维的信息,而探测到的晶体信息包括位置,行编号和列编号等多维信息。为了更有效地进行信息融合,我们采用分级融合策略,将多个维度上信息一致的设为最高置信度,部分一致的设为第二级,完全不一致为第三级。根据置信度从高到低依次处理,并以置信度高的矫正结果,动态矫正置信度低的信息,这样可以为融合处理增加判断依据,提高算法的鲁棒性。多探子融合算法整体流程如图 2所示。
|
图 2 算法流程图 Fig.2 Algorithm technical scheme. |
连续非极大值衰退法[5]是一种典型的晶体中心检测法,其核心点为基于非极大值连续衰退的局部极大值探测、中心十字架递推预排序和基于行列样条拟合的晶体阵列排序矫正。该算法对晶体阵列形变有很好的自适应矫正能力,但是结果对图像预处理技术依赖性强。以局部直方图均衡和高斯差分这两种图像预处理方法为例,如图 3所示,(a)、(b)为原始二维位置直方图,(c)、(d)分别是对(a)、(b)进行高斯差分预处理后的结果,(e)、(f)分别是对(a)、(b)进行局部直方图均衡预处理后的结果。从图 3中椭圆标记的部分可以看出,局部直方图均衡能够有效分割黏连点,但是易受伪影影响;高斯差分的方法相对来说受伪影干扰小,但是容易造成低能量晶体点的漏检。由此可以看出,连续非极大值衰退法使用不同的预处理方法得到的结果有很强的互补性,所以在本项目中使用局部直方图均衡和高斯差分作为连续非极大值衰退法的两种图像预处理方法,并将预处理方法不同的探测方法视为两种独立的不同的探测方法参与后期的融合。

|
图 3 连续非极大值衰退法不同预处理方法对比 Fig.3 Effect of different pre-processing methods to successive non-maximum decay algorithm. |
邻域标准差算法[8]是一种晶体边界检测算法,它使用类似转动惯量的特征算子增强二维位置直方图中的峰谷比,得到邻域标准差图像(如图 4(b)、(c)所示)。随后,直接对邻域标准差图像在X和Y方向上逐行逐列寻峰,这些峰值就是晶体阵列行列的边界。由于实际结果中这些峰的位置并非完美相接,我们使用anisotropic diffusion方法[10]使线段尽可能相连接。该算法能克服噪声和灰度不均的影响,但是在晶体黏连严重的位置,无法在邻域标准差的图像上得到高亮的响应,而且在晶体阵列行列扭曲严重的时候,会造成行列边界线的错连(如图 4(c)、(d)的椭圆框所示)。

|
图 4 邻域标准差图像 Fig.4 Results of neighborhood standard deviation algorithm. |
晶体中心检测法和晶体行列检测法可参与融合的结果信息有:晶体中心点的位置,中心点的行、列编号;晶体边界检测法中参与融合的结果信息有:被边界所包围的晶体块的位置,晶体块的行、列编号。
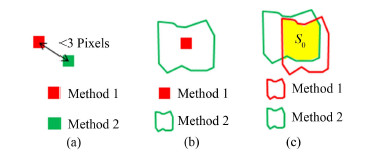
2.2.2 一致性判定对不同的探测方法的结果信息进行一致性判定以单个晶体为单位。结果信息中的单个晶体包含三个主要信息:位置信息和行、列编号。中心检测法,行列检测法与边界检测法的唯一不同在于位置信息,前两者得到的是晶体块中心点的位置,后者是晶体块边界所包含的位置。在本项目中,对不同探测结果的位置信息一致性的定义可分为以下几种(图 5):1)晶体块中心与晶体块中心的距离小于3个像素;2)晶体块边界包含且只包含一个晶体块的中心点;3)两个晶体块边界所包围的位置相交部分不小于相并部分的2/3,即$\frac{{{S_1} \cap {S_2}}}{{{S_1} \cup {S_2}}} \ge \frac{2}{3}$,其中S1、S2分别表示方法1和方法2的结果边界所包围位置的面积。而对于行、列编号的一致性则是指晶体被赋予的行、列索引信息相同。
|
图 5 不同方法的位置一致性判定 Fig.5 Position consistency judgment for algorithms of different kinds. |
基于上述一致性判定条件,在融合处理过程中,对不同晶体检测算法得到的晶体信息进行相似性量化分级,对同一晶体,不同结果之间得到的信息越相似,说明该结果的置信度越高。在本项目中我们将各晶体信息的置信度由高到低依次分为一级融合、二级融合和三级融合。
一级融合表示参与融合的不同结果中对同一个晶体的位置信息和行列信息都满足上述一致性判定条件。
二级融合表示不同探测方法的结果部分相似,具体来讲,即多种方法在相近的位置探测到了晶体,但对其行列编号判定结果不完全一样。按“不完全一样”的程度又可细分为:1)行(列)编号不同但列(行)编号相同,2)行列编号皆不同但与周边晶体同属一行(列),3)行列编号皆不同且与周边晶体不属于同一行(列)。如图 6所示,为更直观的展示晶体的行列信息,所以把各探测结果中的行列编号信息拆开到两张图中分别显示,其中黑色点表示不满足排序递推条件而被弃用的晶格点,其余相近的同颜色晶格表示同行或者同列点。

|
图 6 二级融合的三种置信度示例 Fig.6 Three types of level 2 confidence. |
第一列和第二列图像为基于局部直方图均衡的连续非极大值衰退算法的列和行标定结果,第三列和第四列图像为基于高斯差分的连续非极大值衰退算法的列和行标定结果。每一行分别对应上述1)、2)、3)三种情况。图 6椭圆框中标记的晶体为两种探测方法都在相近的位置探测到了的晶体。对第一行图像中标记的三个晶体,在两种探测方法的结果中,晶体的列编号相同,但行编号不同;第二行图像中标记的两个晶体,晶体行列编号都不相同,但是从图 6 b21中可以推测,这两个晶体是属于同一列的;第三行图像中标记的晶体,则是行列编号都不相同,且无法单从此晶体的结果信息推断该晶体到底是属于哪一行哪一列,唯一能够确定的是该位置存在一个晶体。二级融合的置信度低于一级融合,且在二级融合中,1)、2)、3)三种情况的置信度依次减小。
当待融合的方法对晶体的位置信息都无法达成一致,即并不是所有的算法都在此位置探测到了一个晶体,这种结果置信度最低,被列为三级融合。
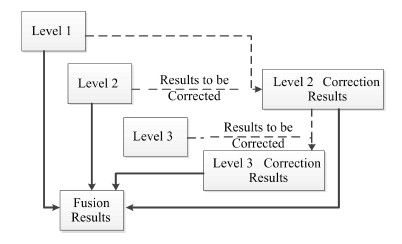
2.2.4 结果矫正对各探测结果完成相似性量化分级后,按照一级融合、高置信度二级融合、低置信度二级融合、三级融合的顺序对各晶体的结果信息依次进行结果矫正,从而得到最终的融合结果(图 7)。融合结果以晶体中心点的形式保留,对晶体边界检测算法,以晶体边界包围区域的质心为当前晶体中心点。
|
图 7 分层融合处理流程图 Fig.7 Scheme of hierarchical fusion method. |
一级融合的结果被所有结果所肯定,置信度最高,在融合结果中全部予以保留。
二级融合中晶体位置信息和在各个结果中相同的行或者列编号信息直接在融合结果中被采用,对于冲突的行或列编号信息,则按照相应的置信度高低,根据一级融合和已经处理的高置信度二级融合结果的行列样条拟合[11]结果信息确定。
三级融合的结果置信度最低,对该等级的晶格检测结果只保留相应晶格的位置信息,不保留行列编号。然后根据一级融合和二级融合矫正的结果,及晶体阵列的物理排布等先验知识,判断在此保留位置是否真的存在晶体。如果真的存在晶体,则根据行列样条拟合结果更新其行列编号信息,并将此晶体信息加入到融合结果中。
2.3 方法评价晶体检测结果正确与否以人工标定结果为金标准。整个测试数据集的准确率统计以整张二维位置直方图为单位,如果单张二维位置直方图中有任意晶体映射出现错误,则判定该二维位置直方图所代表的晶体阵列检测错误,准确率=检测正确的晶体阵列个数/该测试数据集中晶体阵列个数总和。
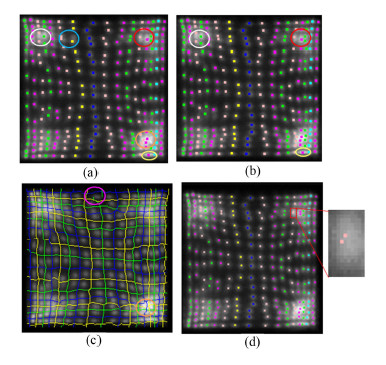
3 结果分析图 8前三张图是本项目中提到的基于局部直方图均衡的连续非极大值衰退法、基于高斯差分的连续非极大值衰退法和邻域标准差算法这三种探测算法对PET2中的一张二维位置直方图的处理结果,第四张是对前面三种算法结果按照多探子融合算法融合处理后得到的结果。从图 8中椭圆框出的位置可以看出,对该张二维位置直方图前三种算法的检测结果各有错误,而本项目提出的多探子融合算法综合参与融合的三种算法的探测结果,最后正确地探测和标记该二维位置直方图晶体阵列中的所有晶体。如图 8(a)和(b)中右侧椭圆框标记的位置,前两种方法均未正确标记晶格点,而邻域标准差算法准确地找到了晶格的边界位置,结合当前晶格及其周边已经被矫正的高置信度晶格的结果,多探子融合算法在将缺失的晶格中心点在对应的位置补上,图 8(d)中方框内的两个晶格点由于本身二维位置直方图上晶格发生黏连的原因,探测标记结果十分靠近,其对应位置的放大图和标记结果如右侧的小框图所示。
|
图 8 不同探测方法结果对同一个晶体阵列检测结果对比 Fig.8 Crystal identification results obtained with different algorithms. |
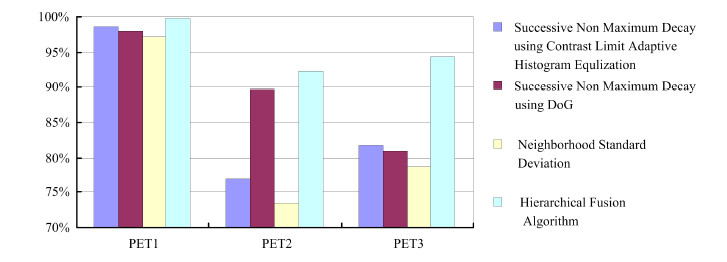
图 9是用包括本项目提出的多探子融合算法在内的4种方法,对三组PET数据中的所有二维位置直方图进行测试的结果对比,横轴表示不同的PET探测器得到的二维位置直方图测试数据集(PET1、PET2、PET3),纵轴表示晶体检测的准确率。不同颜色的柱状数据表示不同探测方法的结果。从图 9中可以看出,在图像质量最好的PET1数据集中,所有算法都达到95%以上的准确率,而多探子融合算法更是取得了99.8%的检测准确率,接近完全自动化水准。在晶体阵列整体形变严重,行列扭曲严重的PET2图像中,基于高斯差分的连续非极大值衰退法是前三种探测方法中表现最好的,多探子融合算法则在保持基于高斯差分的连续非极大值衰退算法结果的前提下,结合其余两种算法优势,使检测准确率有了进一步的提升。在低信噪比的PET3图像上,多探子融合算法最大程度的展示了它的优势,前三种探测算法的准确率均在80%左右,而多探子融合算法却获得了94.3%的准确率,性能提升非常明显。
|
图 9 不同检测算法晶体分割准确率对比 Fig.9 Crystal segmentation success rate of different algorithms. |
以上所有结果均在搭载Intel Core i5-4590处理器、主频3.3 GHz、内存12 GB、Windows 7系统的台式机上测试完成,开发环境为C++。在本实验环境下,对设备PET1、PET2和PET3中的所有晶体的探测分别耗时3.87 min、4.79 min和4.66 min。平均每张二维位置直方图中晶体探测耗时0.6 s左右。
4 结语实验结果表明,各探测方法对不同类型的二维位置直方图有其各自的适应性和局限性,本文提出的多探子融合算法利用各探测方法结果的互补性,自动矫正大部分的探测错误,提升晶体自动检测的准确率。经大量实验结果证明,在不同质量的PET探测器上多探子融合算法均能保证90%以上的晶体查找表无需人工干预,从而极大地降低人工检查和修正花费的时间。尤其在设备老化,二维位置直方图质量低劣时,对比单一探测方法的结果,多探子融合算法性能提升更为明显。
不同于简单的概率加权融合算法,该算法在矫正过程中以高置信度的晶格点矫正低置信度的晶格点,不仅考虑了当前晶格点的探测结果,也加入了周边晶格点的信息。当大多数的探测方法对某个晶格给出的结果一致性较弱时,也可根据周边一致性强晶格点推算出该晶格点的正确位置和行列信息。
多探子融合算法也有其局限性,某些过差的晶体探测结果将对融合过程中置信度分级判断和结果矫正造成干扰,导致最后的融合结果对有些二维位置直方图比参与融合的单一探测结果更差。但是,从整体实验结果来看,本项目提出的多探子融合算法在参与对比的参与融合的所有晶体检测方法中对每一组测试数据的表现都是最佳的。此外,由于多探子融合算法在实现时综合了多种算法的结果,耗时相对较长。在二维位置直方图像质量较好,信噪比较高,晶格阵列更规整,晶格峰谷比更高时,参与融合的某种算法就能获得相对比较好的结果,此时多探子融合算法的优势并不明显。
| 1 | 柴培,单保慈.正电子发射断层扫描仪Block探测器晶体位置表的建立[J].中国科学E辑:技术科学,2009,39(01):103-108 CHAI Pei,SHAN Baoci.The establishment of crystal position look-up table for positron emission tomography with block detectors[J].Science China E:Technological Sciences,2009,39(01):103-108( 1) 1) |
| 2 | 胡均松,邓明亮,王新增,等.基于LYSO正电子发射乳腺断层成像系统探测器的设计与评估[J].核技术,2013,36(10):100401.DOI:10.11889/j.0253-3219.2013.hjs.36.100401 HU Junsong,DENG Mingliang,WANG Xinzeng,et al.Design and evaluation of positron emission mammography based on LYSO[J].Nuclear Techniques,2013,36(10):100401.DOI:10.11889/j.0253-3219.2013.hjs.36.100401( 1) 1) |
| 3 | Stonger K A,Johnson M T.Optimal calibration of PET crystal position maps using Gaussian mixture models[J].IEEE Transactions on Nuclear Science,2004,51(1):85-90.DOI:10.1109/TNS.2004.823334( 1) 1) |
| 4 | Breuer J,Wienhard K.PCA-based algorithm for generation of crystal lookup tables for PET block detectors[J].IEEE Transactions on Nuclear Science,2009,56(3):602-607.DOI:10.1109/TNS.2009.2019587( 1) 1) |
| 5 | 上海联影医疗科技有限公司.晶体中心位置图生成方法及晶体像素查找表生成方法[P].CN104809460,2015-07-29 Shanghai United Imaging Healthcare Corporation.A method for establishing crystal center position map and crystal look-up table[P].CN104809460,2015-07-29( 2) 2) |
| 6 | 陈忻,陈源宝,牛明,等.PET探测器晶体位置快速在线辨识算法[J].中国科技论文,2013,8(04):282-286.DOI:10.3969/j.issn.2095-2783.2013.04.003 CHEN Xin,CHEN Yuanbao,NIU Ming,et al.Fast online crystal identification algorithm in positron emission tomography[J].China Science Paper,2013,8(04):282-286.DOI:10.3969/j.issn.2095-2783.2013.04.003( 1) 1) |
| 7 | Chaudhari A J,Joshi A A,Bowen S,et al.Crystal identification in positron emission tomography using nonrigid registration to a Fourier-based template[J].Physics in Medicine and Biology,2008,53(18):5011-5027.DOI:10.1088/0031-9155/53/18/011( 1) 1) |
| 8 | Wei Q Y,Li X D,Ma T Y,et al.A neighborhood standard deviation based algorithm for generating PET crystal position maps[C].Seoul:IEEE Press,2013:1-4.DOI:10.1109/NSSMIC.2013.6829273( 2) 2) |
| 9 | Du H,Burr K.An algorithm for automatic flood histogram segmentation for a PET detector[C].Anaheim:IEEE Press,2012:3488-3492.DOI:10.1109/NSSMIC.2012.6551796( 1) 1) |
| 10 | Weickert J,Romeny B M T H,Viergever M A.Efficient and reliable schemes for nonlinear diffusion filtering[J].IEEE Transactions on Image Processing,1998,7(3):396-410.DOI:10.1109/83.661190( 1) 1) |
| 11 | Hu Z H,Kao C M,Liu W,et al.Semi-automatic position calibration for a dual-head small animal PET scanner[C].Honolulu:IEEE Press,2007:1618-1621.DOI:10.1109/NSSMIC.2007.4437308( 1) 1) |


