GSI-191 (Generic Safety Issue-191)问题于1998年由美国核管会(United States Nuclear Regulatory Commission,U.S NRC)首先提出。该问题研究目的在于确定LOCA (Loss of Coolant Accident)事故之后,安全壳内碎片的传输和聚集是否会阻碍反应堆应急堆芯冷却系统(Emergency Core Cooling System,ECCS)的正常运行。对于压水堆的高能管道,即最高正常运行温度超过93.33 ℃或最高正常运行压力超过1.896 MPa的管道[1],当发生LOCA事故之后,破口附近的保温层和其他材料(如涂料和混凝土等)在喷射冲击作用下破裂成碎片。这些碎片将与安全壳内的常驻碎片和化学碎片一起迁移到地坑滤网并沉积形成碎片床。一部分碎片可能旁通地坑滤网并进入反应堆压力容器,引发一系列的效应。
为确定破口附近喷射冲击所产生的碎片量,本文基于ANSI/ANS 58.2-1988标准[2]和等效体积球体模型,自主开发了喷射冲击影响区域(Zone of Influence,ZOI)计算工具JETZOI,其中破口临界流的计算采用FORTRAN程序实现,其他部分的计算在EXCEL表格实现。本文首先针对压水堆主管道双端断裂事故,选取冷段滞止工况进行计算,并将计算结果与NEI (Nuclear Energy Institute)和NRC的结果进行对比验证,成功实现了ZOI计算方法的复现。进一步,本文进行了不同滞止工况的主管道双端断裂,包括冷段工况、热段工况和平均工况的敏感性分析计算。本文的工作可为喷射冲击试验的开展和GS1-191问题的研究解决提供有益借鉴。
1 ZOI计算模型概述当高能管道破裂时,破口喷出的流体能量足够高,可以在破口附近区域形成可迁移的碎片,该区域被定义为影响区域(ZOI)。ZOI主要用于在役电厂高能管线冲击所产生的碎片量的计算,也可用于指导新电厂安全壳内保温层、涂层和电缆等的布置。
ZOI的计算模型大致分为两类:圆锥模型和球体模型。当采用圆锥模型时,喷射冲击影响区域为沿破裂管道轴线的圆锥,假设破裂管道固定不动,喷射流体自由膨胀进入没有任何障碍的空间。圆锥模型包括ANSI/ANS 58.2-1988标准和三区圆锥喷射模型。然而,圆锥模型的自由膨胀无障碍射流只是一种理想假设。
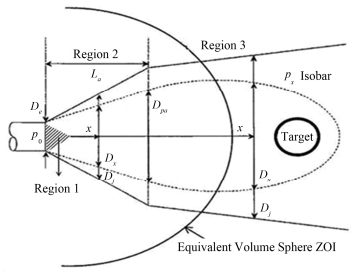
实际情况下,当管道发生破裂时,管道甩击移动,喷射流体可能在拥挤区域发生撞击反射。基于以上原因,球体模型对喷射冲击过程中出现的管道位移和射流反射进行包络,将ZOI考虑为以破口位置为球心的球体。球体模型包括三区球体模型和等效体积球体模型。其中等效体积球体模型建立在ANSI/ANS 58.2-1988标准的基础上,考虑了管道位移和射流反射效应,如图 1[3]所示。球体的ZOI半径(破坏半径)采用以下方式获得:
|
图 1 等效体积球体ZOI模型 Fig.1 Equivalent volume sphere model of ZOI. |
1) 通过喷射冲击试验测得所关心材料(保温层、涂料等)的破坏压力pdest。所谓破坏压力即材料在喷射冲击作用下开始破裂成碎片的阈值压力。
2) 采用ANSI/ANS 58.2-1988标准绘制喷射流体自由膨胀的轮廓及破坏压力pdest的等压线。即在图 1中,px=pdest。
3) 计算破坏压力pdest的等压线所包括的流体体积,并将其作为等效球体ZOI的体积。
4) 根据等效球体ZOI的体积计算球体ZOI的破坏半径。认为在以破口为球心,以破坏半径为半径的球体范围内,所关心的破坏压力为pdest的材料全部破裂为碎片。
2 ANSI/ANS 58.2-1988标准ANSI/ANS 58.2-1988标准[2]建立的目的在于为轻水堆核电厂假想管道破裂情况下出现的以下不利影响提供设计基础:管道甩击、管道内部载荷、喷射影响、隔间升压、环境工况和水淹,是已被NRC认可并被广泛应用的ZOI计算方法。
在ANSI/ANS 58.2-1988标准中,所采用的ZOI圆锥模型将喷射流体划分为三个区域:
1) 区域1:从破口平面到喷射核心(jet core)结束平面之间的区域。其中喷射核心为区域1内的小圆锥区域,内部压力假设为保持上游滞止压力。
2) 区域2:从喷射核心结束平面到渐近平面之间的区域。该区域为喷射流体继续等熵膨胀的区域。
3) 区域3:渐近平面之后的区域。该区域为喷射流体与环境作用膨胀的区域,喷射轮廓与喷射中心线的夹角为10°。
根据ANSI/ANS 58.2-1988标准,ZOI圆锥模型的计算方法详述如下。
2.1 冲击系数CT的确定当破口发生时,喷射流体产生冲击力,冲击力会在一段时间后达到稳定。
初始时刻的冲击力简化计算为破口面积乘以管道的初始滞止压力,即:
| ${T_{{\rm{INT}}}} = {p_0}A$ | (1) |
达到稳态的冲击力可写成以下形式:
| ${T_{{\rm{SS}}}} = {C_T}{p_0}A$ | (2) |
式中:CT为冲击系数,即稳态冲击力与初始冲击力的比值,由式(3)计算:
| ${C_T} = \left\{ \begin{array}{l} 2.0 - 0.861{h^{*2}} (0 \le {h^*} < 0.75)\\ 3.22 - 3.0{h^*} + 0.97{h^{*2}} (0.75 \le {h^*} \le 1.0) \end{array} \right.$ | (3) |
| ${h^*} = \frac{{{h_0} - 180}}{{{h_{\rm{f}}} - 180}}$ | (4) |
式中:h0为滞止焓;hf为滞止压力对应的饱和液焓。
2.2 临界质量流速Ge的确定临界质量流速Ge的计算,对于饱和或两相滞止工况,标准推荐采用HEM模型(Homogenous Equilibrium Model);对于过冷滞止工况,推荐采用Henry-Fauske模型。
当采用HEM模型时,临界质量流速Ge由式(5)计算:
| ${G_e} = {\left\{ {\frac{{\sqrt {2[{h_0} - (1 - {x_e}){h_{{\rm{f}}e}} - {x_e}{h_{{\rm{g}}e}}]} }}{{(1 - {x_e}){v_{{\rm{f}}e}} + {x_e}{v_{{\rm{g}}e}}}}} \right\}_{{\rm{out}}}}$ | (5) |
式中:h0为滞止焓;hf和hg分别为饱和液焓和饱和汽焓;vf和vg分别为饱和液比容和饱和汽比容;x为含汽率。各参数的下标e代表下游出口端参数。
当采用Henry-Fauske模型时,
| $\begin{array}{c} G_e^2 = \{ \frac{{{x_0}{v_{\rm{g}}}}}{{np}} + ({v_{\rm{g}}} - {v_{{\rm{f}}0}})[\frac{{(1 - {x_0})N}}{{{s_{{\rm{g}}e}} - {s_{{\rm{f}}e}}}}\frac{{d{s_{{\rm{f}}e}}}}{{dp}} - \\ _{}^{}\frac{{{x_0}{c_{p{\rm{g}}}}(\frac{1}{n} - \frac{1}{\gamma })}}{{p({s_{{\rm{g}}0}} - {s_{{\rm{f}}0}})}}]\} _t^{ - 1} \end{array}$ | (6) |
式中:下标t代表喉部参数;下标0代表上游滞止参数;sf和sg分别为饱和液熵和饱和汽熵;n为热力平衡多变指数;γ为等熵膨胀指数;N为衡量喉部与平衡过程偏离程度的量度。分别由以下公式计算获得:
| $n = \frac{{(1 - {x_0}){c_{v{\rm{f}}}}/{c_{p{\rm{g}}}} + 1}}{{(1 - {x_0}){c_{v{\rm{f}}}}/{c_{p{\rm{g}}}} + 1/\gamma }}$ | (7) |
| $\gamma = \frac{{{c_{p{\rm{g}}}}}}{{{c_{v{\rm{g}}}}}}$ | (8) |
| $N = \min [{({x_e})_t}/0.14,1]$ | (9) |
式中:cv和cp分别为定压比热和定容比热。
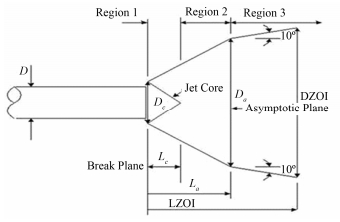
2.3 喷射轮廓的绘制前已述及,喷射流体包括三个区域,如图 2所示。以下分别介绍三个区域喷射轮廓的确定方法。
|
图 2 ANSI/ANS-58.2 1988标准圆锥ZOI模型 Fig.2 Conical ZOI model in ANSI/ANS-58.2 1988 standard. |
区域1包括喷射核心及喷射核心结束平面左侧的其他部分。其中喷射核心的长度Lc与上游滞止工况的过冷度有关,由式(10)计算:
| $\frac{{{L_c}}}{{{D_e}}} = 0.26\sqrt {\Delta {T_{{\rm{sub}}}}} + 0.5$ | (10) |
式中:De为破口直径。
喷射核心的直径Dc由式(11)计算:
| $\frac{{{D_c}}}{{{D_e}}} = \sqrt {C_{Te}^*} (1 - \frac{L}{{{L_c}}})$ | (11) |
式中:L为距离破口平面的水平长度。
| $C_{Te}^* = \left\{ \begin{array}{l} 2.0 (\Delta {T_{{\rm{sub}}}} > 0)\\ 1.26 (\Delta {T_{{\rm{sub}}}} = 0) \end{array} \right.$ | (12) |
区域1中除喷射核心之外的其他区域轮廓的确定方法与区域2一致,将在区域2介绍。
2.3.2 区域2区域2和区域3的交界面即渐进平面的面积Aa由式(13)确定:
| $\frac{{{A_a}}}{{{A_e}}} = \frac{{G_e^2}}{{{g_c}{\rho _{ma}}{C_T}{p_0}}}$ | (13) |
式中:Ge为破口平面处的质量流速,由§2.2的临界流模型确定;CT为§2.1确定的冲击系数;ρma为渐进平面处的密度,由渐进平面处的压力pa和上游滞止焓h0确定。其中,渐进平面处的压力pa由式(14)计算:
| $\frac{{{p_a}}}{{{p_{amb}}}} = 1 - 0.5(1 - \frac{{2{p_{amb}}}}{{{p_0}}})f({h_0})$ | (14) |
式中:pamb为安全壳环境的压力;p0为上游滞止压力;f (h0)为修正系数,由式(15)计算:
| $f({h_0}) = \left\{ \begin{array}{l} \sqrt {0.1 + \frac{{{h_0} - {h_{\rm{f}}}}}{{{h_{{\rm{fg}}}}}}} (\frac{{{h_0} - {h_{\rm{f}}}}}{{{h_{{\rm{fg}}}}}} > - 0.1)\\ 0 (\frac{{{h_0} - {h_{\rm{f}}}}}{{{h_{{\rm{fg}}}}}} < - 0.1) \end{array} \right.$ | (15) |
从破口平面到渐进平面的距离:
| $\frac{{{L_a}}}{{{D_e}}} = \frac{1}{2}(\sqrt {\frac{{{A_a}}}{{{A_e}}}} - 1)$ | (16) |
区域2的横截面积由式(17)确定,该公式同时适用于区域1中除喷射核心之外的其他区域以及区域2。
| $\frac{{{A_j}}}{{{A_{je}}}} = 1 + \frac{L}{{{L_a}}}(\frac{{{A_a}}}{{{A_{je}}}} - 1)$ | (17) |
式中:Aje为破口平面的射流面积。
| ${A_{je}} = {A_e}C_{Te}^*$ | (18) |
区域3的外轮廓与喷射中心线保持10°的夹角。其射流面积由式(19)确定:
| $\frac{{{A_j}}}{{{A_a}}} = {[1 + \frac{{2(L - {L_a})}}{{{D_a}}}\tan 10^\circ]^2}$ | (19) |
喷射流体三个区域的压力场的分布根据以下的方法确定。
2.4.1 区域1区域1内喷射核心的压力假设保持为上游滞止压力,其他区域的压力根据判别式确定。若$D_j^2 + 2D_j^{}D_c^{} + 3D_c^2 \le 6{C_T}$,则射流压力pj由式(20)计算:
| $\begin{array}{l} {p_j} = \frac{{{D_j} - 2r}}{{{D_j} - {D_c}}}[1 - \frac{{2(D_j^2 + D_j^{}D_c^{} + D_c^2 - 3{C_T})}}{{D_j^2 - D_c^2}}\\ (\frac{{2r - {D_c}}}{{{D_j} - {D_c}}})]{p_0} \end{array}$ | (20) |
需要注意的是,当位置接近射流外轮廓时,射流压力接近环境压力,而Dj-2r归零。因此,公式中的压力应代入表压。若$D_j^2 + 2D_j^{}D_c^{} + 3D_c^2 > 6{C_T}$,则:
| ${p_j} = {(\frac{{{D_j} - 2r}}{{{D_j} - {D_c}}})^2}[\frac{{6({C_T} - D_c^2)}}{{({D_j} - {D_c})({D_j} + 3{D_c})}}]{p_0}$ | (21) |
区域2的压力与射流中心线的压力pjc相关联。
| ${p_{jc}} = [{F_c} - ({F_c} - \frac{{3{C_T}}}{{D_a^2}})\frac{{{L_a}}}{L}\frac{{L - {L_c}}}{{{L_a} - {L_c}}}]{p_0}$ | (22) |
| ${p_j} = (1 - \frac{{2r}}{{{D_j}}})[1 - 2(\frac{{2r}}{{{D_j}}})(1 - \frac{{3{C_T}}}{{D_j^2}}\frac{{{p_0}}}{{{p_{jc}}}})]{p_{jc}}$ | (23) |
式(22)中:Fc为修正系数,由式(24)确定:
| ${F_c} = \min (1.0,6{C_T}/D_j^2)$ | (24) |
式中:Dj取L=Lc处的参数。
2.4.3 区域3区域3的压力同样与射流中心线的压力pjc相关联。
| ${p_{jc}} = \frac{{3{C_T}{p_0}}}{{D_a^2{{[1 + \frac{{2(L - {L_a})}}{{D_a^{}}}\tan 10^\circ]}^2}}}$ | (25) |
| ${p_j}{\rm{ = (}}\frac{{{D_j} - 2r}}{{{D_j}}}{\rm{)}}{p_{jc}}$ | (26) |
喷射流体三个区域的压力方程,即区域1的式(20)和(21)、区域2的式(23)以及区域3的式(26)可以写成以下通用的一元二次方程的形式,该方程即为等压线的特征方程:
| $A{r^2} + Br + C = 0$ | (27) |
式中的pj代入所关心材料的破坏压力pdest,给定距离L,求解方程即可获得与之对应的喷射流体轮廓半径r。将射流区域压力相同的点连接到一起,即获得破坏压力pdest的等压线。
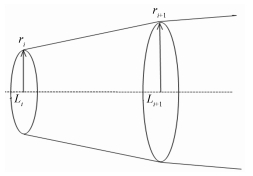
3 等效体积球体模型 3.1 等压线包络体积的计算根据ANSI/ANS 58.2 1988标准绘制的破坏压力pdest的等压线,进一步计算该等压线所包络的流体体积。取Li到Li+1之间的圆锥微元,如图 3所示。
|
图 3 用于体积计算的圆锥微元 Fig.3 Small conical element for volume calculation. |
其体积采用式(28)计算:
| $\begin{array}{c} {V_i} = {\rm{\pi }}[\frac{1}{3}m_i^2{L^3} + m_i^{}({r_{i + 1}} - {m_i}{L_{i + 1}}){L^2} + \\ _{}^{}(m_i^2L_{i + 1}^2 - 2{r_{i + 1}}{m_i}{L_{i + 1}} + r_{i + 1}^2)L] \end{array}$ | (28) |
式中:mi为圆锥的斜率,由式(29)计算:
| $m_i^{} = \frac{{{r_{i + 1}} - {r_i}}}{{{L_{i + 1}} - {L_i}}}$ | (29) |
将等压线所包络的流体区域沿射流方向离散,并将各圆锥微元的体积依次相加,即可获得等压线所包括的流体体积。对于双端断裂LOCA事故,需要将计算出的体积乘以2。即认为双端断裂的两段管道喷出的流体不发生相互影响而各自保持自由射流状态,这将使计算出的ZOI破坏半径和产生的碎片量保守最大。
3.2 ZOI破坏半径的确定根据ZOI计算模型中的等效体积球体模型,将§3.1计算获得的等压线包络体积等效为一球体的体积。该球体球心位于破口位置,半径由式(30)计算:
| ${R_{{\rm{dest}}}} = {(\frac{3}{{4{\rm{\pi }}}}{V_{{\rm{isobar}}}})^{1/3}}$ | (30) |
该半径即为ZOI的破坏半径,对于破坏压力为pdest的材料,在以破口位置为球心,以破坏半径Rdest为半径的球体内的该类材料将全部破裂成碎片。
4 计算结果分析 4.1 ZOI计算方法的复现在文献[4]的附录D中,NEI针对压水堆主管道双端断裂事故进行了计算。与破裂型破口相比,双端断裂型破口将导致碎片产生量最大。主管道滞止工况取冷段工况,即压力15.5 MPa,温度282.2 ℃,安全壳压力取0.101 MPa。并绘制了0.069 MPa的等压线。根据文献[4],0.069 MPa为三种保温层材料(包括无护套Nukon、带标准绑带的护套Nukon和Knaupf)的破坏压力。因此选取该压力绘制等压线具有典型意义。
在文献[5]的附录I中,NRC对参考文献[4]附录D的结果进行了审查和独立计算。认为其在区域2的计算上存在问题。该问题对喷射压力低于0.138MPa工况的影响可以忽略,而对较高喷射压力的工况影响较大。为此,NRC进行了15.5 MPa、276.7 ℃工况的独立计算,并重新绘制了0.069 MPa的等压线。
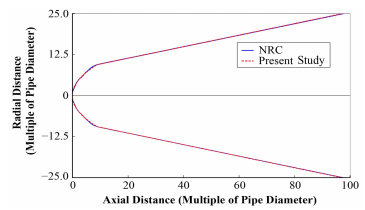
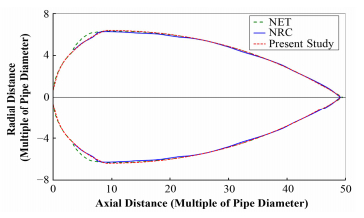
本文选取与NRC相同的工况进行计算,并将计算结果与NEI[4]和NRC[5]的结果进行对比。图 4给出了本文计算结果与NRC计算结果喷射轮廓的对比。由对比可以看出,两者基本重合。图 5给出了NEI、NRC和本文计算获得的0.069 MPa等压线的对比,本文结果与NRC结果可以很好吻合,而NEI结果由于在区域2的结果上存在问题,与本文结果和NRC结果出现明显的差别。本文采用等效体积球体模型对ZOI破坏半径进行了计算,并将其与NEI和NRC计算获得的ZOI破坏半径进行了对比,如表 1所示。由表 1可以看出,本文计算获得的破坏半径与NRC结果基本吻合,成功实现了对ZOI计算方法的复现。
|
图 4 喷射轮廓的对比 Fig.4 Comparison of jet outline. |
|
图 5 0.069 MPa等压线的对比 Fig.5 Comparison of 0.069 MPa isobar. |
| 表 1 ZOI破坏半径的对比 Table 1 Comparison of destruction radius of ZOI. |
本文采用开发的喷射冲击影响区域计算工具JETZOI,进行了不同滞止工况的敏感性分析。共计算了三类主管道双端断裂工况:冷段工况(15.5 MPa、276.7 ℃)、热段工况(15.5 MPa、332.2 ℃)和平均工况(15.5 MPa、304.4 ℃)。三类工况计算获得的冲击系数CT和临界质量流速Ge的对比如表 2所示。在相同的压力下,流体温度的升高将导致冲击系数CT和临界质量流速Ge的减小。前已述及,冲击系数CT表征了稳态冲击力与初始冲击力的比值。冲击系数的减小代表了稳态冲击力的降低,由此可定性判断喷射冲击对材料破坏效果的减弱。
| 表 2 敏感性分析结果对比 Table 2 Result comparison of sensitivity analysis. |
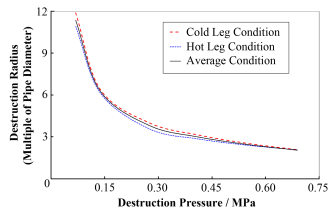
对于每一类工况,论文选取了一组破坏压力进行了敏感性分析,包括0.069 MPa、0.138 MPa、0.276MPa、0.414 MPa、0.552 MPa和0.689 MPa,并将三类工况计算获得的ZOI破坏半径Rdest进行了对比,如图 6所示。在三类工况中,冷段工况的破坏半径最大,随流体温度的上升,过冷度的下降,喷射冲击的破坏半径逐渐减小。该变化趋势是合理的,因为破坏半径体现了流体对材料的破坏效果。流体过冷度越低(流体温度越高),冲击系数CT越小,稳态冲击力也越小,流体的破坏效果越弱。因此,基于以上敏感性分析,为获得喷射冲击产生的碎片量,在开展喷射冲击试验获得ZOI的破坏半径时,应当保守选取冷段双端断裂工况作为极限工况以使喷射冲击产生的碎片量最大。
|
图 6 敏感性分析破坏半径的对比 Fig.6 Comparison of destruction radius for sensitivity analysis. |
本文针对GSI-191问题破口附近产生的碎片量,基于ANSI/ANS 58.2-1988标准和等效体积球体模型,自主开发喷射冲击影响区域计算工具JETZOI。采用JETZOI成功进行了ZOI计算方法的复现。进一步采用JETZOI进行了不同滞止工况的敏感性分析。分析结果表明,在相同的滞止压力下,流体温度的升高将导致冲击系数CT和临界质量流速Ge的减小,同时导致ZOI破坏半径的减小和碎片量的减少。因此在开展喷射冲击试验获得ZOI的破坏半径时,应当保守选取冷段双端断裂工况作为极限工况以使喷射冲击产生的碎片量最大。
| 1 | 李焕荣, 王鹏, 李达然, 等. AP1000 核电站常规岛高能管道断裂分析[J]. 电力建设, 2011, 32(3):88-91. DOI:10.3969/j.issn.1000-7229.2011.03.020 LI Huanrong, WANG Peng, LI Daran, et al. Analysis on high-energy pipe rupture in conventional island of AP1000 nuclear power plant[J]. Electric Power Construction, 2011, 32(3):88-91. DOI:10.3969/j.issn. 1000-7229.2011.03.020( 1) 1) |
| 2 | American Nuclear Society (ANS). American national standard design basis for protection of light water nuclear power plants against the effects of postulated pipe rupture[S]. ANSI/ANS 58.2-1988, 1988( 2) 2) |
| 3 | Knowledge base for the effect of debris on pressurized water reactor emergency core cooling sump performance[R]. NUREG/CR-6808, Los Alamos National Laboratory, 2003( 1) 1) |
| 4 | Nuclear Energy Institute (NEI). Pressurized water reactor sump performance evaluation methodology[R]. NEI 04-07, Vol.1, Rev.0, 2004( 4) 4) |
| 5 | U.S. NRC. Safety evaluation by the office of nuclear reactor regulation related to NRC generic letter 2004-02[R]. NEI 04-07, Vol.2, Rev.0, 2004( 2) 2) |
