2. 中国科学院等离子体物理研究所 合肥 230031;
3. 中国科学院合肥大科学中心 合肥 230031;
4. 中国科学技术大学 核科学技术学院 合肥 230026;
5. 首尔大学 核工程系 韩国首尔 151-742;
6. 核工业西南物理研究院 成都 610041
2. Institute of Plasma Physics, Chinese Academy of Sciences, Hefei 230031, China;
3. Hefei Science Center, Chinese Academy of Sciences, Hefei 230031, China;
4. School of Nuclear Science and Technology, University of Science and Technology of China, Hefei 230026, China;
5. Department of Nuclear Engineering, Seoul National University, Seoul 151-742, Korea;
6. Southwestern Institute of Physics, Chengdu 610041, China
在托卡马克等离子体中,杂质主要来源于等离子体与第一壁的相互作用。杂质的种类、含量以及输运过程对等离子体的品质有着重要的影响,例如改变等离子体的参数分布、降低约束性能、引起高约束模向低约束模的转变、激发磁流体不稳定性等现象[1]。对杂质的产生及输运行为的研究,对于控制杂质的聚芯、提高等离子体的性能有重要的意义,而首先就需要获得杂质的种类和含量信息。在高温等离子体条件下,杂质辐射覆盖波段非常宽广,从硬X射线直至近红外、远红外波段[2, 3, 4, 5]。被动光谱诊断主要是利用杂质粒子的线辐射谱或连续辐射谱进行测量,实现杂质种类与含量的实时监测。
本文描叙了基于被动光谱诊断测量杂质密度分布的方法。由空间多道摄谱仪被动测量获得杂质辐射的弦积分相对强度分布,通过谱仪强度标定系数转换得到绝对光亮度分布,基于测量弦的空间分布及等离子体位形,进一步反演变换获得杂质辐射的局部体发射率。获得体发射系数后,就可以根据相关原子数据库求得杂质电离态的离子密度。大部分情况下,我们只能观测到该杂质的单个或两三个电离态的分布剖面。借助杂质输运模拟程序模拟观测到的电离态密度分布剖面,可以获得该杂质所有电离态的分布剖面,最终获得该杂质在等离子体中的相对含量。本文以东方超环(Experimental Advanced Superconducting Tokamak,EAST)托卡马克装置上软X射线及极紫外光谱(Soft X-ray and Extreme Ultraviolet Spectrometers,XEUV)诊断测量到的Mo XXX(波长为12.242 nm)、Mo XXXI(波长为11.5988 nm)和Mo XXXII(波长为12.7868 nm)为例,计算获得了Mo杂质的密度分布。
1 光谱法测量杂质密度 1.1 杂质线辐射光谱的弦积分测量依据等离子体放电参数的不同,杂质辐射的主要波段也不相同。在边界等离子体区域,等离子体的温度密度较低,杂质电离态也较低,辐射波段主要集中在真空紫外和可见光波段。常见的杂质电离态为CII-III、O I-O V、Fe I、Mo I、W I等[6],对应的光谱诊断系统有可见及近紫外转镜扫描系统、光学多道分析仪等。芯部等离子体温度密度较高,在1keV量级,杂质线辐射主要集中在软X射线及极紫外波段。该波段涵盖了许多杂质高电离态的辐射共振线,低Z杂质如C、O、B的类氢、类氦线,高Z杂质如Fe、Cr、Ni、Cu、Mo的类锂、类氖线。对应的光谱诊断系统为软X射线-极紫外光谱诊断(Soft X-ray and Extreme Ultraviolet Spectrometers,XEUV)。
要获得杂质的含量,必须对相应的光谱诊断进行强度标定。在可见光波段,可以采用绝对标定过的积分球作为标准光源对系统进行标定,由于不涉及真空部件,标定相对比较简单。对于真空紫外和极紫外光谱仪,由于光源稀缺,强度标定工作比较困难。目前主要的标定方法有同步辐射光源标定[7]、线辐射分支比法[8]。轫致辐射谱法[9, 10]是近年来发展起来的适用于托卡马克装置的原位标定法,通过谱仪直接测量的轫致辐射强度与可见光轫致辐射诊断获得的结果外推至真空紫外波段,得出谱仪的强度标定系数。该方法既克服了同步辐射谱法需要来回移动光谱仪的不便,又克服了分支比法杂质谱线对数目少、强度弱的缺点,可以实现更精确的原位标定。
轫致辐射是指在电子和离子碰撞过程中,电子在库伦场中加速或减速时产生的辐射,其辐射功率的计算公式为[10]:
| ${U_{brem}} = 1.9 \times {10^{ - 28}}\frac{{n_e^2Z_{eff}^2{g_{ff}}}}{{{\lambda ^2}T_e^{1/2}}}exp\left( {\frac{{ - {{12}^{}}395}}{{\lambda {T_e}}}} \right)$ | (1) |
式中:ne是等离子体电子密度,cm-3;Te是等离子体电子温度,eV;Zeff是有效电荷数;gff是岗特因子;λ是相关位置的波长,nm。电子密度和电子温度可以有汤姆逊散射诊断[11]获得,而有效电荷数可以由可见轫致辐射测量[12]得到。将式(1)沿观测弦积分,即可得到弦积分的辐射功率Pbre。轫致辐射是连续谱,在选定光谱波段做强度标定时就需要避开线辐射谱线存在的区域。通过对比轫致辐射光子数和电荷耦合元件(Charge-coupled Device,CCD)观察到在相应波段的轫致辐射计数,就可以获得标定系数。图 1为EAST上EUV光谱仪采用轫致辐射谱法所获得的标定系数跟波长的关系曲线。
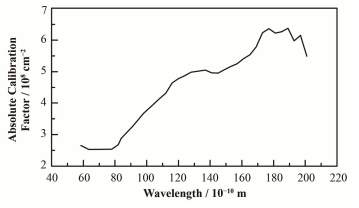
|
图 1 EAST装置EUV所选波段中心波长强度标定结果 Fig.1 Sensitivity calibration coefficients as a function of wavelength of EUV system on EAST. |
等离子体诊断中的被动光谱测量均为弦积分测量,在完成强度标定之后,将线辐射谱线剖面通过绝对标定系数转换即获得谱线的绝对光亮度分布。
1.2 反演变换获得体发射率由于谱线的绝对光亮度是基于光谱诊断测量的弦积分分布,需要对其进行反演,才能获得杂质在空间磁面点的局部信息。国际上比较常用的反演方法是阿贝尔反演[13]。由光谱仪观测到的弦积分光亮度和局部体发射率的关系为[13]:
| $B({r_i}) = 2\int_{{r_i}}^{{r_{\max }}} {\frac{{E(r)}}{{\sqrt {{r^2} - r_i^2} }}} dr$ | (2) |
式中:B为弦积分测量的光亮度;E为局部体发射系数,这里认为在一定的磁面区域内是定值,且只与径向距离r有关;i为观测弦道数编号。根据数学上的阿贝尔逆变换,可得:
| $E({r_j}) = \frac{1}{\pi }\int_{{r_i}}^{{r_{\max }}} {dr\frac{{dB(r)}}{{dr}}} \frac{{dr}}{{\sqrt {{r^2} - r_i^2} }}$ | (3) |
式中:j为等离子体磁面间区域编号。数值求解时,积分可以采用离散化处理,则光亮度和体发射率的关系可以写成[14]:
| ${B_i} = \sum\limits_j {{L_{ij}}{E_j}} $ | (4) |
| ${E_j} = \sum\limits_i {L_{ij}^{ - 1}{B_j}} $ | (5) |
式中:Lij为第i条观测弦在第j个磁面区域内的长度矩阵;$L_{ij}^{ - 1}$为其逆矩阵。对于圆截面位形,如图 2所示,其值可以写成:
| ${L_{ij}} = \left\{ \begin{array}{l} 2\sqrt {p_j^2 - r_i^2} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;({p_j} > {r_i},i = j)\\ 2(\sqrt {p_j^2 - r_i^2} - \sqrt {p_{j - 1}^2 - r_i^2} \;\;\;({p_j} > {r_i},i \ne j)\\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;({p_j} > r) \end{array} \right.$ | (6) |
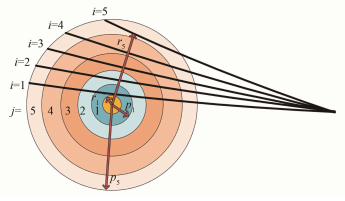
|
图 2 圆截面位形阿贝尔反演示意图 Fig.2 Abel inversion diagram of circular cross section. |
对于偏滤器拉长位形,等离子体放电位形大部分情况下都不是圆位形,这里每个圆都没有固定的半径。因此长度矩阵Lij的求法与在圆位形下会有所不同。这里可以将长度矩阵划分为强场区长度矩阵和弱场区长度矩阵。具体方法是:我们先从数据库中读取磁面信息,挑选出与每条观测弦相切的磁面。然后依次找出每一条弦和其它圆相交的交点,如图 3所示。
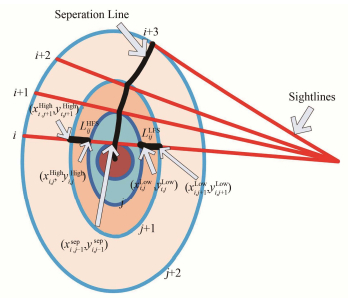
|
图 3 非圆截面阿贝尔反演示意图 Fig.3 Abel inversion diagram of non-circular cross section. |
观测弦用i、i+1、i+2等表示,相切圆分别用j、j+1、j+2等表示。每个交点的位置利用(x,y)坐标表示,则可以用两点间距离及距离差来表示长度矩阵。即:
| ${L_{ij}} = \left\{ \begin{array}{l} \sqrt {{{(x_{i,j}^{High} - x_{i,j - 1}^{High})}^2} + {{(y_{i,j}^{High} - y_{i,j - 1}^{High})}^2}} + \\ \;\sqrt {{{(x_{i,j}^{Low} - x_{i,j - 1}^{Low})}^2} + {{(y_{i,j}^{Low} - y_{i,j - 1}^{Low})}^2}} \;\;\;{\;^{}}(i < j)\\ \sqrt {{{(x_{i,j}^{High} - x_{i,j}^{Low})}^2} + {{(y_{i,j}^{High} - y_{i,j}^{Low})}^2}} \;\;\;\;{\;^{}}(i = j)\\ 0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;(i > j) \end{array} \right.$ | (7) |
以波长为12.242 nm的 Mo29+谱线为例,其体发射系数可以写成[14]:
| $\begin{array}{l} E_{Mo}^{12.242} = {n_{M{o^{29 + }}}}(\rho ) \cdot {n_e}(\rho ) \cdot PE{C^{exc}}(\rho ) + \\ \;\;\;\;\;\;\;\;\;\;\;{n_{M{o^{30 + }}}}(\rho ) \cdot {n_e}(\rho ) \cdot PE{C^{rec}}(\rho ) + \\ \;\;\;\;\;\;\;\;\;\;\;{n_{M{o^{3{\rm{0}} + }}}}(\rho ) \cdot {n_e}(\rho ) \cdot PE{C^{CX}}(\rho ) \end{array}$ | (8) |
式中:n代表杂质离子或等离子体电子密度;PECexc(ρ)、PECrec(ρ)和PECCX(ρ) (ρ为磁面坐标)分别是激发辐射、复合辐射以及电荷复合交换光子发射系数[12, 13]。对于芯部等离子体来说,在没有中性束注入的情况下,电荷交换复合的贡献可以忽略。当考虑杂质电离态存在于等离子体的稳态过程,复合辐射的贡献也可以忽略[14]。通过ADAS (Atomic Data and Analysis Structure)数据库获得激发辐射光子发射系数,输入杂质电离态特定波长以及对应位置的电子温度和密度,即可读取对应辐射光子系数。这样,杂质离子密度可以由式(8)反推得出:
| ${n_{M{o^{29 + }}}}(\rho ) = E_{M{o^{29 + }}}^{12.242}{\rm{ }}({n_e}(\rho ) \cdot PEC_{12.242}^{exc}(\rho ))$ | (9) |
使用同样的方法,就可以计算杂质其它电离态离子的密度。
1.4 基于杂质输运计算杂质总密度分布一般很难直接测到一种杂质所有电离态密度的分布,大部分情况下,单次只能测到该杂质的一条或几条电离态剖面分布。这时可以借助杂质输运模拟运算得出该杂质所有电离态的分布。杂质输运方程为[15, 16]:
| $\frac{{\partial {n_Z}}}{{\partial t}} = - \frac{{\rm{1}}}{r}\frac{\partial }{{\partial r}}(r{\Gamma _Z}) + {Q_Z}$ | (10) |
式中:${n_Z}$是电离态为Z的杂质离子密度;${\Gamma _Z}$是电离态为Z的杂质离子通量;QZ是电离态为Z的离子密度净增益,包括离子密度的源和漏两项,包括由于电离、复合以及电荷交换等带来的离子密度的增加和减少,这些项将相邻的电荷态离子密度联系起来。在仅考虑相邻的电离态的直柱一维近似处理中,杂质输运方程为[17]:
| $\frac{{\partial {n_Z}}}{{\partial t}} = \frac{{\rm{1}}}{r}\frac{\partial }{{\partial r}}r(D\frac{{\partial {n_Z}}}{{\partial r}} - v{n_Z}) + {Q_Z}$ | (11) |
式中:D是杂质扩散速度;v是杂质对流速度,其数值的正负分别表示向外和向内的对流。杂质离子密度净增益为:
| $\begin{array}{l} {Q_Z} = - \left( {{n_e}{S_Z} + {n_e}{\alpha _Z} + {n_H}{C_Z}} \right){n_Z} + {n_e}{S_{Z - 1}}{n_{Z - 1}} + \\ \;\;\;\;\;\left( {{n_e}{S_{Z + 1}} + {n_e}{\alpha _{Z + 1}} + {n_H}{C_{Z + 1}}} \right){n_{Z + 1}} \end{array}$ | (12) |
式中:SZ、αZ和CZ分别是电离态为Z的杂质离子电离系数、复合系数(辐射复合和双电子复合)和电荷复合交换系数。
输运方程式(10)中,对于同一杂质不同离子电离态的求解通常需要运用数值方法进行,一般都采用数值模拟代码来完成计算。目前国际上常用的几个杂质输运代码有STRAHL (Stand-alone Impurity Transport Code)、MIST (Multi-Ionic Species Transport)、ZIMPUR (High-Z Impurity Code)、TOTAL (Toroidal Transport Analysis Linkage)、SANCO (Stand-Alone Non-Corona)[18]等。这些程序运行时需要提供一些基本参数,包括基本参数(即电子密度剖面和电子温度剖面)、等离子体几何位形、预设扩散对流系数、原子数据(杂质电离系数、复合系数、光子辐射跃迁系数等),这些原子数据主要通过查找ADAS数据库来获得。对于电荷复合交换过程,还需要提供中性粒子密度。通过输入杂质输运系数,对输出杂质剖面结果和实验测量的几个相邻杂质电离态剖面进行对比,通过最优化方法找出适当的扩散系数和对流系数,并得出所有杂质所有电离态的密度分布。
2 杂质密度测量实例EAST装置是世界上第一个具有非圆截面的全超导托卡马克,具有稳态运行的能力,可以开展长脉冲运行和稳态高约束模式(H-模)研究。2012年的EAST实验中,第一壁为金属钼材料,偏滤器用的是石墨,而真空室和射频波发射天线中使用了大量的不锈钢等金属材料。EAST的实验观测中,最常见的杂质是C、O、Li[4];金属杂质有Mo、Fe、Cr、Ni、Cu[18]。经过几年的持续发展,EAST装置上已成功和正在发展的诊断系统超过30多项。对于杂质密度测量,主要有XEUV光谱仪、二维弯晶谱 仪[19, 20]、边界被动光谱诊断(Edge Rotation Diagnostics,ERD)、多道线辐射阵列测量、单道多条线辐射监测等几套常规诊断。对于芯部的Mo杂质线辐射测量,主要使用XEUV光谱仪。
我们用的谱线是波长为12.242 nm的Mo XXX (3s3p2 2D3/2→3s23p 2P1/2)、波长为 11.598 8 nm的Mo XXXI (3s3d 3D2→3s3p 3P2)和波长为12.7868nm的Mo XXXII (2p63p 2P3/2→2p63s 2S1/2)。H-模放电中测得的弦积分线辐射分布如图 4所示,经过强度标定转换获得光亮度分布,之后采用非圆截面阿贝尔反演方法对钼杂质谱线亮度进行阿贝尔反演处理,即可反演获得钼杂质线辐射谱线的强度分布(即体发射系数),如图 5(a)所示。得到体发射系数之后,可根据式(9)计算Mo29+(Mo30+和Mo31+类同)离子的密度,用到的电子温度和密度剖面来源于汤姆逊散射诊断[11],计算结果如图 5(b)所示。
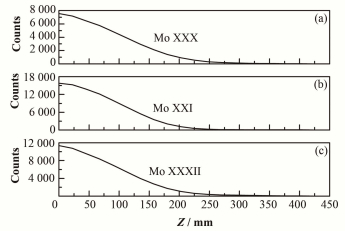
|
图 4 EAST装置H-模放电的钼杂质线辐射剖面 Fig.4 Intensity profiles of molybdenum ions during H-mode on EAST. |
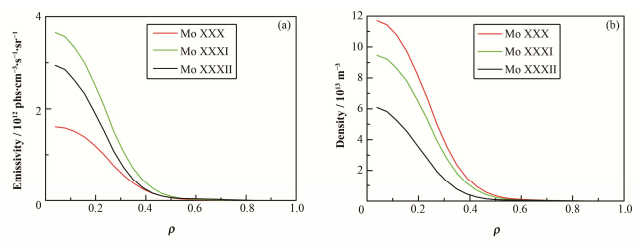
|
图 5 EAST装置H-模放电的钼杂质体发射率(a)和离子密度(b)剖面 Fig.5 Emissivity (a) and density (b) profiles of molybdenum ions during H-mode on EAST. |
得到Mo29+、Mo30+以及Mo31+的密度之后,就可以结合杂质输运程序对钼的输运系数进行模拟计算进而得到钼杂质的总密度。式(10)提到的输运方程,稳态情况下,获得三个杂质相邻三个电离态的密度剖面,即可对该杂质的输运系数进行模拟。将磁面信息、电子密度和温度信息生成相关的几何及等离子体参数文件输运程序代码,提供钼杂质的相关原子数据信息,然后通过输入扩散系数D和对流系数v即可进行模拟计算。对于杂质离子的密度剖面,其峰值位置和轮廓对杂质离子输运系数比较敏感,且主要由杂质粒子输运系数决定。通过不断变化D和v,即可改变模拟的钼杂质粒子剖面形状,模拟最终得到的密度剖面和实验剖面区域一致。同时得到芯部主要电离态的密度剖面和钼杂质总密度剖面分布,如图 6所示,剖面呈现一定的峰化趋势,钼的芯部总杂质密度比电子密度低5个量级。
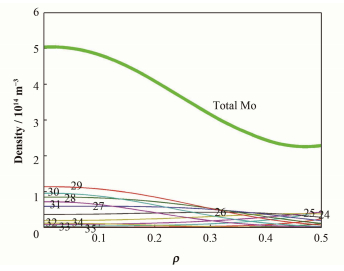
|
图 6 EAST装置H-模放电的芯部钼杂质密度剖面 Fig.6 Total density profiles of molybdenum during H-mode on EAST. |
该计算过程的误差主要来源于电子温度测量、电子密度测量带来的不确定性,而由XEUV谱仪测量的杂质剖面误差可以忽略不计。经测算,总误差小于10%。
3 结语本文主要介绍基于被动光谱诊断测量杂质密度分布方法。被动光谱诊断测量获得杂质线辐射的弦积分相对强度分布,通过光谱诊断强度标定系数转换得到绝对光亮度分布,进一步通过反演变换即可得到杂质谱线局部体发射率。根据体发射率和杂质离子密度关系,通过查找相关原子数据库数据可以求得杂质电离态的离子密度。根据测量的一条或几条电离态剖面分布,借助于杂质输运模拟运算得出该杂质所有电离态的分布。最后,给出了测量杂质密度分布方法实例,基于EAST装置托卡马克上软X射线及极紫外光谱诊断测量到的Mo XXIX-Mo XXXII获得Mo杂质的密度分布。杂质密度测量是进行杂质辐射计算和杂质输运研究的前提,对托卡马克等离子体物理研究起着重要的作用。
| 1 | Isler R C. Impurities in tokamak[J]. Nuclear Fusion, 1984, 24(12):1599-1678. DOI:10.1088/0029-5515/24/12/008( 1) 1) |
| 2 | Shen Y C, Du X W, Zhang W, et al. Space-resolved extreme ultraviolet spectrometer system for impurity behavior research on experimental advanced superconducting tokamak[J]. Nuclear Instruments and Methods in Physics Research Section A, 2013, 700(1):86-90. DOI:10.1016/j.nima.2012.10.070( 1) 1) |
| 3 | Shen Y C, Lu B, Du X W, et al. Spatially-resolved flat-field soft X-ray spectrometer on Experimental Advanced Superconducting Tokamak[J]. Fusion Engineering and Design, 2013, 88(11):3072-3077. DOI:10.1016/j.fusengdes.2013.08.003( 1) 1) |
| 4 | Shen Y C, Lyu B, Du X W, et al. Impurity emission behavior in the soft X-ray and extreme ultraviolet range on EAST[J]. Plasma Science and Technology, 2015, 17(3):183-187. DOI:10.1088/1009-0630/17/3/02( 1) 1) |
| 5 | Fu J, Li Y Y, Shi Y J, et al. Spectroscopic measurements of impurity spectra on the EAST tokamak[J]. Plasma Science and Technology, 2012, 14(12):1048-1053( 1) 1) |
| 6 | 周倩. HT-7 托卡马克等离子体基本杂质行为及杂质粒子输运分析[D]. 合肥:中国科学院等离子体物理研究所, 2008 ZHOU Qian. The basic behaviors of plasma impurities and the particle transport of plasma impurities on the HT-7 tokamak[D]. Hefei:Institute of Plasma Physics, Chinese Academy of Sciences, 2008( 1) 1) |
| 7 | Mcpherson A, Rouze N, Westerveld W B, et al. Calibration of a VUV spectrometer detector system using synchrotron radiation[J]. Applied Optics, 1986, 25(2):298-310. DOI:10.1364/AO.25.000298( 1) 1) |
| 8 | Sato K, Otsuka M, Mimura M. Intensity calibration of a VUV system by branching line pairs of low ionized light-atoms[J]. Applied Optics, 1984, 23(19):3336-3340. DOI:10.1364/AO.23.003336( 1) 1) |
| 9 | 崔正英, 高压东, 傅炳忠, 等. HL-2A 真空紫外光谱空间分布测量及绝对标定[J]. 核聚变与等离子物理, 2011, 31(1):1-6 CUI Zhengying, GAO Yadong, FU Bingzhong, et al. Radial profile measurement and absolutely calibration of VUV spectroscopy in HL-2A tokamak[J]. Nuclear Fusion and Plasma Physics, 2011, 31(1):1-6( 1) 1) |
| 10 | 张洪明, 沈永才, 符佳, 等. EAST 软X射线光谱仪绝对强度标定[J]. 核聚变与等离子体物理, 2013, 33(4):312-319 ZHANG Hongming, SHEN Yongcai, FU Jia, et al. Absolute intensity calibration of soft X-ray spectrometer on EAST[J]. Nuclear Fusion and Plasma Physics, 2013, 33(4):312-319( 2) 2) |
| 11 | Shao C Q, Zhao J Y, Zang Q, et al. Analysis and performance of the Thomson scattering diagnostic on HT-7 tokamak based on I-EMCCD[J]. Plasma Science and Technology, 2014, 16(8):721-725. DOI:/10.1088/1009-0630/16/8/01( 2) 2) |
| 12 | Chen Y J, Wu Z W, Liu X J, et al. Investigation of Zeff and impurity behavior in lithium coating experiments with full metallic first wall in HT-7 tokamak[J]. Plasma Physics and Controlled Fusion, 2015, 57:025012. DOI:10.1088/0741-3335/57/2/025012( 2) 2) |
| 13 | Shi Y J, Lee S G, Hill K W, et al. Inversion technique to obtain local rotation velocity and ion temperature from line-integrated measurements for elongated tokamak plasma[J]. Review of Scientific Instruments, 2012, 83:10D717. DOI:10.1063/1.4733732( 2) 2) |
| 14 | Chowdhuri M B, Ghosh J, Banerjee S, et al. Investigation of oxygen impurity transport using the O4+ visible spectral line in the Aditya tokamak[J]. Nuclear Fusion, 2013, 53:023006. DOI:10.1088/0029-5515/53/2/023006( 3) 3) |
| 15 | Summers H P. The ADAS user manual version 2.6[EB/OL]. http://adas.phys.strath.ac.uk,2004( 1) 1) |
| 16 | Dux R. Technical Report No 10/30[R]. Germany:IPP Garching, 2006( 1) 1) |
| 17 | Cui Z Y, Morita S, Zhou H Y, et al. Enhancement of edge impurity transport with ECRH in the HL-2A tokamak[J]. Nuclear Fusion, 2013, 53:093001. DOI:10.1088/0029-5515/53/9/093001( 1) 1) |
| 18 | 许平. 利用软X 射线能谱诊断研究HT-7 和EAST 等离子体中的中、高Z 杂质行为[D]. 合肥:中国科学院等离子体物理研究所, 2010 XU Ping. Study of medium and high-Z impurity behavior in HT-7 and EAST using soft X-ray PHA diagnostic[D]. Hefei:Institute of Plasma Physics, Chinese Academy of Sciences, 2010( 2) 2) |
| 19 | Lu B, Wang F D, Shi Y J, et al. Upgrade of the high resolution imaging X-ray crystal spectrometers on experimental advanced superconducting tokamak[J]. Review of Scientific Instruments, 2012, 83:10E130. DOI:10.1063/1.4738652( 1) 1) |
| 20 | 陈俊, 吕波, 王福地, 等. 托卡马克弯晶谱仪双晶体结构应用的初步研究[J]. 核技术, 2015, 38(11):110403. DOI:10.11889/j.0253-3219.2015.hjs.38.110403 CHEN Jun, LYU Bo, WANG Fudi, et al. Preliminary study on double-crystal for X-ray curved-crystal spectrometer on EAST[J]. Nuclear Techniques, 2015, 38(11):110403. DOI:10.11889/j.0253-3219.2015.hjs.38.110403( 1) 1) |


