2. 中国科学院大学 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
遗传算法作为一种通用性好、效率高的随机搜索算法,广泛应用于自动控制、图像处理、机器学习、人工智能等领域[1]。在自由电子激光(Free- Electron Laser,FEL)优化中,我们的目标是通过选取合适的磁铁参数,使FEL的辐射功率达到最大。由于该问题的搜索空间较大,使用枚举法等经典搜索方法并不适宜,而遗传算法提供了一种效率高且能有效解决问题的合理方法。此外,使用Java语言构建了一个具有用户界面的应用,使得基于遗传算法的FEL优化变得通用且方便。以下从物理模型、算法设计、程序设计等方面逐一阐述。需要特别指出的是,本文的最终目的是为将来真实的FEL装置调试优化提供可执行的应用程序,所以这里所有的工作都是基于数值模拟计算的,如FEL辐射的计算使用了三维模拟程序Genesis 1.3[2]。
1 物理模型简述自由电子激光是一种相干的同步辐射,当高性能相对论性电子束流通过长波荡器时,电子的扭摆运动将产生这种辐射,指数放大,直至饱和。对于一个实际的FEL装置,优化最终的FEL辐射并不是一件容易的事情,因为涉及到的元件变量太多,比如电子束轨道的矫正和电子束包络大小的优化 等[3, 4]。本文首先利用数值计算程序作为FEL辐射功率的评估手段(实际FEL装置上可实时读取到强度数值),涉及到的变量假定为影响电子束横向包络的两种聚焦铁的强度,这样从遗传算法角度来看,就等效为寻找恰当的聚焦铁的强度使最后得到的辐射强度最大。
为程序的通用性和扩展性,我们把计算FEL辐射的功能做成一个Python数值计算模块,类似地,其他优化功能可以按照相同的思路编写计算模块;当使用在真实的FEL装置上时,额外要做的就是把计算模块中的计算模拟部分替换成实时的反馈源。
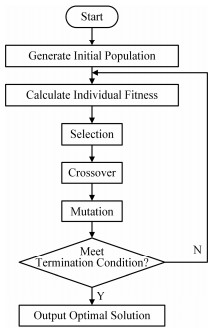
2 算法概述所谓遗传算法,就是选择适当的编码方式,将变量表达为一个数字串,来模仿生物进化过程中的遗传基因和染色体串,通过三个基本操作:选择、交叉、变异,模拟自然进化过程来搜索最优解[5, 6]。遗传算法实现的流程图如图 1所示。
|
图1 算法流程图 Fig.1 Flow chart of the algorithm. |
初始种群在变量取值范围内随机选取,种群个体数根据变量范围和需求精度作相应调节,以迭代次数作为终止条件。
遗传算法常用的编码方式有二进制编码、序列编码、实数编码等[6, 7]。在FEL多变量优化这个问题上,由于参数区间未知,即问题空间的大小不定,采用简单的二进制编码会造成编码冗余的情况,而且解码过程也较复杂。考虑以上因素,我们选择实数编码方式,即直接采用问题变量进行编码,无需解码过程。该编码方式具有精度高、便于大空间搜索等优点[8]。
在本文设计的算法中,我们选用锦标赛法作为选择操作的方法[7],并将其优化为:假设种群中共有n个个体,xi记为第i个个体,i从1到n遍历,另一个体从种群中任意选取,记为xrand。比较xi与xrand,将适应度较高的保存到下一代。这样既可以保证优胜劣汰,又能使种群中的每个个体都参与到选择操作中,从而保证算法的可靠性。
遗传算法的交叉就是将两个父代个体通过重组产生新的子代个体的操作。由于我们选用的是实数编码的编码方式,常规的用于二进制编码的交叉算子并不适用。对比几种实数编码常用的交叉算子,最后选择中间重组交叉的方法[7, 9]。采用中间重组交叉方式产生的子代解向量的搜索空间小于父代,即中间重组交叉使得解空间不断收敛,便于更快速寻找到最优解。
| ${x}'=x\pm 0.5L\Delta $ | (1) |
式中:x为父代个体;x'为变异后的子代个体;$L={{x}_{\max }}-{{x}_{\min }}$,为变量的取值范围;$\Delta \text{=}\sum\nolimits_{i=0}^{m}{(a(i)/{{2}^{i}})}$,m=20,a(i)以1/m的概率取1,以1−1/m的概率取0,因此$\Delta \in [0,1)$。
当x≥xmin+0.5L时,
| ${x}'=x-0.5L\Delta $ | (2) |
此时,xmin<x'≤x。
当x<xmin+0.5L时,
| ${x}'=x\text{+}0.5L\Delta $ | (3) |
此时,x≤x'<xmax。这样可以保证经过变异后,子代个体不会超出变量的取值范围。
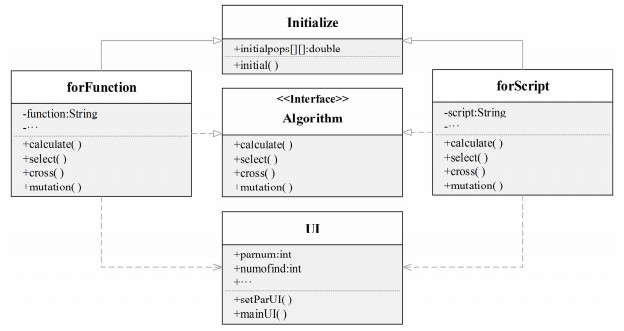
3 程序设计及功能介绍为使该算法足够通用且易于扩展,我们使用Java语言设计了一个应用程序,并用Java swing构建了一个简洁、友好的用户界面[10]。程序框架如图 2所示。
|
图2 应用程序UML类图 Fig.2 UML class diagram of the application. |
forFunction类和forScript类表示目标函数的两种不同表达方式,即函数表达式形式和脚本文件形式。他们都继承自Initialize类,并实现Algorithm接口。覆写了Algorithm类中实现遗传算法操作的calculate、select、cross、mutation等方法。同时,两个类直接依赖于UI类,从UI类中读取设置参数,并将输出结果返回给UI显示。
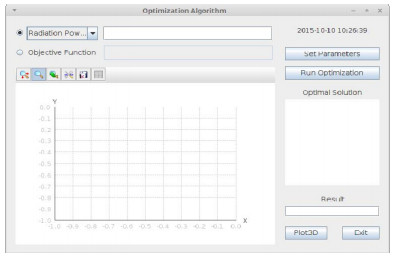
应用程序的主界面如图 3所示。下拉菜单中的可选项表示该应用可以实现的功能,当前仅有Radiation Power一项,用于优化辐射强度,还可扩展其他优化功能,如光谱带宽等。考虑到不同功能对应不同的模拟计算过程,我们把模拟计算过程写入相应的脚本文件,并将其转变为可执行命令,写入后面的文本输入区域。利用Java语言特有的Runtime类来实现脚本的解析与执行,脚本返回每一个子代的目标函数评估结果。此外,也预留了另外一个选项:Objective Function,用于输入显式的目标函数,解决常规的优化问题,同时也可以用来测试算法的效率和可靠性。
|
图3 应用程序主界面 Fig.3 Main interface of the application. |
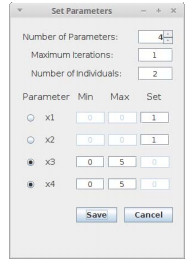
参数设置的界面如图 4所示。其中Number of Parameters表示变量个数,在该应用程序中设置为2-5个变量可调。不同优化问题对变量的要求不同,为提高算法的通用性使其能适用于不同问题的优化,加入Precision项表示变量的精度。Maximum iterations为最大迭代次数,即算法的终止条件。由于不同问题变量的取值范围不同,而算法的效率和精度很大程度取决于种群个体数,引入Number of individuals这一可变量不仅可以控制解决不同问题种群个体数的设置,还可以通过不断调整与测试,找出各个特定优化问题最合适的种群个体数。每个参数前都有一个选择按钮,当其被选中时,表明该参数可调,即需要优化的参数,调节范围为[Min,Max]。未被选中的参数视为固定值Set。这样的设置可以提高程序的通用性和灵活性,当某个输出量受多个参数影响,但是只希望调节其中某几个参数来优化结果时,图 4界面的优势就体现出来。
|
图4 参数设置界面 Fig.4 Interface of the parameter setting. |
由于Java语言的跨平台特性,该应用程序可以运行在任意安装有Java运行环境的机器上。
4 实验结果为验证算法的实际效率以及实用性,我们从显式目标函数和脚本文件输入两方面进行了测试。
4.1 显式函数以4个变量的二次函数为例,表达式为:
| $F(x)=-\sum\nolimits_{i=1}^{4}{({{10}^{n-1}}\times x_{i}^{2})}\ \ \ -10<{{x}_{i}}<10$ | (4) |
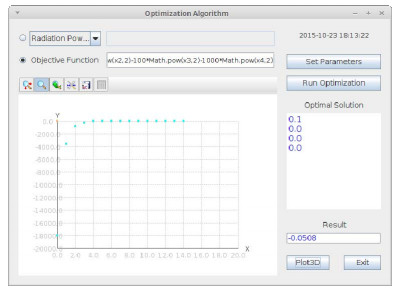
当xi=0时,该函数有最大值,最大值为0。下面测试Optimization Algorithm这一应用在解决这一函数求最大值问题上的效率和结果。相应的参数设置:精度为0.1,最大迭代次数为15,种群个体数为40。图 5是优化结果,与实际最大值仅相差0.05左右。实验证明,增加种群个体数会使结果更优。
精度为0.1时,4个区间在(-10,10)的变量通过遍历寻找函数最大值,最坏情况下需要计算约2004次。而此处利用该算法,只需计算600次。可见该算法大大降低了解决该问题的时间复杂度,也就直观地验证了算法的效率。并且从图 5可知,迭代至第5次,即可达到最大值,表明该算法的收敛速度较快。
|
图5 目标函数优化结果 Fig.5 Optimization results of objective function. |
以上实例表明,该算法在解决这类多变量函数最值问题时,无论从效率还是结果上都具有说服力。该应用程序在多次测试和使用中也未出现Bug。
4.2 FEL辐射强度优化基于遗传算法开发这一应用的本质目的是用于解决FEL上的具体优化问题。以辐射强度优化为例测试该应用在解决具体问题时的表现。
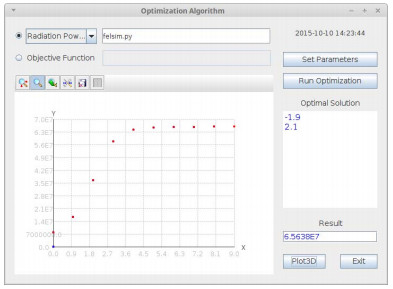
使用Python语言将FEL辐射强度的模拟计算过程写入felsim.py脚本(如图 6所示,该封装好的Python脚本为系统可执行程序),传入参数为一对四极磁铁的强度(QF,QD),输出为FEL辐射强度,脚本中调用Genesis 1.3进行FEL辐射的模拟计算。变量(QF,QD)的最大取值范围设置为[-5,5],单位为T∙m−1,不同的QF和QD代表电子束流的不同横向包络大小。考虑到实际情况对磁铁强度的精度要求并不那么高,在此我们把精度取为0.1,每代种群的个体数为40,迭代次数为10,得到的优化结果如图 6所示。
|
图6 FEL辐射强度优化结果 Fig.6 Optimization results of the radiation power of FEL. |
结果表明当(QF,QD)=(-1.9,2.1)时,获得的辐射强度最大值为65.638MW。总计算次数为400次。
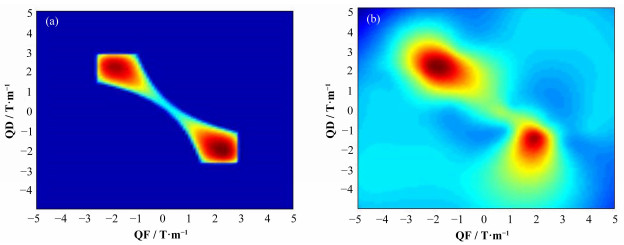
图 7(a)表示$(\operatorname{QF},\operatorname{QD})\in [-5,5]$、精度为0.1时全局遍历的结果,遍历次数为10201次。从图 7(a)中可以看出,在取值范围内,辐射强度有两个峰值。当(QF,QD)=(2.2,-1.8)时,辐射强度取最大值,为66.665MW,即右下角峰值点,当(QF,QD)=(-1.9,2.1)时,辐射强度为65.638MW,即左上角峰值点,这与图 6的结果一致。图 7(b)为在上述参数条件下,优化算法得到的所有400次计算结果。两幅图对比可以看出,优化算法得到的峰值区域与遍历的结果几乎一致。计算可知优化算法得到的最优解与实际最优解仅有1.5%的误差。需要强调的是,遗传算法作为一种随机算法,其时间复杂度并不是固定的,而我们在利用遗传算法解决FEL多变量优化问题时,只需找到满足要求的近似最优解即可。上述结果在精确度和效率上都符合我们的要求。
|
图7 全局遍历(a)与算法优化(b)对比图 Fig.7 Comparison charts of global traversal (a) and algorithm optimization (b). |
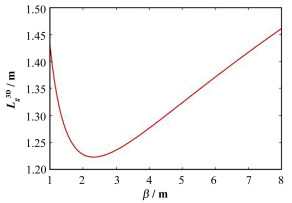
需要说明的是,本例仅作为遗传算法和该程序在FEL优化上应用的一个简单验证,因此仅简单考虑了聚焦磁铁强度与辐射功率的关系。结果显示,遗传算法的优化结果对应的β函数(约4m)与解析优化的β函数(如图 8所示)比较吻合,进一步表明该算法的准确和高效。
|
图8 解析的β函数曲线 Fig.8 Analytic β function curve. |
为验证该算法的稳定性,我们将上述过程重复执行50次,得到结果如图 9所示。
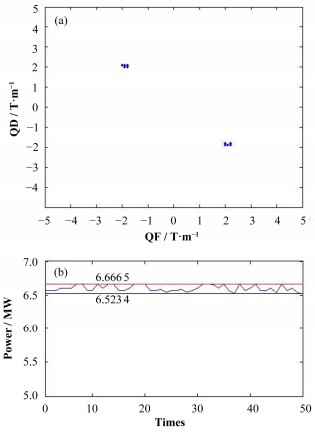
图 9(a)中可以看出,50次重复实验得到的优化解分布在两块很小的区间范围之内,而这两块区域与图 7中的两处峰值相对应,表明多次重复实验的过程中并未出现不合理的优化解。图 9(b)是50次重复实验对应的辐射强度的最大值,波动范围约2.1%。图 9有力地证明了该算法拥有相当高的可靠性和稳定性。
|
图9 重复实验结果(a)及对应的辐射强度的最大值(b) Fig.9 Results of repeated experiments (a) and the maximum value of the corresponding radiation intensity (b). |
以上工作证明,该优化算法和设计的软件在解决常规显式目标函数最值问题上表现优越。在优化FEL辐射强度的问题上,也可以在短时间内寻求到一组合适的解向量,使得辐射强度达到近似最优值。即该应用在效率和功能上都满足我们解决FEL辐射强度优化的问题。需要指出的是,FEL优化是一个复杂的系统性问题,在今后的工作中需要改进与完善,以使其能更好地应用在真实的装置调试环境中,比如:扩展应用程序的功能,使其更通用,不仅用于解决FEL辐射强度的优化,还能用于解决光谱等其他量的优化问题等。
| 1 | 吉根林. 遗传算法研究综述[J]. 计算机应用与软件, 2004, 21(2):69-73 JI Genlin. Overview of genetic algorithms[J]. Computer Applications and Software, 2004, 21(2):69-73( 1) 1) |
| 2 | Reiche S. GENESIS 1.3:a fully 3D time-dependent FEL simulation code[J]. Nuclear Instruments and Methods in Physics Research, 1999, A429(1):243-248( 1) 1) |
| 3 | Meier E, Biedron S G, LeBlanc G, et al. Development of a novel optimization tool for electron linacs inspired by artificial intelligence techniques in video games[J]. Nuclear Instruments and Methods in Physics Research, 2011, A632(1):1-6( 1) 1) |
| 4 | Huang X, Corbett J, Safranek J, et al. An algorithm for online optimization of accelerators[J]. Nuclear Instruments and Methods in Physics Research, 2013, A726(1):77-83( 1) 1) |
| 5 | 王小平, 曹立明. 遗传算法:理论, 应用及软件实现[M]. 西安:西安交通大学出版社, 2002 WANG Xiaoping, CAO Liming. Genetic algorithm:theory, application and software implementation[M]. Xi'an:Xi'an Jiao Tong University Press, 2002( 1) 1) |
| 6 | 吉志龙, 马元巍, 王德忠. 遗传算法动态修正核素大气扩散模型的适应度函数研究[J]. 核技术, 2014, 37(4):040503. DOI:10.11889/j.0253-3219.2014.hjs.37.040503 JI Zhilong, MA Yuanwei, WANG Dezhong. The fitness function of genetic algorithm for dynamic correction of the atmospheric dispersion model[J]. Nuclear Techniques, 2014, 37(4):040503. DOI:10.11889/j.0253-3219.2014. hjs.37.040503( 2) 2) |
| 7 | 田小梅, 龚静. 实数编码遗传算法的评述[J]. 湖南环境生物职业技术学院学报, 2005, 11(1):25-31 TIAN Xiaomei, GONG Jing. A review of real coded genetic algorithm[J]. Journal of Hunan Vocational College of Environmental Biology, 2005, 11(1):25-31( 4) 4) |
| 8 | 雷德明. 多维实数编码遗传算法[J]. 控制与决策, 2000, 15(2):239-241 LEI Deming. Multidimensional real-coded genetic algorithm[J]. Control and Decision Making, 2000, 15(2):239-241( 1) 1) |
| 9 | 邝航宇, 金晶, 苏勇. 自适应遗传算法交叉变异算子的改进[J]. 计算机工程与应用, 2006, 42(12):93-96 KUANG Hangyu, JIN Jing, SU Yong. Genetic algorithm with adaptive crossover and mutation operator improved[J]. Computer Engineering and Applications, 2006, 42(12):93-96( 2) 2) |
| 10 | Eckel B, 陈昊鹏. Java 编程思想[M]. 北京:机械工业出版社, 2002 Eckel B, CHEN Haopeng. Thinking in Java[M]. Beijing:Machinery Industry Press, 2002( 1) 1) |


