在超临界状态下，液态水和汽态水是没有明显分界点的。在超临界区，用拟临界阶段状态点（拟临界点）作为区分拟液态和拟汽态的分界点。在拟临界点时，对应的温度值为拟临界点温度值，对应此时的定压比热容达到最大值。在超临界水从液态向汽态逐渐转变的过程中，其热力学的各种物性参数会有着各种较为奇特的变化趋势。所以在这些物性参数中，热膨胀系数作为一个导出变量，是一个重要的参数。该参数在超临界核反应堆的流动不稳定性及换热分析计算中具有重要的应用。Ambrosini等^[1]在分析超临界压力下的流动不稳定的时候，提出了临界相变转换数(Trans-pseudocritical Number, NTPC)的概念。在临界相变转换数的计算公式中，拟临界点热膨胀系数是其中需要计算的一个重要变量。拟临界点的膨胀系数，即为在一定超临界压力下，对应在拟临界温度点时的热膨胀系数。值得一提的是，“超临界热膨胀系数”跟“拟临界点的热膨胀系数”两者概念是不同的。“超临界热膨胀系数”是在一定压力下，随着温度变化时由连续变化的一组数值组成。而“拟临界点的热膨胀系数”是“超临界热膨胀系数”中的峰值点^[2]。计算超临界水在拟临界点的热膨胀系数，对于理解和掌握超临界水堆中能量的转换或热量的传递非常重要。在能源动力工程中的其他各个领域分析研究中，超临界水的拟临界点的热膨胀系数的计算亦有着重要而广泛的应用。但是在大量的能源与动力类的文献[2−7]中，超临界水的拟临界点的热膨胀系数的具体计算数值却鲜有报道。依据国际水和水蒸汽性质协会(International Association for the Properties of Water and Steam, IAPWS)提供的1997年工业用计算标准(IAPWS-IF97)^[8]，利用液态水和汽态水的热膨胀系数差值计算的方法，可以直接计算得到在不同超临界压力下的液态水和汽态水的热膨胀系数。确定拟临界点温度之后，从而可以相应得到拟临界点的热膨胀系数。但是直接计算时，计算工作量往往过大，且计算过程较为繁琐。超临界水的拟临界点的热膨胀系数计算模型的提出，能够简单迅速地计算得到在各种不同压力下的拟临界点的热膨胀系数值，且精度范围满足超临界水的拟临界点的热膨胀系数分析的要求。该公式的提出，为进一步编程分析计算超临界水的相变转换数等参数具有重要意义，为便捷快速地量化分析超临界水的流动换热特性奠定了基础，有利于更好地对超临界水进行流动不稳定性分析。

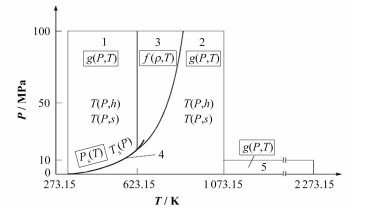
IAPSW-IF97公式将液态水和汽态水的整个有效区域划分为5个子区域，如图 1所示。

图 1

图 1 IAPWS-IF97的分区 Figure 1 IAPWS-IF97 subregion.

在图 1中的分区计算公式中，第三区为超临界区，为需要计算热膨胀系数的区域。其中划分第三区和第二区的边界计算公式为：

式中：$\pi=P/{{P}^{*}}$；$\theta=T/{{T}^{*}}$。其中：P^*=1 MPa；T^*=1 K。

超临界区的计算公式适用范围如下：623.15K≤T≤T(P)_Eq.(1)，P_s(T)≤P≤100MPa。

式中：$\delta=\rho/{{\rho }^{*}}$；$\tau={{T}^{*}}/T$。其中：${{\rho }^{*}}={{\rho }_{\text{c}}}$；${T^*}={T_{\rm{c}}}$。R=0.462 kJ (kg ·K)^-1；T_c=647.1 K；p_c=22.064 MPa；ρ_c=322 kg ·m^-3；P为压力，MPa。式(2)中的n_i、I_i、J_i均为IAPWS-IF97计算标准^[8]中的计算系数参数。

根据工程热力学的定义，液态水和汽态水的热膨胀系数是在等压情况下比体积随着温度的变化率。计算公式如下：

式中：β_p为热膨胀系数，K⁻¹；ν为比体积，m³·kg⁻¹；T为热力学温度，K。

在超临界区域范围内，第三区给出的基本方程形式是Helmholtz比自由能方程f(ρ, T)（对应的无量纲形式的Helmholtz比自由能方程为$\varphi(\delta, \tau)$）。在超临界区域中，$\varphi(\delta, \tau)$以折算密度δ和折算温度τ为独立的变量。压力的关系表达式如下：

式中：ρ为密度，kg·m⁻³；${\varphi _\delta }$为$\varphi(\delta, \tau)$对折算密度的偏导数；基准密度ρ_c=322 kg·m⁻³。

因为在超临界区域中给出的基本方程不是直接以P和T为独立变量的，所以，要使用隐含导数求导的方法，将P看成是相对于T独立的变量，然后将压力的关系方程两边同时对T求偏导数，即：

解上述方程可得：

将式(6)带入热膨胀系数的定义式(3)中，得到热膨胀系数的计算公式如下：

式中：${\varphi _{\delta \tau }}$为$\varphi(\delta, \tau)$对折算密度和折算温度的二阶偏导数；${\varphi _{\delta \delta }}$为$\varphi(\delta, \tau)$对折算密度的二阶偏导数。

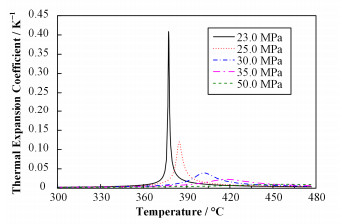
当水在超临界状态下，液态水和汽态水是没有明显分界点的。当水处于温度较低时，可以认为此时水的状态是和亚临界以下的液态水是一致的。当水处于温度较高时，可以认为此时水的状态是和亚临界以下的汽态水是一致的。但是在从液态水向汽态水过渡的过程中，此时处于一种液态水和汽态水的混合状态。在一定的压力条件下，在某一临界温度点附近时，此时液态水和汽态水的热膨胀系数达到最大值，之后迅速减小。超临界水在不同压力条件下的热膨胀系数变化趋势如图 2所示。

图 2

图 2 不同压力下超临界水的热膨胀系数变化趋势 Figure 2 Thermal expansion coefficient of supercritical water under different pressure.

由图 2可见，在压力一定的条件下，超临界水在从液态水向汽态水状态转变的过程中，热膨胀系数首先迅速升高，达到峰值之后又迅速下降。超临界水的热膨胀系数所对应的温度在拟临界温度点附近，此时的热膨胀系数为拟临界点的热膨胀系数。随着压力的升高，拟临界点的热膨胀系数的峰值逐渐降低，同时对应的拟临界温度值却在逐渐升高。

通过对式(3)进行差值计算，选择其中热膨胀系数的峰值，从而得出不同压力下的拟临界点的温度值和拟临界点的热膨胀系数的数值，如表 1所示。

表 1

表 1 不同压力对应的拟临界点的热膨胀系数 Table 1 Pseudo-critical thermal expansion coefficient under different pressure. 序号No. 压力Pressure / MPa 拟临界温度Pseudo-critical temperature / °C 拟临界点的 热膨胀系数Pseudo-critical thermal expansion coefficient / K−1 1 22.1 374.04 3.52 2 22.2 374.40 2.38 3 22.3 374.78 1.63 4 22.5 375.53 0.91 5 23.0 377.35 0.41 6 24.0 381.10 0.19 7 25.0 384.75 0.12 8 26.0 388.35 0.087 9 27.0 391.85 0.067 10 28.0 395.25 0.055 11 29.0 398.65 0.046 12 30.0 401.85 0.039 13 31.0 404.75 0.034 14 33.0 411.65 0.028 15 35.0 417.75 0.023 16 40.0 432.35 0.016 17 50.0 458.35 0.0099

表 1 不同压力对应的拟临界点的热膨胀系数 Table 1 Pseudo-critical thermal expansion coefficient under different pressure.

通过表 1计算得出超临界水的拟临界点的热膨胀系数，可以直观地看出在各种压力下的拟临界点的热膨胀系数数值的大小，可以供相关研究人员对超临界压力下的水的拟临界点的热膨胀系数进行查询参考使用。

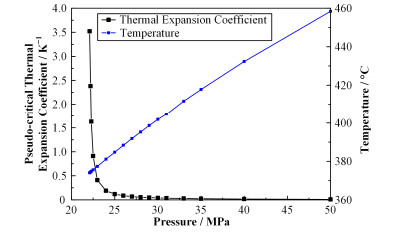
在不同压力下的超临界水拟临界温度值和拟临界点的热膨胀系数的变化趋势情况如图 3所示。

图 3

图 3 拟临界温度和拟临界点的热膨胀系数变化趋势 Figure 3 Trend of pseudo-critical temperature and pseudo-critical thermal expansion coefficient.

通过图 3可以看出，随着压力升高，超临界水的拟临界温度值逐渐升高，而超临界水的拟临界点的热膨胀系数是迅速下降的，下降速度呈现为指数级别的速度下降。当下降到一定程度之后，拟临界点的热膨胀系数变化趋势趋于平缓，说明达到一定压力之后，随着温度的变化，超临界水的热膨胀变化是比较小的。

由于在表 1中计算所得的各压力下的拟临界点的热膨胀系数是通过逐点温度差值计算热膨胀系数而得到的，计算工作量较大，且工作较为繁琐。所以根据表 1中计算得到的拟临界点的热膨胀系数的原始数据，利用MATLAB拟合数据工具箱对超临界水的拟临界点的热膨胀系数值进行了拟合分析。通过拟合分析得到了如下两种公式结构的拟合公式，计算结果的回归情况较为理想。拟合公式分别如下：

拟合公式一：

式中：a₁=0.568(0.504, 0.632)；b₁=−21.94(−21.96, −21.92)。

拟合公式二：

式中：c₁=0.327(0.317, 0.337)；c₂=−7.112(−7.342, −6.882)；d₁=−44(−44.01, −43.98)；d₂=484(483.7, 484.3)。其中括弧内的系数参数范围为回归系数为95%置信区间的界限参数。

拟合公式一和拟合公式二计算拟临界膨胀系数的计算结果及相对误差和绝对误差如表 2、3所示。

表 2

表 2 拟合公式一和拟临界点的热膨胀系数的结果对比 Table 2 Contrast of pseudo-critical thermal expansion coefficient with the result of fitting Formula 1. 压力Pressure / MPa 直接计算结果 Directly calculation result / K−1 计算结果 Calculation result / K−1 绝对误差 Absolute error / K−1 相对误差 Relative error / % 22.1 3.52 3.55 0.028 0.008 1 22.2 2.38 2.18 −0.20 −0.083 22.3 1.63 1.58 −0.051 −0.031 22.5 0.91 1.01 0.10 0.11 23 0.41 0.54 0.13 0.31 24 0.19 0.28 0.087 0.46 25 0.12 0.19 0.066 0.55 26 0.087 0.14 0.053 0.61 27 0.067 0.11 0.045 0.67 28 0.055 0.094 0.039 0.71 29 0.046 0.080 0.035 0.75 30 0.039 0.070 0.031 0.79 31 0.034 0.063 0.028 0.82 33 0.028 0.051 0.024 0.86 35 0.023 0.043 0.021 0.90 40 0.016 0.031 0.015 0.97 50 0.009 9 0.020 0.010 1.04

表 2 拟合公式一和拟临界点的热膨胀系数的结果对比 Table 2 Contrast of pseudo-critical thermal expansion coefficient with the result of fitting Formula 1.

表 3

表 3 拟合公式二和拟临界点的热膨胀系数的结果对比 Table 3 Contrast of pseudo-critical thermal expansion coefficient with the result of fitting Formula 2. 压力 Pressure / MPa 直接计算结果 Directly calculation result / K−1 计算结果 Calculation result / K−1 绝对误差 Absolute error / K−1 相对误差 Relative error/ % 22.1 3.52 12.13 8.61 2.45 22.2 2.38 3.85 1.47 0.62 22.3 1.63 2.08 0.45 0.27 22.5 0.91 1.01 0.099 0.11 23 0.41 0.42 0.007 1 0.017 24 0.19 0.19 −0.003 4 −0.018 25 0.12 0.12 −0.001 1 −0.008 9 26 0.087 0.087 0.000 64 0.007 4 27 0.067 0.069 0.001 7 0.025 28 0.055 0.057 0.002 3 0.042 29 0.046 0.049 0.002 6 0.057 30 0.039 0.042 0.002 8 0.071 31 0.034 0.037 0.003 0 0.086 33 0.028 0.030 0.002 9 0.11 35 0.023 0.026 0.002 8 0.12 40 0.016 0.018 0.002 5 0.16 50 0.009 9 0.012 0.001 9 0.19

表 3 拟合公式二和拟临界点的热膨胀系数的结果对比 Table 3 Contrast of pseudo-critical thermal expansion coefficient with the result of fitting Formula 2.

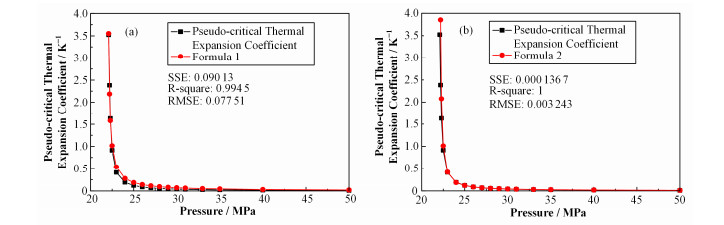
为了将表 2、3中的拟合公式计算结果进行直观对比，表 2、3中直接计算结果和拟合公式一和拟合公式二得出的结果对比情况如图 4所示。

图 4

图 4 直接计算结果和拟合公式一(a)、拟合公式二(b)计算结果的对比 Figure 4 Contrast of directly calculation result with the result of fitting Formula 1 (a) and fitting Formula 2 (b).

通过图 4中拟合公式中的计算结果和直接计算得出的拟临界点的热膨胀系数的对比可以看出，拟合公式一在压力较低时与实际计算得出的数值误差较小，但是压力超过23MPa之后拟合公式一得出的计算结果普遍比实际值偏高。拟合公式二的误差平方和(Sum of the Squared Errors, SSE)跟公式一的误差平方和相比较小，均方根误差(Root Mean Square Error, RMSE)也比公式一的均方根误差要小很多。拟合公式二的回归系数为1，表明拟合结果的实际趋势和实际计算结果的趋势是完全线性相关的。但是在压力低于23MPa的压力范围内，通过拟合公式二计算得出的结果跟拟合公式一相比偏高较多。

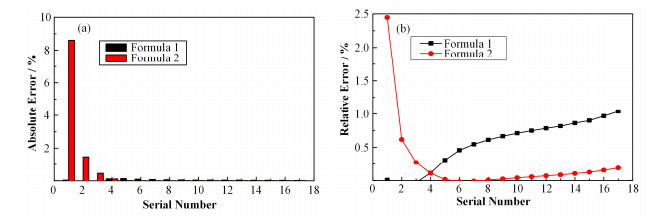
拟合公式一和拟合公式二的计算结果的绝对误差和相对误差分布情况如图 5所示。通过图 5(b)在公式一和公式二的相对误差分布情况也可以看出，在压力较低时公式一的相对误差较小，在压力较高时公式二的相对误差较小。所以综合考虑后确定，当超临界压力小于等于22.5MPa时，建议选用公式一；当超临界压力大于等于23.0MPa时，建议选用公式二。当超临界压力介于22.5MPa和23.0MPa之间时，则采用拟合公式一和拟合公式二组合的方式计算。具体组合过渡形式见§3.4的最终公式。组合计算形式的采用，保证了拟临界点的热膨胀系数的计算在不同压力区间变化时的计算结果具有连续光滑性。

图 5

图 5 拟合公式一与拟合公式二的绝对误差(a)和相对误差(b)对比 Figure 5 Absolute error contrast (a) and relative error contrast (b) between fitting Formula 1 and fitting Formula 2.

经过§3.3的误差分析，最终确定的公式形式如式(13)所示：

式中：a₁=0.568(0.504, 0.632)；b₁=−21.94(−21.96, −21.92)；c₁=0.327(0.317, 0.337)；c₂=−7.112(−7.342, −6.882)；d₁=−44(−44.01, −43.98)；d₂=484(483.7, 484.3)。

用IAPWS-IF97标准计算拟临界点的热膨胀系数时，需要首先计算已知压力下对应的拟临界点温度，进而通过压力和温度，计算出该压力和温度下的热膨胀系数，即拟临界点的热膨胀系数。而采用新拟合的式(13)计算拟临界点的热膨胀系数时，由于拟临界点的热膨胀系数是压力的函数，所以仅知道压力，即可通过拟合公式求出该超临界压力下对应拟临界点的热膨胀系数。对比该两种不同的计算方法，运用本文公式可以加快反应堆程序的计算速率，进而减少计算时间。

根据液态水和汽态水的热膨胀系数计算定义，直接计算得出了超临界水在各个压力下的拟临界点的热膨胀系数。然后根据直接计算得出的各个压力下的拟临界点的热膨胀系数，运用MATLAB曲线拟合工具箱，对超临界水的拟临界点的热膨胀系数进行了拟合回归分析，并得出了两组计算超临界水的拟临界点的热膨胀系数的计算公式。

1)超临界水拟临界点的热膨胀系数，在临界点附近时达到最大值，随着压力的上升，拟临界点的热膨胀系数迅速下降，当压力超过25.0MPa之后，拟临界点的热膨胀系数的变化趋于平缓。

2)当超临界压力低于22.5MPa时，建议选用拟合公式一计算拟临界膨胀系数；当超临界压力大于等于23.0MPa时，建议选用拟合公式二计算拟临界膨胀系数。当压力介于22.5MPa和23.0MPa之间时，采用上述两公式组合的方式进行计算。最终推荐计算公式形式如式(13)所示。最终计算公式最大的绝对误差为0.201K⁻¹，最大的相对误差为0.19%，满足计算分析拟临界点的热膨胀系数的要求，且具有结构简单易于编程计算的特点。