2. 中国科学院高能物理研究所 核分析技术重点实验室 北京 100049
2. Key Laboratory of Nuclear Analysis Techniques, Institute of High Energy Physics, Chinese Academy of Sciences, Beijing 100049, China
航天器在轨飞行期间将遭遇复杂的辐射环境,如辐射带捕获粒子、太阳高能粒子和银河宇宙射线,它们与航天器材料相互作用,在材料中沉积电荷,影响材料的性能。研究表明,能量足够高的电子能穿透航天器的结构、屏蔽层或者仪器外壳,停留在电缆绝缘层、电路板以及其他介质层中而引起电荷沉积[1]。由于介质的导电率非常低,因此电荷不断累积。一旦累积的电荷足够高,其电场强度超过材料的击穿阈值时,就会引起放电,这种现象称为深层介质充放电。据国外有关资料统计,空间环境引起的航天器异常和失效故障中,深层介质充放电占到25%左右[2-4]。近年来,随着航天器飞行轨道越高,且在轨飞行时间加长,高能电子引起的介质材料深层充放电效应越来越严重。为此,本文从不同电子能量、不同介质厚度以及不同金属层角度分析了介质材料深层充放电情形,结合数值模拟仿真分析的方法,研究不同因素对充电所致最大电荷沉积的影响。
1 介质深层充电模型 1.1 介质深层充电模型高能电子与介质材料相互作用的充电过程包括两个方面:一方面,高能电子穿透介质表面进入介质材料内部,不同能量的电子沉积于介质中不同的深度,从而在介质内部产生一定的电荷分布并建立电场;另一方面,因为介质本身有一定的电导率,并且航天器构件的介质材料多为高分子聚合物,在受到辐照时会形成辐射诱导电导率,比没有辐照时的暗电导率大得多,因此在电场作用下会形成泄漏电流,该过程与电荷沉积过程的作用是互为相反的[5-6]。当这两个过程达到动态平衡时,介质中的电场便达到最大,如果该最大电场大于介质材料的击穿阈值,则会发生放电。介质深层充电所产生的电场主要取决于高能电子能谱、介质的电学特性、介质厚度、屏蔽厚度等因素,同时还与卫星在高能电子环境中运行时间有关[7-9]。另外,介质构件的不同接地方式也会影响电场。
由于航天器上常用的印制电路板材料为环氧树脂(Tetrafunctional Epoxy Resin, FR4),是典型的介质材料,因此选取FR4为研究对象,分析介质深层充电现象。为详细分析介质深层充电过程中空间电荷、最大电场、表面电位等电荷输运特性,构建了平板型结构的电荷输运模型。
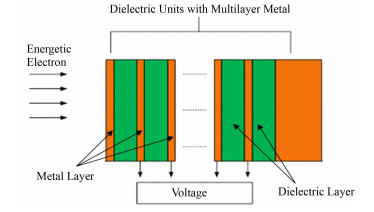
如图 1所示,若图 1中的介质层中间不夹杂金属层时,高能电子与介质材料相互作用过程中会将能量转移给介质材料原子。由于能量不断地衰减,入射原子的速度会越来越慢,最后沉积在材料中;当介质内电荷沉积的速率超过电荷泄露速率时,就会产生内部电荷积聚,引起内电场不断增强,这个过程是一个入射不断沉积并建立内电场,同时产生泄露电流的动态过程。
|
图 1 介质深层充放电物理机制模型 Figure 1 Model of dielectric deep charging-discharging. |
在构建介质深层充电模型的基础上,利用数值模拟方法仿真分析纯介质以及介质层与金属层叠合后的电荷沉积和能量沉积分布特性。
当高能电子垂直入射到一定厚度的介质中时,会与介质碰撞、散射而逐渐将能量转移给介质,最后沉积在介质中或穿透介质。高能电子在无限厚的介质平板中的最大射程可由Webber半经验公式表示为[10]:
| $R=0.55{{E}_{\text{e}}}\left[1-\frac{0.948\ 1}{1+3{{E}_{\text{e}}}} \right]$ | (1) |
式中:Ee为电子束能量,MeV;R为最大射程,g ·cm-2。
实际入射深度x与R之间的关系为:
| $ R=\rho x $ | (2) |
式中:ρ为材料的密度,g ·cm-3。不同能量电子在Al和FR4材料中射程如表 1所示。
| 表 1 不同能量电子在材料中的射程 Table 1 Range of electrons in material under different energy. |
电荷沉积的过程中,其电荷分布可用泊松方程和电荷连续性方程描述[11],其一维形式为:
| $ \varepsilon \frac{\partial E}{\partial x}=\rho $ | (3) |
| $ -\frac{\partial \rho }{\partial t}=\frac{\text{d}{{J}_{0}}}{\text{d}x}+\frac{\partial \left(gE \right)}{\partial x} $ | (4) |
式中:ε为介电常数;E为电场强度;ρ为电荷的密度;J0为高能电子入射带来的电流密度;g为电导率。在辐射条件下,介质电导率为:
| $ g={{g}_{\text{d}}}+{{g}_{\text{r}}}={{g}_{\text{d}}}+\kappa {{\dot{D}}^{\Delta }} $ | (5) |
式中:gd为介质的暗电导率;gr为辐射条件下的介质辐射诱导电导率,可以近似认为它与辐射剂量率Ḋ成一定的指数关系,指数为Δ,比例为κ。J0和Ḋ由MC仿真计算得到,不随时间变化。
将上述方程的偏微分形式近似为小步长的演化方程:
| $ E\left(x+\Delta x, t+\Delta t \right)-E\left(x, t+\Delta t \right)=\frac{1}{\varepsilon }\rho \left(x, t+\Delta t \right)\Delta x $ | (6) |
| $ \begin{align} &\rho \left(x, t+\Delta t \right)-\rho \left(x, t \right)=\\ &\begin{matrix} {} &{} &{} \\ \end{matrix}-\left(\frac{\Delta {{J}_{0}}\left(x \right)}{\Delta x}+\frac{\Delta \left(g\left(x \right)E\left(x, t \right)\right)}{\Delta x} \right)\Delta t \\ \end{align} $ | (7) |
其中:初始条件为E(x, 0)=0、ρ(x, 0)=0。
假定一个很小的时间步长Δt,由电荷连续性方程得到在各位置处的自由电荷分布(方程右侧均为上一时刻的已知值):
| $ \begin{align} &\rho \left(x, t+\Delta t \right)=\rho \left(x, t \right)- \\ &_{{}}^{{}}\left(\frac{\Delta {{J}_{0}}\left(x \right)}{\Delta x}+\frac{\Delta \left(g\left(x \right)E\left(x, t \right)\right)}{\Delta x} \right)\Delta t \end{align} $ | (8) |
而后由各位置处的电荷分布依据泊松方程计算出此时刻的电场分布及电势分布:
| $ E\left(x+\Delta x, t+\Delta t \right)=E\left(x, t+\Delta t \right)+\frac{1}{\varepsilon }\rho \left(x, t+\Delta t \right)\Delta x $ | (9) |
| $ U\left(x+\Delta x, t \right)=U\left(x, t \right)-E\left(x, t \right)\Delta x $ | (10) |
根据介质接地条件的不同,初始边界条件主要有三种情况:
1)对于背面接地的情形,接地面电势为0,入射面电场强度为0,即:E(0, t)=0,U(d, t)=0。其中:d为介质厚度。
2)对于正面接地的情形,其背面对外电场为0,而其正面电势为0,即:E(d, t)=0,U(0, t)=0。
3)对于两面接地的情形,正面及背面电势均为0,即:U(0, t)=U(d, t)=0。
1.3 介质层和金属层叠合后的电荷沉积特性分析对于导体而言,不存在自由电子的俘获过程,并且由于其电导率很大,沉积电荷量造成的迁移效果可以忽略。但导体的电导率远大于介质的电导率,使得导体中的电荷迁移平衡时间远小于介质中的电荷迁移平衡时间[12]。因此,在进行仿真分析时,选定的时间刻度主要针对于介质材料,认为导体内电荷迁移已近似达到平衡,于是近似有:
| $ {{J}_{0}}+gE=0 $ | (11) |
因而导体内的电场为:
| $ E\left(x \right)=-\frac{1}{g}{{J}_{0}}\left(x \right) $ | (12) |
可以看出,由于导体的电导率很大,所以导体中的电场强度远小于介质中的电场强度。
根据上面的分析,对于有导体的情况,在计算时可以近似认为导体两侧的介质对于电荷迁移是相通的,但不同之处在于高能电子在导体处的电荷沉积需要计入对应位置的介质层。于是在计算时可以把金属层压缩掉变成纯介质层,只是在压缩的位置处增加一定量的高能电子电荷沉积,然后再根据介质层中的电荷迁移算法计算出电荷迁移效应。
2 仿真结果与分析介质中金属层层数和厚度会影响电荷沉积特性,因此在分析过程中,首先根据铜板的不同厚度以及层数,设计了金属层厚度为0.3 μm、3 μm、9μm、15 μm、100 μm,以及金属层层数为6、8、12的平板型结构。然后计算了不同能量的电子辐照下,金属层层数和金属层厚度对电荷沉积的影响。
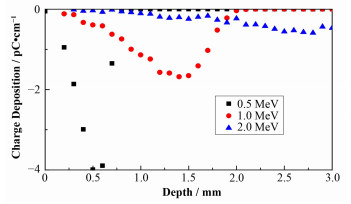
2.1 纯介质的电荷沉积首先针对没有金属层掺杂的FR4介质,仿真分析了0.5 MeV、1.0 MeV和2.0 MeV电子在介质中的沉积过程,如图 2所示。
|
图 2 不同能量电子在纯介质内的电荷分布 Figure 2 Charge deposition of electron in pure dielectric. |
从图 2中可看出,电荷密度峰值随入射电子能量增大而向介质更深处推移,这一现象与射程理论吻合。另外,由电子射程Webber公式计算得到的0.5 MeV、1.0 MeV、2.0 MeV能量电子辐照FR4时最大射程分别为0.94 mm、2.33 mm、5.31 mm。从图 2中还可以看出,模拟的结果与Weber经验公式的计算结果有比较好的吻合。
2.2 金属层层数对电荷沉积的影响金属层直接影响电子的穿透深度,从而影响电荷沉积密度,为此分别在0.5 MeV、1.0 MeV和2.0MeV电子辐照下,分析了6、8、12层金属层对电荷沉积过程的影响,如图 3-5所示。
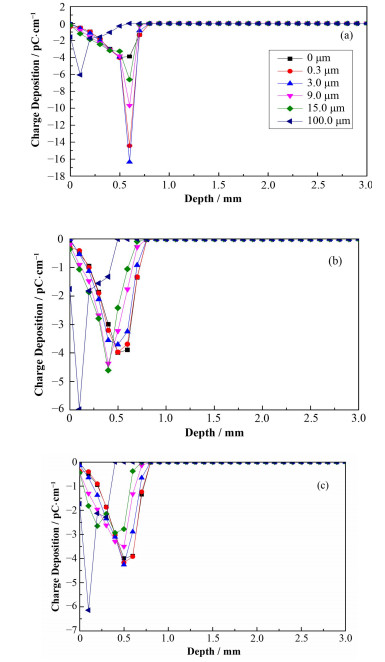
|
图 3 0.5 MeV辐照时不同金属层数的介质电荷沉积 (a) 0.5 MeV 6层,(b) 0.5 MeV 8层,(c) 0.5 MeV 12层 Figure 3 Charge deposition of electron in dielectric with different layers metal under 0.5 MeV. (a) 0.5 MeV 6 layers, (b) 0.5 MeV 8 layers, (c) 0.5 MeV 12 layers |
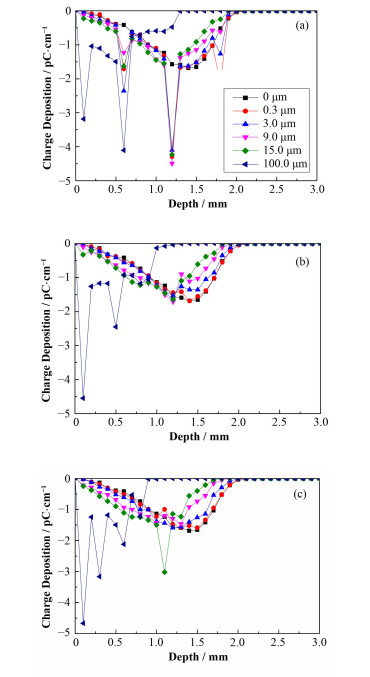
|
图 4 1.0 MeV辐照时不同金属层数的介质电荷沉积 (a) 1.0 MeV 6层,(b) 1.0 MeV 8层,(c) 1.0 MeV 12层 Figure 4 Charge deposition of electron in dielectric with different layers metal under 1.0 MeV. (a) 1.0 MeV 6 layers, (b) 1.0 MeV 8 layers, (c) 1.0 MeV 12 layers |
|
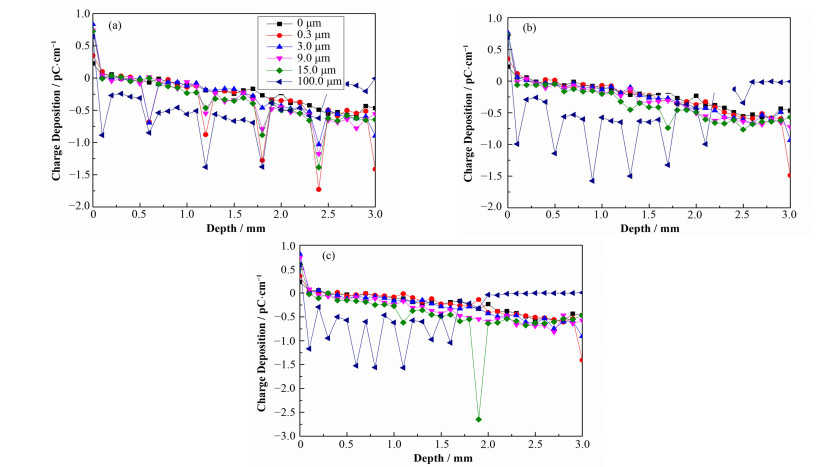
图 5 2.0 MeV辐照时不同金属层数的介质电荷沉积 (a) 2.0 MeV 6层,(b) 2.0 MeV 8层,(c) 2.0 MeV 12层 Figure 5 Charge deposition of electron in dielectric with different layers metal under 2.0 MeV. (a) 2.0 MeV 6 layers, (b) 2.0 MeV 8 layers, (c) 2.0 MeV 12 layers |
图 3是6层金属层在电子辐照下介质中电荷沉积分布,与纯介质中电荷沉积分布相比,0.5 MeV电子辐照时的电荷沉积密度出现了明显的前移,这是由于低能量电子的穿透能力较弱引起的。图 4、5分别是8层和12层金属层下的电荷沉积分布。金属层越多,由于对电子穿透的阻碍,使得与纯介质中电荷沉积分布特性相差越大。
从图 3-5中可以看出,电荷密度随深度的增加先增大后减小;同一深度处,沉积电荷随时间而增多,且随着时间增加,泄漏电流不断增大。另外,在有金属层的情况下,电荷会严重倾向于在金属层附近沉积,这是由于铜金属层的密度数倍于FR4的密度。由于电荷倾向于在金属层中沉积,使得FR4中的电荷沉积深度总体呈现出变浅的现象。
2.3 金属层厚度对电荷沉积的影响为更详尽分析金属层厚度对电荷沉积的影响,分别对0.3 μm、3 μm、9 μm、15 μm、100 μm厚金属层进行了仿真分析,得到其对沉积电荷的影响结果,如图 6所示。
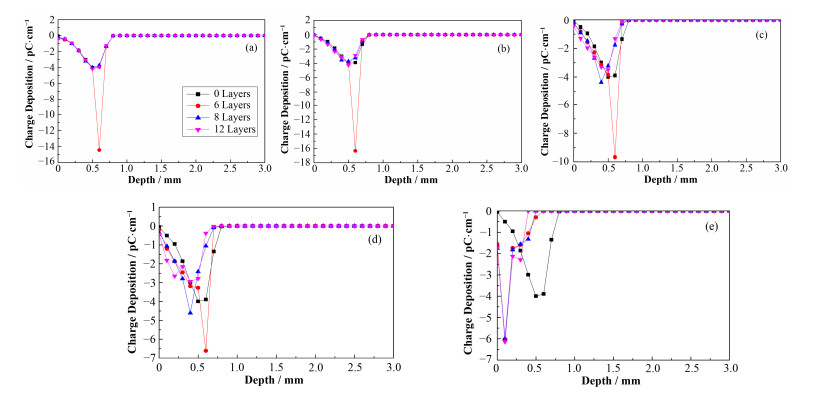
|
图 6 金属层厚度不同时得到的电荷分布结果 (a) 0.5 MeV 0.3 μm,(b) 0.5 MeV 3 μm,(c) 0.5 MeV 9 μm,(d) 0.5 MeV 15 μm,(e) 0.5 MeV 100 μm Figure 6 Charge deposition of electron in dielectric for metal of different layers. (a) 0.5 MeV 0.3 μm, (b) 0.5 MeV 3 μm, (c) 0.5 MeV 9 μm, (d) 0.5 MeV 15 μm, (e) 0.5 MeV 100 μm |
从图 6的仿真结果可以看出:(1)金属层厚度为0.3 μm、3 μm时,金属层层数不同时所获得的电荷分布曲线极为接近;(2)金属层厚度为9 μm时,6、8和12层金属层时所获得的电荷分布曲线略有差异;(3)金属层厚度为15 μm时,金属层层数不同时所获得的电荷分布曲线差异较大;(4)金属层厚度为100 μm时,增加金属层厚度时,电荷分布曲线差异极大。
3 结语通过建立平板型多层结构的物理模型,讨论分析了不同能量(0.5-2.0 MeV)电子辐射下,星用FR4介质材料的深层充电特性。分析表明:
1)不同能量的电子(0.5-2.0 MeV)辐射下,材料内部最大电荷沉积密度在介质材料中的深度随着能量而增加。
2)金属层层数越多,对电荷沉积影响越大,而金属层层数越少,又无法充分表征介质内部的电荷沉积特性,因此,8层金属层最能体现介质中电荷的特性。
3)金属层厚度越薄,则电荷沉积曲线与纯介质内电荷沉积曲线相似度越高。对于0.3 μm的金属层,由于其层厚度非常小,所以对FR4中的电荷沉积可以认为几乎无影响,但随着金属层厚度加深,其对FR4中的电荷沉积影响越来越剧烈。当金属层厚度达到100 μm时已经完全破坏FR4中的电荷沉积分布。
| [1] |
全荣辉.航天器介质深层充放电特征及其影响[D].北京:中国科学院研究生院, 2009
QUAN Ronghui.Characteristics and effects of deep space charge and discharge in spacecraft[D].Beijing:Graduate University of Chinese Academy of Sciences, 2009 http://cdmd.cnki.com.cn/Article/CDMD-80073-2009223010.htm |
| [2] |
秦晓刚, 贺德衍, 王骥. 行星际空间质子引起介质深层充电的GEANT4模拟研究[J].
宇航学报
, 2010, 31(2): 526–529.
QIN Xiaogang, HE Deyan, WANG Ji. GEANT4 simulation of interplanetary proton induced deep dielectrics charging[J]. Journal of Astronautics, 2010, 31(2): 526–529. DOI: 10.1007/978-3-642-30229-9_37 |
| [3] | Sessler G M, Figueiredo M T, Ferreira G F L. Models of charge transport in electron-beam irradiated insulators[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2004, 11(2): 192–202. DOI: 10.1109/TDEI.2004.1285887 |
| [4] | Noskov M D, Malinovski A S, Cooke C M, et al. Experimental study and simulation of space charge stimulated discharge[J]. Application Physics, 2002, 92(9): 4926–4934. DOI: 10.1063/1.1506395 |
| [5] | Min D M, Cho M, Khan A R. Surface and volume charge transport properties of polyimide revealed by surface potential decay with genetic algorithm[J]. IEEE Transactions on Di-electrics and Electrical Insulation, 2012, 19(2): 600–608. DOI: 10.1109/TDEI.2012.6180255 |
| [6] |
张振龙, 全荣辉, 韩建伟, 等. 卫星部件内部充放电试验与仿真[J].
原子能科学技术
, 2010, 44(9): 538–544.
ZHANG Zhenlong, QUAN Ronghui, HAN Jianwei, et al. Test and simulation of internal charging and discharging for satellite components[J]. Atomic Energy Science and Technology, 2010, 44(9): 538–544. |
| [7] | Wousik Kim. Internal electrostatic discharge monitor (IESDM)[J]. IEEE, 2010, 57(6): 126–138. |
| [8] | Mulville D R.NASA-HDBK-4002 avoiding problems caused by spacecraft on-orbit internal charging effects[S].Alabama:NASA, 1999 |
| [9] |
黄建国, 陈东. 卫星介质深层充电的计算机模拟研究[J].
地球物理学报
, 2004, 47(3): 392–397.
HUANG Jianguo, CHEN Dong. A study of deep dielectric charging on satellites by computer simulation[J]. Chinese Journal of Geophysics, 2004, 47(3): 392–397. DOI: 10.1002/cjg2.505 |
| [10] |
刘合凡, 葛良全, 谢希成, 等. 基于蒙特卡罗方法的XRF探测器立体角分析[J].
核技术
, 2015, 39(6): 060502.
LIU Hefan, GE Liangquan, XIE Xicheng, et al. Analysis of XRF solid angle detector based on Monte Carlo methods[J]. Nuclear Techniques, 2015, 39(6): 060502. DOI: 10.11889/j.0253-3219.2015.hjs.38.060502 |
| [11] |
乌江, 白婧婧, 沈宾, 等. 航天器介质内电场形成机理与防护方法分析[J].
导弹与航天运载技术
, 2009, 5: 13–17.
WU Jiang, BAI Qingqing, SHEN Bin, et al. Study on formation mechanism of inner electric field in dielectric of spacecraft and protection methods[J]. Missile and Space Vehicle, 2009, 5: 13–17. |
| [12] | European Cooperation for Space Standardization.ECSS-E-ST-20-06C spacecraft charging[S].Netherlands:ESA Requirements and Standards Division, 2008 |
