裂变电离室的内部涂有一层裂变材料并充以不同的可电离的气体,由中子和裂变材料发生核反应产生的裂变碎片引起内部气体电离,正负离子在电场作用下,给出电信号,从而达到测量中子的目的。由于外加电场的电压不同,所形成的电信号特性不同。对于电离室,其输出的电流信号随电压变化的曲线有三个典型的特征区域,分别为:复合区、饱和区以及雪崩区[1]。其中,裂变电离室工作在饱和区,饱和区的电压范围越大,探测器的性能越好,而电离气体的复合速率系数和电离系数的增加会使复合区和雪崩区更加明显,相应地,饱和区电压范围就会变小。
影响复合速率系数和电离系数的因素有很多,如气体成分、温度、外加电场以及电离度等。除了气体的影响外,探测器的阴极、阳极尺寸和灵敏区长度也对饱和区范围有影响。微型裂变电离室通常应用于反应堆堆芯区域,即中子通量密度和温度很高的环境中,又因为其尺寸小,因此对这些参数更加敏感。本文在已有工作[1-6]的基础上,借助最新版本的BOLSIG+(03/2016)[7-8],重新评估了这些参数对电流模式下裂变电离室的影响,并对研究方法和研究内容进行了一定的改进和补充。BOLSIG是一款数值求解电子波尔兹曼方程的免费程序,适用于计算在均匀电场中弱电离气体的各种基本系数和截面数据。
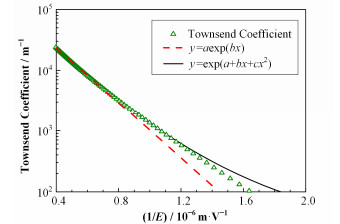
1 计算与分析计算中需要用到的一个关键参数为Townsend第一电离系数(Townsend first ionization coefficient),它的定义是沿电场方向,在单位长度上由电子碰撞产生的平均电离数。对于该系数的拟合,拟合形式不能过于复杂,否则在后续的计算中难以求解。根据文献[2],如果以横坐标x表示电场强度的倒数1/E,m ·V-1,以纵坐标y表示Townsend系数α,m-1,那么在只考虑一个大气压的情况下,采用的拟合形式为y=aexp (bx),式中:a和b为拟合系数。该表达式简单,便于后续计算,但在考虑电离度的影响后,对于电场强度较小时的拟合结果很不理想。如果采用y=exp (a+bx+cx2)的形式进行拟合,可以改善这种情况,并且易于计算,式中:c为拟合系数。当电离度为10-7时,两种方法拟合结果的对比如图 1所示。
|
图 1 Townsend系数的两种拟合结果对比 Figure 1 Comparison of two methods in fitting of the Townsend coefficients. |
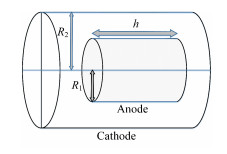
为了简化计算,本文只考虑最简单的同轴型探测器结构,图 2为同轴型裂变电离室的基本结构。其中:R1为阳极半径;R2为阴极半径;h为灵敏区长度。
|
图 2 同轴型探测器基本结构示意图 Figure 2 Diagram of the basic structure of coaxial type detector. |
根据文献[2]以及上述讨论的另一种拟合方法,可以得到裂变电离室在饱和区的最小电压Vmin、最大电压Vmax和饱和电流Isat的表达式:
| $ \begin{align} &{{V}_{\text{min}}}\approx 0.5\times \text{(}1+\varepsilon \text{(}{{\lambda }_{\text{e}}}, {{\lambda }_{\text{a}}}\text{))}\times \\ &\quad \quad \ \, \text{ln}\left({{R}_{2}}/{{R}_{1}} \right)\sqrt{k{{I}_{\text{sat}}}\text{(}R_{2}^{2}-R_{1}^{2}\text{)}/{{\mu }_{\text{e}}}{{\mu }_{\text{a}}}eh} \\ \end{align} $ | (1) |
| $ \begin{align} &{{V}_{\max }}\approx 2c({{R}_{2}}-{{R}_{1}})/\\ &\quad \quad \ \left[-b-\sqrt{{{b}^{2}}-4c(a+\ln({{R}_{2}}-{{R}_{1}})+2.323)} \right] \\ \end{align} $ | (2) |
| $ {{I}_{\text{sat}}}=e{{\tau }_{\text{f}}}{{X}_{0}}[{{R}_{2}}\times E\left({{R}_{1}}/{{R}_{2}} \right)-{{R}_{1}}] $ | (3) |
式中:λe、λa分别为填充气体的电子和离子的郎之万因子;ε为λe和λa的函数;k为气体中离子与电子的复合速率系数;e为元电荷;τf为裂变率;X0为气体单位长度径迹内裂变产物产生的电子-离子对的平均数,对于微型裂变电离室,可以近似认为X0是一个常数;E为第二类完全椭圆积分;μe、μa分别为电子和离子迁移率;a、b、c是通过对Townsend电离系数拟合得到的参数。
定义探测器的饱和区电压范围:
| $ L={{V}_{\text{max}}}-{{V}_{\text{min}}} $ | (4) |
该值越大,则探测器性能越好。
根据文献[1],对于Ar气300K环境下的k为:
| $ k=8.8\times {{10}^{-4}}\sqrt{P}\times 4\pi {{\mu }_{\text{e}}}(E)e/{{\varepsilon }_{0}}{{\varepsilon }_{\text{r}}} $ | (5) |
表 1给出了不同条件下的拟合参数。
| 表 1 不同条件下的拟合参数 Table 1 Fitting parameters under different conditions. |
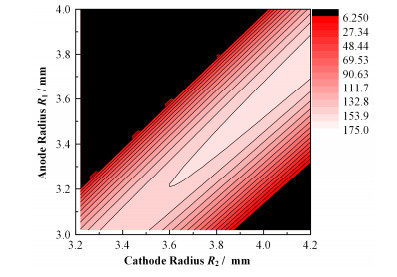
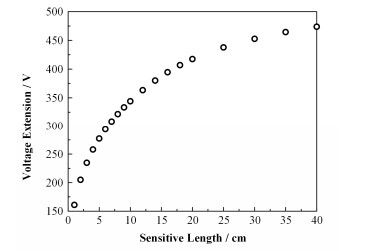
假设气体为Ar气,电离度为10-7,温度为300K,气压为105Pa,则饱和区电压范围L的分布如图 3所示。图 3中横坐标表示阴极半径,纵坐标表示阳极半径,不同L在图 3中用颜色的深浅区分。从图 3可见,L较大的区域,其阴极半径与阳极半径之差△R约为0.4 mm。当△R太大或太小时,L都会变得很小。此外,计算结果(图 4)表明,L随灵敏区长度h而增加,但曲线呈收敛趋势,说明h增加到一定程度后,L不会再有明显变化。
|
图 3 300K、105Pa氩气环境下饱和区电压范围随阴极、阳极半径的分布 Figure 3 Change in voltage extension as a function of radius of anode and cathode in 300K, 105Pa and argon environment. |
|
图 4 300K、105Pa氩气环境下饱和区电压范围与灵敏区长度的关系 Figure 4 Change in voltage range of saturation zone as a function of sensitive length in 300K, 105Pa and argon environment. |
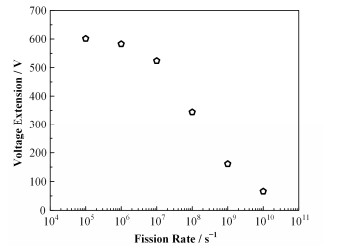
在其他参数不变的情况下,考虑裂变率对探测器的影响,计算结果如图 5所示。从图 5可以看到,裂变率增加会导致饱和区电压范围的下降。也就是说,在中子通量密度很高或者探测器内转换材料很多的情况下,探测器的性能会有明显的下降。
|
图 5 300K、105Pa氩气环境下饱和区电压范围与裂变率的关系 Figure 5 Change in voltage extension as a function of fission rate in 300 K, 105Pa and argon environment. |
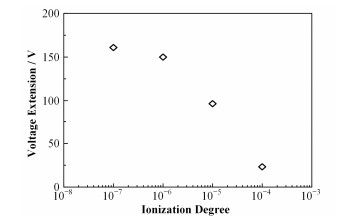
图 6考察了探测器在其它参数不变的情况下,电离度变化带来的性能变化。当电离度达到10-5时,饱和区电压范围出现了明显的降低。裂变率的增加会导致电离度的增加,考虑到裂变率和电离度的双重影响,实际的电压范围下降会更加显著。除了裂变率导致电离度增加外,温度可能是导致电离度增加的另一因素。在电子和离子的复合过程中,电子可能处于气体原子的高里德堡态[9]。根据美国国家标准与技术研究院(National Institute of Standards and Technology, NIST)的数据,以Ar原子3s23p5(2P1/2)7f态为例,处于该能级的电子电离需要约0.1eV的能量。如果不考虑外加电场,根据经典热力学估算,300K温度下自由电子的平均动能约为0.0388eV,这个能量不足以电离3s23p5(2P1/2)7f能级的电子,而当温度增加到1000K时,自由电子的平均动能约为0.1293eV,这一能量就可以将3s23p5(2P1/2)7f能级以上的电子电离。从以上分析中至少可以得出一个结论,在温度高时,电子更容易被电离,电离度也会随之增加。但这是否是高温下电离度增加的主要原因,还需要更细致的理论分析和实验验证。
|
图 6 300 K、105Pa氩气环境下饱和区电压范围与电离度的关系 Figure 6 Change in voltage extension as a function of ionization degree in 300K, 105Pa and argon environment. |
对文献中关于Townsend系数的拟合方式进行了改进,计算了裂变电离室各个参数对饱和区电压范围的影响,得到以下结论:增加灵敏区长度可以有效地增加探测器的饱和区电压范围,但曲线呈收敛趋势,过长的灵敏区并不能带来更好的性能。裂变率的增加会显著降低探测器的电压范围,说明在高中子通量密度或探测器转换材料太多的情况下,探测器的性能会明显变差。电离度升高会显著降低探测器的电压范围。增加电离度的一个重要原因是裂变率增加导致空间电荷效应;另外一个可能的原因是辐射复合产生高里德堡态布居,而温度升高时处于高里德堡态的电子更容易被电离,进一步增加电离度。
通过这些计算和分析,希望能为裂变电离室的研发和设计工作提供一些思路和数据参考。
| [1] | Chabod S, Fioni G, Letourneau A, et al. Modelling of fission chambers in current mode-analytical approach[J]. Nuclear Instruments and Methods in Physics Research Section A, 2006, 566(2): 633–653. DOI: 10.1016/j.nima.2006.06.067 |
| [2] | Chabod S, Letourneau A.Improvements in the modelling of micro fission chambers operated in current mode[C].ANIMMA International Conference, Marseille, France, 2009.DOI:10.1109/ANIMMA.2009.5503675 |
| [3] | Chabod S. Impact of space charges on the saturation curves of ionization chambers[J]. Nuclear Instruments and Methods in Physics Research Section A, 2009, 602(2): 574–580. DOI: 10.1016/j.nima.2009.01.018 |
| [4] | Chabod S. Saturation current of miniaturized fission chambers[J]. Nuclear Instruments and Methods in Physics Research Section A, 2009, 598(2): 578–590. DOI: 10.1016/j.nima.2008.09.051 |
| [5] | Chabod S. A perturbation method to examine the steady-state charge transport in the recombination and saturation regimes of ionization chambers[J]. Nuclear Instruments and Methods in Physics Research Section A, 2008, 595(2): 419–425. DOI: 10.1016/j.nima.2008.07.115 |
| [6] | Chabod S. Charge collection efficiency in ionization chambers operating in the recombination and saturation regimes[J]. Nuclear Instruments and Methods in Physics Research Section A, 2009, 604(3): 632–639. DOI: 10.1016/j.nima.2009.03.019 |
| [7] | Hagelaar G J M, Pitchford L C. Solving the Boltzmann equation to obtain electron transport coefficients and rate coefficients for fluid models[J]. Plasma Sources Science and Technology, 2005, 14(4): 722–733. DOI: 10.1088/0963-0252/14/4/011 |
| [8] | Hagelaar G J M. Coulomb collisions in the Boltzmann equation for electrons in low-temperature gas discharge plasmas[J]. Plasma Sources Science and Technology, 2016, 25(1): 015015. DOI: 10.1088/0963-0252/25/1/015015 |
| [9] | Li C Y, Qu Y Z, Wang J G. State-selective radiative recombination cross sections of argon ions[J]. Journal of Quantitative Spectroscopy and Radiative Transfer, 2012, 113(15): 1920–1927. DOI: 10.1016/j.jqsrt.2012.05.005 |
