2. 东华理工大学 核科学与工程学院 南昌 330013;
3. 成都理工大学 成都 610059
2. School of Nuclear Science and Engineering, East China University of Technology, Nanchang 330013, China;
3. Chengdu University of Technology, Chengdu 610059, China
航空γ能谱探测的实质是将航空飞行器作为运载工具,装载具备相应探测效率的γ能谱仪对环境γ辐射进行监测。近年来,国内外专家已将其作为核事故应急监测和寻找丢失的强放射源的有效手段[1-6],且在我国《国家核应急计划》中明确规定“航空测量是核应急辐射监测中的一个重要手段,一旦需要时紧急调用,实施快速、高效和大面积的应急监测”[7]。目前航空γ场理论是建立在点探测器的基础上[6],未考虑探测设备本身的几何形状及材质的影响,仅能运用于相对规律的研究,须先建立起基准刻度模型。但大量人工核素的半衰期都较短,不可能都制作成面源用于刻度[7](如我国仅制作了边长为1 m的正六边形137Cs和60Co刻度模型各一块[8])。怎样才能给出更加精确的定量结果是急需解决的问题[9],关键在于有效获得感兴趣放射性核素的航空γ能谱仪全能峰探测效率值。
根据微积分思想,在网格划分足够精细的情况下,任意形状人工辐射源的航空γ能谱仪全能峰探测效率等于所划分的各“微体积源”对应探测效率之和。此时,“微体积源”可近似为特征γ射线均从中心位置发射的点源,所以解决上述问题的核心在于建立任意位置点源的航空γ能谱仪全能峰探测效率计算方法。Grasty等[5]实验发现,在单根晶体的航空γ能谱仪中心外同一圆环面上移动γ辐射源,全能峰探测效率与偏移垂直方向的夹角余弦值成线性函数关系,并基于此线性规律和航空γ场理论给出了地表面任意位置点源的航空γ能谱仪全能峰探测效率值的计算公式。这也是点源代替体源进行航空γ能谱仪刻度的基础,近年来刘新华[3]和胡明考[8]的研究小组也相继开展了相应的研究,发现该模型的缺点在于点源位置摆放差异对结果的影响较大、工作量繁重以及对工作人员造成较大的辐射危害。
在γ能谱分析领域Monte Carlo模拟软件在近距离探测时效率刻度的可靠性已广泛被实验验证[10]。但在约100 m远的距离探测时,由于模拟粒子进入探测器的概率过低导致结果偏离真实。而目前商业化的无源效率刻度软件仅可用于圆柱体探测器[11],无法计算装载长方体型探测器的航空γ能谱仪。
针对上述问题,本文在考虑航空γ能谱仪探测器的尺寸(长方体)和材质等因素影响的基础上,建立一套航空γ能谱仪全能峰探测效率无源刻度数值计算模型,并对其可靠性进行验证。
1 点源探测效率数值计算模型的建立目前航空γ能谱探测单元多为装载长方体(长a=40.64 cm、宽b=10.16 cm、高c=10.16 cm)型NaI (Tl)晶体,如图 1(a)中长方体ABCDEFGH(中心为坐标轴X'Y'Z'的原点O')所示。因长方体沿中心坐标轴及对角线(沿CH线和DG线)对称,所以公式推导仅需考虑点源P坐标满足Z'≥0、X'≥Y'/cos (45°)≥0的情形。在上述情况下,点源P发射的特征γ射线可能从顶面CDHG、侧面EFHG和ADHF进入图 1(a)中NaI (Tl)晶体(P点距上述三个面的垂直距离分别为d、k和j)。

|
图 1 单晶体航空γ能谱仪外任意位置点源的全能峰探测效率计算示意图 (a)从顶面CDHG进入探测器,(b)从左侧面EFHG进入探测器,(c)从前侧面ADHF进入探测器 Figure 1 Schematic view of one detector of AGS irradiated by a point source placed at arbitrary position. (a) Top-surface CDHG, (b) Left facet EFHG, (c) Front ADHF |
假设从P点出射的γ射线与PW线成θ角,其在CDHG面上的投影线与CD线的夹角为ϕ。倘若该γ射线从顶面HGH'入射,此时ϕ∈[∠GTU, ∠HTU]。此时∠GTU=ϕ1=arctan[k/(b+j)],∠HTU=ϕ2=arctan (k/j)。
而在每一个ϕ方向上,当入射方向与HG线有交点时,θ角取最小值θ1=arctan[k/(d·sinϕ)],当入射方向与CG线有交点时,θ角取最大值θ2=arctan[(b+j)/(d·cosϕ)];入射方向与BE线相交为该γ射线是从底面ABEF还是侧面BCGE出射的判据,此时θ3=arctan{(b+j)/[(c+d)·cosϕ)]}。
在j≤b·d/c时,θ1 < θ3≤θ2,ϕ≤ϕ3=arctan{k·(c+d)/[d·(b+j)]}。说明ϕ∈[ϕ1, ϕ3]时所有进入NaI (Tl)晶体后未与其发生相互作用的入射γ射线均从侧面BCGE(在NaI (Tl)晶体内的衰减长度为l1=(b+j)/(sinθ·cosϕ)-d/cosθ)出射;而ϕ∈[ϕ3, ϕ2]时,当入射角为θ∈[θ1, θ3]的γ射线均从底面ABEF(在NaI (Tl)晶体内的衰减长度为l2=c/cosθ)出射,同时入射角为θ∈[θ3, θ2]的γ射线均从侧面BCGE出射。在j > b·d/c时,θ1 < θ2≤θ3。说明ϕ∈[ϕ1, ϕ2]所有进入NaI (Tl)晶体后未与其发生相互作用的入射γ射线均从侧面BCGE出射。根据上述分析可知,从顶面HGH'入射γ射线的全能峰探测效率计算公式η1为:
| $ \begin{array}{l} {\eta _1} = \\ \frac{1}{{4\pi }}\left\{ {\begin{array}{*{20}{c}} \begin{array}{l} \int_{{\phi _1}}^{{\phi _3}} {\int_{{\theta _1}}^{{\theta _2}} {f \cdot \left( {1 - {e^{ - {\mu _1}{l_1}}}} \right)sin\theta d\theta } d\phi } + \\ \int_{{\phi _3}}^{{\phi _2}} {\left[ {\int_{{\theta _1}}^{{\theta _3}} {f \cdot \left( {1 - {e^{ - {\mu _1}{l_2}}}} \right)sin\theta d\theta } + \int_{{\theta _3}}^{{\theta _2}} {f \cdot \left( {1 - {e^{ - {\mu _1}{l_1}}}} \right)sin\theta d\theta } } \right]d\phi \;\;\;\;j \le \frac{{b \cdot d}}{c}} \end{array}&{}\\ {\int_{{\phi _1}}^{{\phi _2}} {\int_{{\theta _1}}^{{\theta _2}} {f \cdot \left( {1 - {e^{ - {\mu _1}{l_1}}}} \right)sin\theta d\theta } d\phi \;\;\;\;\;\;j > \frac{{b \cdot d}}{c}} }&{} \end{array}} \right. \end{array} $ | (1) |
式中:μ1为γ射线在NaI (Tl)晶体中的光电效应线衰减系数(源自文献[12]所述XCOM软件);f为γ射线到达NaI (Tl)晶体前的衰减规律(在同一材料内的连续路径上服从指数衰变规律[5-6]),如点源在土壤内埋深为L、NaI (Tl)晶体上有厚为h的屏蔽层时f=exp{-[μ2·(d-h-L)+μ3·h+μ4·L]/cosθ},此时μ2为γ射线在空气中的总线衰减系数,μ3为γ射线在NaI (Tl)晶体外屏蔽层中的总线衰减系数,μ4为γ射线在土壤中的总线衰减系数。
依据上述推导方法,同理可得到γ射线从顶面H'HC'C和CC'D入射时的全能峰探测效率计算公式η2和η3分别如下:
| $ {\eta _2}=\frac{1}{{4\pi }}\left\{ {\begin{array}{*{20}{c}} {\int_{{\phi _2}}^{{\phi _4}} {\left[{\int_{{\theta _4}}^{{\theta _3}} {f \cdot \left({1-{e^{-{\mu _1}{l_2}}}} \right)sin\theta d\theta }+\int_{{\theta _3}}^{{\theta _2}} {f \cdot \left({1-{e^{ - {\mu _1}{l_1}}}} \right)sin\theta d\theta } } \right]d\phi } }&{j \le \frac{{b \cdot d}}{c}}\\ {\int_{{\phi _2}}^{{\phi _4}} {\int_{{\theta _4}}^{{\theta _2}} {f \cdot \left({1 - {e^{ - {\mu _1}{l_1}}}} \right)sin\theta d\theta } d\phi } }&{j > \frac{{b \cdot d}}{c}} \end{array}} \right. $ | (2) |
| $ \begin{array}{l} {\eta _3} = \\ \frac{1}{{4\pi }}\left\{ {\begin{array}{*{20}{c}} \begin{array}{l} \int_{{\phi _5}}^{{\phi _6}} {\int_{{\theta _5}}^{{\theta _6}} {f \cdot \left( {1 - {e^{ - {\mu _1}{l_3}}}} \right)sin\theta d\theta } d\phi } + \\ \int_{{\phi _6}}^{\frac{\pi }{2} - {\phi _4}} {\left[ {\int_{{\theta _5}}^{{\theta _7}} {f \cdot \left( {1 - {e^{ - {\mu _1}{l_2}}}} \right)sin\theta d\theta } + \int_{{\theta _7}}^{{\theta _6}} {f \cdot \left( {1 - {e^{ - {\mu _1}{l_3}}}} \right)sin\theta d\theta } } \right]d\phi \;\;\;j \le \frac{{b \cdot d}}{c}} \end{array}&{}\\ {\int_{{\phi _5}}^{\frac{\pi }{2} - {\phi _4}} {\int_{{\theta _5}}^{{\theta _6}} {f \cdot \left( {1 - {e^{ - {\mu _1}{l_3}}}} \right)sin\theta d\theta } d\phi \;\;\;j > \frac{{b \cdot d}}{c}} }&{} \end{array}} \right. \end{array} $ | (3) |
式中:ϕ4=arctan[(a+k)/(b+j)];ϕ5=arctan[j/(a+k)];ϕ6=arctan{[j·(c+d)]/[d·(a+k)]};θ4=arctan[j/(d·cosϕ)];θ5=arctan[j/(d·sinϕ)];θ6=arctan[(a+k)/(d·cosϕ)];θ7=arctan {(a+k)/[(c+d)·cosϕ]};l3=(a+k)/(cosϕ·sinθ)-d/cosθ。根据上述推导可知,点源P出射的γ射线从顶面CDHG进入探测器的全能峰探测效率公式为:
| $ {\eta ^T}\left({a, b, c, d, k, j} \right)={\eta _1}+{\eta _2}+{\eta _3} $ | (4) |
从图 1(b)与图 1(a)的比较发现,仅需将式(4)中参数a与c、k与d互换,即ηT(c, b, a, k, d, j)为点源P出射的γ射线从侧面EFHG进入探测器的全能峰探测效率公式;同理,图 1(c)也直观显示ηT(a, c, b, j, k, d)为点源P出射的γ射线从侧面ADHF进入探测器的全能峰探测效率公式。注意,如果点源在土壤中埋深L > 0,那么在上述变换前应将f函数改成f1=exp{-[μ2·(d-h-L/tanθ)+μ3·h]/cosθ+μ4·L/sinθ}。
综上所述,任意位置点源P发射的特征γ射线在航空γ能谱探测单元内全能峰探测效率数值计算公式为:
| $ \begin{array}{l} \eta \left({a, b, c, d, k, j} \right)={\eta ^T}\left({a, b, c, d, k, j} \right)+{\eta ^T}\left({c, b, a, k, d, j} \right)+\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;{\eta ^T}\left({a, c, b, j, k, d} \right) \end{array} $ | (5) |
对式(5)而言,远距离探测与近距离探测的不同点在于μ2是否准确可行。而近距离探测实验需验证在不同立体角(真空环境下,源发射的γ射线进入探测器的几率)下计算结果是否准确。
2.1 不同立体角下计算结果可靠性验证实验采用课题组自制的AGS-863型航空γ能谱仪(单箱晶体内下视探测阵列由4个平行排布的探测单元组成),现场布置如图 2所示。以下视探测阵列NaI (Tl)晶体中心为原点O(在墙面上的投影为Q)、横切面为XOY面,墙面为PTQ面。并假设点源P和O点的连线与Z轴夹角为τ、其在XOY面上的投影线OT与Y轴夹角为φ。

|
图 2 AGS-863型航空γ谱仪单箱晶体的137Cs点源全能峰探测效率实测现场布置示意图 Figure 2 Experimental arrangements for full-energy peak efficiency in one box of AGS-863 irradiated by a point source of 137Cs. |
首先将下视探测阵列按右侧面平行于墙面(如图 2摆放)、OQ=100 cm固定,将活度A0=8.78×105Bq的137Cs源用胶带纸贴在墙壁上P点。获得P点在TQ线上(即τ=90°)、PQ分别为0 cm、10 cm、20 cm、40 cm、60 cm、90 cm、120 cm、150 cm、200 cm、250 cm和300 cm时下视探测阵列在t=120 s内的累积γ能谱。采用高斯函数Levenberg-Marquardt拟合算法[13]提取特征γ射线峰的净面积,反算得到下视探测阵列对137Cs的661.657 keV特征γ射线全能峰探测效率随φ变化如图 3(a)所示。其次,维持X轴不变,将下视探测阵列逆时针旋转90°,依然在上述点位放置137Cs源进行120 s测量,相当于在原始坐标下φ=0°、改变τ时全能峰探测效率变化规律,实验结果如图 3(b)所示。可以看出,在φ和τ仅一个量改变时引起的立体角变化下,航空γ能谱仪全能峰探测效率实验值与上述数值模型计算结果均在±5%的相对偏差范围以内,初步证实上述方案适用于不同立体角下点源全能峰探测效率的计算。

|
图 3 AGS-863型航空γ谱仪单箱晶体的137Cs点源全能峰探测效率结果比对 (a)下视探测阵列右侧面平行于墙面,(b)下视探测阵列顶面平行于墙面 Figure 3 Full-energy peak efficiencies in one box of AGS-863 irradiated by a point source of 137Cs. (a) The wall surface parallel to the right side of the downward-looking detectors, (b) The wall surface parallel to the top of the downward-looking detectors |
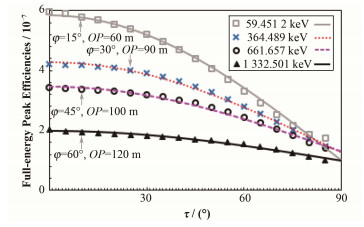
最后计算单箱晶体的航空γ能谱仪外不同OP、φ和τ值下构成的圆环面上点源全能峰探测效率,结果如图 4所示。Grasty等[5]认为在OP和φ不变时,不同τ下全能峰探测效率值ητ的变化规律如下:
| $ {\eta _\tau }={\eta _0} \cdot [p \cdot cos(\tau)+q] $ | (6) |
|
图 4 航空γ谱仪单箱晶体的全能峰探测效率变化规律 Figure 4 Change rules of full-energy peak efficiencies in one box of AGS irradiated by a point source. |
式中:η0为τ=0°时的全能峰探测效率值;p和q为待拟合参数。采用式(6)对图 4数据点进行拟合发现拟合优度均在0.992以上,充分说明上述方案能可靠应用于计算不同立体角下点源的航空γ能谱仪全能峰探测效率。
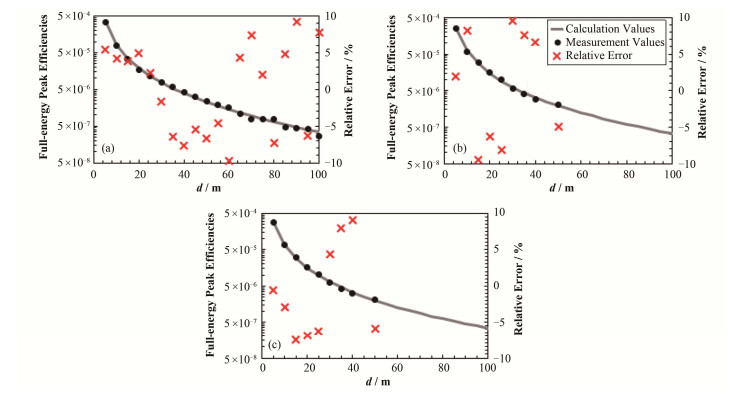
2.2 μ2准确性验证在一处约500 m×500 m的平整地面上,将装载单箱晶体的航空γ能谱仪悬挂在两个氢气艇连杆之下,通过控制自带长度刻度绳索收放来调节航空γ能谱仪的探测高度d(实验时d取5-100 m、间隔5m)。实验中固定航空γ能谱仪在地面上的投影点,并在其中心分别摆放点源137Cs(活度为2.588×109Bq)和60Co(活度为1×108 Bq),并利用§2.1所述方法计算得到点源正上方不同探测高度航空γ能谱仪全能峰探测效率,结果如图 5所示。看出在可探测范围内(源活度大于此时探测高度下的探测限),实验值与相应尺寸模型下的计算结果间相对偏差均在±10%以内,证明所采用的γ射线在空气中的总线衰减系数μ2是准确、可行的。充分说明前述计算方案适用于实际航空γ能谱测量飞行高度。
|
图 5 137Cs和60Co点源正上方不同探测高度AGS-863型航空γ谱仪单箱晶体全能峰探测效率结果比对 (a) 661.657 keV,(b) 1 173.237 keV,(c) 1 332.501 keV Figure 5 Full-energy peak efficiencies in one box of AGS-863 irradiated by directly below point source of 137Cs and 60Co. (a) 661.657 keV, (b) 1 173.237 keV, (c) 1 332.501 keV |
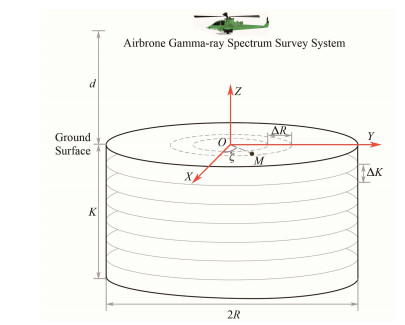
因γ射线与地层介质发生相互作用时射线强度按指数规律衰减,导致航空γ能谱探测深度约为地表层1.5 m[14]。假设有如图 6所示自地表向下深K、半径为R的放射性核素均匀分布圆柱体地层,地面上任意一点M和中心O连线MO与X轴间成ζ角。先在Z轴方向依间隔ΔK厚将其分成u=K/ΔK层;对每一层,以ΔR间隔化分成v=R/ΔR个圆环,对每一个圆环以Δζ度角为间隔均分成w=360/Δζ份,则上述圆柱体地层总共被划分成u·v·w份。
|
图 6 网格划分圆柱源示意图 Figure 6 Schematic view of cylinder source divided by a grid partition method. |
对第g层中m圆环(从中心往外数)内第n份(按角度从小到大数)“微体积源”来说,其中心点对应的式(5)中参数如下:
| $ \left\{ \begin{array}{l} {d_{g, m, n}}=d+L\\ {k_{g, m, n}}=\Delta R \cdot \left({m - 0.5} \right)\cdot \cos \left[{\Delta \varsigma \cdot \left({n-0.5} \right)} \right] - \frac{a}{2} - h\\ {j_{g, m, n}}=\Delta R \cdot \left({m - 0.5} \right)\cdot \sin \left[{\Delta \varsigma \cdot \left({n-0.5} \right)} \right] - \frac{b}{2} - h\\ {L_{g, m, n}}=\Delta K \cdot \left({g - 0.5} \right) \end{array} \right. $ | (7) |
联立式(5)与式(7)可得上述地层上d探测高空的航空γ能谱仪全能峰探测效率如下:
| $ \eta \left( K,R \right)={\left[ \sum\limits_{g=1}^{u}{\sum\limits_{m=1}^{v}{\sum\limits_{n=1}^{w}{\eta \left( a,b,c,{{d}_{g,m,n}},{{k}_{g,m,n}},{{j}_{g,m,n}} \right)\cdot {{N}_{g,m,n}}}}} \right]}/{{{N}_{K,R}}}\; $ | (8) |
式中:NK, R为上述地层单位时间发射待分析能量的特征γ射线总数目;Ng, m, n为上述地层中第g层中m圆环内第n份“微体积源”单位时间发射待分析能量的特征γ射线数目。
首先设计以下两个近距离探测模型来验证上述网格划分的可行性:1)K=50 cm、R=15 cm和d=300cm的放射性均匀分布圆面源;2)K=50 cm、R=250 cm和d=100 cm的圆柱体源(内部填充Beck土壤,化合物组成见文献[14])。探测设备采用装载单箱晶体的航空γ能谱仪,取ΔK=ΔR=1 cm、Δζ=5°网格化地层得到的计算结果如表 1所示,与MCNP5软件模拟结果(不确定度小于0.5%)的相对偏差均在±1.5%以内,证明上述计算模型适用于面源与体源上空航空γ能谱仪全能峰探测效率计算。
| 表 1 近距离探测时航空γ能谱仪全能峰探测效率结果比对 Table 1 Full-energy peak efficiencies of AGS near the no-point source. |
同时用上述模型计算含1 kBq·kg-1的40K(特征γ射线能量1 460.83 keV)或208Tl(特征γ射线能量2614.533 keV)、R=800 m和K=1.5 m的圆柱体地层(土壤成分见文献[15],可认为近似无限大地层[14])上空不同探测高度上的两箱晶体的航空γ能谱仪全能峰探测效率如表 2所示。可以看出计算结果均比在石家庄黄碧水库动态带(天然放射性核素分布较均匀,为我国航空γ能谱仪不同探测高度校正系数的刻度模型[16])陆地上空相应高度的300 s累积测量谱的分析结果高8.33%-15.82%,分析发现差异的主要原因在于上述模型未考虑实测过程中直升飞机底板材料对γ射线的衰减。而底板材料多采用复合材料,难以获得其元素组成及密度来计算它对γ射线的线衰减系数,在后续实践应用中可现场利用点源衰减实验获得。
| 表 2 无限大体源上90-150 m高空航空γ能谱仪全能峰探测效率结果比对 Table 2 Full-energy peak efficiencies of AGS 90-150 m away from infinite volume source. |
本文依据窄束γ射线的指数衰减规律,推导建立任意位置点源的航空γ能谱仪全能峰探测效率计算方法。不同立体角下探测的验证分析发现:单箱晶体的航空γ能谱仪底面及侧面外平行轴线上不同位置的137Cs点源全能峰探测效率计算值与实验值相对偏差均在±5%以内;不同半径(60-120 m)和角度的圆环面上多种核素点源的航空γ能谱仪全能峰探测效率变化规律与Grasty等[5]的实验规律一致。同时利用氢气球将单箱晶体的航空γ能谱仪升至5-100 m高空探测地面上的137Cs和60Co点源,结果证实上述数值解析方法可应用于实测高度中去。
采用微积分思想将任意形状的γ辐射源网格化成多个“微体积源”,利用点源计算模型得到各个“微体积源”的航空γ能谱仪全能峰探测效率值,通过叠加原理建立任意形状的γ辐射源上空航空γ能谱仪无源效率刻度计算模型。该模型在低空探测时的计算结果与MCNP5模拟结果在±1.5%的相对偏差范围内符合,而在90-150 m高空对1460.83 keV和2614.533 keV的γ射线计算结果与实测值相差8.33%-15.82%,说明本文所述的无源效率刻度方法可有效应用于航空γ能谱探测实践。为提高模型的精确度,在今后的实践中应提前测量各现场材料的线衰减系数,尤其是飞机底板。
致谢 感谢中国国土资源航空物探遥感中心的万建华高工提供的石家庄动态带实测航空γ能谱测量数据,感谢曾为该数据付出辛劳的全体成员。| [1] |
王南萍, 熊盛青, 周锡华, 等. 航空伽玛能谱仪对137Cs点源响应特征及全谱数据的提取技术[J].
核技术
, 2005, 28(4): 313–318.
WANG Nanping, XIONG Shengqing, ZHOU Xihua, et al. Spectra characteristics of airborne spectrometer to 137Cs sources and extraction of full abstraction peak[J]. Nuclear Techniques, 2005, 28(4): 313–318. |
| [2] |
邓磊, 杨亚新, 卢存恒, 等. 一种确定放射性烟羽边界的新方法[J].
核技术
, 2009, 32(12): 911–914.
DENG Lei, YANG Yaxin, LU Cunheng, et al. A new method for boundary determination of radioactive plume[J]. Nuclear Techniques, 2009, 32(12): 911–914. |
| [3] |
刘新华, 张永兴, 顾仁康, 等. NaI (Tl)航测谱仪对137Cs、60Co点源角响应的地面刻度[J].
辐射防护
, 1998, 18(3): 175–184.
LIU Xinhua, ZHANG Yongxing, GU Renkang, et al. Calibration of angel response of a NaI (Tl) airborne spectrometer to 137Cs and 60Co point sources on the ground[J]. Radiation Protection, 1998, 18(3): 175–184. |
| [4] | Sanderson D C W, Mcleod J J, Ferguson J M. A European bibliography on airborne gamma-ray spectrometry[J]. Journal of Environmental Radioactivity, 2001, 53: 411–422. DOI: 10.1016/s0265-931X(00)00145-4 |
| [5] | Grasty R L, Kosanket K L, Foote R S. Fields of view of airborne gamma-ray detectors[J]. Geophysics, 1979, 44(8): 1447–1457. DOI: 10.1190/1.1441017 |
| [6] |
卢存恒, 刘庆成, 韩长青.
空间γ场的弹性变化及应用[M]. 北京: 原子能出版社, 2006: 1-25.
LU Cunheng, LIU Qingcheng, HAN Zhangqing. Elasticity change of spatial gamma field and application[M]. Beijing: Atomic Energy Press, 2006: 1-25. |
| [7] |
倪卫冲, 顾仁康. 核应急航空监测方法[J].
铀矿地质
, 2003, 19(6): 366–373.
NI Weichong, GU Renkang. Airborne monitor method of nuclear emergency response[J]. Uranium Geology, 2003, 19(6): 366–373. |
| [8] |
胡明考, 张积运, 王新兴, 等.大型人工核素平面源校准装置的研建及应用[R].中国科学技术进展报告(第一卷), 2009
HU Mingkao, ZHANG Jiyun, WANG Xinxing, et al.Establishment and application of a large calibration device of artificial radionuclide plane source[R].Progress Report on China Nuclear Science & Technology (Vol.1), 2009 |
| [9] |
韩善彪, 李锦, 陆巍巍, 等. 航空γ谱仪系统校准的基本内容和有关问题探讨[J].
核安全
, 2013, 12(3): 48–52.
HAN Shanbiao, LI Jin, LU Weiwei, et al. Basic contents of calibration of airborne γ spectrometry system and discussion on some related issues[J]. Nuclear Safety, 2013, 12(3): 48–52. |
| [10] |
钱楠, 王德忠, 白云飞, 等. HPGe探测器死层厚度及点源效率函数研究[J].
核技术
, 2010, 33(1): 25–30.
QIAN Nan, WANG Dezhong, BAI Yunfei, et al. Dead layer thickness and efficiency function of point source for HPGe detector[J]. Nuclear Techniques, 2010, 33(1): 25–30. |
| [11] |
周程, 王凤英, 朱晓翔. 无源效率刻度方法的实验验证和分析[J].
核技术
, 2011, 34(8): 604–608.
ZHOU Cheng, WANG Fengying, ZHU Xiaoxiang. Sourceless efficiency calibration method and analysis of experiments[J]. Nuclear Techniques, 2011, 34(8): 604–608. |
| [12] | Gerward L, Guilbert N, Jensen K B, et al. WinXCom-a program for calculating X-ray attenuation coefficients[J]. Radiation Physics and Chemistry, 2004, 71(1): 653–654. DOI: 10.1016/j.radphyschem.2004.04.040 |
| [13] | Wu H X, Zhang H Q, Liu Q C, et al. Information retrieval methods for high resolution γ-ray spectra[J]. Nuclear Science and Techniques, 2012, 23(6): 332–336. |
| [14] | Allyson J D.Environmental gamma-ray spectrometry:simulation of absolute calibration of in-situ and airborne spectrometers for natural and anthropogenic sources[D].Scotland:University of Glasgow, 1994 |
| [15] |
方晟, 曾志, 吴其反, 等. 航空γ谱探测地层中放射性同位素的Monte Carlo模拟计算[J].
清华大学学报(自然科学版)
, 2007, 47(S1): 1018–1021.
FANG Sheng, ZENG Zhi, WU Qifan, et al. Monte Carlo simulations of airborne gamma spectrometry of radionuclide in earth[J]. Journal of Tsinghua University (Science and Technology), 2007, 47(S1): 1018–1021. |
| [16] |
EJ/T 1032-2005:航空伽玛能谱测量规范[S].中华人民共和国核行业标准, 2005:1-25
EJ/T 1032-2005:Specification for airborne gamma-ray spectrometry[S].The People's Republic of China Nuclear Trade Standards, 2005:1-25 |


