压水堆一回路中,放射性核素的主要来源有:水及水中杂质核素受到中子辐照的活化、元件包壳及结构材料的腐蚀产物受到中子辐照的活化、元件棒中裂变产物的泄漏[1]。
水冷聚变堆中,由于不存在裂变产物,因此冷却回路结构材料的活化腐蚀产物和冷却剂的活化产物成为正常运行工况下的最主要放射性来源,也是反应堆运行及维护过程中工作人员辐照剂量的直接来源。反应堆冷却回路结构材料的腐蚀产物(Corrosion Product,CP)释放并在冷却回路内发生沉积,冷却剂中及管壁上的腐蚀产物吸收中子后被活化成为具有放射性的活化腐蚀产物(Activated corrosion products,ACPs)。这些ACPs在管壁或冷却剂中衰变并放出γ射线,其中Fe-55、Mn-56、Cr-51、Mn-54、Co-57、Co-58等是对辐射场贡献较大的几种核素,尤其是Fe-55、Cr-51、Mn-54等长寿命核素,在停堆一段时间后依然会对设备检修工作人员造成辐照伤害,而且一旦发生失水事故(Lost of coolant accident,LOCA),ACPs随冷却剂泄漏到冷却回路以外会污染工作区域并构成安全威胁。在反应堆运行期间,受高能中子的照射,反应堆冷却剂水中的16O和17O吸收中子主要发生以下活化反应:16O(n,p)16N、17O(n,p)17N等。16N和17N衰变时可以放出γ射线,成为反应堆内冷却剂系统放射性的重要来源。在反应堆运行期间接近一回路设备及部件的工作人员会受到活化产物16N和17N的γ辐射影响;在发生瞬态事故,如LOCA事故时,16N和17N也会随冷却剂在破口位置泄漏。这些放射性源项是水冷聚变反应堆冷却回路辐射场的重要来源。
国际上对于活化产物的研究最早见于压水堆[2],经过近50年的不断发展,开发出了十几个机理模型和计算程序,并且大都经过实验数据或电厂运行数据的验证。然而,目前对水冷聚变堆活化腐蚀产物的研究尚处于初步阶段,仅有法国原子能委员会(The French Alternative Energies and Atomic Energy Commission,CEA)开发的PACTITER[3]程序和英国原子能管理局(UK Atomic Energy Authority,UKAEA)开发的TRACT[4]程序,这些程序仅具备结构材料的活化腐蚀计算功能,并且授权使用范围受到了严格限制[2]。然而国际上尚无公开发行的可用版本可以同时计算结构材料的活化腐蚀产物和冷却剂的活化产物。为满足国际热核聚变实验堆(International Thermonuclear Experimental Reactor,ITER)、中国聚变实验试验堆(China Fusion Experiment Test Reactor,CFETR)等聚变设施对水冷回路活化产物源项分析的需求,华北电力大学在CATE V1.0[5]程序的基础上进行升级开发,将均匀模型修改为三节点模型,冷却剂、辐照区和非辐照区作为三个节点,可以更真实地模拟冷却回路结构材料活化腐蚀的行为机理,计算冷却回路管壁内表面腐蚀产物及活化产物的量,并与国际上已有的程序进行了比对验证,结果与其他程序基本吻合,具有一定的可信度[5-6]。另外增加冷却剂活化计算模块,计算16N 和17N的放射性活度,从而使聚变堆放射性源项计算分析更全面更准确。
1 计算模型CATE V2.1程序具备了结构材料的腐蚀活化和冷却剂活化的计算功能,下面将分别详述结构材料活化腐蚀计算模块和冷却剂活化计算模块的计算模型。
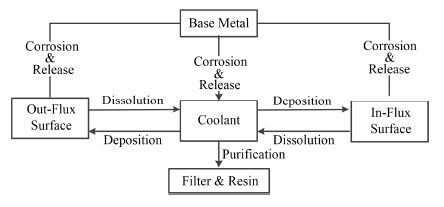
1.1 结构材料活化腐蚀产物计算模型图 1给出了节点划分及物质迁移过程,对结构材料活化腐蚀产物的产生及迁移过程建模,做假设如下:
|
图 1 活化腐蚀产物迁移过程 Figure 1 Transport process of ACPs. |
1) 根据主回路的温度、中子通量密度等将主回路管壁分为两个区域。温度高、受到中子辐照的位置,如第一壁、包层、偏滤器等,称为“辐照区”;温度低、未受到中子辐照的位置,称为“非辐照区”。
2) 冷却剂的流速很快,数十秒即可以在冷却剂回路中循环一周,冷却剂中的活化腐蚀产物核素的半衰期远大于冷却剂在回路中的循环时间,可以认为冷却剂在回路中会迅速被打混,所以假设冷却剂沿回路是处处相同的,所以把冷却剂设定为第三个区域。因此该模型也可称为三节点模型。
3) 假设计算管壁附近的饱和溶解度时采用的是管壁的温度。
4) 在活化腐蚀产物的计算过程中,由于放射性核素的数量和活化截面都远小于稳定核素,因而由活化腐蚀产物核素再活化生成放射性核素的数量远小于由腐蚀产物核素直接活化生成的量,所以放射性核素的产生项中忽略由其他活化腐蚀产物吸收中子发生再活化反应生成的部分。
腐蚀产物的质量平衡方程如下:
辐照区:
| $\frac{\text{d}{{I}_{1}}}{\text{d}t}={}^{{{r}_{\text{C1}}}\centerdot {{S}_{1}}}\!\!\diagup\!\!{}_{\alpha }\;+{{K}_{1}}\left( S\left( {{T}_{1}}+\Delta {{T}_{1}} \right)-S\left( {{T}_{1}} \right) \right)$ | (1) |
非辐照区:
| $\frac{\text{d}{{I}_{3}}}{\text{d}t}={}^{{{r}_{\text{C3}}}\centerdot {{S}_{3}}}\!\!\diagup\!\!{}_{\alpha }\;+{{K}_{3}}\left( S\left( {{T}_{3}}+\Delta {{T}_{3}} \right)-S\left( {{T}_{3}} \right) \right)$ | (2) |
冷却剂:
| $\begin{align} & \frac{\text{d}{{I}_{c}}}{\text{d}t}={{r}_{\operatorname{C}1}}\centerdot {{S}_{1}}+{{r}_{\operatorname{C}3}}\centerdot {{S}_{3}}-{{K}_{1}}\left( S\left( {{T}_{1}}+\Delta {{T}_{1}} \right)-S\left( {{T}_{1}} \right) \right)- \\ & {{K}_{3}}\left( S\left( {{T}_{3}}+\Delta {{T}_{3}} \right)-S\left( {{T}_{3}} \right) \right)-\frac{Q\omega }{{{V}_{F}}}{{I}_{c}}-\sigma \phi {{I}_{c}}\centerdot R \end{align}$ | (3) |
活化产物的浓度平衡方程如下:
辐照区:
| $\begin{align} & \frac{\text{d}{{N}_{1}}}{\text{d}t}=\mathop{\sum }^{}\lambda x{{N}_{n-1}}+\mathop{\sum }^{}\sigma \phi \frac{{{I}_{1}}\centerdot {{N}_{A}}}{A}+ \\ & K_{1}^{a}\left( \frac{{{N}_{c}}}{{{I}_{c}}}S\left( {{T}_{1}}+\Delta {{T}_{1}} \right)-\frac{{{N}_{1}}}{{{I}_{1}}}S\left( {{T}_{1}} \right) \right)- \\ & \lambda {{N}_{1}}-{\sigma }'\phi {{N}_{1}} \end{align}$ | (4) |
非辐照区:
| $\begin{align} & \frac{\text{d}{{N}_{3}}}{\text{d}t}=\mathop{\sum }^{}\lambda x{{N}_{n-1}}+ \\ & K_{3}^{a}\left( \frac{{{N}_{c}}}{{{I}_{c}}}S\left( {{T}_{3}}+\Delta {{T}_{3}} \right)-\frac{{{N}_{3}}}{{{I}_{3}}}S\left( {{T}_{3}} \right) \right)-\lambda {{N}_{3}} \end{align}$ | (5) |
冷却剂:
| $\begin{align} & \frac{\text{d}{{N}_{c}}}{\text{d}t}=\mathop{\sum }^{}\lambda x{{N}_{n-1}}+\mathop{\sum }^{}\sigma \phi \frac{{{I}_{1,k}}\centerdot {{N}_{A}}}{A}- \\ & \mathop{\sum }^{}K_{1}^{a}\left( \frac{{{N}_{c}}}{{{I}_{c}}}S\left( {{T}_{1}}+\Delta {{T}_{1}} \right)-\frac{{{N}_{1}}}{{{I}_{1}}}S\left( {{T}_{1}} \right) \right)- \\ & \mathop{\sum }^{}K_{3}^{a}\left( \frac{{{N}_{c}}}{{{I}_{c}}}S\left( {{T}_{3}}+\Delta {{T}_{3}} \right)-\frac{{{N}_{3}}}{{{I}_{3}}}S\left( {{T}_{3}} \right) \right)- \\ & \lambda {{N}_{c}}-\frac{Q\omega }{{{V}_{F}}}\frac{{{N}_{c}}}{{{I}_{c}}}S\left( {{T}_{c}} \right)-{\sigma }'\phi {{N}_{c}}\centerdot R \end{align}$ | (6) |
式中:rC是腐蚀率,g∙m-2·s-1;S是节点的内表面积,m2;α是腐蚀释放比例;K是传质系数,m3·s-1;S(T)是饱和溶解度,g·m-3;σ是活化截面,barn;f是中子通量密度,n∙m-2·s-1;Q是过滤器旁路流量,m3·s-1,ω是过滤系数;VF是过滤器体积,m3;R是冷却剂在辐照区停留时间与总时间的比值;λ是衰变常数,s-1;x是衰变分支比。
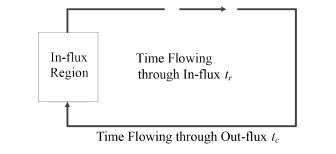
1.2 水活化计算模型假定冷却剂只有在流经辐照区时会受到中子辐照,发生活化反应,因此与结构材料活化腐蚀模型一样将冷却剂回路分为辐照区和非辐照区,但由于冷却剂活化产物中的16N、17N的半衰期只有数秒,在冷却剂循环一周的过程中已经历过多次衰变,因此不能像活化腐蚀产物的计算模型将冷却剂打混。
|
图 2 冷却剂循环示意图 Figure 2 Sketch of coolant circulation. |
冷却剂通过辐照区产生的活化产物的浓度平衡方程如下:
| $\frac{\text{d}N\left( t \right)}{\text{d}t}={{\sigma }_{c}}\phi {{N}_{0}}-\left( \lambda +{{{{\sigma }'}}_{\alpha }}\phi \right)N\left( t \right)$ | (7) |
在辐照区考虑中子活化和再吸收,在非辐照区考虑衰变和净化作用。
运行t=n(tr+tw)时间后冷却剂中的放射性核素的浓度可以用式(8)表示。
t时刻,辐照区及其出口处的浓度:
| $\begin{align} & N\left( t \right)=\text{ }\!\!~\!\!\text{ }\frac{{{\sigma }_{c}}\phi }{{{\alpha }_{w}}-{{\beta }_{w}}}{{N}_{0}}\left( {{\text{e}}^{-{{\beta }_{w}}{{t}_{r}}}}-{{\text{e}}^{-{{\alpha }_{w}}{{t}_{r}}}} \right) \\ & \frac{{{\text{e}}^{-{{\beta }_{w}}{{t}_{r}}}}-{{\text{e}}^{-\alpha {{'}_{w}}{{t}_{r}}}}}{{{\text{e}}^{-{{\beta }_{w}}\left( {{t}_{r}}+{{t}_{c}} \right)}}-{{\text{e}}^{-\alpha {{'}_{w}}\left( {{t}_{r}}+{{t}_{c}} \right)}}} \end{align}$ | (8) |
其中:
| ${{\alpha }_{w}}=\lambda +{{{\sigma }'}_{\alpha }}\phi $ |
| ${{\beta }_{w}}=\frac{\varepsilon Q}{V}+{{\sigma }_{\alpha }}\phi \frac{{{t}_{r}}}{T}$ |
| ${{{\alpha }'}_{w}}=\lambda +\frac{{\varepsilon }'Q}{V}+{{{\sigma }'}_{\alpha }}\phi \frac{{{t}_{r}}}{{{t}_{r}}+{{t}_{c}}}$ |
非辐照区任意位置的活化核浓度:
| ${{N}_{c}}\left( t,x \right)=N\left( t \right)\centerdot {{\text{e}}^{-\left( \lambda +\frac{{\varepsilon }'Q}{V} \right)\centerdot \frac{x}{v}}}$ | (9) |
式中:N(t)是辐照区及出口处活化核的浓度,m3;Nc(t,x)是距离辐照区出口处x处活化核素的浓度,m3;N0是靶核的初始浓度,m3;σc是靶核的活化截面,m2;σ'α是活化核的中子吸收截面,m2;σα是靶核的中子吸收截面;ε是净化装置去除靶核的效率;v是冷却剂平均流速,m·s-1;V是一回路总冷却剂体积,m3。
2 算例及结果 2.1 ITER LIM-OBB回路描述本文将基于聚变堆ITER的包层回路[4]对两种源项进行分析。表 1是包层回路的运行参数。
ITER包层回路使用的材料是SS316[4],文献[4]给出了元素及含量。SS316材料在140-180 ℃的腐蚀率为:
| ${{r}_{\operatorname{C}}}=2.0\times {{10}^{-5}}\times {{t}^{-0.614}}$ | (10) |
在能量为14.1 MeV的中子辐照下,ITER包层冷却回路中的腐蚀产物所涉及到的截面数据以及衰变数据,如衰变分支比、衰变常数等来自于European Activation File EAF-2007[7-8],截面数据以一定能群数的形式储存,在本文的计算中使用的是适用于聚变堆的175群VITAMIN-J结构的截面数据。
| 表 1 包层回路的运行参数 Table 1 The operation parameters of blanket loop. |
使用CATE程序模拟包层回路运行1.2 a,分别给出结构材料活化腐蚀产物和冷却剂活化产物的放射性活度。
2.2.1 结构材料活化腐蚀产物计算结果表 2给出了活化腐蚀产物总和的计算结果,并与当前国际上已有的同类程序PACTITER[3]/ TRACT[4]进行比对。由对比结果可以看出,CATE程序的计算结果与同类程序的结果相比,处在同一个数量级并结果相对保守,在源项领域可以认为CATE程序具有一定的可靠性。CATE程序的计算结果中,对于腐蚀产物,由于冷却剂饱和溶解度的限制,不能承载过多的腐蚀产物,冷却剂中腐蚀产物的量远小于管壁表面氧化层和沉积层腐蚀产物的量,这与腐蚀产物在冷却回路中迁移的方向是一致的。对于活化产物,非辐照区由于不存在中子,活化产物是由辐照区的ACPs释放进入冷却剂,由冷却剂携带在冷却回路迁移到非辐照区并通过同位素交换进入管壁表面,所以辐照区的活化产物会远大于非辐照区。
| 表 2 活化腐蚀产物计算结果 Table 2 The results of ACPs. |
表 3给出了主要放射性核素的比活度。对管壁内表面和冷却剂的放射性活度贡献较大的核素有:56Mn、51Cr、55Fe、58Co、60Co、58mCo、60mCo等,占活化腐蚀产物总量的80%左右。
| 表 3 冷却剂和管壁上的主要放射性核素的比活度 Table 3 The major composition and special activity of ACPs both in coolant and on pipe surface. |
表 4给出了冷却剂受辐照后产生的活化产物16N和17N的总活度。从CATE程序的计算结果来看,在反应堆运行1.2 a后会产生大量的16N和17N,而且放射性活度很大,然而由于16N和17N的半衰期极短,大约10个半衰期后,即100 s之内,其放射性活度降低99.9%以上,1000 s之后可以认为完全衰变完了。
| 表 4 冷却剂活化产物比活度 Table 4 The specific activity of coolant activation products. |
反应堆正常运行期间,与结构材料的活化腐蚀产物相比,16N和17N的放射性活度更大,是总的放射性活度的主要贡献者。而停堆后,16N和17N快速衰变,可以在1000 s之内衰变完,而结构材料的活化腐蚀产物半衰期在数百秒到数年不等,其中的长寿命核素衰变得很慢,这时结构材料的活化腐蚀产物成为冷却剂中放射性活度的主要贡献者。
2.3 剂量率为比较两种活化产物的辐照危害,下面将对两种活化产物的剂量率进行计算。这里使用的计算工具是点核积分程序ARShield,由CATE程序计算的非辐照区的比活度导入ARShield,由ARShield程序将比活度转换为剂量率,计算公式如下:
| $D\left( r \right)=\mathop{\int }^{}\frac{Ks\left( {{r}'} \right)B\left( \mu \left| r\to {r}' \right|,E \right)\text{exp}\left( -\mu \left| r\to {r}' \right| \right)\text{d}V}{2\text{ }\!\!\pi\!\!\text{ }{{\left| r\to {r}' \right|}^{2}}}$ | (11) |
式中:D是由ARShield程序计算得到的剂量率;s是源项,是由CATE程序计算得到的比活度转换而来的。
由于结构材料的活化腐蚀产物核素种类多达一百余种,这里不再给出每种活化腐蚀产物的剂量率。表 5中给出了运行1.2 a、停堆放置15 d后的结构材料活化腐蚀产物和冷却剂活化产物的剂量率。
| 表 5 两种活化产物的剂量率 Table 5 The dose rate of the two kinds of activation products |
由表 5可知,反应堆运行期间,冷却剂活化产物16N产生的剂量率远大于ACPs,而反应堆停堆后,冷却剂活化产物迅速衰变完,不会对剂量率再有贡献,结构材料的活化腐蚀产物核素种类多,半衰期长短不等,停堆15 d后,相比于冷却剂活化产物16N和17N,结构材料活化腐蚀产物中仍有寿命相对较长的放射性核素存在,他们成为了剂量率的主要贡献者。根据ITER设计标准要求,停堆后可进入区域的剂量率要小于100 µSv∙h-1[9],从表 5中数据可知,停堆15 d后的剂量率达到了99.8 µSv∙h-1,15 d后剂量率可满足设计标准的规定。根据国际辐射防护委员会规定的每个工作人员每年接受的剂量不超过20 mSv的要求[10],只考虑活化产物产生的辐射场时,由停堆15 d的接触剂量率可知,保守估计工作人员每年至少可以工作200 h。
3 结语本文对原有的水冷聚变堆源项分析程序CATE进行了升级,并应用新版的CATE程序分别计算了ITER 包层回路中由结构材料的活化腐蚀和冷却剂的活化所产生的放射性产物。接着,使用点核积分程序ARShield将“非辐照区”的结构材料活化腐蚀产物和冷却剂活化产物的比活度转换为剂量。结果表明,反应堆运行期间冷却剂活化产物的比活度和剂量率远大于结构材料活化腐蚀产物,而停堆后冷却剂活化产物迅速衰变完,结构材料的活化腐蚀产物成为比活度和剂量率的主要来源。
| [1] |
刘原中. 轻水堆一迥路中放射性核素浓度的计算方法及计算机程序[J].
辐射防护, 1986, 6 : 409 –424.
LIU Yuanzhong. A method and computer code for calculating radionuclide concentration in primary coolant circuit of LWRs[J]. Radiation Protection, 1986, 6 : 409 –424. (  0) 0)
|
| [2] |
Rafique M, Mirza N M, Mirza S M, et al. Review of computer codes for modeling corrosion product transport and activity build-up in light water reactors[J].
Nukleonika, 2010, 55 (3) : 263 –269.
( 0) 0)
|
| [3] |
Di Pace L, Dacquait F, Schindler P, et al. Development of the PACTITER code and its application to safety analyses of ITER primary cooling water system[J].
Fusion Engineering and Design, 2007, 82 (3) : 237 –247.
DOI: 10.1016/j.fusengdes.2006.11.002 ( 0) 0)
|
| [4] |
Karditsas P J. Activation product transport using TRACT:ORE estimation of an ITER cooling loop[J].
Fusion Engineering and Design, 1999, 45 (2) : 169 –185.
DOI: 10.1016/S0920-3796(99)00004-6 ( 0) 0)
|
| [5] |
Li L, Zhang J Y, Song W, et al. CATE:a code for activated corrosion products evaluation of water-cooled fusion reactor[J].
Fusion Engineering and Design, 2015, 100 : 340 –344.
DOI: 10.1016/j.fusengdes.2015.06.193 ( 0) 0)
|
| [6] |
Zhang J Y, Li L, He S X, et al. Development of a three-zone transport model for activated corrosion products analysis of tokamak cooling water system[J].
Fusion Engineering and Design, 2016, 109-111 : 407 –410.
DOI: 10.7538/yzk.2015.49.S0.0068 ( 0) 0)
|
| [7] |
Forrest R A.
The european activation file:EAF-2007 decay data library[M]. UK: Euratom/Ukaea Fusion Association, 2007 : 8 -40.
( 0) 0)
|
| [8] |
Forrest R A, Kopecky J, Sublet J C.
The european activation file:EAF-2007 neutron-induced cross section library[M]. UK: Euratom/Ukaea Fusion Association, 2007 : 19 -21.
( 0) 0)
|
| [9] |
ITER EDA.
Documentation series No.24:ITER technical basis[M]. Vienna: International Atomic Energy Agency, IAEA, 2002 : 445 -446.
( 0) 0)
|
| [10] |
Valentin J.
The 2007 recommendations of the international commission on radiological protection[M]. Oxford, UK: Elsevier, 2007 : 1 -332.
( 0) 0)
|


