中子散射技术在我国正处于起步阶段。现在,国内正在建设的大型中子散射基地包括位于北京的中国原子能科学研究院的中国先进研究堆、位于广东东莞的中国散裂中子源以及位于四川绵阳的中国工程物理研究院的研究反应堆。除此之外,清华大学工程物理系正在建设一个紧凑型中子源。这些中子源的建设和运行将为国内外研究人员提供难得的物理、化学、材料学和生命科学等学科的研究平台。
金属氧化物团簇是一种非常重要的无机材料,一般的金属氧化物团簇分子的空间尺度约为几个纳米,其表面或者内部具有活性基团[1-3]。金属氧化物团簇被广泛地运用于催化反应以及化学合成。近年来,物质在受限条件下的性质吸引了大批研究人员。将材料置于高度受限的环境之后,材料的动力学、相行为及空间分布等性质均可能发生巨大变化[4-8]。金属氧化物团簇的合成具有高度的可控性,因此,其提供了一个非常好的限制体。通过将高分子链植入金属氧化物团簇分子的内部,可以使这些高分子链处于高度受限制的状态。本文利用中子散射手段研究材料的动力学性质,研究的对象是金属氧化物团簇(Metal oxide cluster)及其内部的碳链。
1 中子散射技术和样品中子散射技术是研究凝聚态物质和材料的物理和化学性质的常见手段[9-11]。携带能量Ei和动量pi的热中子或冷中子,可以与样品中的原子发生强相互作用而被散射,下标“i”代表“散射前”(initial)。散射中子的能量和动量分别记为Ef和动量pf,下标“f”代表“散射后”(final)。在中子散射实验中,入射中子的特征Ei和pi,以及散射中子的特征Ef和pf均被记录。因此,可以得到一个关于中子能量转移E=Ef-Ei和动量转移p=pf-pi的谱函数S(p,E)。E和p均和所研究的系统的结构和分子运动直接相关。因此,通过正确的分析中子散射谱,即可以得到凝聚态物质在分子尺度上的结构和运动的信息。
由于历史原因,在散射文献中,通常使用频率转移ω=(Ef-Ei)/ħ和波矢量转移Q=(pf-pi)/ħ来代替E和p。因此,散射谱通常记为S(Q,ω)。对于各项同性的系统,中子散射谱不依赖于Q的方向,因此,谱函数可记为S(Q,ω)。
按照能量(或频率)转移的取值,中子散射可分为三类:弹性散射(E=0)、准弹性散射(|E|<1 meV)和非弹性散射(|E|>1 meV)。本文所采取的方法为准弹性散射。准弹性中子散射实验在美国橡树岭国家实验室(Oak Ridge National Laboratory)的散裂中子源(Spallation Neutron Source)装置上完成。相应的谱仪为背散射谱仪(BL-2 BASIS)[12]。该谱仪的能量分辨率约为3.4 µeV,能量转移范围为-120-120 µeV。这样的能量参数对应的时间尺度为几十个皮秒到几十个纳秒。波矢转移范围为3-17 nm-1,对应的空间尺度为0.37-2.1 nm。因此,该谱仪十分适合研究分子尺度上的凝聚态物质的动力学。
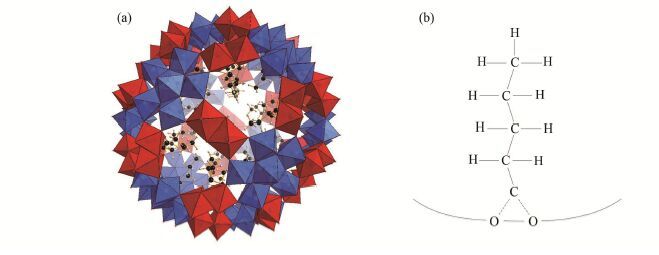
研究的样品是金属氧化物团簇与其内部包裹的碳链。金属氧化物团簇分子呈中空的球形,其分子式为[MoVI72MoV60O372(C4H9COO)24(H2O)84]36-。分子的外直径为3 nm,内直径为2 nm。在内部有30个碳链,每个碳链均含有5个碳原子。图 1(a)给出了一个金属氧化物团簇分子和其内部的碳链的结构示意图,其中多边形表示MoVIO6、MoVIO7或者MoVO6,大圆球表示碳原子,小圆球表示氢原子,虚线表示配位键,实线表示共价键。图 1(b)给出了一个碳链的结构。可以看到,该碳链的一端通过配位键与球壳上的氧原子相连接,另一端则是自由的甲基。
|
图 1 金属氧化物团簇示意图(a)和金属氧化物团簇内部的一个碳链的结构示意图(b) Figure 1 Polyhedron representation of the molecular structure of the metal oxide cluster (a) and the structure of one polymer chain confined in the metal oxide cluster molecule (b). |
凝聚态物质的中子谱包括两个部分:相干散射(Coherent scattering)和非相干散射(Incoherent scattering)[9]:
| $S(Q,\omega )={{S}_{coh}}(Q,\omega )+{{S}_{inc}}(Q,\omega )$ | (1) |
相干散射部分反映凝聚态物质内原子或者分子的集体性质,例如结构、集体运动。而非相干散射部分反映的则是原子或者分子的个体行为。要特别强调,氢原子的非相干散射截面远大于其他元素的散射截面(一般为2-4个数量级)[9-11],因此,如果样品中含有大量氢原子,测得的中子谱的信号将主要由氢原子的非相干散射造成。本文研究的样品中的碳链上含有大量氢原子,因此,所得到的中子谱可近似看成是碳链上的氢原子的非相干散射谱。
样品的准弹性中子谱记为SH(Q,ω),下标“H”表示中子谱主要反映系统中氢原子的运动。它具有如下傅里叶变换的形式[9]:
| ${{S}_{H}}(Q,\omega )=\frac{1}{2\pi }\int_{-\infty }^{\infty }{{{F}_{H}}(Q,t){{e}^{-i\omega t}}dt}$ | (2) |
式中:FH(Q,t)通常被称为中间散射函数(Intermediate scattering function)[9]:
| ${{F}_{H}}(Q,t)={\left\langle \sum\limits_{l=1}^{{{N}_{H}}}{{{e}^{iQ\times [{{r}_{l}}(t)-{{r}_{l}}(0)]}}} \right\rangle }/{{{N}_{H}}}\;$ | (3) |
式中:NH是系统中氢原子的总数;rl(t)是第l个氢原子在t时刻的位置向量;代表系综平均。一般而言,氢原子的运动可分解为三部分:振动(vibration)、平动(translation)和转动(rotation)。这里分别用FV(Q,t)、FT(Q,t)和FR(Q,t)来表示。对于常温下的分子,这三个运动之间没有明显的耦合,因此,氢原子的总运动可表示为上述三个分运动的独立叠加[6, 11]:
| ${{F}_{\text{H}}}(Q,t)\approx {{F}_{\text{V}}}(Q,t){{F}_{\text{T}}}(Q,t){{F}_{\text{R}}}(Q,t)$ | (4) |
振动部分是由于热运动造成的,这一部分在物理原理上较为简单清晰,往往利用德拜-沃勒尔因子(Debye-Waller factor)表示[9, 11]:
| ${{F}_{V}}(Q,t)={{e}^{-{{Q}^{2}}\left\langle {{u}^{2}} \right\rangle /3}}$ | (5) |
式中:<u2>是氢原子在仪器的时间尺度内的均方位移(Mean square displacement)。注意,德拜-沃勒尔因子并不依赖于时间。
氢原子的平动被金属氧化物团簇的强约束效应所抑制,因此,可近似地看作在受限空间内的扩散运动[13-15]:
| ${{F}_{T}}(Q,t)=A(Q)+[1-A(Q)]{{e}^{-{{\left( \frac{t}{{{\tau }_{T}}(Q)} \right)}^{\beta }}}}$ | (6) |
式中:tT(Q)即氢原子在动量转移为Q的时候平动的弛豫时间;β为拉伸因子。在一般的扩散过程中,分子的运动关联函数是指数衰减的形式,即β=1。这里,由于系统内部运动的受限性以及不均匀性,引入不等于1的拉伸因子是非常必要的。
另外要注意的是,式(6)中存在一个不依赖时间的项A(Q),它的存在是由于平动在空间中的受限性造成的,它的值介于1和0之间。当平动的范围是无限空间时,其值为0;而当平动完全被限制,即固定不动时,其值为1。可见,A(Q)是重要的反映系统运动在空间中受约束程度的量[6]。
转动部分可以用转动扩散模型来表示[16]:
| ${{F}_{R}}(Q,t)=\sum\limits_{l=1}^{\infty }{(2l+1){{j}_{l}}{{(Qb)}^{2}}{{e}^{-l(l+1){{D}_{r}}t}}}$ | (7) |
式中:jl(x)是第l阶球贝塞尔函数;b是转动半径,即为甲基或亚甲基中碳氢键的长度;Dr是转动扩散系数,它的大小直接反映了转动的快慢。注意到,式(7)是一个无限级数的形式,而实际在实验的Q范围内,前四项已经足够表示系统中氢原子的转动了。
在具体分析数据时,需要将实验数据和理论模型做非线性拟合:
| ${{S}_{\text{H},\exp }}(Q,\omega )={{S}_{\text{H},\text{theo}}}(Q,\omega )*R(Q,\omega )$ | (8) |
式中:SH,exp(Q,ω)代表实验测得的中子谱;SH,theo(Q,ω)为理论模型得到的谱;R(Q,ω)为仪器的能量分辨率函数;*代表卷积运算。通过这样的非线性拟合程序,可以将4个拟合系数:A(Q)、tT(Q)、β和Dr求出,从而得到金属氧化物内部碳链的运动情况。
总之,这里的理论模型采取了最常见的运动模型。平动部分主要反映碳链上的碳原子的运动,而转动部分则反映氢原子围绕其相应的碳原子的转动。该模型在受限制条件下的水以及其他分子的运动的分析中被广泛运用[6, 8, 11]。利用该模型,Wang等[8]成功地分析得到了类似系统,即多酸约束下高分子的运动情况。下一节中,将具体介绍本次实验结果并与先前他人得到的结果做比较。将会看到,金属氧化物团簇对于内部的碳链的运动有极强的约束效应。
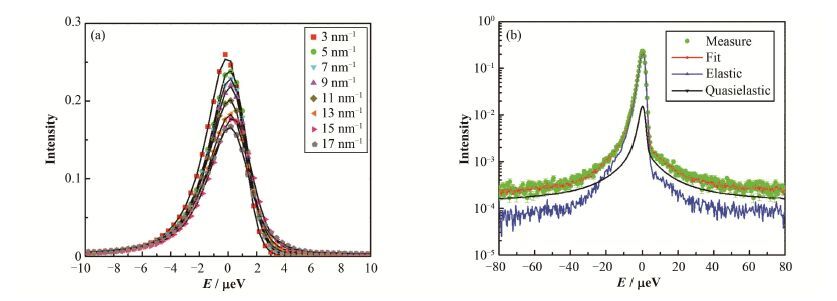
3 实验结果及讨论实验测得的中子谱以及通过式(8)拟合得到的拟合曲线在图 2中给出。图 2(a)给出了所有测得的中子谱在线性坐标下的情况,该图反映了拟合整体质量。图 2(b)给出了Q=5 nm-1时,实验谱与理论拟合曲线在对数坐标下的对比情况,该图反映了拟合的细节。另外,在图 2(b)中,我们给出了弹性散射(Elastic)和准弹性散射(Quasielastic)的贡献。可以看出,弹性散射的贡献占有较大的份额。
|
图 2 所有实验测量得到的中子谱与理论拟合曲线在线性坐标下的对比(a)和在Q=5 nm-1处在对数坐标下的对比(b) Figure 2 Comparison between the experimental spectra and the fitted curves in linear scale (a) and in logarithmic scale at Q=5 nm-1 (b). |
首先讨论系统中氢原子的均方位移<u2>。这里先介绍求取均方位移的方法。由式(5)可知,均方位移对应于氢原子的运动中的振动部分,这一部分并不依赖于时间,因此,在能量域,其对应于弹性散射的部分为:
| ${{I}_{el}}(Q,T)={{e}^{-{{Q}^{2}}\left\langle {{u}^{2}}(T) \right\rangle /3}}$ | (9) |
式中:Iel(Q,T)为在温度为T和能量转移为Q的情况下,中子谱的弹性散射部分。从式(9)容易得到:
| $\left\langle {{u}^{2}}(T) \right\rangle -\left\langle {{u}^{2}}({{T}_{0}}) \right\rangle =-\frac{3}{{{Q}^{2}}}\ln \left( \frac{{{I}_{\text{el}}}(Q,T)}{{{I}_{\text{el}}}(Q,{{T}_{0}})} \right)$ | (10) |
式中:T0为某个接近于0 K的基准温度。当温度趋于0 K时,氢原子的振动也趋于0,此时有(这里忽略量子效应,即假设振动的零点能为0):
| $\left\langle {{u}^{2}}({{T}_{0}}) \right\rangle \approx \left\langle {{u}^{2}}(0) \right\rangle =0$ | (11) |
联立式(10)和(11),得:
| $\ln \left( \frac{{{I}_{\text{el}}}(Q,T)}{{{I}_{\text{el}}}(Q,{{T}_{0}})} \right)=-\frac{1}{3}{{Q}^{2}}\left\langle {{u}^{2}}(T) \right\rangle $ | (12) |
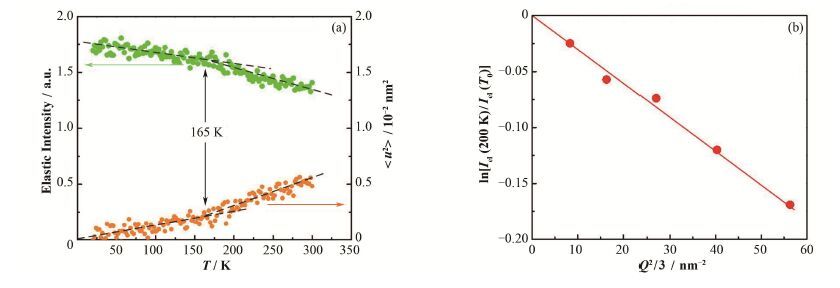
通过对ln[Iel(Q,T)/Iel(Q,T0)]和Q2/3做线性拟合,即可得到该温度下<u2>的值。图 3(a)给出了弹性散射扫描的结果,同时也给出了利用式(9)-(12)计算得到的均方位移的结果。图 3(b)给出了如式(12)所示的一个典型的线性拟合。
|
图 3 弹性散射强度和均方位移随温度的变化(a),利用式(12)做线性拟合求取均方位移的一个例子(温度为200 K)(b) Figure 3 Elastic scattering intensity and the mean square displacement as a function of temperature (a),an example of using Eq.(12) to obtain the mean square displacement (T = 200 K) (b). |
从图 3(a)可看出,在T<165 K时,均方位移随着温度呈线性增加。这意味着在该温度范围内,氢原子的运动即为在平衡位置附近做热振动。而在165 K附近,均方位移关于温度的函数的斜率发生了一定的升高,这是由于有不同于热振动的新的运动自由度被激发所造成的。Roh等[17]曾经研究过蛋白质中的氢原子的均方位移,并发现在100 K附近也有类似的均方位移的加强,他们将这个转变归因于甲基转动被激发。我们研究的系统中,均方位移在165 K的增强也应由于甲基转动被激发造成,而约65 K的温度差则应该是由于碳链被约束得更加严重,从而导致甲基转动更难被激发。
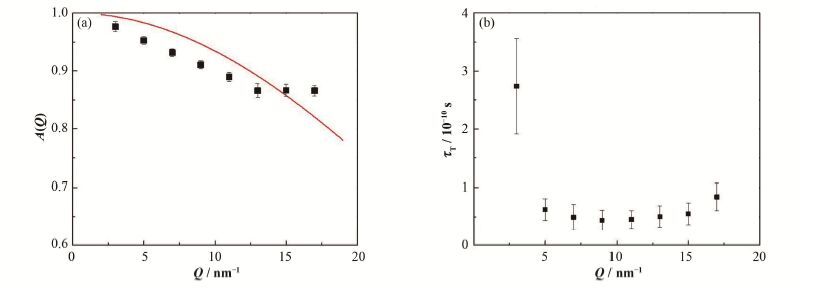
图 4(a)给出了A(Q)的测量结果。如前文所述,A(Q)可以定量地描述碳链的平动的受约束的情况。实际上,若视碳链上的碳原子的平动为一个在半径为a的封闭圆球中的运动,则A(Q)有如下表达式[6]:
| $A(Q)={{\left( \frac{3{{j}_{1}}(Qa)}{Qa} \right)}^{2}}$ | (13) |
|
图 4 实验得到的A(Q)及用式(13)拟合得到的结果(a),氢原子的平动弛豫时间(b) Figure 4 Experimental A(Q) and the fitting result obtained by fitting with Eq.(13) (a),translational relaxation time of the hydrogen atom (b). |
我们将实验得到的A(Q)与式(13)做拟合,拟合结果同样表示于图 4(a)之中。注意当Q>15 nm-1时,实验得到的A(Q)的取值与拟合结果有些许偏离。这应该是由于Q较大的中子谱对应较为局域的运动,这时,运动的细节变得很重要,简单的扩散加上拉伸因子的模型不再能够非常准确地描述碳原子的平动。拟合得到的限制半径a=(0.058 1±0.003 4) nm,注意到这个数值非常小,甚至小于碳原子本身的直径。这表明,在金属氧化物团簇的内部,碳链没有任何做大尺度平动的空间,这与一般的高分子材料中的碳链的形态有根本的区别。在一般的高分子材料或有机材料中,碳链可以做大范围的形态变化(例如高分子单体的排布可具有高斯分布,且其密度的涨落可以较大)。而在本材料中,碳链在平衡态下几乎被固定,这一点也就是本文所强调的金属氧化物团簇的“强约束”效应,该效应对于金属氧化物团簇的包裹(Encapsulation)行为有决定性影响[8]。
图 4(b)给出了平动的弛豫时间tT(Q)。其数量级大约在几十到几百皮秒。这样的数据是合理的,也非常接近于强受限环境中的水分子的平动弛豫时 间[13-15]。另外,拉伸因子β的拟合结果为β=0.782±0.045,它的取值不接近于1说明在每一个碳链上,各个碳原子的平动有较强的不均匀 性[18-19]。这一点也是符合系统实际情况的,每一条碳链上都有5个碳原子,它们的位置不同,所获得的运动的空间和受到的约束也不同,因此,它们的运动情况也必然是不同的。
拟合得到的Dr的值为5.19×107 s-1,这意味着氢原子的转动弛豫时间为tr≈1/2Dr=1.93×10-8 s。这样的结果也是较为让人感到惊异的,在通常的高分子材料或者生物材料中,甲基或亚甲基转动的弛豫时间常在10-10 s量级[17, 20]。这里氢原子的转动比其他材料慢了两个数量级,这说明在本文研究的材料中,甲基和亚甲基均受到了很强的作用,从而导致上面的氢原子转动速度大幅度变慢。而这种很强的相互作用,也来源于金属氧化物团簇对于其内部碳链的强约束效应。
本文所研究的样品的碳链长度为5个碳原子。最近,Wang等[8]研究了相似的系统,他们的样品中,碳链的长度为4个碳原子。本文研究的样品中的碳链长度更长,因此,碳链运动可利用的空间更小,强约束效应更明显,而这也被分析结果所证实。在Wang等[8]的研究中,均方位移发生转变的温度约为150 K,转动的弛豫时间为5×10-9 s。本文中,这两个量分别为165 K和1.93×10-8 s,更高的转变温度以及更慢的转动均体现了更强的约束效应。另外,Wang等[8]得到的碳链的平动受限半径为0.052 nm,与本文中的结论0.058 nm非常接近,这说明对于碳链的平动的约束在碳链长度为4个碳原子时就已经达到饱和。
4 结语本文利用准弹性中子散射技术研究了金属氧化物团簇内部的碳链的运动。在分析数据时,碳链上的氢原子运动分解为三个独立的部分,即振动、平动和转动。结果表明,这些碳链的运动被高度抑制,主要表现在:1) 碳链上氢原子均方位移虽然在165K发生了增强,但增强幅度很小,远达不到自由扩散或者其他大尺度随机运动的标准;2) 碳链上的碳原子的运动在空间上高度受限,且受限空间半径仅为0.058 nm,这表明碳链上的碳原子不具备任何大尺度运动的条件,其运动仅为在平衡位置附近的振动;3) 氢原子的转动远慢于大多数的高分子材料和生物材料中的甲基或亚甲基的转动。本文证明,金属氧化物团簇对于内部的碳链的运动具有强约束效应。
致谢 感谢美国橡树岭国家实验室的殷盼超博士提供样品以及王哲博士在实验数据分析上的帮助| [1] |
Kopilevich S, Gil A, Garcia-Ratés M, et al. Catalysis in a porous molecular capsule:activation by regulated access to sixty metal centers spanning a truncated icosahedron[J].
Journal of American Chemistry Society, 2012, 134 : 13082 –13088.
DOI: 10.1021/ja304513t ( 0) 0)
|
| [2] |
Kopilevich S, Müller A, Weinstock I A. Amplified rate acceleration by simultaneous up-regulation of multiple active sites in an endo-functionalized porous capsule[J].
Journal of American Chemistry Society, 2015, 137 : 12740 –12743.
DOI: 10.1021/jacs.5b06211 ( 0) 0)
|
| [3] |
Yin P, Wu B, Mamontov E, et al. X-ray and neutron scattering study of the formation of core-shell-type polyoxometalates[J].
Journal of American Chemistry Society, 2016, 138 : 2638 –2643.
DOI: 10.1021/jacs.5b11465 ( 0) 0)
|
| [4] |
Zhou H C, Long J R, Yaghi O M. Introduction to metal-organic frameworks[J].
Chemical Review, 2012, 112 : 673 –674.
DOI: 10.1021/cr300014x ( 0) 0)
|
| [5] |
Wang Z, Ito K, Leão J B, et al. Liquid-liquid phase transition and its phase diagram in deeply-cooled heavy water confined in a nanoporous silica matrix[J].
Journal of Physical Chemistry Letters, 2015, 6 : 2009 –2014.
DOI: 10.1021/acs.jpclett.5b00827 ( 0) 0)
|
| [6] |
Bellissent-Funel M C, Chen S H, Zanotti J M. Single-particle dynamics of water molecules in confined space[J].
Physical Review E, 1995, 51 : 4558 .
DOI: 10.1103/PhysRevE.51.4558 ( 0) 0)
|
| [7] |
李华, 张丽丽, 易洲. 准弹性中子散射(QENS)在受限水动态研究中的应用[J].
核技术, 2014, 37 : 020604 .
DOI: 10.11889/j.0253-3219.2014.hjs.37.020604 LI Hua, ZHANG Lili, YI Zhou. Application of quasi-elastic neutron scattering to dynamics study of confined water[J]. Nuclear Techniques, 2014, 37 : 020604 . DOI: 10.11889/j.0253-3219.2014.hjs.37.020604 (  0) 0)
|
| [8] |
Wang Z, Daemen L L, Cheng Y, et al. Nanoconfinement inside molecular metal oxide clusters:dynamics and modified encapsulation behavior[J].
Chemistry, 2016, 22 : 14131 –14136.
DOI: 10.1002/chem.201603239 ( 0) 0)
|
| [9] |
Chen S H, Kotlarchyk M.
Interaction of photons and neutrons with matter:an introduction[M]. Singapore: World Scientific, 1997 .
( 0) 0)
|
| [10] |
Chen S H. Small angle neutron scattering studies of the structure and interaction in micellar and microemulsion systems[J].
Annual Reviews of Physical Chemistry, 1986, 37 : 351 –399.
DOI: 10.1146/annurev.pc.37.100186.002031 ( 0) 0)
|
| [11] |
Bée M.
Quasielastic neutron scattering[M]. Bristol: Adam Hilger, 1988 .
( 0) 0)
|
| [12] |
Mamontov E, Herwig K W. A time-of-flight backscattering spectrometer at the spallation neutron source, BASIS[J].
Review of Scientific Instruments, 2011, 82 : 085109 .
DOI: 10.1063/1.3626214 ( 0) 0)
|
| [13] |
Wang Z, Fratini E, Li M, et al. Hydration-dependent dynamic crossover phenomenon in protein hydration water[J].
Physical Review E, 2014, 90 : 042705 .
DOI: 10.1103/PhysRevE.90.042705 ( 0) 0)
|
| [14] |
Liu L, Chen S H, Faraone A, et al. Pressure dependence of fragile-to-strong transition and a possible second critical point in supercooled confined water[J].
Physical Review Letters, 2005, 95 : 117802 .
DOI: 10.1103/PhysRevLett.95.117802 ( 0) 0)
|
| [15] |
Wang Z, Le P, Ito K, et al. Dynamic crossover in deeply cooled water confined in MCM-41 at 4 kbar and its relation to the liquid-liquid transition hypothesis[J].
Journal of Chemical Physics, 2015, 143 : 114508 .
DOI: 10.1063/1.4930855 ( 0) 0)
|
| [16] |
Sears V F. Cold neutron scattering by molecular liquids III:methane[J].
Canadian Journal of Physics, 1967, 45 : 237 –254.
DOI: 10.1139/p67-025 ( 0) 0)
|
| [17] |
Roh J H, Novikov V N, Gregory R B, et al. Onsets of anharmonicity in protein dynamics[J].
Physical Review Letters, 2005, 95 : 038101 .
DOI: 10.1103/PhysRevLett.95.038101 ( 0) 0)
|
| [18] |
Ediger M D, Angell C A, Nagel S R. Supercooled liquids and glasses[J].
Journal of Physical Chemistry, 1996, 100 : 13200 –13212.
DOI: 10.1021/jp953538d ( 0) 0)
|
| [19] |
Berthier L, Biroli G. Theoretical perspective on the glass transition and amorphous materials[J].
Reviews of Modern Physics, 2011, 83 : 587 –645.
DOI: 10.1103/RevModPhys.83.587 ( 0) 0)
|
| [20] |
Colmenero J, Moreno A J, Alegría A. Neutron scattering investigations on methyl group dynamics in polymers[J].
Progress in Polymer Science, 2005, 30 : 1147 –1184.
DOI: 10.1016/j.progpolymsci.2005.08.001 ( 0) 0)
|
