2. 东华理工大学 放射性地质与勘探技术国防重点实验室 南昌 330013
2. Fundamental Science on Radioactive Geology and Exploration Technology Laboratory, East China Institute of Technology, Nanchang 330013, China
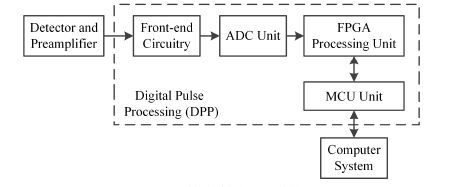
20世纪90年代以来,随着电子技术的发展,传统的模拟核仪器系统逐渐向数字化方向发展。数字核仪器系统结构如图 1所示,探测器输出信号经前端电路滤波成形后,进入模数转换器(Analog-to- digital Converter,ADC)采样,随后被直接被送入现场可编程门阵列(Field-Programmable Gate Array,FPGA)处理单元进行数字处理及幅度甄别,最后通过微控制单元(Microcontroller Unit,MCU)将谱数据传送至计算机进行分析。除在结构上简化了模拟核仪器系统,数字核仪器系统在核信号滤波成形方面采用了数字算法,在实时性、灵活性、稳定性等方面都有了很大改进。由于高速ADC的使用,叠加在信号中的噪声也被采集,为减小噪声对测量结果的影响,需要对ADC采样后的数字信号进行数字滤波成形处理。常用的数字滤波成形方法包括梯形脉冲成形和高斯脉冲成形。梯形脉冲成形兼顾能量分辨率和计数率[1-5],被广泛应用于数字核仪器系统中。高斯脉冲具有良好的时间响应、频率响应和较高的信噪比,在数字核仪器系统中,前端电路通常将探测器输出信号滤波成形为高斯波形或类高斯波形[6]。例如,Hallgren等[7-10]采用Sallen-Key (S-K)滤波器将探测器输出信号成形为高斯波形。另外,利用CR-nRC滤波器可得到类高斯波形[11-13]。除了用电子元器件实现高斯脉冲成形外,部分学者对高斯脉冲成形数字实现方法也进行了研究。陈世国 等[14-15]研究小波分析方法实现了指数衰减信号高斯脉冲成形;Nakhostin[16]通过CR-nRC滤波器,得到类高斯脉冲成形的递推算法。本文从模拟高斯脉冲成形电路出发,在已有的高斯脉冲成形算法基础上,新引入截止频率和品质因子,研究其成形参数的选择及在数字核仪器系统中的应用。
|
图 1 数字核仪器系统 Figure 1 Digital nuclear spectrometer system. |
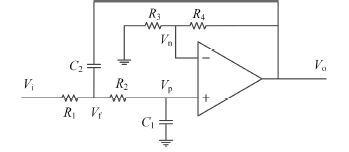
低通Sallen-Key滤波器在核电子学中被广泛应用于核信号的滤波成形,它可以在较少的级数下得到类高斯波形的输出,并且有较大的品质因子。图 2是低通S-K滤波器电路原理图。根据基尔霍夫电流定律可以建立低通S-K滤波器的电流等式,如式(1)所示。
|
图 2 低通S-K滤波器电路原理图 Figure 2 Scheme of low-pass S-K filter. |
| $\left\{ \begin{align} & \frac{{{V}_{\operatorname{i}}}-{{V}_{\operatorname{f}}}}{{{R}_{1}}}=\frac{\operatorname{d}({{V}_{\operatorname{f}}}-{{V}_{\text{o}}})}{\operatorname{d}t}\cdot {{C}_{2}}+\frac{{{V}_{\operatorname{f}}}-{{V}_{\operatorname{p}}}}{{{R}_{2}}} \\ & \frac{{{V}_{\operatorname{f}}}-{{V}_{\operatorname{p}}}}{{{R}_{2}}}=\frac{\operatorname{d}{{V}_{\operatorname{p}}}}{\operatorname{d}t}\cdot {{C}_{1}} \\ & {{V}_{\operatorname{n}}}=(\frac{{{R}_{3}}}{{{R}_{3}}+{{R}_{4}}})\cdot {{V}_{\operatorname{o}}} \\ & {{V}_{\operatorname{p}}}={{V}_{\operatorname{n}}}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \\ \end{align} \right.$ | (1) |
式中:Vi、Vo、Vn、Vp和Vf分别表示对应节点的电压值;R1、R2、R3、R4为对应电阻的阻值;C1、C2为对应电容的容值。整理可得:
| $\begin{align} & {{R}_{1}}{{C}_{1}}{{R}_{2}}{{C}_{2}}\cdot \frac{{{d}^{2}}{{V}_{\operatorname{o}}}}{d{{t}^{2}}}+ \\ & \,({{R}_{1}}{{C}_{2}}+{{R}_{1}}{{C}_{1}}-K\cdot {{R}_{1}}{{C}_{2}}+{{R}_{2}}{{C}_{1}})\cdot \frac{d{{V}_{\operatorname{o}}}}{dt}+{{V}_{\operatorname{o}}}=K\cdot {{V}_{\operatorname{i}}} \\ \end{align}$ | (2) |
式中:K为成形脉冲的幅度放大倍数,其值的选择与输出信号的品质因子有关,K=(1+R4/R3)。本文新引入截止频率fc和品质因子Q,研究成形参数的选择,即:
| ${{f}_{\operatorname{c}}}=\frac{1}{2\pi \sqrt{{{R}_{1}}{{R}_{2}}{{C}_{1}}{{C}_{2}}}}$ | (3) |
| $Q=\frac{\sqrt{{{R}_{1}}{{R}_{2}}{{C}_{1}}{{C}_{2}}}}{{{R}_{1}}{{C}_{1}}+{{R}_{2}}{{C}_{1}}+{{R}_{1}}{{C}_{2}}(1-K)}$ | (4) |
为实现截止频率和品质因子单独控制,对图 2中R1、R2、C1、C2进行简化。令R1=R2=R,C1=C2=C,τ=RC,则式(2)可简化为:
| ${{(RC)}^{2}}\cdot \frac{{{\operatorname{d}}^{2}}{{V}_{\operatorname{o}}}}{\operatorname{d}{{t}^{2}}}+(3-K)RC\cdot \frac{\operatorname{d}{{V}_{\operatorname{o}}}}{\operatorname{d}t}+{{V}_{\operatorname{o}}}=K\cdot {{V}_{\operatorname{i}}}$ | (5) |
在原有低通S-K滤波器数学模型基础上[17],由式(3)、(4)、(5)可得到含有截止频率和品质因子的高斯脉冲成形算法,如式(6) :
| $\left\{ \begin{align} & {{V}_{\operatorname{o}}}[n]=\frac{[2{{\tau }^{2}}+\tau \cdot (3-K)]\cdot {{V}_{\operatorname{o}}}[n-1]}{{{\tau }^{2}}+\tau \cdot (3-K)+1}- \\ & \quad \quad \quad \frac{{{\tau }^{2}}\cdot {{V}_{\operatorname{o}}}[n-2]+K\cdot {{V}_{\operatorname{i}}}[n]}{{{\tau }^{2}}+\tau \cdot (3-K)+1} \\ & {{f}_{\operatorname{c}}}=\frac{1}{2\tau \pi } \\ & Q=\frac{1}{3-K}\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \\ \end{align} \right.$ | (6) |
式中:τ为成形脉冲的成形时间,其值的选择与滤波器的截止频率有关。
2 高斯脉冲成形算法实验测试 2.1 成形参数对输出信号波形的影响为研究τ和K值对输出信号的影响,采用实测核信号进行实验。实测信号由硅漂移半导体探测器(Silicon Drift Detector,SDD)探测,经高通滤波和线性放大后被转换速率为20×106s-1的ADC采样得到。选择不同的τ和K值进行实验,实验结果如图 3所示。
|
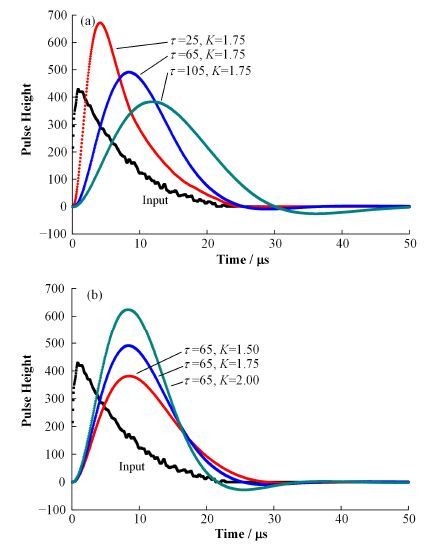
图 3 不同成形时间(a)和不同幅度放大倍数(b)下高斯脉冲成形 Figure 3 Gaussian pulse shaping with different shaping times (a) and different amplification factors (b). |
由图 3(a)可以看出,当K值不变时(K=1.75,Q=0.8),随着τ值增大,成形脉冲下降沿变缓,幅度降低,宽度变宽,极点后移;图 3(b)则说明,当τ值不变时(τ=65,fc=50 kHz),随着K值增大,成形脉冲波形下降沿变快,幅度增大,宽度变窄,极点前移。
结合式(6)可知,K值的选择受输出信号品质因子的约束,实验证明当K接近于3时,输出信号出现振荡。在实际应用中,K值的选取应在2附近,以得到最大品质因子的输出信号。τ值与滤波器的截止频率有关,当τ值较大时虽然对输入信号的滤波能力越强,但增加了脉冲宽度。应用时可通过比较滤波前后输入信号的频谱图确定最优τ值,同时τ值较小时(图 3(a)中τ=25),成形脉冲无下冲。
2.2 噪声抑制为研究高斯脉冲成形算法在滤波方面的性能,采用常用的梯形脉冲成形算法作对比研究。核信号用负指数函数模拟,并叠加高斯白噪声。梯形脉冲成形采用Imperiale提出的算法[3],如式(7)所示。
| $\left\{ \begin{matrix} \begin{align} & {{V}_{\operatorname{o}}}[n]=2{{V}_{\operatorname{o}}}[n-1]-{{V}_{\operatorname{o}}}[n-2]+\{{{V}_{\operatorname{i}}}[n-1]- \\ & {{V}_{\operatorname{i}}}[n-{{n}_{\operatorname{a}}}-1]-{{V}_{\operatorname{i}}}[n-{{n}_{\text{b}}}-1]+ \\ & {{V}_{\operatorname{i}}}[n-{{n}_{\operatorname{c}}}-1]-{{\text{e}}^{-{{T}_{\operatorname{s}}}/{{\tau }_{\operatorname{i}}}}}\cdot [{{V}_{\operatorname{i}}}[n-2]- \\ & {{V}_{\operatorname{i}}}[n-{{n}_{\operatorname{a}}}-2]-{{V}_{\operatorname{i}}}[n-{{n}_{\operatorname{b}}}-2]+ \\ & {{V}_{\operatorname{i}}}[n-{{n}_{\operatorname{c}}}-2]]\}\cdot \frac{1}{{{n}_{\operatorname{a}}}} \\ \end{align} & (n\ge 1) \\ {{V}_{\operatorname{o}}}[n]={{V}_{\operatorname{i}}}[n]=0 & (n <1) \\ \end{matrix} \right.$ | (7) |
式中:Vi、Vo分别表示输入、输出信号;na、nc分别表示梯形脉冲的上升时间和脉冲宽度;nb表示梯形脉冲上升时间与平顶宽度之和,即nc=na+nb;Ts表示ADC的采样率;τi为输入核信号的衰减时间常数。两种滤波成形算法得到的成形脉冲具有相同达峰时间。
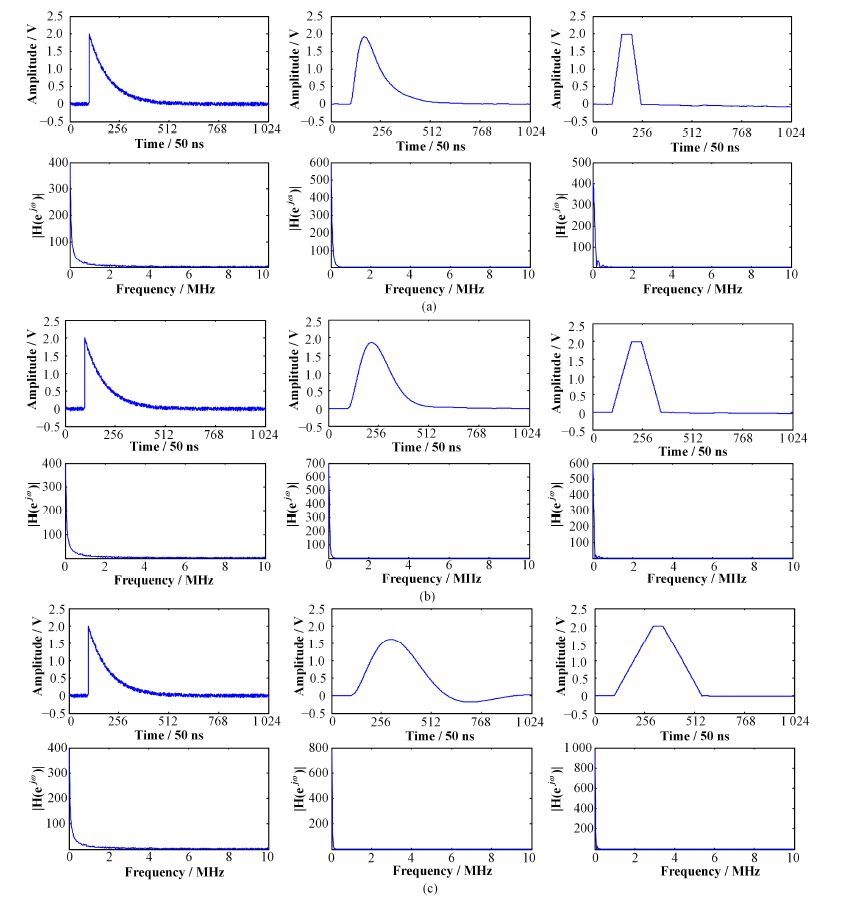
模拟核信号的幅度为2V,衰减时间常数为5μs,分别进行高斯脉冲成形和梯形脉冲成形处理,结果如图 4所示。第一组为核信号和对应的高斯成形、梯形成形脉冲结果;第二组为对应信号的频 谱图。
|
图 4 高斯脉冲成形与梯形脉冲成形 a) τ=25,K=1.5,na=50,nb=100,(b) τ=50,K=1.75,na=100,nb=150,(c) τ=100,K=2,na=200,nb=250 Figure 4 Gaussian pulse shaping and trapezoidal pulse shaping (a) τ=25,K=1.5,na=50,nb=100,(b) τ=50,K=1.75,na=100,nb=150,(c) τ=100,K=2,na=200,nb=250 |
由图 4中成形脉冲的频谱图可以看出,随着τ、na值的增大,两种方法的滤波效果均变好;对比两种方法得到成形脉冲的频谱图可得,在相同达峰时间条件下,高斯脉冲成形算法较梯形脉冲成形算法有更好的噪声抑制能力。
利用MATLAB生成2×105个带高斯白噪声的负指数信号模拟原始核信号,分别做两组实验:
1) 对原始核信号先进行高斯脉冲成形,再做幅度甄别,成形参数τ=15,K=2(Q=1,使得输出信号品质最佳);
2) 对原始核信号先进行相同达峰时间的梯形脉冲成形,再做幅度甄别,成形参数为na=30,nb=50。
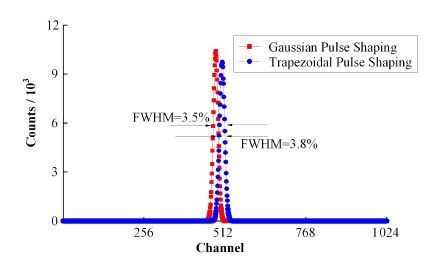
实验所得幅度谱如图 5所示。从图 5中可以看出,在不考虑堆积脉冲的情况下,采用高斯脉冲成形算法所得幅度谱的半高宽(Full Width at Half Maximum,FWHM)较采用梯形脉冲成形算法所得幅度谱的半高宽值提高了7.9%,高斯脉冲成形算法适用于核信号滤波处理。
|
图 5 高斯脉冲成形与梯形脉冲成形半高宽对比 Figure 5 Comparison of Gaussian pulse shaping and trapezoidal pulse shaping on FWHM. |
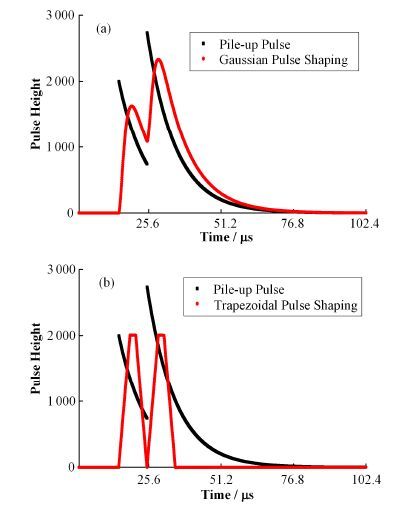
计数率是衡量核测量系统另一个重要指标,其主要受堆积脉冲的影响。通过在第一个核信号结束前叠加相同的核信号,模拟堆积脉冲。分别利用高斯脉冲成形和梯形脉冲成形处理堆积脉冲。模拟核信号的幅度为2V,衰减时间常数为5μs,两种方法得到的成形脉冲达峰时间均为2.5μs,结果如图 6所示。
|
图 6 高斯脉冲成形(a)和梯形脉冲成形(b)分离堆积脉冲 Figure 6 Pile-up pulse separation with Gaussian pulse shaping (a) and trapezoidal pulse shaping (b). |
由图 6可以看出,相同达峰时间条件下,高斯滤波成形不能分离堆积脉冲;梯形脉冲成形算法在分离堆积脉冲的同时,恢复第二脉冲的真实幅度。
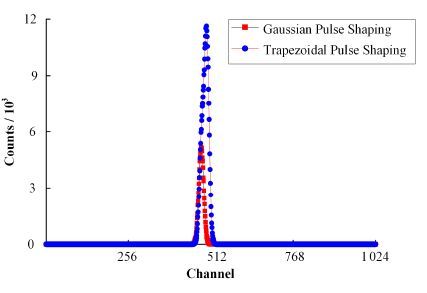
在原始核信号中增加10万个堆积脉冲,采用与§2.2相同方法研究高斯脉冲成形算法在分离堆积脉冲中的应用。高斯脉冲成形参数τ=15,K=2;梯形脉冲成形参数na=30,nb=30,所得幅度谱如图 7所示。由图 7可以看出,采用高斯脉冲成形算法所得幅度谱的总计数明显低于采用梯形脉冲成形算法所得到的幅度谱,梯形脉冲成形算法适用于分离堆积脉冲。
|
图 7 高斯脉冲成形与梯形脉冲成形总计数对比 Figure 7 Comparison of Gaussian pulse shaping and trapezoidal pulse shaping on total counts. |
由§2.2和2.3可以看出,高斯脉冲成形与梯形脉冲成形分别在滤波和堆积脉冲分离中各具优势。结合两者的优点,先利用高斯脉冲成形提高核信号信噪比,然后利用梯形脉冲成形,分离堆积脉冲。从§2中可知,虽然τ值越大对噪声的抑制能力越好,但成形脉冲的宽度增大,易产生堆积脉冲。
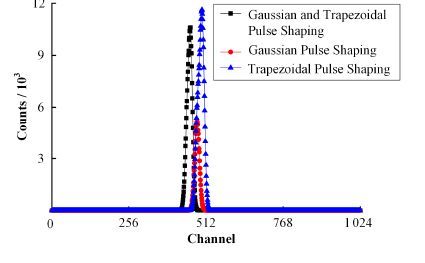
模拟30万个带高斯白噪声的核信号作为原始核信号(其中含有10万个堆积脉冲),先做高斯脉冲成形处理得到高斯脉冲,然后再对高斯脉冲做梯形脉冲成形处理,最后对梯形脉冲做幅度甄别得到幅度谱。高斯脉冲成形参数τ=8,K=2;梯形脉冲成形参数na=30,nb=30,所得幅度谱与单独采用高斯脉冲成形和梯形脉冲成形结果对比如图 8所示。
|
图 8 先高斯脉冲成形再梯形脉冲成形 Figure 8 Performance of Gaussian pulse shaping before trapezoidal pulse shaping. |
不同成形方法所得幅度谱的半高宽与核信号总计数如表 1所示。由表 1可以看出,采用先高斯脉冲成形再做梯形脉冲成形的方法得到的核信号总计数较单独采用高斯成形方法所得总计数提高了2.3倍。在对能量分辨率要求相对较低,而对计数率要求相对较高的应用场合可采用两种滤波成形方法相结合的处理方式。
| 表 1 不同方法得到的半高宽与总计数 Table 1 Total counts and energy resolution with different shaping algorithms. |
在高斯脉冲成形算法基础上,引入了截止频率和品质因子,对成形参数的选择进行了研究。τ与滤波器截止频率有关,τ值越大,对输入信号的高频噪声抑制能力越强,同时增加了成形脉冲宽度;K与输出脉冲品质因子有关,K值越大,成形脉冲品质越高,但尾部出现下冲;当K=2时,输出信号具有最大品质因子。通过与梯形脉冲成形算法对比研究,高斯脉冲成形算法在滤波方面具有更好的噪声抑制能力;梯形脉冲成形算法在堆积脉冲分离方面更具优势。在数字核仪器系统设计时,对采样后的核信号先进行高斯脉冲成形再进行梯形脉冲成形处理可改善系统的计数率,适用于计数率要求相对较高的应用场合。
| [1] |
Jordanov V T, Glenn F. Knoll digital synthesis of pulse shapes in real time for high resolution radiation spectroscopy[J].
Nuclear Instruments and Methods in Physics Research A, 1994, 345 : 337 –345.
DOI: 10.1016/0168-9002(94)91011-1 ( 0) 0)
|
| [2] |
Warburton W K, Momayezi M, Hubbard-Nelson B, et al. Digital pulse processing:new possibilities in nuclear spectroscopy[J].
Applied Radiation and Isotopes, 2000, 53 : 913 –920.
DOI: 10.1016/S0969-8043(00)00247-5 ( 0) 0)
|
| [3] |
Imperiale C, Imperiale A. On nuclear spectrometry pulse digital shaping and processing[J].
Measurement, 2001, 30 : 49 –73.
DOI: 10.1016/S0263-2241(00)00057-9 ( 0) 0)
|
| [4] |
Esmaeili-sani V, Moussavi-zarandi A, Akbar-ashrafi N, et al. Neutron-gamma discrimination based on bipolar trapezoidal pulse shaping using FPGAs in NE213[J].
Nuclear Instruments and Methods in Physics Research A, 2012, 694 : 113 –118.
DOI: 10.1016/j.nima.2012.08.025 ( 0) 0)
|
| [5] |
Regadio A, Sanchez-Prieto S, Prieto M, et al. Implementation of real-time adaptive digital shaping for nuclear spectroscopy[J].
Nuclear Instruments and Methods in Physics Research A, 2014, 735 : 297 –303.
DOI: 10.1016/j.nima.2013.09.063 ( 0) 0)
|
| [6] |
Fernandes A M, Pereira R C, Sousa J, et al. Real time algorithm for digital pulse processing applied to gamma-ray and hard X-ray spectroscopy[J].
Fusion Engineering and Design, 2012, 87 : 2156 –2160.
DOI: 10.1016/j.fusengdes.2012.03.033 ( 0) 0)
|
| [7] |
Hallgren B, Bal F, Barr G, et al. The Na48 LKr calorimeter digitizer electronic chain[J].
Nuclear Instruments and Methods in Physics Research A, 1998, 419 : 680 –685.
DOI: 10.1016/S0168-9002(98)00846-8 ( 0) 0)
|
| [8] |
Pauly S W. Development of a shaping amplifier, gated integrator and 16 K channel ADC for a portable spectroscopy system[J].
Nuclear Instruments and Methods in Physics Research A, 1999, 422 : 379 –384.
DOI: 10.1016/S0168-9002(98)00987-5 ( 0) 0)
|
| [9] |
Gevin O, Lugiez F, Limousin O, et al. IDeF-X V1.0:a new 16-channel low-noise analog front-end for Cd(Zn)Te detectors[J].
Nuclear Instruments and Methods in Physics Research A, 2006, 567 : 140 –144.
DOI: 10.1016/j.nima.2006.05.227 ( 0) 0)
|
| [10] |
Bisello D, Candelori A, Giubilato P, et al. Position sensitive detectors for ion electron emission microscopy[J].
Nuclear Instruments and Methods in Physics Research A, 2007, 573 : 23 –26.
DOI: 10.1016/j.nima.2006.10.268 ( 0) 0)
|
| [11] |
Kalinin A I, Bednyakov V A. Pulse shaping for Ge-spectrometers optimized for ballistic deficit and electronic noise[J].
Nuclear Instruments and Methods in Physics Research A, 2005, 538 : 718 –722.
DOI: 10.1016/j.nima.2004.08.126 ( 0) 0)
|
| [12] |
Fleury J, Taille C L, Martin-Chassard G. Front-end ASICs development for W-Si calorimeter at ILC (CALICE collaboration)[J].
Nuclear Instruments and Methods in Physics Research A, 2007, 572 : 371 –375.
DOI: 10.1016/j.nima.2006.10.223 ( 0) 0)
|
| [13] |
Gómez-Galán J A, López-Ahumada R, SánchezRodríguez T, et al. High speed low power FEE for silicon detectors in nuclear physics applications[J].
Nuclear Instruments and Methods in Physics Research A, 2013, 714 : 155 –162.
DOI: 10.1016/j.nima.2013.03.002 ( 0) 0)
|
| [14] |
陈世国, 吉世印, 刘万松. 基于小波分析的指数衰减信号高斯脉冲成形[J].
物理学报, 2008, 57 (5) : 2882 –2887.
DOI: 10.7498/aps.57.2882 CHEN Shiguo, JI Shiyin, LIU Wansong. Gaussian pulse shaping of exponential decay signal based on wavelet analysis[J]. Acta Physica Sinica, 2008, 57 (5) : 2882 –2887. DOI: 10.7498/aps.57.2882 (  0) 0)
|
| [15] |
陈世国, 吉世印, 刘万松, 等. 基于小波分析的高斯脉冲成形的递归实现[J].
物理学报, 2009, 58 (5) : 3041 –3046.
DOI: 10.7498/aps.58.3041 CHEN Shiguo, JI Shiyin, LIU Wansong, et al. Recursive implementation of Gaussian pulse shaping based on wavelet analysis[J]. Acta Physica Sinica, 2009, 58 (5) : 3041 –3046. DOI: 10.7498/aps.58.3041 (  0) 0)
|
| [16] |
Nakhostin M. Recursive algorithm for real-time digital CR-(RC)n pulse shaping[J].
IEEE Transactions on Nuclear Science, 2011, 58 (5) : 2378 –2381.
DOI: 10.1109/TNS.2011.2164556 ( 0) 0)
|
| [17] |
Zhou J B, Zhou W, Hong X. Improvement of digital S-K filter and its application in nuclear signal processing[J].
Nuclear Science and Techniques, 2013, 24 (6) : 060401 .
DOI: 10.13538/j.1001-8042/nst.2013.06.020 ( 0) 0)
|
