2. 中国科学院大学 北京 100049
2. University of Chinese Academy of Sciences, Beijing 100049, China
作为传统X射线晶体学方法的延伸和发展,相干衍射成像(Coherent Diffraction Imaging,CDI)方法是一种新兴的不依赖于透镜等成像元件的显微成像技术[1]。该方法利用同步辐射装置产生的相干X射线照射非周期性样品,记录样品出射波在自由空间传播至远场所产生的衍射图样强度,并利用相位恢复迭代算法对衍射图样进行相位恢复计算,最后得到样品图像。CDI方法不受成像元件数值孔径和加工精度的限制,可以利用连续弥散的衍射图样对非晶样品成像,其成像分辨率理论上仅受限于X射线的波长及探测器的空间张角。利用同步辐射[1-3]、X射线自由电子激光[4-6]以及小型化的桌面软X射线光源[7-9],CDI方法已经被广泛地应用在材料、生物、环境等研究领域的二维和三维样品成像[10-19]。但是常规CDI方法仅用单幅衍射图样进行相位恢复和图像重建,所以实验过程中必须满足“过采样条件”及分离样品条件[20],即样品尺寸必须小于入射光斑大小且为孤立的。此外,在相位恢复过程中,存在算法收敛慢、重建不收敛或重建停滞、重建结果非唯一等问题[21]。常规平面波CDI在实验数据获取及重建过程中均要求比较高的技巧。
重叠关联成像技术(Ptychography),又称为扫描CDI,是一种由Faulkner[22]和Rodenburg[23]提出的新型CDI方法。它采用一个局域性的照明探针对样品进行扫描,每一个扫描点照明区域与相邻的其它扫描点区域都有部分重叠,每一扫描点产生的远场衍射图样均被记录并用于后续的相位恢复迭代计算中。由于重叠照明区域的样品信息被记录在两幅或者更多的衍射图样中,这使得整套衍射图样中蕴含了大量的相互关联的冗余信息。这些冗余信息不仅可以大大改善相位恢复迭代计算的收敛性,而且可以同时重建样品透射函数和入射探针函数[24-25],并实现衍射图样的延拓外推,对样品进行超分辨成 像[26];求解并弥补实验过程中的不确定因素,比如探针的扫描位置误差[27-29];在不旋转样品的情况下重建三维样品结构[30];重建得到入射光、样品或探测器的混合态信息[31]。
目前,在重叠关联成像实验的图像重建计算中所采用的相位恢复迭代算法一般均把入射光视为空间完全相干的单色光(即单态的入射光),把样品视为稳定平衡的(即单态的样品,非量子多重态并且不存在振动、稳定流动等快速平稳随机过程),把衍射数据采集时间内成像系统所有光学元器件的响应视为固定不变的。这三个条件在实际实验过程中是无法完全保证的。在非理想条件下进行的实验,上述任何一种单态条件发生改变或者出现多重态的混合所造成的退相干效应会使记录的衍射图样变得模糊,进而严重降低重建图像的质量。为在图像重建过程中消除各种来源的混合态效应(退相干效应)所造成的负面影响,本文利用多模式拓展重叠关联迭代引擎(Multi-mode extended Ptychographical Iterative Engine,Mm-ePIE)算法和子像素上采样拓展重叠关联迭代引擎(Sub-pixel Up-sampling extended Ptychographical Iterative Engine,Us-ePIE)算法将实验过程中的混合态效应纳入考虑并对其进行分解,对星型靶实验数据进行处理,然后将两种方法的重建结果进行比较并与单态的拓展重叠关联迭代引擎(extended Ptychographical Iterative Engine,ePIE)算法的重建结果进行对比分析。
1 实验简介 1.1 实验装置及实验参数本文中的X射线重叠关联成像实验在上海同步辐射光源谱学显微线站[32-36](BL08U1A)进行,实验装置如图 1所示。
|
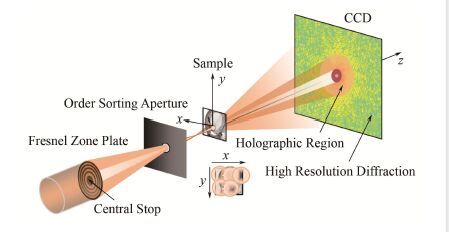
图 1 X射线重叠关联成像方法原理示意图 Figure 1 Schematic of X-ray ptychography. |
BL08U1A束线装置产生的相干X射线被菲涅尔波带片聚焦。聚焦光经过级选光阑的选择,仅允许一级聚焦光通过并照射到样品上,其余的高级次聚焦光(衍射光)均被遮挡。实验过程中通过将样品移动到离焦位置,调整离焦距离,可以获得任意尺寸的探针光斑。探针对样品的重叠扫描示意同样见图 1。实验所采用的样品为购买自美国Xradia公司的标准分辨率测试靶(星型靶),其最中心条纹宽度及间距为30 nm。实验中采用的探针光斑大小为3μm,探针扫描步长为500 nm,扫描点阵为10×10,总共记录100幅衍射图样。
1.2 相位恢复迭代算法 1.2.1 ePIE算法作为重叠关联成像技术目前最常用的相位恢复迭代算法之一,ePIE的详细原理见文献[25],这里只给出主要步骤和相关公式。我们采用r表示实空间坐标;q表示傅里叶空间坐标;$\mathcal{F}$表示傅里叶变换;下标j表示第j个扫描点;Rj表示该扫描点探针与样品的相对位置。每一个扫描位置的迭代更新过程如下:
1) 入射探针函数Pr照射到样品Or上,形成出射波:
| ${{\psi }_{j,r}}={{O}_{j,r}}{{P}_{j,r-{{R}_{j}}}}$ | (1) |
2) 出射波在自由空间传播至远场,形成探测器平面(傅里叶空间)的波前函数:
| ${{\varphi }_{j,q}}=\mathcal{F}\left\{ {{\psi }_{j,r}} \right\}$ | (2) |
3) 该远场波前形成的衍射图样强度分布如下:
| ${{I}_{j,q}}=\left| {{\varphi }_{j,q}} \right|$ | (3) |
4) 利用电荷耦合元件(Charge-coupled Device,CCD)记录的光强度信息$I_{j,q}^{\text{M}}$在傅里叶空间中进行振幅替换,得到更新后的远场波前函数:
| $\varphi _{j,q}^{'}=\sqrt{I_{j,q}^{\text{M}}}\frac{{{\varphi }_{j,q}}}{\sqrt{{{I}_{j,q}}}}$ | (4) |
5) 将振幅替换后的远场波前函数在自由空间反传播至样品平面,得到更新后的样品出射波:
| $\psi _{j,r}^{'}={{\mathcal{F}}^{-1}}\left\{ \varphi _{j,q}^{'} \right\}$ | (5) |
6) 利用新的出射波对样品函数和探针函数进行更新,并作为下一个位置的初始输入:
| ${{O}_{j+1,R}}=O_{j,r}^{'}={{O}_{j,r}}+\alpha \frac{P_{j,r-{{R}_{j}}}^{*}}{\left| {{P}_{j,r-{{R}_{j}}}} \right|_{\max }^{2}}\left( \psi _{j,r}^{'}-{{\psi }_{j,r}} \right)$ | (6) |
| ${{P}_{j+1,R}}=P_{j,r}^{'}={{P}_{j,r}}+\beta \frac{O_{j,r-{{R}_{j}}}^{*}}{\left| {{O}_{j,r-{{R}_{j}}}} \right|_{\max }^{2}}\left( \psi _{j,r}^{'}-{{\psi }_{j,r}} \right)$ | (7) |
式中:a、β为更新弛豫参数,取值范围为0-1。
对所有扫描位置都利用上述步骤对样品函数和探针函数进行更新后,便完成了一步迭代。重复上面的迭代过程直至样品函数和探针函数均收敛至稳定解。
1.2.2 Mm-ePIEePIE算法默认探针、样品、成像系统响应均是单态的。文献[31]给出了基于多相干模式分解的将探针混合态和样品混合态均纳入到重建算法中的基本原理。本文中由于实验中所采用的标准靶样品不存在量子多重态,可以当作单态样品进行处理。我们只考察入射探针的混合态对重建质量的影响,将样品单态简化后,多模式算法的迭代更新过程如下:
1) 由多个相互正交的单模成分{$P_{r}^{1}$,$P_{r}^{2}$,…,$P_{r}^{k}$,… }构成的入射探针照射到样品上,每个单模式成分形成的出射波为:
| $\psi _{j,r}^{k}={{O}_{j,r}}P_{j,r-{{R}_{j}}}^{k}$ | (8) |
2) 出射波在自由空间传播至远场,在探测器平面(傅里叶空间)每个单模式(单态)形成的波前函数:
| $\varphi _{j,q}^{k}=\mathcal{F}\left\{ \psi _{j,r}^{k} \right\}$ | (9) |
3) 所有单态成分共同形成的衍射图样强度 如下:
| ${{I}_{j,q}}=\sum\limits_{k}{{{\left| \varphi _{j,q}^{k} \right|}^{2}}}$ | (10) |
4) 每个单态的远场波前在傅里叶空间振幅 替换:
| $\varphi _{j,q}^{{{k}'}}=\sqrt{I_{j,q}^{\text{M}}}\frac{\varphi _{j,q}^{k}}{\sqrt{{{I}_{j,q}}}}$ | (11) |
5) 将振幅替换后的远场波前在自由空间反传播至样品平面:
| $\psi _{j,r}^{{{k}'}}={{\mathcal{F}}^{-1}}\left\{ \varphi _{j,q}^{{{k}'}} \right\}$ | (12) |
6) 利用新的出射波对样品函数和每一个单态成分探针函数进行更新,并作为下一个位置的初始输入:
| $O_{j+1,r}^{{}}=O_{j,r}^{{}}+\alpha \frac{\sum\limits_{k}{P_{j,r-{{R}_{j}}}^{k*}}\left( \psi _{j,r}^{{{k}'}}-\psi _{j,r}^{k} \right)}{{{\left( \sum\limits_{k}{\left| P_{j,r-{{R}_{j}}}^{k} \right|_{{}}^{2}} \right)}_{\max }}}$ | (13) |
| $P_{j+1,r}^{k}=P_{j,r}^{k}+\beta \frac{O_{j,r+{{R}_{j}}}^{*}}{\left| {{O}_{j,r+{{R}_{j}}}} \right|_{\text{max}}^{2}}\left( \psi _{j,r}^{{{k}'}}-\psi _{j,r}^{k} \right)$ | (14) |
另外,我们给出利用施密特正交化方法将初始探针所有相干模式进行正交化的公式。假设{$E_{r}^{1}$,$E_{r}^{2}$,…,$E_{r}^{k}$,… }是没有进行正交化的初始探针函数,那么有:
| $\begin{matrix} P_{r}^{1}=E_{r}^{1} \\ P_{r}^{2}=E_{r}^{2}-\frac{E_{r}^{2}\cdot P_{r}^{1}}{P_{r}^{1}\cdot P_{r}^{1}}P_{r}^{1} \\ \cdots \\ P_{r}^{k}=E_{r}^{k}-\frac{E_{r}^{k}\cdot P_{r}^{1}}{P_{r}^{1}\cdot P_{r}^{1}}P_{r}^{1}-...-\frac{E_{r}^{k}\cdot P_{r}^{k-1}}{P_{r}^{k-1}\cdot P_{r}^{k-1}}P_{r}^{k-1} \\ \cdots \\ \end{matrix}$ | (15) |
所以,{$P_{r}^{1}$,$P_{r}^{2}$,…,$P_{r}^{k}$,… }即是正交化了的初始探针函数。
1.2.3 Us-ePIE另外一种可进行等效混合态分解的相位恢复迭代算法是子像素上采样方法[37]。该方法最初被提出来用于解决实验中探测器像素尺寸过大,不满足过采样条件的问题。它构造一个虚拟的像素尺寸更小的子像素探测器,每n×n个子像素对应实际探测器的一个像素。在相位恢复迭代算法中,除了振幅替代之外,其他步骤均利用与子像素探测器阵列相同尺寸的矩阵进行;而在振幅替代步骤,n×n个子像素的强度和被用来做替换。亦即将ePIE算法步骤(4)中的式(4)更换为:
| $\varphi _{j,q,{{q}_{s}}}^{'}=\sqrt{I_{j,q}^{M}}\frac{{{\varphi }_{j,q,{{q}_{s}}}}}{\sqrt{\sum\limits_{{{q}_{s}}}{{{I}_{j,q,{{q}_{s}}}}}}}$ | (16) |
式中:qs表示单个像素对应的子像素矩阵。因此每一个实际像素对应的n×n个子像素的相对强度在图像重建过程中是自由更新发展的。Us-ePIE算法将实验中各种来源的混合态效应在探测器平面(傅里叶空间)的子像素尺度上进行了分解,因此有可能消除混合态的负面影响。
2 实验结果及讨论 2.1 重建结果比较对星型靶实验得到的同一组实验数据采用不同的相位恢复算法进行图像重建,所得样品图像如图 2所示,入射探针的重建结果如图 3所示。其中,三种算法的迭代步数均为500步;迭代循环中的更新弛豫参数(式(6、7、13、14))经过不同的重建测试优化后均设为最优参数α=0.15、β=0.25;Mm-ePIE重建过程采用5个相干模式,它们是随机生成的圆形复数波前,经过施密特正交化之后作为初始入射探针函数输入到算法中;Us-ePIE算法中,子像素矩阵维度为3×3。

|
图 2 采用不同的相位恢复迭代算法得到的样品振幅图像 (a) ePIE,(b) Mm-ePIE,(c) Us-ePIE,(d) SEM图像 Figure 2 Amplitude images of the sample obtained from different algorithms. (a) ePIE,(b) Mm-ePIE,(c) Us-ePIE,(d) SEM |

|
图 3 采用不同的相位恢复算法得到的探针振幅图像 (a) ePIE,(b-f) Mm-ePIE算法,(g) Us-ePIE Figure 3 Amplitude images of the probe(s) obtained from different algorithms. (a) ePIE,(b-f) Mm-ePIE,(g) Us-ePIE |
对比样品的重建图像可知,尽管在ePIE算法获得的重建图像(图 2(a))中,最中心的30 nm条纹能够清晰分辨出来,但是条纹的衬度以及条纹内部和间隙区域的强度均匀性明显比Mm-ePIE算法(图 2(b))和Us-ePIE算法(图 2(c))的重建结果差。由此可见,作为典型的单态相位恢复迭代算法,ePIE算法没有考虑实验中出现的各种来源的混合态效应。这些混合态效应在傅里叶空间的解卷积过程中混叠在了重建样品函数与重建探针函数中,造成重建图像质量的严重下降。
比较Mm-ePIE与Us-ePIE算法的重建样品图像,可以发现Mm-ePIE重建图像的条纹边界更明显和清晰、强度分布更均匀。将两者与星形靶的SEM图像(图 2(d))对比,Mm-ePIE算法对样品中心区域由于加工精度原因而附着的杂质颗粒边界的成像明显比Us-ePIE的结果更清晰。这表明在实验过程中,来源于入射探针部分相干性的混合态效应是最主要的负面影响因素,因此针对探针混合态的Mm-ePIE算法具有更好的重建质量。此外,虽然Us-ePIE在算法设计中并没有专门针对入射探针的混合态进行考虑,但是相对于ePIE算法,它对重建质量的改善也是显而易见的。这说明仅依靠子像素在强度总和约束条件下的自由发展就可以在很大程度上消除入射探针的混合态影响。
图 3比较了三种算法重建得到的探针函数振幅图像,其中图 3(a)为ePIE算法,图 3(b-f)为Mm-ePIE算法的5个入射探针模式的最终重建结果,图 3(g)为Us-ePIE算法的重建结果,所有图像均为对数显示。由于Us-ePIE算法引入了3×3的子像素矩阵,其探针矩阵的尺度亦被扩大了3×3倍。图 3(g)中的白色虚线把得到的探针函数分成了3×3个区域,每个区域的大小跟原始数据的维度以及ePIE与Mm-ePIE算法的探针矩阵维度完全一致。
比较ePIE算法和Mm-ePIE算法的结果,可以发现ePIE算法的重建探针有全范围分布的比较强的背景随机起伏,而Mm-ePIE每一个单态成分的背景起伏小得多。这是因为ePIE算法无法解决的混合态效应,在傅里叶空间的解卷积过程中混叠在了重建探针函数里,同时也再次证明实验过程中探针混合态是影响重建质量的主要负面因素。
比较Mm-ePIE和Us-ePIE算法的结果,发现Us-ePIE得到的重建探针函数出现了多个在实空间(样品平面上)相互分离的、类似局域探针分布的光斑。这些分布在傅里叶空间(探测器平面)起到的作用跟Mm-ePIE中输入的多个单模式探针相似,均是在频域空间中进行非相干叠加。因此,Us-ePIE算法能够分解实验中入射探针的混合态信息,将不同的单态分配到了不同的实空间位置上。此外,Us-ePIE算法得到的探针在4个角落区域没有像
Mm-ePIE算法一样出现高强度分布的不规则光斑。这是因为Us-ePIE算法在本质上是把实验中各种来源的混合态效应在子像素尺度上均进行分解表达,因此它除了能够分解探针混合态之外,还能够消除诸如CCD探测器响应或者其他成像系统元件产生的退相干(混合态)效应。而Mm-ePIE算法是专门针对来源于探针和样品的混合态效应而设计的,无法直接解决其他来源的退相干影响,因此在重建探针函数中可能会造成虚假信息分布。
2.2 讨论综合上述对重建结果的系统比较可知,单态ePIE算法的重建样品图像和重建探针函数质量最差,任何来源的混合态效应都会造成其质量的显著下降;Mm-ePIE算法在分解入射探针的混合态方面作用非常明显,能够显著提高采用了部分空间相干X射线入射实验条件下的重建样品图像的质量,但是成像系统中其他来源的混合态效应仍旧会影响重建探针函数的质量;Us-ePIE算法本身不针对特定来源的混合态效应(退相干效应),能够在不同程度上分解各种来源的混合态效应,但是对于入射探针存在混合态时的重建图像质量提升作用,不如Mm-ePIE算法显著。
另外需要指出的是,虽然理论上采用更多的光斑模式或者采用更大的子像素上采样矩阵可以获得更高质量的重建图像,但是重叠关联成像技术实验中采用的入射光的相干性一般是有一定保证的,采用有限的光斑模式或者子像素上采样矩阵可以充分分解实验中出现的非相干因素,获得足够理想的重建结果。进一步增加光斑模式或者子像素上采样矩阵并不能提高重建质量,反而会增加重建的计算量。这也是本文采用5个光斑模式和3×3的子像素上采样矩阵维度的原因。
3 结语本文利用标准样品的实验数据,考查了如何利用混合态分解算法提高扫描CDI重建图像质量的问题,对比了单态ePIE算法、多模式Mm-ePIE算法和上采样Us-ePIE算法三种不同的相位恢复迭代算法的重建样品图像与重建探针函数。实验结果表明,将实验中出现的混合态效应纳入考虑并在相位恢复过程中进行分解能够显著提高重建图像的质量,并且发现多模式算法对入射光部分相干性的分解效应要优于上采样算法。希望在重叠关联成像技术的后续发展中能够出现精确分解各种混合态效应/退相干效应的全新算法。
| [1] |
Miao J W, Charalambous P, Kirz J, et al. Extending the methodology of X-ray crystallography to allow imaging of micrometre-sized non-crystalline specimens[J].
Nature, 1999, 400 (6742) : 342 –344.
DOI: 10.1038/22498 ( 0) 0)
|
| [2] |
Miao J, Ishikawa T, Johnson B, et al. High resolution 3D X-ray diffraction microscopy[J].
Physical Review Letters, 2002, 89 (8) : 088303 .
DOI: 10.1103/PhysRevLett.89.088303 ( 0) 0)
|
| [3] |
Shapiro D, Thibault P, Beetz T, et al. Biological imaging by soft X-ray diffraction microscopy[J].
Proceedings of the National Academy of Sciences of the United States of America, 2005, 102 (43) : 15343 –15346.
DOI: 10.1073/pnas.0503305102 ( 0) 0)
|
| [4] |
Chapman H N, Barty A, Bogan M J, et al. Femtosecond diffractive imaging with a soft-X-ray free-electron laser[J].
Nature Physics, 2006, 2 (12) : 839 –843.
DOI: 10.1038/nphys461 ( 0) 0)
|
| [5] |
Mancuso A P, Schropp A, Reime B, et al. Coherent-pulse 2D crystallography using a free-electron laser X-ray source[J].
Physical Review Letters, 2009, 102 (3) : 035502 .
DOI: 10.1103/PhysRevLett.102.035502 ( 0) 0)
|
| [6] |
Martin A V, Loh N D, Hampton C Y, et al. Femtosecond dark-field imaging with an X-ray free electron laser[J].
Optics Express, 2012, 20 (12) : 13501 –13512.
DOI: 10.1364/OE.20.013501 ( 0) 0)
|
| [7] |
Sandberg R L, Paul A, Raymondson D A, et al. Lensless diffractive imaging using tabletop coherent high-harmonic soft-X-ray beams[J].
Physical Review Letters, 2007, 99 (9) : 098103 .
DOI: 10.1103/PhysRevLett.99.098103 ( 0) 0)
|
| [8] |
Sandberg R L, Song C Y, Wachulak P W, et al. High numerical aperture tabletop soft X-ray diffraction microscopy with 70-nm resolution[J].
Proceedings of the National Academy of Sciences of the United States of America, 2008, 105 (1) : 24 –27.
DOI: 10.1073/pnas.0710761105 ( 0) 0)
|
| [9] |
Ravasio A, Gauthier D, Maia F R N C, et al. Single-shot diffractive imaging with a table-top femtosecond soft X-ray laser-harmonics source[J].
Physical Review Letters, 2009, 103 (2) : 028104 .
DOI: 10.1103/PhysRevLett.103.028104 ( 0) 0)
|
| [10] |
Jiang H, Ramunno-Johnson D, Song C, et al. Nanoscale imaging of mineral crystals inside biological composite materials using X-ray diffraction microscopy[J].
Physical Review Letters, 2008, 100 (3) : 038103 .
DOI: 10.1103/PhysRevLett.100.038103 ( 0) 0)
|
| [11] |
Schroer C G, Boye P, Feldkamp J M, et al. Coherent X-ray diffraction imaging with nanofocused illumination[J].
Physical Review Letters, 2008, 101 (9) : 090801 .
DOI: 10.1103/PhysRevLett.101.090801 ( 0) 0)
|
| [12] |
Nelson J, Huang X J, Steinbrener J, et al. High-resolution X-ray diffraction microscopy of specifically labeled yeast cells[J].
Proceedings of the National Academy of Sciences of the United States of America, 2010, 107 (16) : 7235 –7239.
DOI: 10.1073/pnas.0910874107 ( 0) 0)
|
| [13] |
Raines K S, Salha S, Sandberg R L, et al. Three-dimensional structure determination from a single view[J].
Nature, 2010, 463 (7278) : 214 –217.
DOI: 10.1038/nature08705 ( 0) 0)
|
| [14] |
Abbey B, Whitehead L W, Quiney H M, et al. Lensless imaging using broadband X-ray sources[J].
Nature Photonics, 2011, 5 (7) : 420 –424.
DOI: 10.1038/nphoton.2011.125 ( 0) 0)
|
| [15] |
范家东, 江怀东. 相干X射线衍射成像技术及在材料学和生物学中的应用[J].
物理学报, 2012, 61 (21) : 218702 .
FAN Jiadong, JIANG Huaidong. Coherent X-ray diffraction imaging and its applications in materials science and biology[J]. Acta Physica Sinica, 2012, 61 (21) : 218702 . (  0) 0)
|
| [16] |
刘海岗, 许子健, 张祥志, 等. 中心挡板对扫描相干X射线衍射成像的影响[J].
物理学报, 2013, 62 (15) : 150702 .
LIU Haigang, XU Zijian, ZHANG Xiangzhi, et al. Influence of central beamstop on ptychographic coherent diffractive imaging[J]. Acta Physica Sinica, 2013, 62 (15) : 150702 . (  0) 0)
|
| [17] |
刘海岗, 许子健, 王春鹏, 等. 同步辐射X射线光斑信息对扫描相干衍射成像的影响[J].
辐射研究与辐射工艺学报, 2013, 31 (6) : 060801 .
DOI: 10.11889/j.1000-3436.2013.rrj.31.060801 LIU Haigang, XU Zijian, WANG Chunpeng, et al. Effects of synchrotron radiation X-ray beam on ptychographic coherent diffractive imaging[J]. Journal of Radiation Research and Radiation Processing, 2013, 31 (6) : 060801 . DOI: 10.11889/j.1000-3436.2013.rrj.31.060801 (  0) 0)
|
| [18] |
Yang W, Huang X, Harder R, et al. Coherent diffraction imaging of nanoscale strain evolution in a single crystal under high pressure[J].
Nature Communications, 2013, 4 : 1680 .
DOI: 10.1038/ncomms2661 ( 0) 0)
|
| [19] |
Zhang J, Fan J D, Zhang J H, et al. Three-dimensional coherent diffraction imaging of Mie-scattering spheres by laser single-orientation measurement[J].
Chinese Physics B, 2015, 24 (9) : 094201 .
DOI: 10.1088/1674-1056/24/9/094201 ( 0) 0)
|
| [20] |
Miao J, Kirz J, Sayre D. The oversampling phasing method[J].
Acta Crystallographica Section D, 2000, 56 (10) : 1312 –1315.
DOI: 10.1107/S0907444900008970 ( 0) 0)
|
| [21] |
Marchesini S, Chapman H N, Hau-Riege S P, et al. Coherent X-ray diffractive imaging:applications and limitations[J].
Optics Express, 2003, 11 (19) : 2344 –2353.
DOI: 10.1364/OE.11.002344 ( 0) 0)
|
| [22] |
Faulkner H M L, Rodenburg J M. Movable aperture lensless transmission microscopy:a novel phase retrieval algorithm[J].
Physical Review Letters, 2004, 93 (2) : 023903 .
DOI: 10.1103/PhysRevLett.93.023903 ( 0) 0)
|
| [23] |
Rodenburg J M, Faulkner H M L. A phase retrieval algorithm for shifting illumination[J].
Applied Physics Letters, 2004, 85 (20) : 4795 –4797.
DOI: 10.1063/1.1823034 ( 0) 0)
|
| [24] |
Thibault P, Dierolf M, Menzel A, et al. High-resolution scanning X-ray diffraction microscopy[J].
Science, 2008, 321 (5887) : 379 –382.
DOI: 10.1126/science.1158573 ( 0) 0)
|
| [25] |
Maiden A M, Rodenburg J M. An improved ptychographical phase retrieval algorithm for diffractive imaging[J].
Ultramicroscopy, 2009, 109 (10) : 1256 –1262.
DOI: 10.1016/j.ultramic.2009.05.012 ( 0) 0)
|
| [26] |
Maiden A M, Humphry M J, Zhang F, et al. Superresolution imaging via ptychography[J].
Journal of the Optical Society of America A, 2011, 28 (4) : 604 –612.
DOI: 10.1364/JOSAA.28.000604 ( 0) 0)
|
| [27] |
Shenfield A, Rodenburg J M. Evolutionary determination of experimental parameters for ptychographical imaging[J].
Journal of Applied Physics, 2011, 109 (12) : 124510 .
DOI: 10.1063/1.3600235 ( 0) 0)
|
| [28] |
Maiden A M, Humphry M J, Sarahan M C, et al. An annealing algorithm to correct positioning errors in ptychography[J].
Ultramicroscopy, 2012, 120 : 64 –72.
DOI: 10.1016/j.ultramic.2012.06.001 ( 0) 0)
|
| [29] |
Zhang F, Peterson I, Vila-Comamala J, et al. Translation position determination in ptychographic coherent diffraction imaging[J].
Optics Express, 2013, 21 (11) : 13592 –13606.
DOI: 10.1364/OE.21.013592 ( 0) 0)
|
| [30] |
Maiden A M, Humphry M J, Rodenburg J M. Ptychographic transmission microscopy in three dimensions using a multi-slice approach[J].
Journal of the Optical Society of America A, 2012, 29 (8) : 1606 –1614.
DOI: 10.1364/JOSAA.29.001606 ( 0) 0)
|
| [31] |
Thibault P, Menzel A. Reconstructing state mixtures from diffraction measurements[J].
Nature, 2013, 494 (7435) : 68 –71.
DOI: 10.1038/nature11806 ( 0) 0)
|
| [32] |
Xue C, Wang Y, Guo Z, et al. High-performance soft X-ray spectromicroscopy beamline at SSRF[J].
Review of Scientific Instruments, 2010, 81 (10) : 103502 .
DOI: 10.1063/1.3491837 ( 0) 0)
|
| [33] |
谭兴兴, 刘海岗, 郭智, 等. 基于上海光源扫描透射X射线显微术的相干衍射成像模拟[J].
光学学报, 2011, 31 (4) : 0418001 .
DOI: 10.3788/AOS201131.0418001 TAN Xingxing, LIU Haigang, GUO Zhi, et al. Simulation of coherent diffraction imaging based on scanning transimission X-ray microscopy of Shanghai Synchrotron Radiation Facility[J]. Acta Optica Sinica, 2011, 31 (4) : 0418001 . DOI: 10.3788/AOS201131.0418001 (  0) 0)
|
| [34] |
祝江威, 许子健, 刘海岗, 等. 基于X射线相干衍射成像的元素分布成像[J].
核技术, 2012, 35 (4) : 245 –250.
ZHU Jiangwei, XU Zijian, LIU Haigang, et al. Three-dimension elemental mapping based on coherent X-ray diffraction imaging[J]. Nuclear Techniques, 2012, 35 (4) : 245 –250. (  0) 0)
|
| [35] |
Yang S M, Wang L S, Zhao J, et al. Developments at SSRF in soft X-ray interference lithography[J].
Nuclear Science and Techniques, 2015, 26 (1) : 010101 .
DOI: 10.13538/j.1001-8042/nst.26.010101 ( 0) 0)
|
| [36] |
Zhang L, Xu Z, Zhang X, et al. Latest advances in soft X-ray spectromicroscopy at SSRF[J].
Nuclear Science and Techniques, 2015, 26 (4) : 040101 .
DOI: 10.13538/j.1001-8042/nst.26.040101 ( 0) 0)
|
| [37] |
Batey D J, Edo T B, Rau C, et al. Reciprocal-space up-sampling from real-space oversampling in X-ray ptychography[J].
Physical Review A, 2014, 89 (4) : 043812 .
DOI: 10.1103/PhysRevA.89.043812 ( 0) 0)
|


