2. 中国科学院过程工程研究所 北京 100190
2. Institute of Process Engineering, Chinese Academy of Sciences, Beijing 100190, China
核能具有绿色、高效、低碳排放和可规模生产的突出优势,目前,核能在世界范围内得到了较大重视,大力发展核能已成为我国能源中长期发展规划的重点。由于钍基熔盐堆具有本征安全性、核燃料长期稳定供应、核废物最小化、物理防核扩散、多用途与灵活性等特点,已经成为第四代反应堆核能系统的6种候选堆型之一,受到了国际上的广泛关注[1-2]。2011年中国科学院设置了4个A类先导专项,其中“未来先进核裂变能”项目包括“钍基熔盐(Thorium Molten Salt Reactor, TMSR)核能系统”、“加速器驱动的次临界堆(Accelerator Driven sub Critical Reactor, ADS)嬗变系统”两大内容。在TMSR项目中,分为固态燃料球床堆(Thorium Molten Salt Reactor-Solid Fuel, TMSR-SF)和液态燃料熔盐堆(Thorium Molten Salt Reactor-Liquid Fuel, TMSR-LF)[3-4]。
控制棒失控抽出事故是一个非常重要的反应性引入事故。反应堆控制系统失效或操作人员失误造成一根控制棒失控提出,堆功率迅速上升,引起堆芯燃料温度上升,影响反应堆安全。因此,开展TMSR-SF控制棒失控抽出事故分析具有重要意义。
本文借鉴了高温气冷堆安全分析程序所采用的物理模型和数学方法,结合FLiBe熔盐的物性参数和经验公式,开发了可用于TMSR-SF反应性事故分析的瞬态分析程序,并开展了TMSR-SF控制棒失控抽出事故分析和敏感性分析,为TMSR-SF的设计和安全分析提供支持。
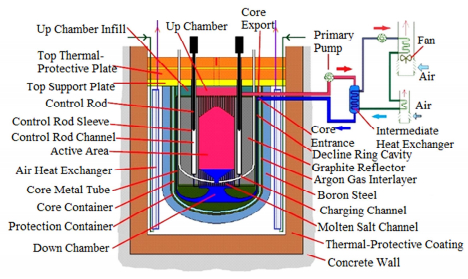
1 TMSR-SF简介TMSR-SF堆芯功率为10 MWt,活性区为圆柱形固定球床堆芯,一次装料11 043颗燃料元件,燃料元件为全陶瓷包覆颗粒球形燃料元件。堆芯活性区体积1.95 m3,堆内包括16根控制棒、一个中子源通道和三个实验测量通道[5-6]。反应堆一回路熔盐为FliBe (LiF-BeF2),二回路熔盐为FliNaK (LiF-NaF-KF)。反应堆一回路由熔盐泵、换热器、反应堆堆芯以及连接管道组成。在正常工况下,堆芯热传递给一回路中的熔盐,通过主换热器,将热量传递给二回路的熔盐,冷却后的一回路熔盐经主熔盐泵送回堆芯,如此循环往复。一回路熔盐进口温度为600 ℃,出口温度为628 ℃,质量流速为41.3 kg·s-1。TMSR-SF系统如图 1所示[7]。
|
图 1 TMSR-SF系统示意图 Figure 1 Schematic of TMSR-SF. |
采用的反应堆系统分析及事故分析程序过程中经常采用的点堆模型来计算堆芯物理参数及堆芯热功率,忽略空间有关的动力学效应,考虑了6组缓发中子的影响。模型如下:
| $\frac{{{\rm{d}}n\left( t \right)}}{{{\rm{d}}t}} = \frac{{\rho \left( t \right)-\beta }}{\Lambda }n\left( t \right) + \sum\limits_{i = 1}^6 {{\lambda _i}{C_i}\left( t \right)} $ | (1) |
| $\begin{array}{c} \frac{{{\rm{d}}{C_i}\left( t \right)}}{{{\rm{d}}t}} = \frac{{{\beta _i}}}{\Lambda }n\left( t \right)-{\lambda _i}{C_i}\left( t \right)\;\;\;\left( {i = 1, 6} \right)\\ \beta = \sum\limits_{i = 1}^6 {{\beta _1}} \end{array}$ | (2) |
式中: n(t)为中子数量;β为缓发中子的总份额;ρ(t)为反应性;Λ为中子代时间;λ为缓发中子衰变常数;C(t)为缓发中子先驱核的浓度;i表示第i组缓发中子。
2.2.2 流体流动传热模型TMSR-SF采用FLiBe熔盐作为其冷却剂,在正常及事故工况下FLiBe熔盐发生沸腾相变的可能很小,因此将其作为单相流体处理。一维单相流体瞬态流动传热的基本控制方程如下。
质量守恒方程:
| $\frac{{\partial \rho }}{{\partial t}} + \frac{\partial }{{\partial z}}\left( {\rho u} \right) = 0$ | (3) |
动量守恒方程:
| $\frac{{\partial \rho u}}{{\partial t}} + \frac{\partial }{{\partial z}}\left( {\rho {u^2}} \right) =-\frac{{\partial p}}{{\partial z}}-\rho g-\Delta {p_f} - \Delta {p_r}$ | (4) |
能量守恒方程:
| $\frac{{\partial \left( {\rho h} \right)}}{{\partial t}} + \frac{{\partial \left( {\rho hu} \right)}}{{\partial z}} = q + \frac{{\partial p}}{{\partial t}}$ | (5) |
式中: ρ为流体密度;u为流体速度;p为流体压力;h为流体焓值;q为壁面传热量;g为重力加速度;Δpf为流体流动时壁面摩擦压降;Δpr为流体流动时局部压降;z代表流体流动距离;t为时间。
2.2.3 辅助计算方程在求解用以模拟上述瞬态流动传热过程的方程时,还应补充大量的辅助方程或本构方程,其中包括壁面摩擦力方程、壁面传热计算方程等。
1) 壁面摩擦力方程
球床堆芯处壁面摩擦力计算采用德国安全导则KTA3102.3规定的公式计算。具体方程如下:
| $\begin{array}{l} \frac{{\Delta P}}{{\Delta z}} = \psi \frac{{1-\varepsilon }}{{{\varepsilon ^3}}}\frac{1}{d}\frac{1}{{2\rho }}{\left( {\frac{m}{A}} \right)^2}\\ \psi = \frac{{320}}{{\left( {\frac{{Re}}{{1-\varepsilon }}} \right)}} + \frac{6}{{{{\left( {\frac{{Re}}{{1-\varepsilon }}} \right)}^{0.1}}}} \end{array}$ | (6) |
固态球床熔盐摩擦力计算采用ERGUN公式:
| $\begin{array}{l} f = \frac{{1-\varepsilon }}{\varepsilon }\left( {a\frac{{1-\varepsilon }}{{Re}} + b} \right)\\ Re = \frac{{md}}{{\mu A}} \end{array}$ | (7) |
2) 壁面传热计算方程
堆芯燃料元件与熔盐冷却剂间的传热过程的计算中采用WAKAO公式:
| $Nu = 2 + 1.1 \times R{e^{0.36}} \times P{r^{1/3}}$ | (8) |
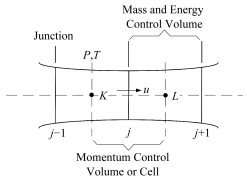
程序中用于流体瞬态传热流动过程、壁面传热过程计算的基本方程均为偏微分方程,无法直接求解,因此采用有限差分方式进行求解。对TMSR-SF的系统特性模拟采用了一维方法,在各瞬态参数(温度、压力等)对空间相离散过程中仅需要将其在流动方向进行离散。在对空间相离散过程中,采用了交错网格技术。交错网格技术中流体物性状态参数和流动参数存放位置不同,相互之间交错半个控制体,即将压力、温度、焓值等物性存放在控制体中心处,而将流体的速度存放在控制体边界处,如图 2所示。对于在控制体边界处的流体物性状态参数采用迎风格式,即采用边界上游控制体的流体物性参数。
|
图 2 网格划分 Figure 2 Grid partitioning. |
1) 质量守恒方程
| $\begin{array}{l} \left( {{\rho _f}} \right)_L^n\frac{{\left( {{\alpha _f}} \right)_L^{n + 1}-\left( {{\alpha _f}} \right)_L^n}}{{\Delta t}} + \left( {{\alpha _f}\frac{{\partial {\rho _f}}}{{\partial P}}} \right)_L^n\frac{{\left( P \right)_L^{n + 1}-\left( P \right)_L^{n + 1}}}{{\Delta t}} + \\ \left( {{\alpha _f}\frac{{\partial {\rho _f}}}{{\partial {T_f}}}} \right)_L^n\frac{{\left( {{T_f}} \right)_L^{n + 1}-\left( {{T_f}} \right)_L^{n + 1}}}{{\Delta t}} + \\ \frac{1}{A}\frac{{\left( {{\alpha _f}{\rho _f}A} \right)_{j + 1}^n - \left( {{\alpha _f}{\rho _f}A} \right)_f^n}}{{\Delta z}} = \left( {{\Gamma _f}} \right)_L^n \end{array}$ | (9) |
2)动量守恒方程
| $\begin{array}{l} \left( {{\alpha _f}{\rho _f}} \right)_j^n\frac{{\left( {{v_f}} \right)_j^{n + 1}- \left( {{v_f}} \right)_j^n}}{{\Delta t}} + \frac{{\left( {{\alpha _f}{\rho _f}v_f^2} \right)_L^n- \left( {{\alpha _f}{\rho _f}v_f^2} \right)_K^n}}{{\Delta z}} = \\ \frac{{\left( {{\alpha _f}} \right)_K^n\left( P \right)_K^{n + 1}- \left( {{\alpha _f}} \right)_L^n\left( P \right)_L^{n + 1}}}{{\Delta z}} - \left( {{\alpha _f}{\rho _f}g\sin \theta } \right)_j^n - \\ \left( {\frac{{\partial F_f^w}}{{\partial z}}} \right)_j^n - \left[{{\Gamma _f}\left( {{v_i}-{v_f}} \right)} \right]_j^n -\left( {\frac{{\partial F_j^i}}{{\partial z}}} \right)_j^n \end{array}$ | (10) |
3) 能量守恒方程
| $\begin{array}{l} \left( {{\alpha _f}{\rho _f}\frac{{\partial {h_f}}}{{\partial P}}} \right)_L^n\frac{{\left( P \right)_L^{n + 1}-\left( P \right)_L^{n + 1}}}{{\Delta t}} + \\ \left( {{\alpha _f}{\rho _f}\frac{{\partial {h_f}}}{{\partial {T_f}}}} \right)_L^n\frac{{\left( {{T_f}} \right)_L^{n + 1}-\left( {{T_f}} \right)_L^{n + 1}}}{{\Delta t}}\\ \left( {{\alpha _f}{h_f}\frac{{\partial {\rho _f}}}{{\partial P}}} \right)_L^n\frac{{\left( P \right)_L^{n + 1}-\left( P \right)_L^{n + 1}}}{{\Delta t}} + \\ \left( {{\alpha _f}{h_f}\frac{{\partial {\rho _f}}}{{\partial {T_f}}}} \right)_L^n\frac{{\left( {{T_f}} \right)_L^{n + 1} - \left( {{T_f}} \right)_L^{n + 1}}}{{\Delta t}} + \\ \left( {{\rho _f}{h_f}} \right)_L^n\frac{{\left( {{\alpha _f}} \right)_L^{n + 1} - {{\left( {{\alpha _f}} \right)}_L}n}}{{\Delta t}} + \\ \frac{1}{A}\frac{{\left( {{\alpha _f}{\rho _f}{v_f}{h_f}A} \right)_{j + 1}^n - \left( {{\alpha _f}{\rho _f}{v_f}{h_f}A} \right)_j^n}}{{\Delta z}}\\ \left( {{\Gamma _f}} \right)_L^{n + 1}\left( {h_f^*} \right)_L^n + \left( {{Q_{wf}}} \right)_L^n + \left( {{Q_{if}}} \right)_L^{n + 1} + \left( {{\Gamma _w}{{h'}_f}} \right)_L^n \end{array}$ | (11) |
由于熔盐堆和高温气冷堆具有相同的燃料元件、相似的堆芯结构、相似的运行温度条件,因此选择高温气冷堆为对象对所开发的程序进行验证,以确定程序的计算精度和正确性。验证计算选择的工况为反应性引入事故,对比的计算结果来自高温气冷堆安全分析报告结果[8]。
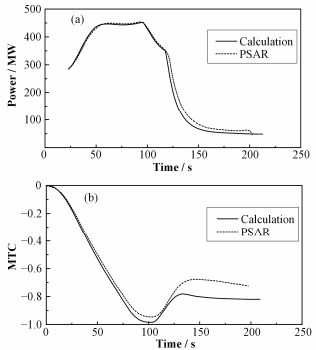
图 3(a)和(b)分别给出了开发程序计算与安全分析报告中得到的高温气冷堆一根控制棒在100%功率运行工况下失控提升事故中堆芯功率、温度反应性(Moderator temperature coefficient, MTC)反馈随时间变化规律。由图 3可知,程序计算结果与安全分析报告结果符合性较好,变化规律也一致,从而验证了程序用于分析TMSR-SF控制棒失控抽出事故的可行性。
|
图 3 功率(a)、反应性(b)随时间变化 Figure 3 Power (a) and MTC (b) vs. time. |
目前TMSR-SF尚处于设计阶段,公开资料及文献中关于TMSR-SF反应堆保护系统动作定值的描述比较少,为更加全面、更加深入地研究和探讨TMSR-SF反应堆的安全特性,在控制棒失控抽出事故分析中,考虑了各反应堆保护系统动作定值、系统设备特性参数(如探测信号响应延迟等)对其事故的影响,具体工况划分见表 1。
| 表 1 工况划分 Table 1 Condition definition. |
针对TMSR-SF控制棒失控抽出事故进行了分析计算所采用的主要假设如下:
1) 初始功率取额定功率,即100%功率;
2) 一根控制棒失控提出堆芯引入的总反应性分别为0.01;
3) 反射层控制棒以1 cm·s-1的速度提出,反应性线性引入;
4) 考虑最长的停堆延迟时间和反应性当量最大的控制棒卡在堆外,控制棒下落引入的总的反应性为0.1;
5) 控制棒落棒时间为5 s。
4.2 结果分析 4.2.1 停堆功率限值的影响如表 1所示,分别假设反应堆中子注量率/反应堆核功率超过额定值20%和30%后延迟1 s触发反应堆紧急停堆。
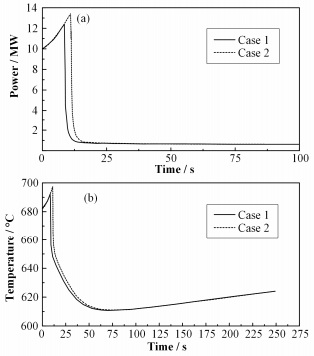
由图 4(a)和(b)可知,控制棒失控抽出事故下反应堆核功率很快达到停堆限值,并触发反应堆紧急停堆。由于控制棒下落速度较快,反应堆功率迅速降低,反应堆在极短时间内实现停堆,有效确保了反应堆的安全性。由于从事故发生至触发反应堆紧急停堆之间的时间较短,反应堆燃料最高温度峰值经历短暂上升后迅速降低,其峰值分别为692.5 ℃和697.6 ℃,远低于1 600 ℃的燃料熔化温度限值。从工况1和2的计算结果对比可以看出,反应堆超功率停堆限值越高,停堆触发时间越晚,堆芯出口冷却剂温度越高,反应堆燃料最高温度峰值越大。
|
图 4 功率(a)和燃料最高温度(b)随时间变化 Figure 4 Power (a) and maximum fuel temperature (b) vs. time. |
对于停堆信号的影响,主要研究了由反应堆高功率限值引起的停堆与反应堆出口温度高引起的停堆(具体见表 1中工况1和3)。由于温度信号的探测和响应时间相对较长,计算中假设反应堆在出口熔盐温度达到整定值后8 s触发紧急停堆。
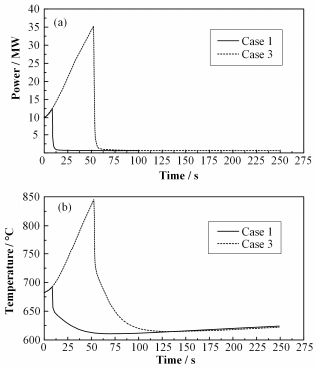
由图 5(a)和(b)可知,堆芯功率和燃料最高温度都呈现先升高后降低的趋势,工况1的燃料最高温度为692.5 ℃,工况3的燃料最高温度846 ℃,低于燃料熔化温度限值。由于控制棒失控抽出事故下反应堆出口熔盐温度达到停堆限值的时间相对较晚,工况3比工况1晚停堆42 s,从而导致工况3中反应堆总的反应性较工况1大,使得堆芯功率和燃料最高温度峰值也相对较大。
|
图 5 功率(a)和燃料最高温度(b)随时间变化 Figure 5 Power (a) and maximum fuel temperature (b) vs. time |
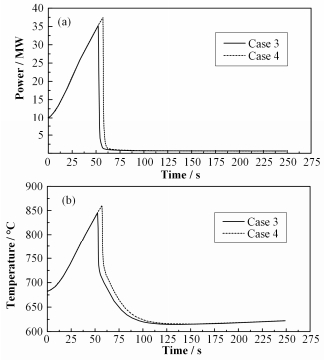
分别选择反应堆出口温度限值为645 ℃(工况3)和650 ℃(工况4)时进行分析。从图 6(a)和(b)可以发现,两种工况下堆芯功率和燃料最高温度变化规律基本一致,均为快速升高达到峰值后迅速下降,两种工况下的燃料温度峰值低于熔化限值。通过对比工况3和4的计算结果可以看出,停堆温度限值越大,停堆触发时间越晚,堆芯出口冷却剂温度峰值越高,反应堆燃料最高温度峰值也越大。
|
图 6 功率(a)和燃料最高温度(b)随时间变化 Figure 6 Power (a) and maximum fuel temperature (b) vs. tim |
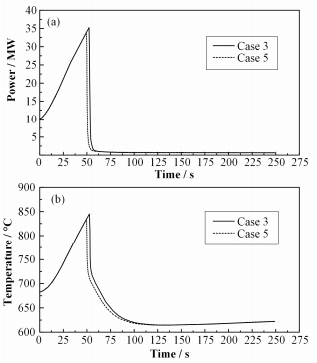
对于延迟时间的影响,分别考虑反应堆温度限值达到延迟时间是8 s和5 s时的情况。由图 7(a)和(b)可知,两种工况下堆芯功率和燃料最高温度变化规律一致,只是随着延迟时间的缩短,堆芯功率和燃料最高温度略有降低。两种工况下的燃料温度峰值低于熔化限值。
|
图 7 功率(a)和燃料最高温度(b)随时间变化 Figure 7 Power (a) and maximum fuel temperature (b) vs. time |
针对TMSR-SF系统,开发了适用于球床式反应堆系统的安全分析软件,并以高温气冷堆为对象对程序计算结果的准确性进行了验证。利用程序对TMSR-SF控制棒失控抽出事故进行了分析计算,研究了其瞬态特性及各停堆信号对其安全性的影响。计算结果表明:
1) TMSR-SF控制棒失控抽出事故下,反应堆功率迅速升高,出口温度和燃料最高温度也随之上升,随着反应堆停堆,功率下降,出口温度和燃料最高温度也迅速下降,最终达到稳定。事故过程中,燃料最高温度远低于1 600 ℃的熔化温度限值。
2) 超功率停堆限值越高,出口温度限值越大,信号延迟时间越长,反应堆停堆越晚,堆芯功率和燃料峰值温度越高。
3) 与超功率停堆限值相比,出口温度限值达到时间更晚,堆芯功率和燃料峰值温度更高。
| [1] |
Ingersoll D T, Forsberg C W, Ott L J, et al. Status of preceonceptual design of the Advanced High-Temperature Reactor (AHTR)[R]. Knoxville, Tennessee:Oak Ridge National Laboratory, ORNL/TM-2004/14, 2004
( 0) 0)
|
| [2] |
Varma V K, Holcomb D E, Peretz F J, et al. AHTR mechanical, structural, and neutronic precocenptual design[R]. Knoxville, Tennessee:Oak Ridge National Laboratory, ORNL/TM-2012/320, 2012
( 0) 0)
|
| [3] |
TMSR研究中心. 2 MWt固态钍基熔盐实验堆概念设计报告(上)[R].上海:中国科学院上海应用物理研究所, 2013
TMSR Research Center. The conceptual design report 2MWt solid thorium-based molten salt experiment reactor (Upper V01)[R]. Shanghai:Shanghai Institute of Applied Physics, Chinese Academy of Sciences, 2013 (  0) 0)
|
| [4] |
田金, 夏晓彬, 彭超, 等. 10-MWt固态钍基熔盐堆乏燃料贮存系统临界安全影响分析[J].
核技术, 2015, 38 (5) : 050602 .
DOI: 10.11889/j.0253-3219.2015.hjs.38.050602 TIAN Jin, XIA Xiaobin, PENG Chao, et al. Impact analysis of criticality safety for 10-MWt solid thorium-based molten salt reactor spent nuclear fuel storage system[J]. Nuclear Techniques, 2015, 38 (5) : 050602 . DOI: 10.11889/j.0253-3219.2015.hjs.38.050602 (  0) 0)
|
| [5] |
TMSR-SFl堆物理分总体. 10 MWt TMSR-SFl总体物理方案和参数[R].上海:中国科学院上海应用物理研究所, 2013
Reactor Physics Department of TMSR-SFI. Physics programs and parameters for 10-MWt TMSR-SF1[R]. Shanghai:Shanghai Institute of Applied Physics, Chinese Academy of Sciences, 2013 (  0) 0)
|
| [6] |
焦小伟, 王凯, 何兆忠, 等. 固态熔盐堆全厂断电ATWS事故工况下的堆芯安全探讨[J].
核技术, 2015, 38 (2) : 020604 .
DOI: 10.11889/j.0253-3219.2015.hjs.38.020604 JIAO Xiaowei, WANG Kai, HE Zhaozhong, et al. Core safety discussion under station blackout ATWS accident of solid fuel molten salt reactor[J]. Nuclear Techniques, 2015, 38 (2) : 020604 . DOI: 10.11889/j.0253-3219.2015.hjs.38.020604 (  0) 0)
|
| [7] |
梅牡丹, 邵世威, 何兆忠, 等. 固态钍基熔盐堆概率安全评价始发事件分析研究[J].
核技术, 2014, 37 (9) : 090601 .
DOI: 10.11889/j.0253-3219.2014.hjs.37.090601 MEI Mudan, SHAO Shiwei, HE Zhaozhong, et al. Research on initial event analysis for solid thorium molten salt reactor probabilistic safety assessment[J]. Nuclear Techniques, 2014, 37 (9) : 090601 . DOI: 10.11889/j.0253-3219.2014.hjs.37.090601 (  0) 0)
|
| [8] |
华能山东石岛湾核电有限公司.华能山东石岛湾核电厂高温气冷堆核电站示范工程初步安全分析报告[R].北京:中国华能集团公司, 2008
Huaneng Shidao Shandong Bay Nuclear Power Co., Ltd. Preliminary safety analysis report on the demonstration project of the high temperature gas cooled reactor nuclear power plant in Shidao Bay, Shandong, China[R]. Beijing:China Huaneng Group, 2008 (  0) 0)
|


