作为缓解严重事故后果的一项重要方案^[1]，通过压力容器外部冷却(External Reactor Vessel Cooling, ERVC)以实现堆内熔融物滞留(In-Vessel Retention, IVR)已经得到了越来越广泛的应用。IVR-ERVC依靠自然循环来对反应堆压力容器(Reactor Pressure Vessel, RPV)壁面进行冷却，带走堆内产生的衰变热，使RPV外壁始终处于较低的温度，从而保持RPV的结构完整性^[1]。当发生堆芯熔化事故时，冷却水从下腔室进入到RPV外壁面和外部保温层之间的冷却通道，对RPV进行冷却，形成的汽水两相流从位于保温层上部的排气孔排出。

目前，围绕IVR-ERVC所开展的研究主要由两部分组成：首先是针对RPV内部熔池结构、壁面换热以及外部冷却能力分析的研究^[2]。其主要目的是保证ERVC的设计具有足够的冷却能力，能够迅速带走堆芯衰变热，防止RPV发生壁面熔毁现象。RPV的外部冷却能力取决于临界热流密度(Critical Heat Flux, CHF)：只有当RPV外壁面的CHF大于内壁面的热流密度时，才有可能保证RPV被充分冷却，而这也是IVR策略成功实施的必要条件。

其次是针对高温条件下RPV壁面蠕变变形所开展的力学研究。其主要目的是分析高温下的RPV壁面的完整性和包容性。对IVR-ERVC技术进行研究的最终目的是防止IVR条件下RPV的失效^[3]。由于高温蠕变断裂是堆芯熔化严重事故下反应堆RPV的主要失效模式，因此大多数与IVR相关的力学研究都以高温蠕变变形为重点。直到现在，对各种材料高温蠕变的研究很难完全通过数值分析实现，所以各国针对蠕变现象陆续开展了一些试验研究^[4]，例如法国原子能总署(Commissariat a I'energie Atomique, CEA)对RPV下封头材料的蠕变和损伤性能进行了试验研究^[5]；美国INEEL (Idaho National Engineering and Environmental Laboratory)对SA533B1钢开展了拉伸和蠕变试验^[6]；瑞典和德国利用RPV缩比模型进行IVR失效试验时得到了多轴蠕变断裂的试验数据^[7]；美国SNL (Sandia National Laboratories)通过RPV下封头失效模拟试验测量出了RPV不同位置上位移与时间的关系^[8]。

目前，虽然针对IVR的研究和应用大多集中在压水堆，但也有针对其他类型核电站开展的IVR研究^[9]。还有一些综述性文献对堆芯熔化条件下反应堆RPV完整性的研究现状进行了总结和归纳^[10]。

在严重事故下，虽然IVR-ERVC可以对RPV外壁面进行冷却，但熔池中的高温熔融物还是会把下封头内壁面加热到很高的温度，使其产生热膨胀和高温蠕变变形。不仅如此，堆芯熔融物还会使部分壁面温度超过材料的熔点温度，造成壁面的熔毁，这会大大降低RPV的壁面厚度，进一步加剧RPV壁面的变形。

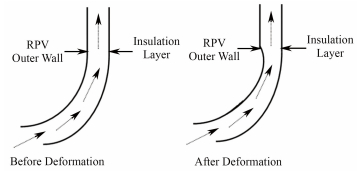
在上述各种因素的共同作用下，RPV外壁面与外部保温层之间的冷却通道会发生变形(图 1)，使CHF与最初的设计值之间产生偏差，这就有可能导致局部传热恶化并造成IVR的失效。而一旦IVR失效，RPV下封头就会被熔穿，其完整性被破坏，进而可能造成放射性物质的外逸。因此，有必要对IVR条件下RPV壁面的变形，以及壁面变形对冷却通道尺寸的影响进行研究。

图 1

图 1 外部冷却通道 Figure 1 External coolant channel.

本文以国内某压水堆核电厂为例，基于该核电厂与IVR-ERVC相关的设计参数，建立数值模型并开展计算分析。由于冷却通道位于RPV外壁面和保温层之间，且保温层的形变可以忽略，所以RPV外壁面的位移就成为影响冷却通道变形的主要因素。

本文首先对RPV外壁面的温度场和力学场进行分析，在此基础上，根据RPV外壁面各点的位移，计算出冷却通道各处的变形大小，为严重事故下RPV外壁面的CHF分析提供必要的输入参数。

本文对反应堆RPV的建模、网格划分、温度场和力学场的分析都使用通用有限元分析软件ANSYS。为了控制计算量，根据RPV的结构特点及载荷特征，将RPV简化为二维轴对称模型。为了保证计算质量，本文主要使用四边形结构化网格，也有少量的三角形网格，网格尺寸约为4mm。

虽然研究对象主要是与熔池接触的RPV下封头部分，但作用在下筒体上的载荷也会对计算结果产生影响，因此对下筒体部分也进行了建模。

数值分析采用间接法，分两步分别对温度场和力学场进行分析：

第一步是温度场分析，采用可以进行热分析的PLANE67单元，计算在最不利工况下RPV壁面的温度分布。根据温度场的计算结果判断是否发生壁面熔化现象，并根据熔毁后的剩余壁面厚度重新对RPV进行建模。

第二步是RPV外壁面的力学分析。这一步需要考虑到高温下热膨胀和蠕变等现象的影响，因此需要将单元类型转化为可以进行蠕变分析的PLANE42单元。根据RPV外壁面各点的位移计算结果，可以推导出冷却通道的变形量，作为RPV外壁面CHF研究的输入，为更加准确地评估RPV外壁面冷却能力提供帮助。

本研究中施加的热学边界条件和载荷包括：

1) 在RPV外壁面施加400 K温度约束。这个温度约束考虑到水的沸点温度和过热度，并保守地假设内壁面热流密度等于外壁面临界热流密度，壁面温度不会降低。如果内壁面热流密度大于外壁面CHF，壁面温度就会不断升高造成RPV被熔穿。

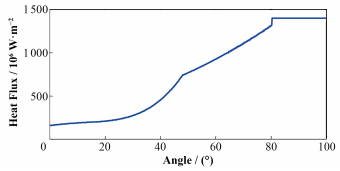
2) 在RPV内壁面输入热流密度包络曲线。RPV内壁面热流密度和事故序列有关，相同事故序列下热流密度曲线也会随时间发生变化。本文采用最严重事故工况中最不利时刻的热流密度曲线(图 2)。图 2中，0°为RPV下封头最底部，90°为下封头和下筒体过渡区，而90°以上为RPV下筒体。

图 2

图 2 压力容器内壁面热流密度 Figure 2 Heat flux of RPV inner wall.

本研究中施加的力学边界条件和载荷包括：

1) 在二维模型对称轴上施加的对称边界条件，在容器上表面施加沿竖直方向的位移约束。

2) 在RPV外壁面施加冷却水的压力。

3) 在RPV内壁面施加堆芯熔融物对壁面的压力。

4) 在RPV内壁面施加1 MPa内压。根据该核电厂的设计，其IVR策略成功的前提之一，就是在堆芯熔化时，通过可靠的多极反应堆冷却剂系统的泄压系统，将RPV内压降低到1 MPa以下。否则，IVR策略将会失效。所以，本文在计算时将内压设定IVR成功实施条件下的最大值1 MPa。

本文所研究的反应堆RPV下筒体及下封头使用的材料牌号是SA-508 GR.3 CL.2。在美国机械工程师协会(American Society of Mechanical Engineers, ASME)标准中没有高温下该材料的性能，也没有关于该材料蠕变性能的数据。因此，本文利用文献[11]中相似材料的性能进行计算。

高温下的材料性能参数，在计算中采用文献[6]中法国牌号16MND5钢（与SA-508 GR.3 CL.2化学成分几乎相同）的高温实验数据。

高温蠕变的参数，在计算中采用文献[11]中SA-533钢（与SA-508 GR.3 CL.2化学成分十分相似）的实验数据。该文献中使用的蠕变公式如下：

式中：$\dot \varepsilon $是应变率；是应变率；σ为应力，MPa；t表示时间，s；C₁ 、C₂和C₃是蠕变参数，其值见表 1。

表 1

表 1 533钢蠕变参数 Table 1 Creep parameters of SA-533. 温度 Temperature/K C1 C2 C3 672.04 1.392×10-23 7.01 -0.757 755.37 3.391×10-15 3.83 -0.595 838.71 8.816×10-15 3.96 -0.376 899.82 3.991×10-12 2.83 -0.164 922.04 4.911×10-9 1.76 -0.436 999.82 1.078×10-7 1.77 -0.322 1 049.82 8.591×10-9 2.66 -0.296 1 149.82 4.090×10-9 3.00 -0.212 1 249.82 4.761×10-8 3.67 -0.464 1 373.15 5.156×10-8 4.74 -0.286

表 1 533钢蠕变参数 Table 1 Creep parameters of SA-533.

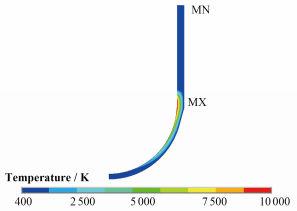
在建立全尺寸RPV壁面模型后，将热学边界条件和热载荷输入到模型中，就可以求出RPV壁面的温度场分布。在实际冷却过程中，RPV壁面温度会随着时间不断变化。本文采用保守的原则，以整个过程中最不利情况下的热流密度包络曲线为输入，计算该条件下的稳态温度场，计算结果如图 3所示。

图 3

图 3 压力容器壁面温度场 Figure 3 Temperature fields of RPV.

计算得到的温度在许多位置超过材料的熔点温度1600K，这些部位会被熔化并造成RPV壁面变薄。在进行力学计算时，壁面厚度变化的影响不能被忽略。本文采取的处理方法是根据温度场的计算结果对RPV重新进行建模。图 4给出了熔堆前后的RPV有限元模型对比。可以看出，部分角度超过80%的壁面厚度被熔毁。

图 4

图 4 堆芯熔毁前后的几何模型 Figure 4 Geometric model of RPV before and after core melt.

利用新建的RPV模型，在施加力学边界条件后，可以得到力学场的分析结果。蠕变造成的塑性形变随时间不断发生变化。计算时基于保守的原则，认为冷却时间为100h，并且在这一过程中RPV内壁面热流密度不会下降。由于本文计算的最终目的是分析RPV壁面膨胀造成的冷却流道变形，所以，对流道形状起直接影响的RPV外壁面位移是重点关注的结果。

计算结果表明，RPV整体位移最小的时刻出现在还没有产生蠕变的初始时刻，此时RPV沿竖直方向膨胀了13.72mm；而位移最大的时刻则出现在蠕变趋于稳定的第100h，此时RPV膨胀达到13.85mm。这表明在IVR条件下，内压为1MPa时，蠕变造成的RPV壁面变形随时间不断增加。

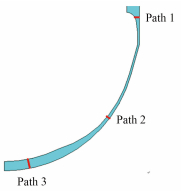
为了进行更深入的力学分析，本文选取三个典型路径，如图 5所示。这三个路径分别位于下封头下筒体的过渡段(Path 1)、下封头中部发生熔壁的位置(Path 2)和下封头底部没有发生熔壁的位置(Path 3)。

图 5

图 5 力学分析路径 Figure 5 Path for mechanical analysis.

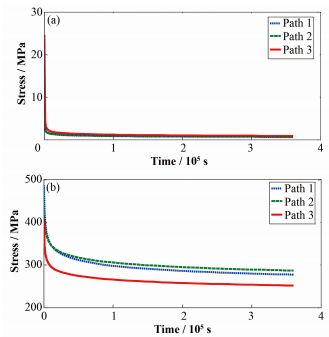
图 6是三个路径内壁和外壁上结点的Von-Mises应力随时间变化的曲线。可以看出在所有路径上，外壁面的应力水平都远大于内壁面，即外壁面承受了大部分的载荷。随着时间的推移，蠕变现象使RPV下封头壁面出现了应力松弛，尤其是在初始时刻最为明显。而在约50h后，应力水平趋于稳定。

图 6

图 6 Von-Mises应力随时间的变化(a)内壁面，(b)外壁面 Figure 6 Evolution of Von-Mises stress. (a) Inner wall, (b) Outer wall

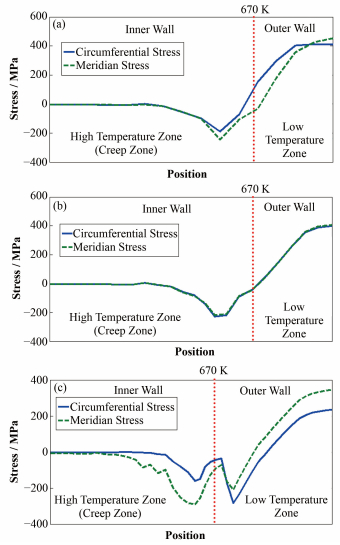
应力松弛现象产生的原因，需要通过观察图 7所示的三个选定路径上的环向应力和子午向应力分布进行解释（径向应力可以忽略）。

图 7

图 7 压力容器壁面应力分布(a)路径1，(b)路径2，(c)路径3 Figure 7 Stress distribution of RPV. (a) Path 1, (b) Path 2, (c) Path 3

需要说明的是低温下RPV的材料不会发生蠕变，只在温度超过约670K时才可能开始产生蠕变变形。在IVR条件下，越靠近内壁面温度越高。因此，高温蠕变只会出现在内壁面温度超过670K的高温区。处于低温区的外壁面不会产生蠕变变形。由于内外壁上应力松弛现象产生的原因并不相同，所以需要分别进行讨论。

图 7中靠近RPV内壁面温度超过670K的高温区几乎全部处于受压状态。高温蠕变现象造成的应力松弛是图 6(a)中内壁结点上压应力随时间降低的原因。

图 7中处于低温区的RPV外壁面大部分处于受拉状态。位于低温区的外壁面结点上，不会产生高温蠕变造成的应力松弛现象。但RPV内部应力平衡会导致外壁面上的拉应力随内壁面压应力水平而降低。这就是图 6(b)中外壁面结点上拉应力随时间减小的原因。

图 7的内壁面受压而外壁面受拉的现象是由内外壁面间的温度梯度造成的：内壁面与高温熔融物接触，接近熔点温度1600K；而外壁面与冷却水接触，温度约400K。1200K的温度梯度导致内壁面上的热膨胀远大于外壁面，因此在壁面上产生较大的热应力。在热应力作用下，形成上述内壁受压而外壁受拉的现象。

事实上，在内压小于1 MPa的情况下，热应力对RPV整体的力学场，尤其是对位移场的影响远大于其他载荷（包括高温蠕变）的作用。通过表 2所示的RPV沿竖直方向整体的变形量可以对这个问题进行说明。

表 2

表 2 压力容器竖直方向整体变形量 Table 2 Total vertical deformation of RPV. 载荷 Load 变形量Deformation /mm 热膨胀 Thermal dilatation 13.11 热膨胀和力学载荷 Thermal dilatation and mechanical load 13.72 热膨胀和蠕变 Thermal dilatation and creep 13.85

表 2 压力容器竖直方向整体变形量 Table 2 Total vertical deformation of RPV.

表 2表明，只考虑热膨胀时，RPV整体沿竖直方向膨胀13.11mm；在此基础上，考虑内压等载荷的作用后，RPV沿竖直方向多膨胀了0.61mm，达到13.72mm；而经过100h蠕变后，RPV沿竖直方向继续膨胀到了13.85mm，并基本保持稳定。由此可见，在IVR条件下，造成RPV变形以及冷却流道变窄的主要因素是热膨胀，高温蠕变断裂尽管是RPV失效的主要模式，但蠕变变形对RPV整体变形的影响远小于热膨胀。

RPV外壁和保温层之间的冷却通道的变形，可以根据计算RPV外壁面沿各角度的膨胀值确定。结果表明，IVR条件下RPV下封头变形造成冷却通道的宽度相比于最初的设计值有所降低，缩减值随位置不同在13.85-18.75mm之间变化，如表 3所示。表 3中，0°为RPV下封头底部，90°为下封头顶部。RPV外壁面与外部保温层之间的外部冷却流道的宽度在90-150mm。也就是说，IVR条件下RPV外壁面的最大变形大约使外部冷却流道的宽度尺寸减少了1/10-1/5。

表 3

表 3 压力容器壁面最大膨胀量 Table 3 Maximum dilatation of RPV. 角度 Angle/(°) 变形量 Deformation/mm 0 13.85 10 14.15 20 14.17 30 15.15 40 18.22 50 18.55 60 15.23 70 14.62 80 16.01 90 18.75

表 3 压力容器壁面最大膨胀量 Table 3 Maximum dilatation of RPV.

通过对IVR条件下RPV下筒体和下封头力学的研究，可以得出以下几点结论：

1) 高温熔池会造成RPV内壁面熔化，并使RPV壁面的厚度显著降低，部分位置上超过80%的壁面厚度被熔毁。

2) 尽管热膨胀不是高温熔堆事故下RPV的主要失效模式，但对RPV壁面变形及冷却通道形状的影响远大于其他因素，包括可能造成断裂失效的高温蠕变。

3) 发生熔堆事故时，如果能够成功实现RPV外部淹没，并将内部压力降低到1 MPa以下，那么RPV内壁面产生高温蠕变的区域大部分处于受压状态，而外壁面没有产生高温蠕变的区域则处于受拉状态。

4)  IVR条件下RPV的最大膨胀值（即冷却通道宽度的最大缩减值）随角度不同在13.85-18.75mm之间变化。