随着核工业的发展,越来越多的核设施投入生产应用,在这些核设施周围存在着不同强度的辐射场。降低操作人员遭受不必要的辐照,以及对核设施进行动态监测,都需要掌握辐射场分布以及变化规律。
虚拟现实技术(Virtual Reality, VR)具有交互性、沉浸性等特点,国内外均已有团队着手开发基于VR的辐射防护系统。将VR应用于辐射防护领域具有诸多优点:辐射场分布以更直观的方式展示出来,加深操作人员对辐射场分布及其变化规律的了解,从而可以设计出更合理的实验方案;同时,操作人员可在仿真辐射场中进行操作练习,在低风险的情况下提高操作的熟练度。目前,国内研究团队已掌握了基于VR的辐射防护系统开发的关键技术,不过对核设施系统的建模及辐射场可视化等方面还存在问题[1]。
辐射场数据获取方式主要包括模拟计算以及实验测量。目前,最常用的模拟计算方法是蒙特卡罗方法,该方法能够获得辐射场多种信息,比如能谱、注量、剂量等,受计算机运算能力以及计算程序运算效率的限制,在某些复杂条件下计算整个辐射场的信息需要花费数小时乃至数天的时间。此外,利用蒙特卡罗方法进行模拟计算,需要对放射源系统的结构信息较为清楚,从而建立准确的系统模型完成粒子输运模拟,对于放射源内部结构未知的情况不适用。在实际应用中,往往通过实验测量获取辐射场数据,尤其当掌握的放射源系统结构信息比较少时。由于测量时间或条件的限制,实际测量整个辐射场的空间分布是不现实的,只能利用有限个采样数据完成辐射场数据重构,这时就需要对这些数据进行插值处理,从而获取更多关于辐射场的信息。
根据离散数据在空间中的分布规律,采样数据集合可分为规则点集以及非规则点集。与非规则点集相比,将规则点集过渡至连续空间更容易,只需先将数据按某种顺序连接形成六面体集合,再通过寻找等值面即可,但这样无法避免传统六面体单元的拓扑结构模糊性[2]。对于非规则点集,则需要对这些数据进行四面体剖分后再进行插值处理,虽然过程较复杂,但不仅可以避免拓扑结构模糊性,而且只需要使用少量采样数据即可完成全空间的信息表征。在辐射场可视化过程中,通过实验测量得到的采样数据往往属于非规则点集,对非规则点集进行插值、拟合形成曲线或曲面过程中,需要利用散乱数据插值算法。
早在20世纪60年代,散乱数据插值问题就已经引起了人们的注意,并且也发展出了一系列针对散乱数据插值或逼近的算法,在地形学、测绘学、摄影制图法、地球物理以及产品设计等领域得到广泛应用。目前最常用的中、小规模散乱数据插值算法有三角剖分法、反距离权重插值法、有限元法以及径向基函数插值法等[3]。其中,三角剖分法是最简单的中小规模数据插值方法,但该方法只能实现C0连续,即只可实现数值连续,且对大规模数据剖分效率低[4]。反距离权重插值法中出现最早的是Shepard方法,该方法计算复杂度低,但只能实现C0连续,且在采样数据点附近存在循环以及截断误差[5]。基于有限元的插值方法,在插值过程中不仅需要对数据进行剖分而且包含大量偏导估计工作,运算复杂度高[6]。径向基函数插值算法将一组与方向无关的径向距离作为自变量,通过拓展距离的定义即可直接将算法推广至更高维度的状况[7],且因为其优异的计算精度以及简洁的表达形式,在工程应用中也得到了广泛的应用[8-9]。
多年发展过程中,散乱数据插值方法的结果稳定性以及准确性均得到了充分的验证。综合考虑采样数据大小、插值参数、计算精度等方面因素,与其他中、小规模散乱数据插值算法相比,径向基函数插值算法具有更高的插值可靠性[10]。故我们认为有希望将其应用于辐射场数据重构以及可视化过程中。本文对径向基函数插值算法进行了简述,然后利用Multiquadric散乱数据插值方法,对两种对称属性不同的辐射场重构进行了研究。
1 径向基函数插值算法径向基函数插值方法的基本思想为:利用与距离无关的径向距离作为自变量函数组,计算各点权重,并利用采样点数值,从而完成全局范围内插值重构。
径向基函数插值算法问题可描述为:当给定有限点集(xi, yi)∈Ω,以及相应的值z∈R,其中i=1, 2, …, n,Ω⊂R2是平面的一个界限域,要构造一个曲面f:Ω→R的基本形式为:
| $f\left( {x, y} \right) = \sum\limits_{i = 1}^n {{\alpha _i}\phi \left( {{r_i}} \right)} $ | (1) |
同时满足条件:
| $f\left( {{x_i}, {y_i}} \right) = {z_i}$ | (2) |
式(1)中:ϕ(r)为径向基函数,常用[11-12]的形式有:
Gauss分布函数ϕ(r)=e-c2r2;
Markoff分布函数ϕ(r)=e-c|r|;
Multiquadric函数ϕ(r)=(r2+c2)μ;
逆Multiquadric函数ϕ(r)=(r2+c2)-μ;
幂函数紧支撑基函数ϕ(r)=ϕs, k(r)。
其中,Multiquadric方法[13]是目前应用最成功的径向基函数插值算法之一,因其形式简单、计算精度高,该方法在地形学、水力学、测地学、地球物理以及地壳运动等领域得到成功运用。综合考虑γ辐射场分布特点以及计算复杂度,本文选择逆Multiquadric函数为基函数对γ辐射场模拟数据进行插值重构。
2 可视化结果分析 2.1 轴对称的γ辐射场考虑轴对称的情况,对带屏蔽的137Cs点源用蒙特卡罗方法模拟NaI(Tl)探测器测量的计数率空间分布[13-14]。测量系统如下:点源置于原点,距离源2 cm处放置一直径为8 cm、厚度为2 cm的圆形铁片,30 cm处为一个NaI(Tl)探测器,模拟计算模型见图 1。

|
图 1 蒙特卡罗方法模拟计算模型 Figure 1 Monte Carlo simulation model. |
一维Multiquadric方法插值公式如下[15]:
| $C = \sum\limits_{j = 1}^n {{\alpha _j}\sqrt {{{\left( {D-{D_j}} \right)}^2} + \Delta } } $ | (3) |
式中:D为探测角度;C为计数;n为采样点个数;Δ为非负参数。
为考察n、Δ对结果的影响,选取不同n、Δ值,利用Multiquadric方法对模拟数据进行插值处理,插值结果与模拟数据之间的平均相对误差随n、Δ的变化如图 2所示。

|
图 2 平均相对误差随采样数据点个数n (a)和常数Δ (b)的变化 Figure 2 Average relative error as a function of number of sampling data n (a) and constant Δ (b). |
由图 2(a)可知,随着采样数据点个数的增加,平均相对误差呈减小趋势,但减小速度越来越慢。图 2(b)中,平均相对误差随常数Δ增加而先减小再增大,并在
选取8个采样数据点,使用Multiquadric方法(
|
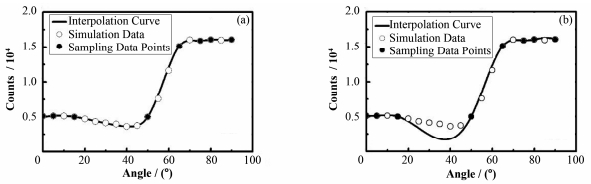
图 3 使用Multiquadric方法(a)和Spline方法(b)的NaI(Tl)探测器不同探测角度下的计数 Figure 3 Counts of NaI(Tl) detector in different angles obtained by Multiquadric method (a) and Spline method (b). |
对于单个137Cs点源,其γ辐射场空间分布各向同性。圆形屏蔽片的加入,使得计数率发生变化。随着探测器与Z方向夹角的增大,到达探测器光子穿过屏蔽片厚度也增加,探测器计数率随之减小,当光子穿过屏蔽片厚度最大(约为38°)时,计数率取得最小值。随后计数率增大,直到到达探测器光子均不通过屏蔽片(约为71°)时,计数率达到最大值。图 3中的模拟数据随着探测器与Z方向夹角增大,计数率先减小后增大,约在40°处取得最小值,大于70°之后计数率不再增加,模拟结果符合预期。选取相同的采样数据点,应用Multiquadric方法得到的插值结果在全区间内与模拟数据符合状况良好。Spline方法插值结果在15°-50°区间曲线与模拟数据存在明显偏差。Multiquadric方法插值结果平均相对误差为1.13%,Spline方法插值结果平均相对误差为11.93%,前者只相当于后者的9.47%,可见Multiquadric方法得到的插值结果在全插值区间内与模拟数据符合得更好。
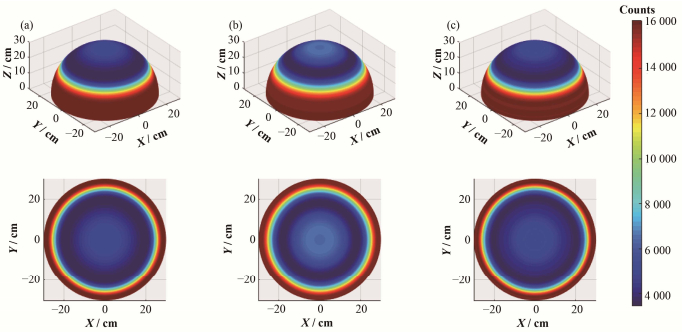
为展示γ辐射场空间分布,利用Multiquadric方法、Spline方法进行数据重构后,得到γ光子计数率空间分布,见图 4(a)及(b)。与图 4(c)利用模拟数据直接绘制得到结果相比,Spline方法得到的可视化结果,即图 4(b)中心区域出现明显差异,而Multiquadric方法得到结果图 4(a)则与模拟结果更相似。所以认为使用Multiquadric方法进行数据重构可以得到比Spline方法更符合预期的结果。
|
图 4 Multiquadric方法(a)、Spline方法(b)和模拟数据(c)得到的距离源30 cm球面γ光子计数分布 Figure 4 Gamma radiation field distribution obtained by Multiquadric method (a), Spline method (b) and simulation data (c). |
考虑转动π/2对称的情况,对带屏蔽的137Cs点源用蒙特卡罗方法模拟NaI(Tl)探测器测量的计数率空间分布。模拟测量系统与图 1类似,不同的是距离源2 cm处放置一个边长为6 cm、厚度为2 cm的方形铁片。
三维Multiquadric插值方法公式如下[15]:
| $C = \sum\limits_{j = 1}^n {{\alpha _j}\sqrt {{{(x - {x_j})}^2} + {{(y - {y_j})}^2} + {{(z - {z_j})}^2} + \Delta } } $ | (4) |
式中:
利用与前文相似的方法,得到单根经线上插值结果与模拟数据之间的平均相对误差随Δ、n变化的规律。我们认为,综合考虑精度以及时间成本,当Δ=35、每条经线(球面上与x、y轴夹角相同的曲线)上采样数据点个数n=5时,插值重构结果最优。为重建整个γ辐射场,使用了45°范围内的10条经线上模拟数据,故总采样数据点个数为50。为展示γ辐射场空间分布,利用Multiquadric方法进行数据重构后,得到γ光子计数率空间分布,平均相对误差为2.79%,其中最大相对误差为24.20%。π/4范围内,各点相对误差见图 5(a)。插值区域边界处相对误差较大,这是由于采样数据选取标准是每条经线上插值结果平均相对误差最小。在实际插值过程中,采样数据点会对周围区域内各条经线的插值结果产生影响。考虑到边界区域内的采样数据密度较低,所以插值结果的相对误差也会比较大。
|
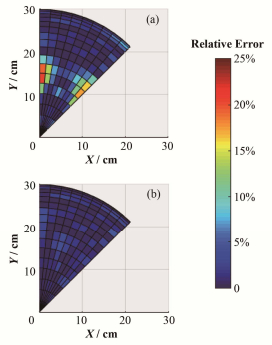
图 5 采样数据优化前(a)和优化后(b)的重构结果相对误差 Figure 5 Average relative error of reconstruction before (a) and after (b) sampling data points optimization. |
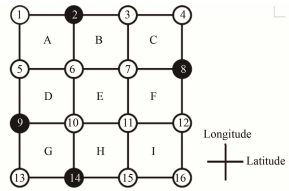
为充分发挥散乱数据插值方法的优势,并进一步提高重构结果的精度,我们提出了一种优化采样数据选取的方案,如图 6所示。图 6中,数字(1, 2, …, 16)代表离散数据点,数值大小等于插值结果与模拟数据之间的相对误差,其中实心点代表已被选取的采样数据点;字母(A, B, …, I)代表周围4个顶点的平均相对误差,其数值由相邻4个顶点的平均值确定。采样数据优化过程如下:
|
图 6 采样数据优化选择原理 Figure 6 Principle of optimized method of sampling data. |
第一步:E代表的区域内的插值精度最低,即全局范围内方块E的数值最大,则移入数据应为点6、7、10、11中之一;第二步:综合考虑A、C、G、I的数值大小,确定移入数据,如4个方块中A的数值最大,则移入数据应为点6;第三步:当移入数据为点6时,移出数据应为点6所在经线上已被选取的采样数据点,即点2或14;第四步:选择对周围影响更小的采样数据点为移除数据;第五步:重复以上步骤,直至达到误差要求。
按以上原则优化采样数据后,π/4范围内插值重构结果与模拟数据相对误差分布见图 5(b)。优化后,区域内平均相对误差为0.99%,与优化前相比降低了64.51%;最大相对误差为6.59%,与优化前相比降低了72.77%。可见,按此方案优化后最大相对误差以及平均相对误差均有显著提高。
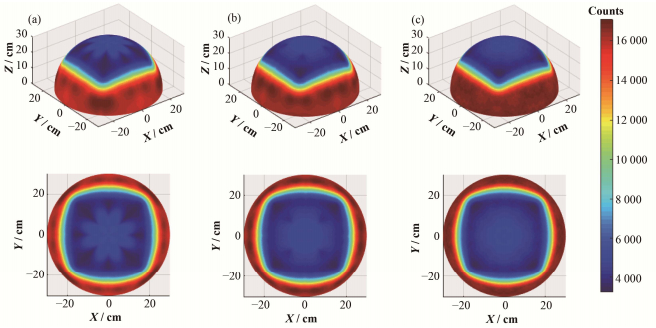
对于单个137Cs点源,其γ辐射场空间分布各向同性,方形屏蔽片的加入使得辐射场分布呈π/2对称,且在与x轴夹角为45°、135°、225°、315°处出现尖角。基于模拟数据直接绘制的γ光子计数率可视化分布结果见图 7(c)。
|
图 7 采样数据选取优化前(a)、优化后(b)和模拟数据(c)得到的距离源30 cm球面γ光子计数分布 Figure 7 Gamma radiation field distribution obtained by before (a), after (b) sampling data points optimization and simulation data (c). |
按采样数据选取优化方案进行优化前、后γ光子计数率空间分布见图 7(a)、(b),均与模拟数据直接绘制的图 7(c)相似。未按方案进行优化时,插值边界处相对误差较大,可视化结果的中心区域出现不规则亮斑。采样数据优化后,该现象明显减弱可视化结果与模拟数据更吻合。可见采样数据优化方案可显著提高数据重构结果精度。
3 结语综合考虑散乱数据插值算法的可靠度、时间效率以及复杂程度,结合γ辐射场特点,本文选取Multiquadric散乱数据插值方法,首次将其应用于γ辐射场空间分布的重构。以两种不同对称属性的辐射场为例,利用少量采样数据点,分别实现了γ辐射场空间分布重构以及可视化。对于具有轴对称性的γ辐射场,与数据分析处理软件MATLAB中Spline插值算法相比,Multiquadric插值方法得到结果的平均相对误差更小,只有1.13%,为前者的9.47%。对于转动π/2对称的γ辐射场,采样数据优化后利用Multiquadric插值方法重构得到的结果从之前的2.79%降为0.99%,降低了64.51%,其中,最大相对误差降低了72.77%。
通过对以上两种具有不同对称属性的γ辐射场进行重构后,我们认为Multiquadric径向基函数插值算法可以应用于辐射场数据重构及可视化过程中,并且在重构精度以及效率等方面均有不俗表现。此后,我们将会利用实验测量得到的数据完成γ辐射场数据重构及可视化研究,以期验证散乱数据插值方法在辐射场重构及可视化领域的应用效果。
| [1] |
王晓静.虚拟现实技术在核电站辐射防护中的应用研究[D].合肥:合肥工业大学, 2010. DOI:10.7666/d.y1700273
WANG Xiaojing. Research on application of VR technology in radiation protection[D]. Hefei:Hefei University of Technology, 2010. DOI:10.7666/d.y1700273 (  0) 0)
|
| [2] |
Lorensen W E, Cline H E. Marching cubes:a high resolution 3D surface construction algorithm[C]. ACM Siggraph Computer Graphics, ACM, 1987, 21(4):163-169. DOI:10.1145/37402.37422
( 0) 0)
|
| [3] |
殷浩, 戴光明. 散乱数据可视化研究综述[J].
微机发展, 2005, 15 (7) : 7 –10.
DOI: 10.3969/j.issn.1673-29X.2005.07.003 YIN Hao, DAI Guangming. Study on visualization of scattered data[J]. Microcomputer Development, 2005, 15 (7) : 7 –10. DOI: 10.3969/j.issn.1673-29X.2005.07.003 (  0) 0)
|
| [4] |
Shepard D. A two-dimensional interpolation function for irregularly spaced data[C]. Proceedings of the 1968 23rd ACM National Conference, ACM, 1968:517-524
( 0) 0)
|
| [5] |
Buhmann M D.
Radial basis functions:theory and implementations[M]. Cambridge University Press, 2003 : 4 .
( 0) 0)
|
| [6] |
张文波, 曹耀钦, 孙伟. 基于有限元插值方法的电磁覆盖范围重建[J].
计算机仿真, 2013, 30 (7) : 170 –173.
DOI: 10.3969/j.issn.1006-348.2013.07.038 ZHANG Wenbo, CAO Yaoqin, SUN Wei. Electromagnetic wave coverage area reconstruction based on finite element interpolation[J]. Computer Simulation, 2013, 30 (7) : 170 –173. DOI: 10.3969/j.issn.1006-348.2013.07.038 (  0) 0)
|
| [7] |
陈堃.空间散乱分布位场数据插值研究[D].杭州:浙江大学, 2013
CHEN Kun. A study on interpolation method for 3D scattered potential field data[D]. Hangzhou:Zhejiang University, 2013 (  0) 0)
|
| [8] |
刘溢浪, 张伟伟, 蒋跃文, 等. 一种基于增量径向基函数插值的流场重构方法[J].
力学学报, 2014, 46 (5) : 694 –702.
DOI: 10.6052/0459-1879-14-028 LIU Yilang, ZHANG Weiwei, JIANG Yuewen, et al. A reconstruction method for finite volume flow field solving based on incremental radial basis function[J]. Chinese Journal of Theoretical and Applied Mechanics, 2014, 46 (5) : 694 –702. DOI: 10.6052/0459-1879-14-028 (  0) 0)
|
| [9] |
Estruch O, Lehmkuhl O, Borrell R, et al. A parallel radial basis function interpolation method for unstructured dynamic meshes[J].
Computers & Fluids, 2013, 80 (7) : 44 –54.
DOI: 10.1016/j.compfluid.2012.06.015 ( 0) 0)
|
| [10] |
Franke R. Scattered data interpolation:tests of some methods[J].
Mathematics of Computation, 1982, 38 (38) : 181 –181.
DOI: 10.2307/2007474 ( 0) 0)
|
| [11] |
朱文文.基于随机径向基函数的散乱数据插值方法[D].大连:辽宁师范大学, 2009. DOI:10.7666/d.y1600762
ZHU Wenwen. Scattered data interpolation with random radical basis functions[D]. Dalian:Liaoning Normal University, 2009. DOI:10.7666/d.y1600762 (  0) 0)
|
| [12] |
李乐庆, 康宝生. 基于RBF的散乱点曲面重构[J].
西北大学学报(自然科学版), 2011, 41 (2) : 221 –225.
LI Leqing, KANG Baosheng. RBF-based surface reconstruction from scattered data[J]. Journal of Northwest University (Natural Science Edition), 2011, 41 (2) : 221 –225. (  0) 0)
|
| [13] |
贺军, 杨朝文. 用γ能谱全能峰计数率测量辐射剂量率的方法研究[J].
核技术, 2014, 37 (7) : 070403 .
DOI: 10.11889/j.0253-219.2014.hjs.37.070403 HE Jun, YANG Chaowen. Measurement of γ absorption dose rate through measuring the full energy peak of γ spectrum[J]. Nuclear Techniques, 2014, 37 (7) : 070403 . DOI: 10.11889/j.0253-219.2014.hjs.37.070403 (  0) 0)
|
| [14] |
张连平, 吴伦强, 党晓军, 等. 分层均匀假设求解源非均匀分布技术[J].
核技术, 2014, 37 (2) : 020602 .
DOI: 10.11889/j.0253-219.2014.hjs.37.020602 ZHANG Lianping, WU Lunqiang, DANG Xiaojun, et al. Acquiring the nuclide distribution based on the hypothesis of layered uniform distribution[J]. Nuclear Techniques, 2014, 37 (2) : 020602 . DOI: 10.11889/j.0253-219.2014.hjs.37.020602 (  0) 0)
|
| [15] |
Hardy R L. Multiquadric equations of topography and other irregular surfaces[J].
Journal of Geophysical Research, 1971, 76 (8) : 1905 –1915.
DOI: 10.1029/JB076i008p01905 ( 0) 0)
|


