1993 年,由 ISO、IEC、BIPM、IFCC、IUPAC、 IUPAP、OIML 7 个国际组织共同组成国际测量不 确定度工作组起草制定了 《测量不确定度表示指南》 (简称 GUM) 。为了贯彻 GUM 在我国的实施,由 全国法制计量委员会委托中国计量科学研究院起草 制定了国家计量技术规范《测量不确定度评定与表 示》 (JJF1059-1999)作为我国统一准则对测量结果 及其质量进行评定、表示和比较。
本文通过对原子吸收光谱法测定白砂糖中铜的 测定过程进行分析,找出影响测定结果不确定度的 因素,通过建立数学模型对各个不确定度分量进行 计算,最终给出该法测定结果的合成标准不确定度 和扩展不确定度。
Z2000 原子吸收光谱仪(日本日立) ;FX-2000 电子天平;马弗炉。
铜标准溶液(由国家钢铁材料测试中钢铁研究 总院提供,不确定度为 0.3%,介质为 10%盐酸) ; 硝酸;硝酸(1+4) ;硝酸(0.5%) 。
称取均匀白砂糖样品 1.00~5.00 g, 置于石英或 瓷坩埚中,加 5 mL 硝酸,放置 0.5 h,小火蒸干, 继续加热碳化, 移入马弗炉中, 500℃± 25℃灰化1 h, 取出放冷,再加 1 mL 硝酸浸湿灰分,小火蒸干。 再移入马弗炉中,500℃灰化 0.5 h,冷却后取出, 以 1 mL 硝酸(1+4)溶解 4 次,移入 10.0 mL 容量 瓶中用水稀释至刻度,备用。
取与消化试样相同量的硝酸,按同一方法做试剂空白试验。
用1 mL移液管吸取1 mL 1000 μg/mL铜标准溶 液至 100 mL 容量瓶中,用 0.5%硝酸溶液定容至刻 度,得浓度为 10 μg/mL 标准使用液,再用 10 mL 刻度吸管吸取10 mL浓度为10 μg/mL标准使用液至 100 mL 容量瓶中,用 0.5%硝酸溶液定容至刻度, 得浓度为 1 μg/mL 标准使用液。
吸取 0.0、 2.5、 5.0、 10.0、 15.0、 20.0 mL 1 μg/mL 铜标准使用液,分别置入 25 mL 容量瓶中,用 0.5% 硝酸溶液稀释至刻度,混匀。容量瓶中每毫升分别 相当于 0.0、0.1、0.2、0.4、0.6、0.8 μg 铜。
将处理后的样液、试剂空白液和各铜标准溶液 分别导入调至最佳条件火焰原子化器进行测定[1]。 测定条件:灯电流 3~6 mA,波长 324.8 nm,光谱 通带 0.5 nm,空气流量 9 L/min,乙炔流量 2 L/min, 灯头高度 6 mm,氘灯背景校正。以铜标准溶液含量 和对应吸光度,计算直线回归方程,试样吸收值带 入方程式,经计算求得白砂糖试样中铜含量。
根据上述的实验步骤[1],计算白砂糖中铜含量的数学模型为:

式中:X—白砂糖中铜的含量(mg/kg) ;
ci —第 i份白砂糖的消化液中铜的浓度 (mg/L) ;
mi—第 i 份白砂糖的质量(g) ;
V—白砂糖消化液定容体积(mL) 。
测量不确定度是与测量结果相关联的参数,它合 理地赋予被测值的分散性。 该分散性主要涉及到 A 类 不确定度、B 类不确定度和合成标准不确定度[2]。
(1)A 类不确定度:由测量列结果统计分布计算,用实验标准偏差表征。
(2)B 类不确定度:基于经验或其它信息的概率分布估计出来,用标准偏差表征。
(3)合成标准不确定度:将 A 类不确定度、B类不确定度的平方和开方的方法叠加起来给出合成标准不确定度。
该不确定度分量主要是由白砂糖样品的重复测 定所引入,属于不确定度的 A 类分量。
该不确定度分量主要是由原子吸收光谱仪测定 吸光度的误差引入,属于不确定度的 B 类分量。
该不确定度分量主要是由定容过程中容量瓶本 身及试验温度变化对体积的影响引入,属于不确定 度的 B 类分量。
该不确定度分量主要是由电子天平的使用误差 引入,属于不确定度的 B 类分量。

|
图 1 测定白砂糖中铜含量的不确定度来源 |
对同一白砂糖样品重复测定 10 次, 测量值如表 1。
| 表 1 白砂糖样品测量值 |
由贝塞尔公式求得单次测量标准差 s (ci) 为 (单 位 mg/kg) :
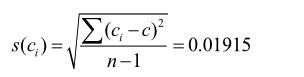
由测量重复性导致的标准不确定度 u(c)为(单位 mg/kg) :

因 此 , 重 复 测 定 的 相 对 标 准 不 确 定 度 为 自由度为 νc = 10 – 1 = 9。
自由度为 νc = 10 – 1 = 9。
由于样品消化不完全或消化过程导致铜损失或 污染等, 将使白砂糖中的铜不能 100%进入到测定液 中。为了评定由消化回收率引入的标准不确定度, 因此对该实验补做加标回收实验。实验表明,本法 铜的加标回收率为 96.2%~102.8%,样品回收率的 不确定度按 JJF1059-1999《测量不确定度评定与表 示》5.8 节计算:
urec2.1=(b++b-)2/2n
b+=(102.8-100)%=2.8%
b-=(100-96.2)%=3.8%
urec2.1=2.178%
取自由度为∞。
消化液中铜含量由原子吸收光谱仪。本次测定使用的原子吸收光谱仪是日本日立公司生产的Z2000 原子吸收光谱仪。
配制不同浓度的铜标准溶液,在规定条件下测定不同浓度溶液的吸光度值,如下表所示。
| 表 2 铜标准溶液吸光度值 |
由上表得出一元回归线性方程:c = 13.771x + 0.0026,r2=0.9998
式中: c——消化液中的铜含量 (μg/mL) ; x——样液的吸光度。
取置信概率为 95%,即 α=5%对线性回归方程进行 t 检验。 t = 141.4144, ta/2(n-2) = a/2 (4) = 2.7764,t>ta/2(n-2),说明该方程线形回归非常显著。
根据方程可以得到,该回归方程斜率 k = 13.771,截距 b = 0.0026,按贝塞尔公式计算出吸光度的标准偏差见(1)式。

然后,对斜率 k 和截距 b 的标准差进行分别估算(2) 、 (3)式。
自由度 v = n-2 = 4,取置信概率为 95%,k 和b 的扩展不确定度 U95(k)与 U95(b)分别为:
U95(k) = 0.1017 × t95(4) = 0.1017 × 2.78 = 0.283
U95(b)= 0.004465 × t95(4)= 0.004465 × 2.78 = 0.0124
其中,t95(4)= 2.78。


综上,可得出 k 和 b 的结果为(p = 0.95) :
k = 13.771±0.283,b = 0.0026±0.0124
最后,拟和回归直线引入的标准不确定度为:

U95(x)= 0.0002553×2.78 = 0.0007097 μg/mL
取某份白砂糖样品进行平行测定 10 次,测得 10 mL 糖液中的铜含量为 0.2014 μg/mL,由此得糖 液中铜的含量 (c) 引入的相对标准不确定度为 urec2.2 = 0.0007097/0.2014 = 0.003525, 其自由度为 6-2 = 4。
配制铜标准使用液是由国家钢铁材料测试中钢 铁研究总院提供的铜标准溶液(1000 μg/mL) ,已知 该标准溶液的不确定度为 0.3%,k = 2。
那么,在测定消化液中铜含量 c 时由铜标准溶液引入的相对标准不确定度为:
urec = 0.3%/2 = 0.0015
取自由度为∞。
铜标准使用液的配制方法如下:
用 1 mL 移液管吸取 1 mL1000 μg/mL 铜标准溶 液至 100 mL 容量瓶中,用 0.5%硝酸溶液定容至刻 度,得浓度为 10 μg/mL 标准使用液,再用 10 mL 刻度吸管吸取10 mL浓度为10 μg/mL标准使用液至 100 mL 容量瓶中,用 0.5%硝酸溶液定容至刻度, 得浓度为 1 μg/mL 标准使用液。
吸取 0.0、 2.5、 5.0、 10.0、 15.0、 20.0 mL 1 μg/mL 铜标准使用液,分别置入 25 mL 容量瓶中,用 0.5% 硝酸溶液稀释至刻度,混匀。容量瓶中每毫升分别 相当于 0.0、0.1、0.2、0.4、0.6、0.8 μg 铜。
由移液管引入的不确定度分量主要包括 2 个部 分:①移液体积:使用 1 mL A 级移液管,由国家 标物中心提供其允差为±0.001 mL,按均匀分布计 算,其标准不确定度为 0.001/31/2=0.0005774 mL; ② 校准温度与实验室温度不同产生的不确定度:仪器 的校准温度为 20℃,而实验室的温度为 20±10℃。 在 95%置信概率下,按正态分布计算,体积变化的 标准不确定度为 2.1×10-4×10×1/2 = 0.00105 mL。
合 成 以 上 两 项 标 准 不 确 定 度 为 (0.00057742+0.001052)1/2 = 0.001198 mL,其相对标 准不确定度为 0.001198/1 = 0.001198, 取其自由度为 ∞。
由容量瓶引入的不确定度分量主要包括 2 个部 分:①定容体积:使用 100 mLA 级容量瓶,由国家 标物中心提供其允差为±0.10 mL, 按均匀分布计算, 其标准不确定度为 0.10/31/2 = 0.05774 mL; ②校准温 度与实验室温度不同产生的不确定度:仪器的校准 温度为 20℃,而实验室的温度为 20 ±10℃。在 95% 置信概率下,按正态分布计算,体积变化的标准不 确定度为 2.1×10-4×10×100/2 = 0.105 mL。
合 成 以 上 两 项 标 准 不 确 定 度 为 (0.057742+0.1052)1/2= 0.1198 mL, 其相对标准不确定 度为 0.1198/100 = 0.001198,取其自由度为∞。
由刻度吸管引入的不确定度分量主要包括 2 个 部分:①移取体积:使用 10 mLA 级刻度吸管,由 国家标物中心提供其允差为 ±0.020 mL,按均匀分 布计算,其标准不确定度为 0.020/31/2=0.01155 mL; ②校准温度与实验室温度不同产生的不确定度:仪 器的校准温度为 20℃, 而实验室的温度为 20 ±10℃。 在 95%置信概率下,按正态分布计算,体积变化的 标准不确定度为 2.1×1014×10×10/2 = 0.0105 mL。
合 成 以 上 2 项 标 准 不 确 定 度 为 (0.011552+0.01052)1/2=0.01561mL,其相对标准不 确定度为 0.01561/10 = 0.001561,取其自由度为∞。
由容量瓶引入的不确定度分量主要包括 2 个部分:①定容体积:使用 100 mL A 级容量瓶,由国家 标物中心提供其允差为±0.10 mL, 按均匀分布计算, 其标准不确定度为 0.10/31/2=0.05774 mL;②校准温 度与实验室温度不同产生的不确定度:仪器的校准 温度为 20℃,而实验室的温度为 20±10℃。在 95% 置信概率下,按正态分布计算,体积变化的标准不 确定度为 2.1×10-4×10×100/2 = 0.105 mL。
合 成 以 上 2 项 标 准 不 确 定 度 为 (0.057742+0.1052)1/2=0.1198 mL,其相对标准不确 定度为 0.1198/100 = 0.001198,取其自由度为∞。
由容量瓶引入的不确定度分量主要包括 2 个部 分:①定容体积:使用 2 5mL A 级容量瓶,由国家 标物中心提供其允差为±0.03 mL, 按均匀分布计算, 其标准不确定度为 0.03/31/2 = 0.01732 mL; ②校准温 度与实验室温度不同产生的不确定度:仪器的校准 温度为 20℃,而实验室的温度为 20 ±10℃。在 95% 置信概率下,按正态分布计算,体积变化的标准不 确定度为 2.1×10-4×25/2=0.02625 mL。
合 成 以 上 2 项 标 准 不 确 定 度 为 (0.017322+0.026252)1/2 = 0.03145 mL,其相对标准 不确定度为 0.03145/25 = 0.001258,取其自由度为 ∞。
综上,由消化液中铜含量 c 引入的标准不确定 度的评定见下式。
取其自由度为 20。
由定容体积 V 引入的不确定度主要来源于定容 使用的 10 mL 容量瓶,属于 B 类评定分量。该不确 定度分量主要包括 2 个部分:①容量瓶体积:使用 A 级容量瓶,由国家标物中心提供其允差为±0.02 mL,按均匀分布计算,其标准不确定度为 0.02/31/2 =0.01155 mL; ②校准温度与实验室温度不同产生的 不确定度:仪器的校准温度为 20℃,而实验室的温 度为 20±10℃。在 95%置信概率下,按正态分布计 算,体积变化的标准不确定度为 2.1×10-4×10×10/2 = 0.0105 mL。
合成以上两项标准不确定度为
(0.011552+0.01052)1/2= 0.01561 mL, 其相对标准不确 定度为 0.01561/10 = 0.001561,取其自由度为∞。
本实验依照国标 GB/T 5009.1-2003《食品卫生 检验方法 理化部分 总则》 , 将白砂糖样品粉碎充分 混合均匀后随即取样,可认为样品是均匀的,代表 性充分,由此移入的不确定度可忽略不计。
白砂糖质量m引入的不确定度主要来自称量时 使用的天平自身存在的系统误差。本次实验使用的 电子天平为 FX-2000,查阅电子天平说明书,可得 知最大允差为 ±0.02 g,按均匀分布考虑,则有标准 不确定度为 0.02/31/2 = 0.01155 g。样品质量平均值 为 5.00 g,因此其相对标准不确定度为 0.01155/5.00 = 0.002310,取其自由度为∞。
将各个不确定度分量进行叠加,计算其合成标 准不确定度(下式) 。取其自由度为 32。图 2 为白 砂糖中铜含量的不确定度分量条形图。

|
图 2 白砂糖中铜含量的不确定度分量条形图 |
白砂糖样品中铜含量的最佳估计值为 0.96 mg/kg , 计 算 得 其 合 成 标 准 不 确 定 度 为 0.008678×0.96 = 0.008331 mg/kg。
当 veff =32,置信概率 p = 95%时,t 分布临界值 的包含因子 k95 = t95(32)= 2.04[3],可得扩展不确 定度:
U95 = 2.04×0.00331 = 0.01699 mg/kg。
原子吸收法测定白砂糖中铜含量的过程中,测 定结果的扩展不确定度为 0.01699 mg/kg,置信概率 p=95%,有效自由度 veff=32。veff样品铜含量是其真 实值可表示为 0.96 ±0.02 mg/kg。用传统方法计算其 相对误差为 2.08%, 在标准允许范围 (≤10%) 以内。
| [1] | 中国国家标准化管理委员会.GB/T 5009.13-2003 食品中铜的测定 [S]. 北京:中国标准出版社,2003. ( 2) 2)
|
| [2] | 国家质量技术监督局计量司.测量不确定度的评定与表示指南[M].北京:中国计量出版社,2000:30-166. ( 1) 1)
|
| [3] | 国家质量技术监督局.JJF1059-1999 测量不确定度评定与表示[M]. 北京:中国计量出版社,1999:8-10. ( 1) 1)
|
 2013
2013


