1993 年,由 ISO、IEC、BIPM、IFCC、IUPAC、 IUPAP、OIML 共 7 个国际组织共同组成国际测量不 确定度工作组起草制定了《测量不确定度表示指南》 (简称 GUM) 。为了促进 GUM 在我国的贯彻实施, 由全国法制计量委员会委托中国计量科学研究院起草 制定了国家计量技术规范 《测量不确定度评定与表示》 (JJF1059-1999)作为我国统一准则对测量结果及其 质量进行评定、表示和比较。
色值是白砂糖的一项重要的质量指标。中华人 民共和国国家标准《白砂糖》GB317—2006[1]中规定, 白砂糖色值测定使用方法为旋光法。本文通过对旋光 法测定白砂糖色值的测定过程进行分析,找出影响测 定结果不确定度的因素,通过建立数学模型对各个不 确定度分量进行计算,最终给出该法测定结果的合成 标准不确定度和扩展不确定度。
7230G 可见分光光度计(配套 10cm 比色皿) ; WAY-2S 数字阿贝折射仪;pH 计;滤膜过滤器。
0.1 mol/L 盐酸溶液;三乙醇胺-盐酸缓冲溶液。
称取白砂糖样品 100.0 g 于 200 mL 烧杯中,加 pH=7.0 的三乙醇胺-盐酸缓冲溶液 135 mL,搅拌至 完全溶解,倒入已预先铺好 0.45 µm 孔径微孔膜的 过滤器中,在真空下抽滤,弃去最初 50 mL 左右的 滤液,收集滤液应不少于 50 mL,用折射仪测定滤液的折光锤度,然后用比色皿装盛滤液,在分光光 度计上用 420 nm 波长测定其吸光度, 并用经过过滤 的三乙醇胺-盐酸缓冲溶液调零。
通过计算,即可算得该白砂糖样品的色值。
根据上述的实验步骤,计算白砂糖中二氧化硫
含量的数学模型为[2]:
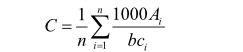
式中:C——色值(IU);
Ai——第 i 份样液在 420 nm 波长下测定所得的吸光度;
b——比色皿厚度(cm);
ci——第 i 份样液的固溶物浓度(g/mL)。 ( c = 折光锤度×相应视密度(20℃)/ 100)
测量不确定度是与测量结果相关联的参数,它 合理地赋予被测值的分散性。 该分散性主要涉及到 A 类不确定度、B 类不确定度和合成标准不确定度[2]: ①A 类不确定度:由测量列结果统计分布计算,用 实验标准偏差表征;②B 类不确定度:基于经验或 其他信息的概率分布估计出来,用标准偏差表征; ③合成标准不确定度:将 A 类不确定度、B 类不确 定度的平方和开方的方法叠加起来给出合成标准不 确定度。
该不确定度分量主要是由白砂糖样品的重复测 定所引入,属于不确定度的 A 类分量。
该不确定度分量主要是由分光光度计测定吸光 度的误差引入,属于不确定度的 B 类分量。
该不确定度分量主要是由比色皿的透色比误差 引入,属于不确定度的 B 类分量。
该不确定度分量主要是由折光锤度测定的误差 引入,属于不确定度的 B 类分量。
该不确定度分量主要是校准 pH 计时使用的二 级 pH 缓冲溶液引入,属于不确定度的 B 类分量。
对同一白糖样品重复测定 22 次, 测量值见表 1。
| 表 1 同一白砂糖样品 22 次重复测定值 |
由贝塞尔公式求得单次测量标准差 s(ci)为:
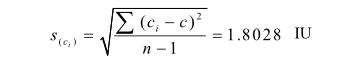
由测量重复性导致的标准不确定度 u(c)为:
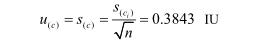
因此,重复测定的相对标准不确定度为 urel = 0.3843/126.7 = 0.003034,自由度为 νc = 22-1=21。
滤液的吸光度是由分光光度计测定得出,本次 测试使用的分光光度计为上海精密科学仪器有限公 司生产的 7230G 可见分光光度计。
该分光光度计透射比(即透射率)准确度为 ±0.8%。重复测定同一白砂糖样品得到其滤液在 420 nm 波长下的吸光度平均值为 0.312,经对数换算后 得,吸光度值为 0.312±0.004。
因此,其相对标准不确定度为 0.004/0.312 = 0.01282,取其自由度为 νA =∞。
同一配套比色皿透射比误差为±0.2%,按均匀 分布处理,则比色皿引入的标准不确定度为 ub = 0.002/31/2 = 0.001155 cm。 其相对标准不确定度为 0.001155/5= 0.000231, 取其自由度为 νb = ∞。
滤液浓度引入的标准不确定度主要是由折光锤 度测定的不确定度引入。
折光锤度是由阿贝折射仪测定得出,本次测试 使用的阿贝折射仪为上海精密科学仪器有限公司的 WAY-2S 数字阿贝折射仪。
该阿贝折射仪测量折射率准确度为±0.0002。 重 复测定同一白砂糖样品得到其滤液的折射率平均值 为 1.4042,锤度平均值为 42.2·BX,即该滤液的折 射率为 1.4042±0.0002。该温度下纯水的折射率为 1.3330, 通过计算, 得该滤液的锤度为 42.2±0.2·Bx。
查表计算得出滤液浓度的平均值为 0.5013 g/mL,计算得滤液浓度为 0.5013±0.0028 g/mL,因 此 , 其 相 对 标 准 不 确 定 度 为 0.0028/0.5013= 0.005585,取其自由度为 ν1= ∞。
校准 pH计时使用的二级 pH缓冲溶液也会对测 定结果的引入不确定度。从 pH 标准缓冲溶液的证 书可以查到,二级缓冲标准溶液的相对扩展不确定 度为 0.005(置信概率为 99.7%) ,其相对标准不确 定度为= 0.005/31/2 = 0.002887,自由度 ν3 = ∞。
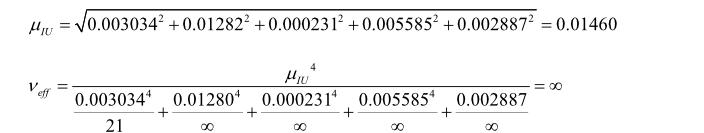
白砂糖样品中色值的最佳估计值为 126.7 IU, 计算得其合成标准不确定为 0.01460×126.7 = 1.8498 IU。
当 veff = ∞,置信概率 p=95%时,t 分布临界值 的包含因子 k95 = t95(∞)=1.96[3],可得扩展不确定 度:
U95=1.96×1.8498= 3.6256 IU。
旋光法测定白砂糖色值的过程中,测量结果的 标准不确定度为 1.8498 IU,在 95%的置信概率下, 取包含因子 k= 1.96,其扩展不确定度为 3.6256 IU, 白砂糖样品中色值真实值可表示为 126.7 ± 3.6 IU。 用传统方法计算其相对误差为 2.84%,在允许范围内。
| [1] | 中国轻工业联合会.GB 317-2006白砂糖[S]. 北京:中国标准出版社,2006. ( 1) 1)
|
| [2] | 国家质量技术监督局计量司.测量不确定度的评定与表示指南[M]. 北京:中国计量出版社,2000:30-166. ( 2) 2)
|
| [3] | 国家质量技术监督局.JJF1059-1999测量不确定度评定与表示[M]. 北京:中国计量出版社,1999:8-10. ( 1) 1)
|
 2011
2011

