文献标识码: A
2. 武汉大学雷电防护与接地技术教育部工程研究中心, 武汉 430072;
3. 湖南大学电气与信息工程学院, 长沙 410082
2. Engineering Research Center of Ministry of Education for Lightning Protection and Grounding Technology, Wuhan University, Wuhan 430072, China;
3. College of Electrical and Information Engineering, Hunan University, Changsha 410082, China
特高压输电线路是我国坚强智能电网的骨干网。作为我国电力传输的重要通道,特高压线路停运检修不仅会造成大量负荷损失,还会对大电网的稳定运行造成隐患。因此带电作业是特高压线路检修、消缺的重要手段,可以最大限度地保证供电可靠性,具有经济效益和社会效益[1]。
带电作业人员进入等电位时,与导线、杆塔共同形成组合空气间隙。组合空气间隙相较于原有的输变电工程长空气间隙发生了结构变化,其绝缘强度也发生了改变。
带电作业组合空气间隙是输电杆塔外绝缘设计的重要参考依据,学者们围绕该组合空气间隙开展了许多试验。胡毅等学者开展了特高压输电线路的组合间隙的真型试验,获取了试验数据[2-4]。试验发现在输电线路带电作业组合空气间隙中大约在距离导线0.4 m处存在最小放电电压位置,该放电电压值甚至低于相同长度下长间隙的放电电压值。因此,对组合间隙的研究是有必要的。然而,开展真型试验研究需要耗费人力物力,试验工作量巨大,难以考虑诸多影响因素对组合空气间隙放电特性的影响。
因此,后续的学者们通过简化工程间隙,使用棒电极、球电极和板电极等典型电极开展了组合空气间隙放电特性研究。研究涵盖了不同电极形状[5]、悬浮电极空间位置[6]、电压极性[7]、电压类型[8-9]、间隙结构[10]、海拔高度[11]等因素对简化组合间隙放电特性的影响。这为超特高压输变电工程的外绝缘设计提供更多依据。
后续学者们利用已有的放电特性试验数据开展了空气间隙放电模型研究,通过建立数学模型,预测类似间隙的放电电压特性,反映其绝缘强度。
然而已有的空气间隙放电模型的研究集中于长空气间隙。自从20世纪60年代开始,研究人员开展了不同间隙结构和不同尺寸的放电试验研究,获取了典型间隙的放电特性,初步建立了能够计算长空气间隙击穿电压的经验模型[12-15]。随后,研究人员进一步将间隙击穿电压等效为先导压降和流注压降之和,提出了半经验模型,其中最具代表性的有Mosch模型[16]和Rizk模型[17]。随着先进观测设备的应用,物理模型发展,不仅能够更准确地计算放电特性,而且能够描述放电发展过程[18-24]。
在组合空气间隙的放电模型研究领域,文献[25-26]分别建立了正极性操作冲击电压下组合空气间隙击穿电压的经验模型和半经验模型,在物理模型上的研究还较少。文献[27]研究了棒-悬浮棒-板这一组合空气间隙的放电电压特性,简要记录了该组合空气间隙的放电过程,为组合空气间隙放电物理模型研究提供了数据基础,文献[28]在其基础上,进一步分析并总结了悬浮棒位于不同位置时的放电物理过程,同样为组合空气间隙放电物理模型的研究提供了分析基础。
基于上述研究基础,文中首次建立了正极性操作冲击电压下组合空气间隙的放电物理模型。文中使用该模型计算了文献[27]中所研究的组合空气间隙击穿电压,并进一步计算得到了特征时刻。最后,将文中模型计算结果与试验测得的结果进行对比,验证了模型的有效性。在此基础上,通过进行消融试验进一步验证了模型参数选择是合理的;并使用文中模型对组合空气间隙击穿电压的影响因素进行分析。
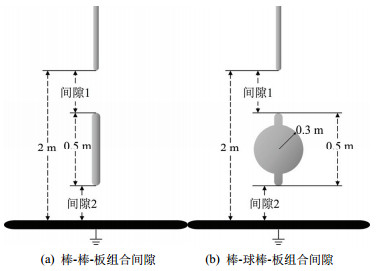
1 组合间隙放电仿真模型 1.1 放电物理过程分析文献[27]开展了间隙结构如图 1所示的棒-棒-板组合间隙和棒-球棒-板组合间隙的放电电压特性以及放电物理过程观测试验。文献[28]对上述组合间隙的放电物理过程进行分析。分析表明即使组合间隙中的悬浮导体位置发生变化,整个组合间隙的放电过程具有普遍规律:放电的起始总是从间隙1开始,间隙2的击穿总是不早于间隙1的击穿,组合间隙的放电发展过程是相似的。
|
图 1 间隙结构示意图 Fig. 1 Structure of the air gaps |
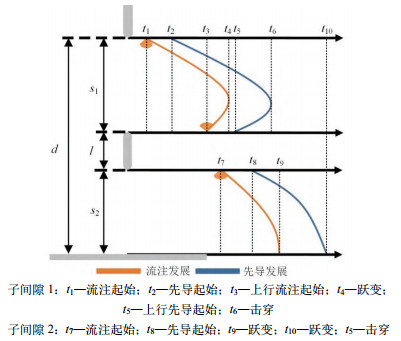
图 2展示了组合间隙放电发展过程。
组合间隙中间隙1和间隙2的放电过程是同时进行且相互影响的,其中间隙1放电过程主要包含了下行流注起始、下行先导起始、下行流注-先导体系发展、上行流注起始和发展、上行先导起始和发展以及间隙1击穿等过程。但是由于在文献[28]的放电过程观测结果中并未明显观测到上行先导起始和发展过程,且如图 2所示,上行先导起始和发展是后于间隙1跃变阶段的,因此在文中后续搭建的放电物理模型中不考虑间隙1的上行先导起始和发展过程。间隙2的放电过程主要由流注起始、先导起始、流注-先导体系发展以及间隙2击穿(组合间隙击穿)等过程组成。
基于上述组合间隙放电物理过程的分析总结,文中搭建了步进式组合空气间隙放电物理过程,计算流程图如图 3所示。

|
图 3 计算流程图 Fig. 3 Calculation flow chart |
其中,高压电极电位U2由外施电压u决定,文中研究的电压类型为标准正极性操作冲击电压,因此用双指数波来模拟,如式(1)所示。
| $ u(t) = \frac{{{U_{\rm{m}}}}}{{{{\text{e}}^{ - {{{t_{\rm{m}}}} \mathord{\left/ {\vphantom {{{t_{\rm{m}}}} {{t_1}}}} \right. } {{t_1}}}}} - {{\text{e}}^{^{ - {{{t_{\rm{m}}}} \mathord{\left/ {\vphantom {{{t_{\rm{m}}}} {{t_1}}}} \right. } {{t_1}}}}}}}} \cdot ({{\text{e}}^{ - {t \mathord{\left/ {\vphantom {t {{t_1}}}} \right. } {{t_1}}}}} - {{\text{e}}^{ - {t \mathord{\left/ {\vphantom {t {{t_1}}}} \right. } {{t_1}}}}}) $ | (1) |
式中:Um为电压峰值;tm为电压峰值时间;t1、t2为时间常数,由波前时间Tf和视在半峰值时间Tt求得:
| $ \left\{ \begin{array}{l} {t_1} = \frac{{{T_{\rm{t}}}}}{{\ln 2}} \hfill \\ {t_2} = \frac{{0.6{T_{\rm{f}}}}}{{\ln 7}} \hfill \end{array} \right. $ | (2) |
在计算悬浮电极电位U2时,如果间隙1还未击穿,则认为悬浮电极电位为感应电位,通过有限元仿真软件可直接求得;如果间隙1已经击穿了,则间隙1为先导通道,此时悬浮电极电位通过式(3)、(4)求得[33]。
| $ \Delta {U_1} = \frac{{50{l_1}}}{{1 + {{3.89} \mathord{\left/ {\vphantom {{3.89} {{l_1}}}} \right. } {{l_1}}}}} + 37.5\ln (8 - 7{{\text{e}}^{ - \frac{{1.33{l_1}}}{{1 + {{3.89} \mathord{\left/ {\vphantom {{3.89} {{l_1}}}} \right. } {{l_1}}}}}}}) $ | (3) |
| $ {U_2}(t) = u(t) - \Delta {U_1} $ | (4) |
流注起始是长空气间隙放电由电离阶段转向放电发展阶段的转折点,也是组合空气间隙放电中由电离阶段转向放电发展阶段的转折点。文中采用基于临界电荷法的流注起始判据[18]。其数学表达式如下:
| $ N = \exp (\int\limits_0^l {(\alpha - \eta ){\text{d}}z} ) \geqslant {N_{{\rm{stab}}}} $ | (5) |
式中:l为电离层边界,由α=η确定,α为电离系数,η为附着系数,均为关于电场的函数;Nstab为临界电荷数,该参数的取值需随间距变化进行修正,文中中Nstab取值为1×108[36]。
| $ \alpha = \left\{ {\begin{array}{*{20}{l}} {2 \times {{10}^{ - 16}}{{\text{e}}^{(\frac{{ - 7.248 \times {{10}^{ - 15}}}}{{E/N}})}}N, }&{\frac{E}{N} > 1.5 \times {{10}^{ - 15}}} \\ {6.619 \times {{10}^{ - 17}}{{\text{e}}^{(\frac{{ - 5.593 \times {{10}^{ - 15}}}}{{E/N}})}}N, }&{\frac{E}{N} < 1.5 \times {{10}^{ - 15}}} \end{array}} \right. $ | (6) |
| $ \eta = P(0.012\;983 - 5.4 \times {10^{ - 4}}\frac{E}{P} + 8.7 \times {10^{ - 6}}{(\frac{E}{P})^2}) $ | (7) |
式中:E为间隙轴线电场;P为大气压力,标准大气压下取值为0.1 MPa;N为空气中粒子数密度,大气压下取值大致为2.45×1019 cm–1;E/N、E/P均为约化电场。
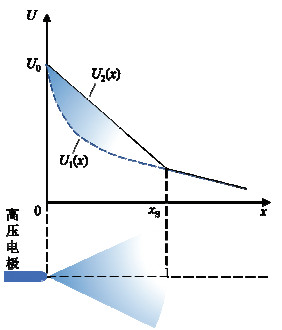
1.2.2 流注发展模型正极性流注起始后,随着施加电压进一步提升,流注继续向前发展。流注稳定发展时的最低电场为流注稳定电场Est。研究表明在流注发展过程中,流注区域电位梯度Es等于稳定电场Est,取值为400~500 kV/m[20]。根据这一原理,Gallimberti、Bondiou[21]等学者提出了流注发展模型,利用背景电势的空间分布和流注区域电位梯度Es即可计算流注区域的长度,如图 4所示。流注区域轴向长度xs可由下式计算得到:
| $ U({x_{\rm{s}}}) = U(0) - {E_{\rm{s}}}{x_{\rm{s}}} $ | (8) |
|
图 4 流注区域发展与流注长度计算示意图 Fig. 4 Schematic diagram of streamer region development and streamer length calculation |
式中:U1(x)为间隙轴线的背景电势空间分布。流注发展过程中,流注区域内的正极性空间电荷会将轴线上背景电势U1(x)抬升至U2(x),抬升后局部电位的斜率即为流注区域的平均场强Es。
与正极性流注发展相似,随着悬浮导体表面电场增强,负极性上行流注会从悬浮导体向高压电极方向发展,其轴向长度也可以通过空间电位分布与负极性流注电位梯度Esn(约为750 kV/m)[29]确定。
1.2.3 流注空间电荷计算模型确定了流注区域长度后,还需计算流注区域的空间电荷量。文中采用Goelian等人提出的空间电荷计算模型[23]:
| $ Q = 4K{{\rm{ \mathsf{ π} }}}{\varepsilon _0}\int_0^{{x_{\text{s}}}} {({U_2}(x) - } {U_1}(x)){\text{d}}x $ | (9) |
式中:Q为空间电荷量;K为几何常数,取值为0.3~0.35,文中取K为0.35[23];ε0为真空介电常数,为8.854×10–12 F/m。
1.2.4 先导起始模型先导放电是含悬浮导体长空气间隙放电的第2个阶段。先导起始是间隙从流注放电转向先导-流注体系发展的标志。Gallimberti根据长空气间隙放电观测结果认为当流注茎温度上升至负离子脱附的临界温度(约为1 500 K)时,流注茎中的负离子会转化为自由电子和中性分子,此时流注茎通道的电导率快速提升,流注茎转化为先导[20]。
Bondiou和Gallimberti根据上述原理,建立了流注茎内能热平衡方程组并利用该热平衡方程组,分析负离子脱附的临界温度所对应的流注空间临界电荷量[21],Gallimberti提出了先导起始的1 μC临界电荷判据,即,当流注区域空间电荷量达到1 μC时,先导起始。
1.2.5 先导流注体系发展模型先导-流注体系发展过程中,流注区域头部电离区产生的电子进入先导-流注体系中,在流注根部移动过程中再次发生弹性碰撞和非弹性碰撞,使转化区温度上升,在温度达到临界温度后,形成了新的先导段。先导通道电导率较高,内部电场较小,先导通道的增长也促使流注区域头部电场增强,进一步促进流注区域头部电离。
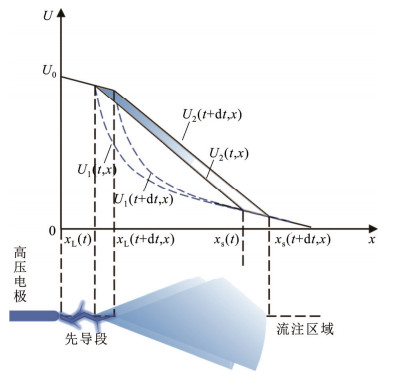
先导-流注体系发展计算中,先导-流注体系空间电荷计算是放电物理模型计算的关键。图 5是先导-流注体系发展的示意图,时刻t时,在外施电压U0(t)的影响下,间隙轴线空间电位分布(背景电势)为U1(t, x)。考虑先导通道中的正极性空间电荷和先导通道的压降,先导头部的电位为UL(t),流注区域的背景电势为
|
图 5 先导流注体系空间电荷示意图 Fig. 5 Schematic diagram of space charge of leader-streamer system |
流注区域范围的确定以及流注区域空间电荷的计算可使用式(10)进行计算。
| $ \begin{array}{l} Q = 4K{{\rm{ \mathsf{ π} }}}{\varepsilon _0}\int_{{x_{\text{L}}}(t)}^{{x_{\text{s}}}(t + {\text{d}}t)} {(({U_2}(t + {\text{d}}t, x) - } {U_1}(t + {\text{d}}t, x)) - \\ \;\ \ \ \ ({U_2}(t, x) - {U_1}(t, x))){\text{d}}x \end{array} $ | (10) |
与流注发展阶段不同的是,流注区域末端电位不再为高压电极上的施加电压,而是先导头部电位,而且流注区域也不再是从高压电极向前发展,而是从先导头部延伸,因此有必要确定先导头部的电位和位置。文中采用Lalande等学者提出的先导发展模型计算先导通道的增长,该模型基于Gallimberti的假设[20],认为先导段为一被包裹的均匀圆柱体,其内部压力、温度和粒子密度是恒定的。在Gallimberti模型的基础上,Lalande[23]等学者使用流注区域产生的新增空间电荷表征先导通道内部热力学特性,计算式为:
| $ {a_i}^2(t + {\text{d}}t) = {a_i}^2(t) + \frac{{(\gamma - 1){E_{{\rm{L}}i}}(t)\Delta {Q_{\rm{s}}}}}{{{{\rm{ \mathsf{ π} }}}\gamma {p_0}}} $ | (11) |
| $ {E_{{\rm{L}}i}}(t + {\text{d}}t) = {E_{{\rm{L}}i}}(t) \cdot \frac{{{a_i}^2(t)}}{{{a_i}^2(t + {\text{d}}t)}} $ | (12) |
式中:ai为第i段先导段的半径;γ为定压比热容和定容比热容的比值,取1.4[30];ELi为第i段先导段的内部电场;ΔQs为新增空间电荷量;p0为气压。
对于由流注茎转化成的初始先导段,假设其半径为0.001 m,内部电场为400 kV/m,长度为0.02 m[31]。
在确定每一段先导段的内部电场后,即可计算t时刻整个先导通道的电压降ΔUL,计算式为:
| $ \Delta {U_{\rm{L}}}(t) = \sum\limits_{i = 1}^k {{E_{{\rm{L}}i}}(t) \cdot } \Delta {x_{{\rm{L}}i}} $ | (13) |
式中:k为先导段的数量;ΔxLi为先导段间隙轴线分量的长度。
因此,根据高压电极上的施加电压,即可确定先导头部电压UL(t),计算式为:
| $ {U_{\rm{L}}}(t) = {U_0}(t) - \Delta {U_{\rm{L}}}(t) $ | (14) |
根据电荷守恒原理,流注区域头部电离区产生的进入先导-流注体系的电子与残留的空间电荷量相等,因此计算新增先导段的长度如下:
| $ \Delta {X_{{\rm{L}}i}} = {{\Delta {Q_{\rm{s}}}} \mathord{\left/ {\vphantom {{\Delta {Q_{\rm{s}}}} {{q_{\rm{L}}}}}} \right. } {{q_{\rm{L}}}}} $ | (15) |
式中:ΔXLi为新增先导段的长度;qL为单位长度先导通道的电荷量,取50 μC/m[32]。
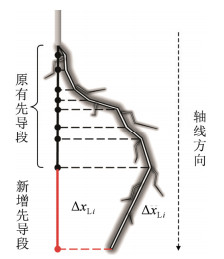
如图 6所示,先导通道的发展具有明显的随机性,先导段长度ΔXLi与先导段间隙轴线分量的长度ΔxLi具有如下关系:
| $ \Delta {x_{{\rm{L}}i}} = \Delta {X_{{\rm{L}}i}}\cos \varphi $ | (16) |
|
图 6 先导通道发展路径随机性示意图 Fig. 6 Schematic diagram of randomness of development path of leader channel |
式中:φ为先导段与间隙轴线间的夹角,角度范围取0~90°。根据长空气间隙放电试验数据,确定了φ的分布,其概率密度函数[32]如下:
| $ f(\varphi ) = {a_1}{{\text{e}}^{ - {{({{(\varphi - {b_1})} \mathord{\left/ {\vphantom {{(\varphi - {b_1})} {{c_1}}}} \right. } {{c_1}}})}^2}}} $ | (17) |
式中:a1、b1、c1通过试验数据拟合得到,在高压电极为棒型电极的间隙中,a1=3.67,b1=0.052,c1=0.289 3。通过生成符合该概率密度函数的随机数,即可确定新增先导段间隙轴线分量的长度ΔxLi。
2 模型验证根据文献[27]的试验参数,文中在COMSOL Multiphysics有限元仿真软件上搭建了1:1模型,采用静电场仿真计算了轴线的电场和电压分布,得到各组合间隙的轴线电场和电压分布。模型图、轴线电压分布图、轴线电场分布图(见附录A)。
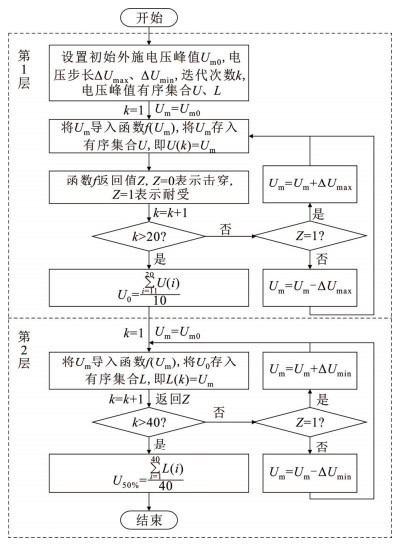
2.1 升降法计算流程利用如图 3所示的计算流程,可以计算出在操作冲击电压峰值Um为单个固定值下该组合间隙是否击穿或者耐受。为了计算出组合间隙在正极性操作冲击电压下的50%击穿电压,文中将图 3所示计算流程封装成函数f(Um),并按照标准[34]中操作冲击电压下的U50计算方法-升降法调用函数f(Um),最后计算得到每个组合间隙在正极性操作冲击电压下的50%击穿电压,计算流程图如图 7所示。
|
图 7 U50升降法计算流程图 Fig. 7 Calculation flow of the U50 by up-and-down-methods |
在文中计算过程中取ΔUmax为50 kV,ΔUmin为0.03U0。
此外,使用文中提出的物理模型仿真计算确定了组合间隙的击穿电压后,采用如图 3所示的计算流程还可以对各组合间隙的具体放电发展过程进行仿真计算。
2.2 模型参数对50%击穿电压的敏感性分析1.2节中介绍了文中的放电物理模型,主要包含流注起始模型,流注发展模型,流注空间电荷计算模型,先导起始模型和先导流注体系发展模型等。过去研究学者们围绕上述模型都开展了不同的研究,对于其中一些重要参数的取值仍较模糊,因此文中针对其中一些重要参数的取值开展了参数消融试验,主要试验参数有:流注起始模型中的临界电荷数Nstab、流注发展模型中的流注稳定电场Est、流注空间电荷计算模型中的几何常数K、先导起始模型中的临界电荷判据Q0以及先导发展体系发展模型中的单位长度先导通道电荷量qL。由于使用放电物理模型计算棒-棒-板组合间隙和棒-球棒-板组合间隙的放电电压值和放电特征参数值时差异较小,因此消融试验仅针对棒-棒-板组合间隙。
引入单个间隙结构的误差(single error, SE)
| $ {\varepsilon _{{{\rm{S}}}{{{\rm{E}}}_i}}} = \frac{{{U_{i.{\rm{test}}}} - {U_{i.{\rm{cal}}}}}}{{{U_{i.{\rm{test}}}}}} $ | (18) |
式中:Ui.test为第i个工况下试验测得的击穿电压值;Ui.cal为第i个工况下模型计算得到的击穿电压值;εSEi为第i个间隙结构的误差,i取1时对应间隙1长度0.1 m,i取9时对应间隙1长度1.2 m,其余情况与文中组合间隙的9个工况对应。
2.2.1 临界电荷数敏感性分析文献[24]指出计算流注起始电压时采用临界电荷判据的临界电荷数Nstab应取0.55×108;而文献[36]中指出临界电荷数应取1×108。因此本节内容主要对比临界电荷数在不同取值时模型的计算精度。
当Nstab值取1×108时,模型整体的误差指标MAE更小,MCE指标与Nstab取值为0.55×108时一致,因此,Nstab值取1×108是更合理的。整体表现上临界电荷数Nstab这一参数取值对击穿电压的影响较小。
2.2.2 流注稳定电场值敏感性分析文献[20]指出在流注发展阶段,流注稳定电场Est这一参数取值范围是400~500 kV/m。因此该节主要对比该参数不同取值时模型的计算精度。
对于间隙1的流注稳定场强Est1,其取值从450 kV/m逐渐增大至800 kV/m的过程中,MAE逐渐减小,在700~750 kV/m时取得最小值,然后逐渐增大;类似地,最大计算误差指标MCE在取值为700 kV/m时最小。因此认为间隙1的流注稳定场强Est1取值为700 kV/m时是最优的。对于间隙2的流注稳定场强Est2,取值为400 kV/m或500 kV/m时误差均大于取值为450 kV/m时,因此在该模型中,认为间隙2的流注稳定场强Est1取值为450 kV/m时是最优的.
但是间隙1的Est1取值超过了过去国外试验中测量得到的该值的范围400~500 kV/m。对该结果进行分析如下。
过去,研究人员通过测量发现一些间隙结构下的流注电场值超过了500 kV/m。文献[38]利用测量了球-板间隙的流注空间电场值,发现当只有一次流注起始时,流注空间电场大约为500 kV/m,但是当发生第2次流注起始时,流注空间电场值上升到了接近600 kV/m。过去国外实验中得到的400~500 kV/m这一流注稳定电场范围主要是从极不均匀电场空气间隙放电试验中得到的,而文献[38]中的球板间隙结构的均匀度更高,使得不稳定流注发生的概率增大,流注空间电荷积累更多,流注空间电场值提高。文中研究的棒-棒-板组合间隙和棒-球棒-板组合间隙,观测结果表明同样存在二次流注起始现象[28],这使得流注空间电场提高了。此外,间隙1中阳极是高压电极,阴极是悬浮电极,间隙1的正流注在发展过程中无法像阴极接地时快速泄放掉,导致空间电荷积累更多,流注空间电场值进一步升高。由于流注稳定电场值反映的是流注在间隙内发展过程中的均值,这表明在组合空气间隙中,二次流注起始现象以及悬浮电极的存在共同导致了流注稳定电场值这一参数取值大于一般取值,甚至达到700 kV/m。
2.2.3 几何常数敏感性分析文献[23]中指出几何常数K取值范围是0.3~0.5。该节对比该参数对计算精度的影响。
随着K值逐渐增大,误差指标MAE逐渐下降,K值取0.35时最小,MCE指标保持不变,因此认为K值取0.35时MAE最优。整体上,参数K对于击穿电压的影响较小。
2.2.4 临界电荷判据敏感性分析文献[21]指出电晕区积累空间电荷量大于1 μC时,先导起始;但文献[37]认为不同的几何条件下,积累电荷量不需要到达1 μC就可以发生先导起始,最小在大约0.2 μC时就可以产生先导起始。因此本节对比该参数对模型计算精度的影响。
随着临界电荷判据Q0取值逐渐增大,指标MAE逐渐减小,指标MCE不变。因此,认为Q0取值为1 μC时为最优。
2.2.5 单位长度先导通道电荷量敏感性分析文献[32]指出单位长度先导通道电荷量qL的取值范围为40~65 μC/m。因此本节对比该参数不同取值时模型的计算精度。参数qL取值为50 μC/m时,指标MAE最小;qL变化过程中MCE保持不变。因此,qL取值为50 μC/m为最优。
2.3 模型参数对放电电压时刻的敏感性分析与2.2节类似,本节计算不同模型参数下放电特征时刻的计算结果。结果见附录表B6—B7。
由附表B6—B7数据分析:临界电荷数Nstab对放电特征时刻影响较小,可以忽略不计。
流注稳定电场影响间隙的流注发展速度,在间隙1长度为0.3 m时,随着Est1增大,流注起始发展到先导起始的时间增加。K值同样影响流注发展速度,当K值取0.35时,其流注发展的时间相较于取0.3时更短。
参数Q0影响先导起始的难度,Q0取值越小,先导起始难度越小。数据表明Q0随着间隙结构的变化而变化,其物理含义是先导起始所需积累的空间电荷量。间隙1由高压棒电极和悬浮棒电极组成,棒棒间隙的不均匀程度相较于棒板间隙的不均匀程度较小,且悬浮棒电极感应的正电荷使得电场更均匀。当悬浮棒电极靠近高压棒电极时,悬浮棒电极感应电荷量增大,电场更加均匀,空间电荷更容易积累,先导更容易起始。因此间隙1长度较小时,Q0取值为0.2 μC时间隙1先导起始时刻更接近试验值。参数qL的取值对放电特征时刻的影响较小。
综上所述,文中选择了使得整体误差较小的固定参数值,如表 1所示。
|
|
表 1 模型参数设置表 Table 1 Parameters of the model |
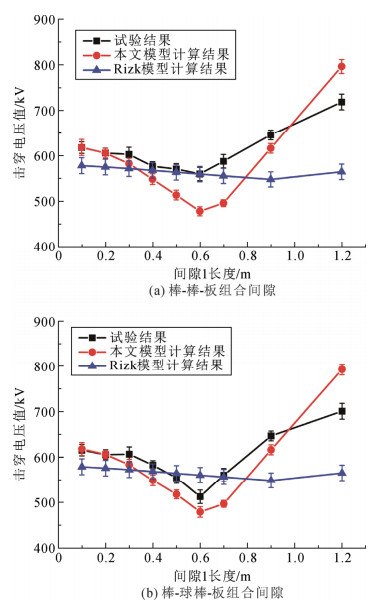
文献[27]中试验得到的棒-棒-板组合间隙和棒-球棒-板组合间隙的击穿电压值均已经过大气校正到了标准大气压下。按照图 7所示流程对击穿电压值进行计算,并将计算结果与试验结果以及Rizk模型[35]计算结果进行对比,如图 8所示。
|
图 8 仿真计算结果对比图 Fig. 8 Comparison of simulation results |
文中采用平均绝对误差(mean absolute error, MAE)εMAE和最大计算误差(max calculation error, MCE)εMCE两个指标评价模型精度。计算式如下:
| $ {\varepsilon _{{{\rm{MAE}}}}} = \frac{1}{n}\sum\limits_{i = 1}^n {\frac{{\left| {{U_{i.{\rm{test}}}} - {U_{i.{\rm{cal}}}}} \right|}}{{{U_{i.{\rm{test}}}}}}} $ | (19) |
| $ {\varepsilon _{{{\rm{MCE}}}}} = \mathop {\max }\limits_{i \in \{ 1, 2, \cdots , n\} } \left\{ {\frac{{\left| {{U_{i.{\rm{test}}}} - {U_{i.{\rm{cal}}}}} \right|}}{{{U_{i.{\rm{test}}}}}}} \right\} $ | (20) |
式中:Ui.test为第i个工况下试验测得的击穿电压值;Ui.cal为第i个工况下模型计算得到的击穿电压值;n为工况的数量,文中对于棒-棒-板组合间隙和棒-球棒-板组合间隙分别研究了9个工况,因此n=9。
根据图 8的计算结果以及式(19)—(20)计算模型精度,分析结果如下所述。
棒-棒-板组合间隙中,Rizk模型计算得到击穿电压的MAE为6.91%,MCE为21.45%;文中物理模型计算得到击穿电压的MAE为7.10%,MCE为15.58%。Rizk模型计算得到的最小击穿电压位置为0.7~1.2 m,与试验结果不同;文中模型计算得到的最小击穿电压位置和试验得到的最小击穿电压位置一致,均为0.5~0.7 m。
棒-球棒-板组合间隙中,Rizk模型计算得到击穿电压的MAE为5.75%,MCE为19.35%;文中物理模型计算得到击穿电压的MAE为5.83%,MCE为13.10%。Rizk模型计算得到的最小击穿电压位置为0.7~1.2 m,与试验结果不同;文中模型计算得到的最小击穿电压位置和试验得到的最小击穿电压位置一致,均为0.5~0.7 m。
2.4.2 讨论对比使用不同模型计算击穿电压的结果,发现在MAE指标上,Rizk模型和文中提出的放电物理模型的差异不大,但是文中模型在最大误差指标上的表现优于Rizk模型,且文中模型更准确地计算出组合间隙的最小放电位置,相较于Rizk模型更能反映组合间隙的放电特性。
此外,由图 8可以看出,Rizk模型的计算结果更趋近于一条横线,使用Rizk模型时,间隙1长度的变化对击穿电压值的影响很小,即悬浮电极对于组合空气间隙的影响较小。这一结论显然与试验结果不符,从图形趋势分析,本文模型的计算结果与试验结果更加匹配。
对比不同组合间隙击穿电压值计算结果,由附图B2—B3可知,棒-棒-板组合间隙和棒-球棒-板组合间隙的轴线电场和电压曲线差异很小,且轴线电场和电压值是文中物理模型的主要输入变量,这是使得文中仿真计算得到的两个组合间隙的结果差异很小的主要原因。但从文献[27]的试验对比结果可知,两种组合间隙的击穿电压值存在一定差异,当间隙1长度为0.5~0.7 m时,棒-球棒-板组合间隙的放电电压值显著小于棒-棒-板组合间隙的放电电压值,这使得文中模型计算结果与试验结果差异较大。上述差异在间隙1长度为0.6 m时尤其显著。
对上述现象进行分析推论如下:文献[39]中提出电极表面流注茎的数量并不总是1随着电极曲率半径增大,流注茎数量平均值增大。结合文中对流注稳定电场值这一参数的影响因素试验的分析结论推测间隙的不均匀度会影响流注茎数量,进而影响流注稳定电场值,且不均匀度与流注稳定电场值呈现出负相关特性。
对于棒-棒-板组合间隙,随着间隙1长度增加,间隙1不均匀度增大,间隙2不均匀度减小。因此间隙1流注稳定电场值应该减小,间隙2流注稳定电场值应该上升。文中选择的流注稳定电场值这一参数基于考虑所有间隙工况的误差最小值确定的,并未针对每一间隙工况单独赋值,结合附录表B2数据可知,当间隙2流注稳定电场值为500 kV/m时,间隙1长度为0.5~0.7 m的放电电压误差减小。
对于棒-球棒-板组合间隙,随着球棒电极的移动,间隙1和间隙2不均匀程度的变化特性与棒-棒-板电极几乎相同。但是由于试验所用球棒电极为空心球电极和实心棒电极焊接而成。相较于实心棒电极,在外施电压和间隙1流注的空间电荷电场影响下,球棒电极的空心球上表面会感应更多负电荷,下表面感应更多正电荷。空心球电极表面感应的更多的负电荷将产生更大的电场,这会增大球棒端部的电离过程,促进间隙1上行流注的起始和发展、以及间隙2的下行流注起始和发展过程,使得棒-球棒-板组合间隙的放电电压值小于棒-棒-板组合间隙的放电电压值。且当间隙1长度较小时,间隙1上行流注对放电影响较小;当间隙1长度较大时,间隙2放电过程对整个组合间隙的放电影响也较小;悬浮电极位于最小放电电压位置附近时,空心球棒表面感应的电荷既促进间隙1上行流注起始与发展,又促进间隙2的下行流注起始与发展,使得棒-球棒-板组合间隙在最小击穿位置的放电过程更容易发展,放电电压值小于相同位置下的棒-棒-板组合间隙。
综上所述,后续研究应该进一步关注间隙结构不均匀程度对流注稳定电场的影响以及悬浮电极感应电荷的分布情况对放电发展的影响。
2.5 放电特征时刻计算结果验证与讨论对比文中模型计算得到的放电特征参数与文献[27]中试验得到的放电特征时刻(见表 2、3),分析如下所述。
|
|
表 2 棒-棒-板组合间隙放电特征时刻对比 Table 2 Comparison of discharge characteristic time of rod-rod-plane combined air gaps |
|
|
表 3 棒-球棒-板组合间隙放电特征时刻对比 Table 3 Comparison of discharge characteristic time of rod-spere+rod-plane combined air gaps |
比较试验与仿真计算的放电特征时刻:当间隙1长度较小时,仿真计算的放电特征时刻与试验观测到的较接近;当间隙1长度较大时,仿真计算的放电特征参数与试验观测的相差较大,主要体现在间隙2流注起始时刻和间隙击穿时刻。
3 讨论 3.1 模型泛化试验文中所提物理模型是基于文献[28]中观测到的2 m间隙长度的组合间隙放电物理过程搭建的,第2章中仅验证了本模型在文献[27-28]中的2 m组合空气间隙绝缘性能预测上的准确性,无法验证该模型的泛化性能。为了验证本模型在预测组合空气间隙放电电压上的泛化能力,对文献[11]中试验得到的2.5 m组合空气间隙及3 m组合空气间隙的放电电压进行计算,计算结果见图 9。

|
图 9 模型泛化能力验证 Fig. 9 Verification of generalization ability of the model |
按照式(19)—(20)计算本模型的计算精度,得到2.5 m组合间隙击穿电压的MAE为4.52%,MCE为9.08%;3 m组合间隙击穿电压的MAE为7.03%,MCE为11.16%。误差均小于12%。
上述结果表明了文中所提物理模型具有良好的泛化能力,能够适应不同的间隙尺度。
带电作业组合间隙通常是由塔身(横担)、作业人员以及导线构成的。文中研究的棒-棒-板组合间隙中高压棒电极可以模拟导线中的凸起,悬浮棒电极模拟作业人员屏蔽服上的凸起或手指,板电极模拟塔身或横担;类似地,棒-球棒-板组合间隙中地悬浮球棒电极也可以模拟身着屏蔽服的作业人员及凸起。因此本模型能够适用于预测带电作业组合间隙中的导线-作业人员-塔身(横担)组合间隙。此外,GB 26859[40]中指出110~330 kV电压等级输电线路等电位带电作业中的最小组合间隙距离分别是1.2、2.1和3.1 m。因此基于已有验证成果,本模型适用于110~330 kV电压等级的输电线路等电位作业组合间隙绝缘性能预测。
3.2 影响因素对照试验利用文中模型对棒-棒-板组合间隙和棒-球棒-板组合间隙击穿电压的影响因素展开计算分析,影响因素包括悬浮电极长度和悬浮电极形状等。
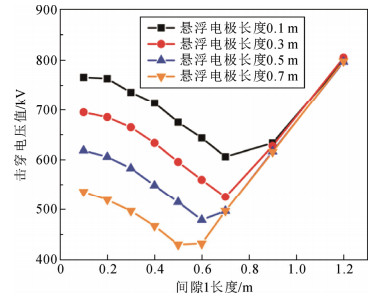
3.2.1 总间隙长度一定时悬浮电极长度影响分析首先开展了在棒-棒-板组合空气间隙中,总间隙长度一定时,悬浮电极长度变化对组合空气间隙击穿电压的影响的对照试验。其中,总间隙长度指高压电极端部到地电极的最短距离,文中取2 m。试验结果如图 10所示。
|
图 10 悬浮电极长度变化对击穿电压的影响结果(总间隙长度不变) Fig. 10 Result of variation in floating electrode length (total gap length remains unchanged) |
从图 10结果可知,当间隙1长度较小时,悬浮电极长度越小,击穿电压值越大,当间隙1长度较大时,悬浮电极长度变化基本不影响组合空气间隙的击穿电压值。这是由于当间隙1长度较小时,组合空气间隙的击穿电压值主要由间隙2长度决定,因此在总间隙长度一定的情况下,悬浮电极长度减小,间隙2长度就增大,组合空气间隙的击穿电压值相应增大。
此外还发现在总间隙长度一定时,最小放电位置随着悬浮电极长度增大,明显呈现出向高压电极靠近的趋势。
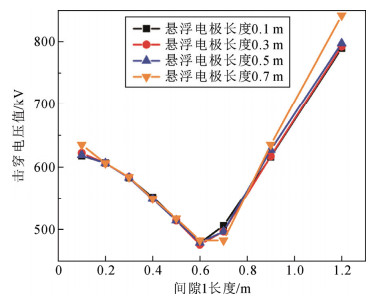
3.2.2 组合间隙长度一定时悬浮电极长度影响分析本章开展了棒-棒-板组合间隙长度一定时,悬浮电极长度变化对组合空气间隙击穿电压影响的对照试验。其中,组合间隙长度指的是在高压电极端部到地电极的最短距离中纯空气间隙的长度,文中取1.5 m。实验结果如图 11所示。
|
图 11 悬浮电极长度变化对击穿电压的影响结果(组合间隙长度不变) Fig. 11 Result of variation in floating electrode length (combined gap length remains unchanged) |
由图 11可知,当组合间隙长度一定时,悬浮电极长度对组合空气间隙击穿电压的影响较小。间隙1长度分别为0.1、0.7和1.2 m时悬浮电极长度对击穿电压影响稍大。当间隙1长度为0.1 m和1.2 m时,悬浮电极长度越长,组合间隙击穿电压越高;当间隙1长度为0.7 m时,悬浮电极长度越长,组合间隙击穿电压越低;悬浮电极长度增加,最小击穿电压位置几乎保持不变。
上述结果表明,悬浮电极的尺寸不是组合空气间隙击穿电压的主要影响因素。
3.2.3 悬浮电极形状影响分析本节开展了棒-球棒-板组合空气间隙中悬浮电极球棒的球径变化对组合空气间隙击穿电压影响试验,其中悬浮电极球半径0 m对应棒-棒-板组合间隙,悬浮电极球半径0.15 m对应图 1(b)中的棒-球棒-板组合间隙。
从图中看出,悬浮电极球半径对于组合空气间隙击穿电压的影响可以忽略不计。
4 结论1)针对模型中参数取值问题,文中首先开展了模型参数的敏感性分析试验,结果表明在文中所提模型中,流注稳定电场值是影响组合空气间隙击穿电压的主要因素;流注稳定电场值、形状参数和先导起始判据等参数随着间隙结构的变化其最优取值也会发生变化。
2)确立了模型最优参数后,基于文中建立的放电物理模型对棒-棒-板组合间隙和棒-球棒-板组合间隙的击穿电压值和放电特征时刻值进行计算。发现对于击穿电压值,棒-棒-板组合间隙中平均计算误差为7.10%,最大计算误差为15.58%,棒-球棒-板组合间隙中平均计算误差为5.83%,最大计算误差为13.10%,且能够准确计算组合间隙的最小放电位置,文中模型表现优于Rizk模型;而对于放电特征时刻值,两个组合间隙都是的计算结果都较为相符。
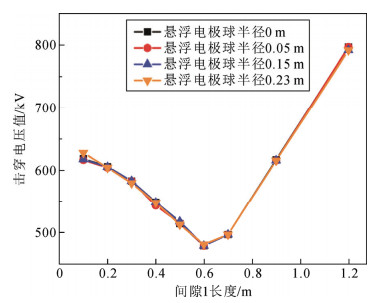
|
图 12 悬浮电极形状变化对击穿电压的影响结果 Fig. 12 Result of variation in floating electrode shape (combined gap length remains unchanged) |
3)进一步地,文中还开展了泛化能力验证试验和影响因素对照试验。泛化试验结果表明在文中所提模型能够准确地拓展到2.5 m和3 m组合空气间隙击穿电压预测中,平均计算误差分别是4.52%和7.03%,最大计算误差均不超过12%;此外对照试验结果表明悬浮电极长度和悬浮电极形状对组合空气间隙击穿电压的影响较小,组合空气间隙长度是击穿电压的主要影响因素。
4)总的来说,文中模型的计算值与试验值对比结果表明,文中提出的组合间隙放电物理模型能够仿真出组合间隙的放电特性,放电特征参数的计算结果与试验结果也较为相符,基于已有验证结果,本模型适用于110~330 kV电压等级的输电线路等电位作业中组合间隙绝缘性能的预测。但是本模型存在对实际工程间隙的简化过程,在未来的工作中,将开展针对实际工程间隙的绝缘性能的预测工作,提高预测精度。
附录见本刊网络版(http://hve.epri.sgcc.com.cn)。
附录A 附图
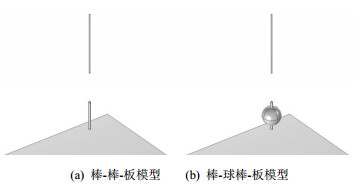
|
图 A1 模型图 Fig. A1 Model diagram |
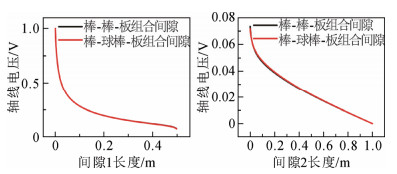
|
图 A2 轴线电压分布图 Fig. A2 Axis voltage distribution diagram |
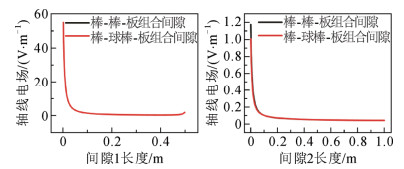
|
图 A3 轴线电场分布图 Fig. A3 Axis electric field distribution diagram |
|
|
表 B1 不同Nstab值下放电电压对比 Table B1 Comparison of discharge voltage under different Nstab value |
|
|
表 B2 不同Est值下放电电压对比 Table B2 Comparison of discharge voltage under different Est value |
|
|
表 B3 不同K值下放电电压对比 Table B3 Comparison of discharge voltage under different K value |
|
|
表 B4 不同Q0值下放电电压对比 Table B4 Comparison of discharge voltage under different Q0 value |
|
|
表 B5 不同qL值下放电电压对比 Table B5 Comparison of discharge voltage under different qL value |
|
|
表 B6 不同参数值下放电时刻对比(间隙1长度0.3 m) Table B6 Comparison of discharge time under different parameters (0.3 m of gap 1) |
|
|
表 B7 不同参数值下放电时刻对比(间隙1长度1.2 m) Table B7 Comparison of discharge time under different parameters (1.2 m of gap 1) |
| [1] |
张秋实, 王力农, 方雅琪, 等. 等电位人员-杆塔构架间隙放电特性仿真分析方法[J]. 电工技术学报, 2019, 34(11): 2415-2423. ZHANG Qiushi, WANG Linong, FANG Yaqi, et al. Discharge characteristics simulation method of equipotential worker-tower structure gap[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2415-2423. (  0) 0) |
| [2] |
胡毅, 王力农, 刘凯, 等. 特高压交流输电线路带电作业现场应用试验[J]. 高电压技术, 2009, 35(9): 2053-2058. HU Yi, WANG Linong, LIU Kai, et al. On-site application test of live working of UHV AC transmission line[J]. High Voltage Engineering, 2009, 35(9): 2053-2058. (  0) 0) |
| [3] |
胡毅, 王力农, 刘凯, 等. 1 000 kV交流输电线路带电作业组合间隙研究[J]. 电力设备, 2007, 8(8): 1-5. HU Yi, WANG Linong, LIU Kai, et al. Research on live working complex gap for 1 000 kV AC transmission lines[J]. Electrical Equipment, 2007, 8(8): 1-5. (  0) 0) |
| [4] |
胡毅, 刘凯, 王力农, 等. 1 000 kV同塔双回输电线路带电作业技术试验研究[J]. 高电压技术, 2010, 36(11): 2668-2673. HU Yi, LIU Kai, WANG Linong, et al. Experimental research of live working on 1 000 kV double circuit AC transmission line on the same tower[J]. High Voltage Engineering, 2010, 36(11): 2668-2673. (  0) 0) |
| [5] |
王万昆, 蓝磊, 安韵竹等. 组合空气间隙放电路径选择性试验[J]. 高电压技术, 2017, 43(11): 3800-3808. WANG Wankun, LAN Lei, AN Yunzhu, et al. Experiment on selectivity of discharge path of combined air gap[J]. High Voltage Engineering, 2017, 43(11): 3800-3808. DOI:10.13336/j.1003-6520.hve.20171031041 (  0) 0) |
| [6] |
王胜辉, 杨广华, 陈维江, 等. 含有电位悬浮导体的组合空气间隙放电特性实验研究[J]. 高压电器, 2018, 54(4): 1-7. WANG Shenghui, YANG Guanghua, CHEN Weijiang, et al. Experimental study on discharge characteristics of combined air gap with floating potential conductor[J]. High Voltage Apparatus, 2018, 54(4): 1-7. (  0) 0) |
| [7] |
朱真兵, 王欣, 张恒志, 等. 含悬浮金属板的棒-板-棒组合间隙操作冲击放电特性研究[J]. 电瓷避雷器, 2020(1): 29-35. ZHU Zhenbing, WANG Xin, ZHANG Hengzhi, et al. Study on switching impulse discharging characteristics of rod-plate-rod combination gap with potential suspension metal plate[J]. Insulators and Surge Arresters, 2020(1): 29-35. (  0) 0) |
| [8] |
WU S C, WANG L N, GAO J C, et al. Breakdown characteristics of combined air gaps under lightning impulse[J]. AIP Advances, 2022, 12(3): 035024. DOI:10.1063/5.0084951 (  0) 0) |
| [9] |
邵天颖, 梅红伟, 曾向君, 等. 含悬浮导体的棒板间隙工频击穿特性[J]. 高电压技术, 2021, 47(3): 1046-1054. SHAO Tianying, MEI Hongwei, ZENG Xiangjun, et al. AC breakdown characteristics of rod-plane gap with floating conductor[J]. High Voltage Engineering, 2021, 47(3): 1046-1054. DOI:10.13336/j.1003-6520.hve.20191932 (  0) 0) |
| [10] |
杨跃光, 苏俊源, 孙泽中, 等. 棒-板-棒组合间隙雷电冲击特性试验研究[J]. 电瓷避雷器, 2020(3): 68-73, 80. YANG Yueguang, SU Junyuan, SUN Zezhong, et al. Experiment investigation on breakdown characteristics of rod-plate-rod gap under lightning impulse voltage[J]. Insulators and Surge Arresters, 2020(3): 68-73, 80. (  0) 0) |
| [11] |
GAO J C, WANG L N, WU S C, et al. Breakdown characteristics of a long air gap containing a floating conductor under positive switching impulse[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2022, 29(5): 1913-1922. DOI:10.1109/TDEI.2022.3201780 (  0) 0) |
| [12] |
SCHNEIDER H M, TURNER F J. Switching-surge flashover characteristics of long sphere-plane gaps for UHV station design[J]. IEEE Transactions on Power Apparatus and Systems, 1975, 94(2): 551-560. DOI:10.1109/T-PAS.1975.31883 (  0) 0) |
| [13] |
PARIS L. Influence of air gap characteristics on line-to-ground switching surge strength[J]. IEEE Transactions on Power Apparatus and Systems, 1967, PAS-86(8): 936-947. DOI:10.1109/TPAS.1967.291917 (  0) 0) |
| [14] |
PARIS L, CORTINA R. Switching and lightning impulse discharge characteristics of large air gaps and long insulator strings[J]. IEEE Transactions on Power Apparatus and Systems, 1968, PAS-87(4): 947-957. DOI:10.1109/TPAS.1968.292069 (  0) 0) |
| [15] |
GALLET G, BETTLER M, LEROY G. Switching impulse results obtained on the outdoor testing area at renardieres[J]. IEEE Transactions on Power Apparatus and Systems, 1976, 95(2): 580-585. DOI:10.1109/T-PAS.1976.32138 (  0) 0) |
| [16] |
MOSCH W, LEMKE E, LARIONOV V P, et al. An estimation of the voltage-time characteristic of long rod plane gaps in air at positive switching impulse voltages[C]//Proceedings of the 13th International Conference on Phenomena in Ionized Gases. Berlin, Germany: IEEE, 1977: 427-430.
(  0) 0) |
| [17] |
RIZK F A M. A model for switching impulse leader inception and breakdown of long air-gaps[J]. IEEE Transactions on Power Delivery, 1989, 4(1): 596-606. DOI:10.1109/61.19251 (  0) 0) |
| [18] |
ABDEL-SALAM M, AL-ABDUL-LATIF U S. Simulation of Energized Franklin Rods for Lightning Protection[J]. IEEE Transactions on Industry Applications, 1997, 33(3): 651-659. DOI:10.1109/28.585854 (  0) 0) |
| [19] |
DIAZ R R, RUHLING F, HEILBRONNER F, et al. The corona inception under negative impulse voltage in inhomogeneous fields[C]//Proceedings of the 11th International Symposium on High Voltage Engineering. London, UK: IET, 1999: 155-158.
(  0) 0) |
| [20] |
GALLIMBERTI I. The mechanism of the long spark formation[J]. Le Journal de Physique Colloques, 1979, 40(C7): C7-193-C7-250. DOI:10.1051/jphyscol:1979795 (  0) 0) |
| [21] |
BONDIOU A, GALLIMBERTI I. Theoretical modelling of the development of the positive spark in long gaps[J]. Journal of Physics D: Applied Physics, 1994, 27(6): 1252-1266. DOI:10.1088/0022-3727/27/6/024 (  0) 0) |
| [22] |
ALEKSANDROV N L, BAZELYAN E M, D'ALESSANDRO F, et al. Numerical simulations of thunderstorm-induced corona processes near lightning rods installed on grounded structures[J]. Journal of Electrostatics, 2006, 64(12): 802-816. DOI:10.1016/j.elstat.2006.02.001 (  0) 0) |
| [23] |
GOELIAN N, LALANDE P, BONDIOU-CLERGERIE A, et al. A simplified model for the simulation of positive-spark development in long air gaps[J]. Journal of Physics D: Applied Physics, 1997, 30(17): 2441-2452. DOI:10.1088/0022-3727/30/17/010 (  0) 0) |
| [24] |
谢耀恒, 贺恒鑫, 陈维江, 等. 操作冲击下正极性长间隙放电物理仿真模型[J]. 中国电机工程学报, 2013, 33(31): 177-184. XIE Yaoheng, HE Hengxin, CHEN Weijiang, et al. A physical model to simulate long air gap discharge at positive switching impulse voltage[J]. Proceedings of the CSEE, 2013, 33(31): 177-184. (  0) 0) |
| [25] |
王力农, 胡毅, 刘凯, 等. 特高压输电线路带电作业组合间间隙的放电机理[J]. 高电压技术, 2011, 37(5): 1224-1231. WANG Linong, HU Yi, LIU Kai, et al. Complex gap discharge mechanism of live working on ultra high voltage transmission lines[J]. High Voltage Engineering, 2011, 37(5): 1224-1231. (  0) 0) |
| [26] |
GAO J C, WANG L N, WU S C, et al. Prediction of breakdown voltage of equipotential live-line work air gaps in transmission lines: a computational discharge model[J]. IEEE Transactions on Electromagnetic Compatibility, 2022, 64(6): 1932-1940. DOI:10.1109/TEMC.2022.3193203 (  0) 0) |
| [27] |
GAO J C, WANG L N, WU S C, et al. Effect of a floating conductor on discharge characteristics of a long air gap under switching impulse[J]. Journal of Electrostatics, 2021, 114: 103629. DOI:10.1016/j.elstat.2021.103629 (  0) 0) |
| [28] |
高嘉辰, 丁同殊, 方雅琪, 等. 正极性操作冲击电压下含悬浮导体长空气间隙放电发展过程[J]. 高电压技术, 2024, 50(4): 1664-1672. GAO Jiachen, DING Tongshu, FANG Yaqi, et al. Development process of discharges in long air gaps containing a floating conductor under positive switching impulses[J]. High Voltage Engineering, 2024, 50(4): 1664-1672. DOI:10.13336/j.1003-6520.hve.20230932 (  0) 0) |
| [29] |
GALLIMBERTI I, BACCHIEGA G, BONDIOU-CLERGERIE A, et al. Fundamental processes in long air gap discharges[J]. Comptes Rendus Physique, 2002, 3(10): 1335-1359. (  0) 0) |
| [30] |
BECERRA M, COORAY V. A self-consistent upward leader propagation model[J]. Journal of Physics D: Applied Physics, 2006, 39(16): 3708-3715. (  0) 0) |
| [31] |
BALDO G, GALLIMBERTI I, GARCIA H N, et al. Breakdown phenomena of long gaps under switching impulse conditions influence of distance and voltage level[J]. IEEE Transactions on Power Apparatus and Systems, 1975, 94(4): 1131-1140. (  0) 0) |
| [32] |
AREVALO L, WU D, JACOBSON B. A consistent approach to estimate the breakdown voltage of high voltage electrodes under positive switching impulses[J]. Journal of Applied Physics, 2013, 114(8): 083301. (  0) 0) |
| [33] |
RIZK F A M. Effect of floating conducting objects on critical switching impulse breakdown of air insulation[J]. IEEE Transactions on Power Delivery, 1995, 10(3): 1360-1370. (  0) 0) |
| [34] |
中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 高电压试验技术第1部分: 一般定义及试验要求: GB/T 16927.1—2011[S]. 北京: 中国标准出版社, 2012. General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, Standardization Administration of the People's Republic of China. High-voltage test techniques-Part 1: general definitions and test requirements: GB/T 16927.1—2011[S]. Beijing, China: Standards Press of China, 2012. (  0) 0) |
| [35] |
VILJOEN R A. Flashover performance of a rod-rod gap containing a floating rod under switching impulses with critical and near critical times to crest[D]. Johannesburg, South Africa: University of the Witwatersrand, 2008.
(  0) 0) |
| [36] |
阮江军, 唐烈峥, 邱志斌, 等. 基于流注起始判据的球-板-球短空气间隙击穿电压计算[J]. 高压电器, 2017, 53(7): 38-44. RUAN Jiangjun, TANG Liezheng, QIU Zhibin, et al. Breakdown voltage calculation of short sphere-plane-sphere air gap based on streamer inception criteria[J]. High Voltage Apparatus, 2017, 53(7): 38-44. (  0) 0) |
| [37] |
AREVALO L, COORAY V. Streamer to leader transition criteria for propagation of long sparks and lightning leaders[C]//Proceedings of 2014 International Conference on Lightning Protection. Shanghai, China: IEEE, 2014: 480-483.
(  0) 0) |
| [38] |
吴传奇. 冲击电压下长空气间隙正极性流注放电特性研究[D]. 武汉: 华中科技大学, 2014. WU Chuanqi. Research on the characteristics of long air gap positive streamer discharge under impulse voltage[D]. Wuhan, China: Huazhong University of Science and Technology, 2014. (  0) 0) |
| [39] |
赵贤根. 正极性冲击电压下长空气间隙流注茎特性研究[D]. 武汉: 华中科技大学, 2017. ZHAO Xiangen. Research on characteristics of the stem in long air gap discharges under positive impulse voltage[D]. Wuhan, China: Huazhong University of Science and Technology, 2017. (  0) 0) |
| [40] |
中华人民共和国国家质量监督检验检疫总局, 中国国家标准化管理委员会. 电力安全工作规程电力线路部分: GB 26859—2011[S]. 北京: 中国标准出版社, 2012. General Administration of Quality Supervision, Inspection and Quarantine of the People's Republic of China, Standardization Administration of the People's Republic of China. Safety code of electric power industry-Part of electric lines: GB 26859—2011[S]. Beijing, China: Standards Press of China, 2012. (  0) 0) |




 伍绍铖,1998—,男,博士生,主要从事空气间隙放电模型方面的研究工作;
伍绍铖,1998—,男,博士生,主要从事空气间隙放电模型方面的研究工作; 高嘉辰,1995—,男,博士,主要从事外绝缘、长空气间隙放电方面的研究工作;
高嘉辰,1995—,男,博士,主要从事外绝缘、长空气间隙放电方面的研究工作; 王官健,2000—,男,研究方向为外绝缘试验和输电线路检修等;
王官健,2000—,男,研究方向为外绝缘试验和输电线路检修等; 宋斌,1970—,男,博士,副教授,研究方向为电气设备状态检修等
宋斌,1970—,男,博士,副教授,研究方向为电气设备状态检修等