文献标识码: A
2. 南京理工大学自动化学院, 南京 210094;
3. 国网江苏省电力有限公司电力科学研究院, 南京 211103;
4. 智能电网保护和运行控制国家重点实验室, 南京 211106
2. School of Automation, Nanjing University of Science and Technology, Nanjing 210094, China;
3. State Grid Jiangsu Electric Power Company Electric Power Science Research Institute, Nanjing 211103, China;
4. Smart Grid Protection and Operation Control National Key Laboratory, Nanjing 211106, China
在“碳达峰、碳中和”的愿景驱动下,构建含高比例可再生能源的新型电力系统是实现该目标的重要措施之一。因此,基于变流器接口的机组(converter-interfaced generators, CIG)接入容量与占比将进一步提高[1]。以风电、光伏为代表的可再生能源发电机组通过电力电子器件并网,并采用最大功率跟踪控制导致其无法为系统提供转动惯量支撑,造成新型电力系统局部惯量缺失与整体惯量水平降低[2]。中国电科院基于“同步机电源转子动能与电源总容量之比”的方式预测我国电网的惯性时间常数在2030年将小于2 s[3]。在ENTSO-E预测的可再生能源渗透场景下,西欧部分国家的电网在2040年左右接近零惯量系统[4]。而冰岛、挪威等已经构建含极高比例可再生能源的电力系统[5],惯量缺失与不足已成为显著的系统化特征。
近年来,因系统惯量不足已引发多起严重的频率事件[6-7]。在南澳“9·28”停电事故中,因受台风影响导致456 MW的风机脱网从而引发后续一系列保护装置动作,最终在0.4 s内系统的频率由49.5 Hz急速跌落至47 Hz,系统惯量不足是事故的主要原因之一。在英国“8·9”频率事件中,较大的频率变化率触发分布式电源保护从而切除350 MW的分布式电源,而电网自身具有的频率调节能力无法满足功率缺额,进一步触发低频减载装置动作,最终被迫切出部分负荷引发停电事故。中国的“9·19”锦苏直流闭锁事故导致华东电网频率在12 s内由49.97 Hz跌落至49.56 Hz。小负荷场景下同步机电源开机规模较小导致转动惯量不足是频率快速下降的主要原因之一。
为了应对惯量不足给新型电力系统带来的严峻挑战,国内外学者以及行业从业人员主要围绕以下3个关于惯量的问题展开深入研究:1) 准确量化评估与获取系统等效惯量水平及变化趋势是保障低惯量电力系统频率安全首先需解决的关键问题;2) 明确当前等效惯量水平是否满足预想扰动下系统的惯量需求是保障系统频率安全的又一重要问题;3) 兼顾系统频率安全性与系统运行经济性对等效惯量进行合适的优化、配置与调度以满足惯量需求亦是低惯量电力系统迫切需要解决的问题。
新型电力系统的等效惯量评估、需求及优化已成为学术界与工业界共同关切的热点问题,相关学者与行业从业人员已取得一定的研究进展与成果,为解决新型电力系统的惯量相关问题提供了重要参考。为了更清晰地刻画等效惯量评估、需求及优化在新型电力系统中的定位、功能与挑战,本文针对上述问题的研究成果与进展进行综述,首先,在能量视角下诠释系统等效惯量的概念与组成。其次,为准确感知单体设备与系统整体的等效惯量支撑能力,根据电源同步方式及扰动类型对当前惯量评估方法进行分类阐述。然后,为提升系统频率运行的安全性,从系统惯量需求与优化两方面对低惯量电力系统的研究路径及现状进行归纳。最后,对有待深入研究的方向进行了展望。
1 新型电力系统等效惯量概念及其组成 1.1 等效惯量概念的理解根据牛顿运动定律可知,惯性作为物体(能量)的基本与固有属性,其外在表现为抵抗物体(能量)状态发生变化的能力。在以同步机电源为主导的电力系统中,惯性可由同步机电源转子所具有的旋转动能刻画。惯量表示定量刻画惯性的量度,在电力系统中一般采用惯性时间常数(s)或者旋转动能(MW·s)对其进行表征。因此,同步机的惯性时间常数可描述为下式:
| $ {H_{{\text{sg}}}} = \frac{{{J_{{\text{sg}}}}{\varOmega ^2}}}{{2{S_{{\text{sg}}}}}} $ | (1) |
式中:Hsg为同步机的惯性时间常数;Jsg为转动惯量;Ssg为额定容量;Ω为额定机械角速度。
在系统发生有功扰动时,系统不平衡功率与频率之间的关系可由系统等效摇摆方程刻画,如下式所示:
| $\left\{\begin{array}{l} \frac{\mathrm{d} \delta}{\mathrm{~d} t}=(\omega-1) \omega_{\mathrm{n}} \\ 2 H \frac{\mathrm{~d} \omega}{\mathrm{~d} t}=P_{\mathrm{m}}-P_{\mathrm{e}}=\Delta P_{\mathrm{dis}} \approx T_{\mathrm{m}}-T_{\mathrm{e}}=\Delta T \end{array}\right. $ | (2) |
式中:H为系统惯量;Pm为扰动期间总的机械输入功率;Pe为扰动期间总的电磁输出功率;ΔPdis为系统发生扰动时的不平衡功率;ω为系统角频率;ωn为系统额定角频率;δ为功角;
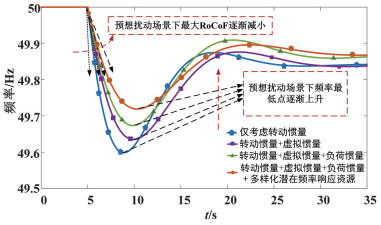
在构建以新能源为主体的新型电力系统进程中,若不考虑虚拟惯量的支撑作用将会导致电网运行与规划人员无法准确掌握整个系统的真实惯量水平,同时,还需要考虑多样化的频率响应资源对系统等效惯量的潜在贡献[8]。多样化潜在频率响应资源是指:对降低系统频率变化率与频率偏差具有正向作用的调频资源,但作用机理与转动惯量、虚拟惯量及负荷惯量又存在不同之处。例如快速频率响应控制、直流调制等可有效提升系统的频率最低点,但作用机理与等效惯量不同。例如华东电网直流输电工程中的直流调制模块在检测到有功损失超过设定门槛值时,立即增发一定的有功功率,从而快速减小不平衡功率,在一定程度上可视为等效增大系统的惯量。图 1为预想扰动下多类型惯量及多样化潜在频率响应资源对系统最大频率变化率(rate of change of frequency,RoCoF)与频率最低点的影响。
|
图 1 多类型惯量及多样化频率响应资源对RoCoF及频率最低点的影响 Fig. 1 Influence of multiple types of inertia and frequency response resources on RoCoF and the frequency nadir |
在单机无穷大系统中,增大同步机组的转动惯量(或惯性时间常数)有利于降低功角变化速度,提升单机无穷大系统的暂态稳定水平。同时,可基于实际切除时间的直接法判断系统暂态是否稳定,根据能量函数确定的故障切除极限允许时间tex可描述为下式:
| $ {t_{{\text{ex}}}} = \sqrt H \cdot \sqrt {\frac{{4({\delta _{{\text{ex}}}} - {\delta _0})}}{{{P_{{\text{me}}}}{\omega _{\text{n}}}}}} $ | (3) |
式中:δex为故障极限切除角;δ0为初始功角;Pme为同步机组机械功率。由式(3)可知系统惯量水平越低,故障切除极限允许时间越短。在单机无穷大系统中,系统整体惯量水平的降低可能会导致系统暂态稳定性能遭到恶化。
在暂态动态特性更为复杂的两机互联系统中,系统的惯量对故障所积蓄的暂态能量产生较大影响。基于暂态能量函数分析两机互联系统的研究成果表明:惯量的增大(或减小)对于送端、受端系统的暂态性能产生明显不同的影响。同时,在系统不同的负荷水平、初始工况以及运行方式下,两端系统的惯量水平对系统暂态稳定水平的影响具有明显的区别,甚至截然相反。
通过变流器设备引入的虚拟惯量可有效提升系统的惯量水平,但通过变流器设备(如双馈风机)提供的虚拟惯量对系统功角稳定产生显著的影响,如双馈风机基于df/dt(或RoCoF)的虚拟惯量对等值互联系统功角稳定的影响与功角首摆方向有关;含df/dt虚拟惯量的双馈风机接入超前机群时有利于提升系统暂态稳定性,接入滞后机群时则会恶化暂态稳定性。可以明确的是,由于虚拟惯量的不确定性,更为深入的虚拟惯量对高比例新能源电力系统功角稳定的影响机制仍有待探索[9]。
虚拟惯量具体可细分为电流源型虚拟惯量与电压源型虚拟惯量。其中,电流源型虚拟惯量通过将电网的RoCoF引入到变流器有功控制外环中以改变有功参考值,从而在外部电网频率扰动时为其提供功率支撑,进而对外表现为具有一定的惯量支撑能力。换言之,电流源型虚拟惯量主要影响式(2)中的ΔPdis,其本质属于功率源。而且其响应速度相较于同步机的瞬时响应较慢,即存在一定的延时(100 ms左右)。不同于基于RoCoF的快速功率调节,电压源型虚拟惯量通过在变流器控制环节中引入转子摇摆方程以及电磁暂态方程(如虚拟同步机控制)获得,从而使变流器的等效惯量外特性与同步机惯量高度相似。换言之,电压源型虚拟惯量主要影响式(2)中的H。且电压源型虚拟惯量响应速度理论上与同步机的瞬时响应速度相同,可瞬时提供惯量支撑,从而遏制RoCoF的迅速变化。
与转动惯量、虚拟惯量相比,来自负荷的惯量较少。但在新型电力系统中,负荷侧惯量发挥的作用愈加明显,该部分的惯量不可忽略。因此,有必要明确源自负荷侧惯量的类型。异步电机动态负荷转动惯量是指:在外部频率发生变化时,电动机负荷主动向电网释放存储在转子上的动能,从而为电网提供惯量支撑,其性质与同步机惯量类似。静态负荷的电磁耦合等效惯量是指:在频率或电压发生变化时,静态负荷吸收的功率也发生相应的变化,从而减小系统的有功不平衡量,因此,也可对外表现出一定的惯量支撑能力[10]。
由上述分析知:能量是系统(或装置)具有惯性的本质原因,主要的区别是能量的来源各异。同时,由于能量不能突变的原因才使得系统(或装置)的状态呈现微分变化过程。故能量变化速度与系统(或装置)的惯性密切相关,如扰动初始阶段,调速器未起作用时,同步机可将转子具有的旋转动能快速释放至电网以弥补系统的能量缺额,则可说明同步机的转动惯量较大,反之则较小。又如含虚拟惯性控制的储能在短时间内向电网快速释放能量,从而说明其等效惯量支撑能力较强,反之则较弱。
综上所述,从能量变化角度来看,在系统主要调频方式响应时间尺度以内(时间尺度),新型电力系统等效惯量可表征为:在不平衡有功扰动场景下,系统基于多元形式的能量连续变化性质维持系统频率保持当前状态的能力,其组成包含同步机及异步电机的转动惯量、基于变流器控制的各类型虚拟惯量以及负荷电磁耦合等效惯量等。可描述为下式:
| $ \begin{aligned} & 2\left(H_{\mathrm{sg}}+H_{\mathrm{gfm}}\right) \frac{\mathrm{d} \omega}{\mathrm{~d} t}=\Delta P_{\mathrm{dis}}-\Delta \frac{\mathrm{d} E_{\text {muti }}(\omega(t))}{\mathrm{d} t} \\ & \Leftrightarrow 2\left(H_{\mathrm{sg}}+H_{\mathrm{gfm}}\right) \frac{\mathrm{d} \omega}{\mathrm{~d} t}=\Delta P_{\mathrm{dis}}-\Delta \frac{\mathrm{d} E_{\text {muti }}}{\mathrm{d} \omega} \frac{\mathrm{~d} \omega}{\mathrm{~d} t} \\ & \Leftrightarrow\left(2\left(H_{\mathrm{sg}}+H_{\mathrm{gfm}}\right)+\Delta \frac{\mathrm{d} E_{\text {muti }}}{\mathrm{d} \omega}\right) \frac{\mathrm{d} \omega}{\mathrm{~d} t}=\Delta P_{\mathrm{dis}} \\ & \Leftrightarrow H_{\mathrm{eq}}(t) \frac{\mathrm{d} \omega}{\mathrm{~d} t}=\Delta P_{\text {dis }} \end{aligned} $ | (4) |
式中:Heq(t)为系统等效惯量,具有一定的时变特性;Hgfm为电压源型虚拟惯量;ΔPdis为系统扰动功率;Emuti为多元形式的能量。
根据式(4)首先可知,多元形式的能量输入是导致系统等效惯量呈现时变特性的本质原因。需要说明的是,若以系统(或装置)具有的可用于惯量支撑的能量与某一基准值的比值作为系统的等效惯量,则等效惯量具有定值属性,该视角下的等效惯量与从系统固有属性角度分析惯量性质所得结果一致。若以可用于惯量支撑的能量当前水平与某一基准值的比值作为系统的等效惯量,则等效惯量具有时变属性。若系统内无多元形式的能量输入,即dEmuti/dt=0与Hgfm=0。式(4)与同步机的常规转子运动方程保持一致,Heq(t)转化为Hsg。因此,等效惯量依旧具有有功-频率范畴内的动力学性质。其次,单位时间内的能量变化(即能量变化速度)等价于功率。在扰动初期,能量变化速度越快,单位时间内释放(或吸收)的功率越大,越有利于弥补系统的功率缺额,系统频率变化率也就越小,故等效惯量也越大。基于此,等效惯量亦可用于描述惯量的空间分布特性,系统内部区域可用于惯量支撑的能量允许变化速度越快,则可说明该区域内等效惯量支撑能力越强,反之则越弱。
1.2 等效惯量组成部分传统电力系统等效惯量主要源自同步机组,少量来源于电动机动态负荷及其他静态负荷。而在以新能源为主体的新型电力系统中,系统等效惯量主要由虚拟惯量、转动惯量及静态负荷的电磁耦合等效惯量组成。转动惯量依旧主要源自同步机组与电动机动态负荷;虚拟惯量主要通过在基于变流器口的电源控制环节引入先进的模拟惯性控制获得,例如风光储、高压直流以及综合负荷等;电磁耦合等效惯量源自静态负荷。如图 2所示。

|
图 2 新型电力系统等效惯量组成部分 Fig. 2 Equivalent inertia components in power system |
准确获取新型电力系统单体设备的等效惯量支撑特性有利于从设备侧看待系统层面的等效惯量动态特性,同时,对于电网运行人员应对多类型低惯量场景问题具有重要意义。具有等效惯量支撑特性的设备主要包含同步机组、附加虚拟惯性控制的变流器机组以及异步电机动态负荷等。考虑到等效惯量主要源自同步机组与附加虚拟惯性控制的变流器非同步机组,少量来自于负荷侧,故本节首先重点对同步机组与非同步机组的等效惯量评估方法进行阐述与总结。
2.1 面向同步机及变流器电源的设备级等效惯量评估方法同步机组作为电力系统的主力电源,精准评估同步机的等效惯量与阻尼有利于保障系统频率的安全运行。评估同步机组等效惯量与阻尼的常规方法包含频域响应法、抛载试验法、主动短路试验法、甩负荷试验法等,但上述试验方法存在精度较差与花费较高的不足。伴随相量测量单元(phase measurement unit,PMU)在新型电力系统中的广泛布置,基于量测数据驱动的方法能够更加准确地评估同步机电源的等效惯量及阻尼。已有关于同步机参数评估的成果不仅仅关注惯量与阻尼参数,同时亦会对其他参数进行估计。由于同步机模型与励磁模型的非线性,基于群智算法的同步机模型多参数估计应用范围较广[11-12]。由于群智算法对同步机多参数估计存在着固有的不足,如参数选择不当影响算法收敛,文献[13]采用扩展卡尔曼滤波算法对高阶非线性同步机模型参数及惯量参数进行量化评估。上述研究成果由于估计参数较多,可能造成获取的同步机等效惯量参数准确度不够高。为解决这一问题,通过PMU获取同步机连续的电磁功率变化数据,从而可支撑惯量参数与其他类型参数的独立评估[14]。文献[15]基于卡尔曼滤波形式的转子运动方程,应用发电机端电压/电流相位的PMU数据与内部转子速度之间的关系,从而获取同步机电源的等效惯量时间常数。文献[16]采用动态模式分解与时域重构方法建立机电参数与系统特征的线性关系,从而通过求解线性方程获取同步机的等效惯量与阻尼。文献[17]结合受控自回归模型与最小二乘法两者的优点,提出根据二阶转子运动方程辨识高阶同步机等效惯量参数的方法。
综上所述,由于同步机模型明确且通过PMU获取量测数据难度较低,当前研究成果可较为准确地评估同步机电源向电网提供的等效惯量支撑。
基于变流器的非同步机电源在新型电力系统中的接入容量与占比逐渐升高,基于变流器的非同步机电源附加虚拟惯性控制可为系统提供一定的惯量支撑,而电网运行人员更希望量化非同步机电源单体设备的等效惯量对系统等效惯量的贡献。
在不考虑变流器具体的应用场景下,文献[18]基于传递函数推导含频率控制变流器的惯量支撑特性,同时分析控制环节与设计参数对变流器等效惯量的影响,提出适用于附加频率控制的变流器动态等效惯量评估方法。文献[19-21]考虑延时效应对变流器等效惯量造成的影响,分别基于差分转子运动方程与深度强化学习提出适用于变流器等效惯量连续评估的方法。而在大扰动场景下,结合虚拟同步机的端电压和电流相量测量值估计内部虚拟频率,进而推导出状态空间摇摆方程模型[22],再基于无迹卡尔曼滤波及数据驱动方式获取变流器电源的等效惯量大小。为进一步获取跟网型变流器的等效惯量,文献[23]采用以贝叶斯推理为基础的分层自适应重要性采样技术量化评估同步机及非同步机的等效惯量支撑能力。
在考虑变流器具体应用对象及控制特性(如风机、光伏及储能)的场景下,基于变流器的非同步机电源等效惯量不仅与变流器自身的控制方法及结构参数有关,而且也受变流器应用对象运行状态的影响。在感知风机的等效惯量支撑能力方面,基于模型驱动的思想,文献[24-27]详细推导了含附加虚拟惯性控制双馈风机的等效惯量评估方法,该法表明了含虚拟惯性控制的双馈风机对外部电网提供的等效惯量具有时变特性,并且与控制结构参数密切相关。考虑到双馈风机诸多控制参数并不易获得,可基于量测数据驱动的思想,分别结合受控自回归模型与能量守恒原理评估含虚拟惯性控制的双馈风场的等效惯量支撑能力[28-29]。类似地,文献[30]结合数据驱动与非参数核密度估计预测一定置信水平场景下的风电场等效惯量波动区间范围。为着重考虑风电机组的运行工况及风速的分布,文献[31]基于Copula函数与已建立的惯性功率估计模型获取一定置信度场景下的可用等效惯量区间。上述关于风电场的等效惯量评估方法均假设机械转矩未发生较大变化,但该假设易造成最终的评估结果不准确。基于此,文献[32]考虑风电机组的机械能损失,然后结合风速随机性与相关性构建风电场有效惯量时空分布评估模型。文献[33]基于频率响应模型,采用Routh近似法获得双馈风机虚拟惯性转矩的解析式,结合矩阵铅笔法与最小二乘评估风电场的等效惯量。在评估储能的等效惯量支撑方面,基于能量守恒原理,文献[34]提出适用于储能的等效惯量表征方法,该法表明基于变流器接口的储能等效惯量受变流器设备参数与储能本体两方面的约束。但通过直接构建储能等效惯量与控制结构参数的解析式表明:储能的等效惯量动态特性主要由荷电状态与外部系统频率变化决定[35-36]。
综上,不同于同步机惯量仅受自身转子质量的影响,基于变流器的非同步机组等效惯量受诸多因素影响,如自身控制方法、控制参数以及运行状态等。目前缺乏较为统一的评估方法获取非同步机组的等效惯量动态支撑特性。
2.2 面向系统层面的等效惯量评估方法电力系统层面的等效惯量评估作为保障系统频率安全的关键问题,相关学者与行业从业人员已取得一定的研究进展与成果,基于已取得的成果,从扰动类型角度对当前惯量评估方法进行分类阐述,并将系统等效惯量评估方法细分为:基于阶跃扰动的惯量评估方式、基于小扰动的惯量评估方式、基于类噪声扰动的惯量评估方式。
(1) 基于阶跃扰动的系统级等效惯量评估方法
基于阶跃扰动的惯量评估方式通过有功不平衡量与初始时刻RoCoF的比值确定系统等效惯量。如下式所示:
| $ {H_{{\text{sys}}}} = \frac{{\Delta {P_{\text{d}}}}}{{R\left| {_{t = {0^ + }}} \right.}} $ | (5) |
式中:ΔPd为阶跃扰动大小;
基于上述方法的核心思想,文献[37]应用区域系统主导机组的RoCoF与区域系统之间的联络线功率变化定量评估区域系统的惯量水平,进而获得整个系统的等效惯量水平。文献[38]基于高压直流输电系统传输功率的变化,并结合频率变化的PMU数据与能量估算方法获取系统的等效惯量。文献[39]分别对新能源机组、同步机及电压敏感性负荷进行独立惯量评估,并采用加权平均方式在阶跃扰动下获取整个系统的等效惯量。但上述研究成果过于依赖量测数据质量,且惯量评估结果与量测数据质量直接相关。
进一步,根据式(4)可知:基于阶跃扰动的惯量评估方式存在着获取扰动功率大小较难、扰动时刻不易确定以及初始RoCoF量测不准等不足。为实现有功功率扰动的准确检测,文献[40]基于决策树与受监控发电机组之间的同调性,并结合系统阻抗矩阵确定扰动的发生时刻、位置及大小。文献[41]根据RoCoF估计因同步机电源意外跳闸造成的有功功率损失大小,然后结合RoCoF与所得有功功率损失大小对系统惯量水平进行定量刻画。考虑到新型电力系统中的电力电子设备占比逐渐加大以及快速调频服务响应速度越来越快,为了提升系统等效惯量评估结果的准确性,有必要将快速调频及负荷功率动态特性纳入至扰动功率估计模型之中[42]。为了准确判定扰动发生时刻,可为RoCoF或频率波动设置一定的门槛值,当实际RoCoF或频率波动大于该门槛值时即可认定为扰动发生时刻,然后,采用基于阶跃扰动的惯量评估方式对系统惯量进行评估[43-44]。而文献[45]则是通过对频率量测数据进行二次微分以确定扰动的发生时刻,该法计算准确度相较于常规方法有所提升。为了提高扰动初始时刻RoCoF的量测精度,降低量测噪声信号对惯量评估结果的影响。文献[46]设计了中值滤波器对频率量测数据进行预处理,并基于最小二乘法提出RoCoF精确估算算法,并且该算法在夏威夷群岛电网中得到应用,为后续等效惯量评估奠定基础。不同于对频率数据直接进行处理,应用多项式拟合获取扰动后较短时刻内的频率变化趋势,然后对其微分获取RoCoF,从而在一定程度上可降低振荡分量带来的不利影响[47]。此外,新型电力系统的频率响应空间特性愈加明显,采用不同区域的频率数据进行惯量评估对最终的评估结果亦会产生较大影响[48]。
伴随构建新型电力系统的进程不断加快,虽然然上述基于阶跃扰动的惯量评估研究成果能够在一定场景下获得系统的等效惯量,但却无法刻画系统等效惯量的空间分布特性。为此,文献[49]提出分频器的概念,并结合系统等值转子运动方程与发电机节点的功率、频率量测数据实现对系统内各节点等效惯量的评估。在此基础上,为了能够涵盖非同步机电源的惯量评估,文献[50-51]提出基于节点功率变化率的惯量评估模型,可用于对所有类型的电源进行等效惯量评估,但该模型存在奇异值问题,极易导致数值不稳定。可通过引入符号函数解决上述模型的奇异值问题[52],但其主要应用于同步机或非同步机电源设备,是否适用于系统层面的惯量评估仍有待商榷。文献[53]计及电网结构及参数推导了简单系统与多机系统的节点计算惯量解析表达式,从而在阶跃扰动下获得系统惯量的分布特性。文献[54]根据阶跃扰动不平衡功率与节点RoCoF定义节点等效惯量,并基于转子运动方程与频率空间特性获取节点等效惯量的解析式,并为其确定了应用场景。文献[55]对阶跃扰动下的惯量时空特性进行深入地剖析,所提节点惯量表征形式较为全面地刻画系统惯量的空间分布特性。文献[56]通过对阶跃扰动场景下的PMU量测功率、频率数据进行二阶罚函数数据预处理,提出基于二阶罚函数自适应变阶拟合的惯量空间分布特性感知方法,实现了对等效惯量空间特性的有效刻画。
综上所述,基于阶跃扰动的惯量评估方式较为适合以同步机电源为主导的传统电力系统,但该种评估方式面临着获取扰动功率大小较难、扰动时刻不易确定以及初始RoCoF量测不准等挑战,同时也无法连续获取系统的等效惯量评估结果。
(2) 基于小扰动的系统级等效惯量评估方法
基于小扰动的惯量评估方式可在一定程度上避免基于阶跃扰动惯量评估方式的不足。文献[57]立足于新型电力系统含高比例可再生能源的特征,提出基于斜坡渐变扰动的系统等效惯量评估方法,该法中的斜坡扰动相较于阶跃扰动在可观性与可测性方面具有明显的优势。当系统发生小扰动时,一般会产生机电振荡,而振荡频率、阻尼比与惯量存在直接联系。因此,也可通过摇摆方程构建固有机电振荡参数与系统惯量之间的联系从而对系统进行惯量评估[58],例如基于自适应迭代滤波分解方法获取振荡频率与阻尼比,进而获取复杂电网的等效惯量[59]。在此基础上,也可结合动态模式分解算法与数据驱动方法实现互联电网的分区惯量评估[60]。类似地,文献[61]应用坐标变换识别振荡模态,从而提出适用于高比例新能源系统的惯量评估方法。不同于上述方法,文献[62]则是基于小幅值探针信号在机电频带具有较强的幅值特征,结合闭环辨识算法与系统频率响应模型获取系统的等效惯量,从而进一步提高了惯量评估结果的准确性,基于此,英国Reactive Technologies公司开发了GridMetrix用于对系统等效惯量进行评估,并在英国与日本电网中取得应用。不同于上述方法侧重获取系统的整体等效惯量,为了在小扰动下获取等效惯量在系统中的分布情况,文献[63]通过输出误差模型建立惯量空间分布模型,并基于多新息辨识理论获取所构建模型的待辨识参数,从而评估系统的惯量分布情况。文献[64]基于小扰动下的频率量测数据与系统电源参数定义节点等效惯量,并通过自适应多项式拟合方法获取小扰动下的节点等效惯量。文献[65]基于阻抗与对应频率响应之间的近似关系,提出一种在小扰动下非侵式电源节点惯量评估方法,该法可有效获取同步机/非同步机电源节点的等效惯量与一次调频支撑能力。文献[66]基于图论和节点惯性指数分析电力系统中节点惯性的时空分布特征,并结合菲德勒向量提出动态响应指数,全面分析节点惯性的时空分布特征及其对系统动态响应的影响。
综上,基于小扰动的惯量评估方式虽然可在一定程度上减轻对频率事件中阶跃扰动的依赖,但是依旧无法实现系统等效惯量的连续评估,通过人为主动地向系统注入小扰动的方式亦容易触发继电保护的误动作。同时,基于小扰动的惯量评估方式较难刻画等效惯量的时空分布特性对最终评估结果造成的影响。
(3) 基于类噪声扰动的系统级等效惯量评估方法
为了在准稳态下场景下连续获取系统等效惯量,亦为降低对频率事件阶跃扰动的依赖,基于类噪声扰动的系统等效惯量评估方法应运而生[67-68]。通用电气数字集团(GE Digital)开发了有效惯量评估及预测系统,该系统无需额外注入扰动信号,基于已布置的PMU获取量测数据,并运用相应的AI技术实现基于类噪声扰动的电网惯量常态化在线估计与预测,但该系统目前的应用受制于PMU在电网中的部署范围。文献[69]推导类噪声扰动与频率功率谱密度之间的关系,并结合非线性最小二乘拟合方法提出适用于新能源电力系统的等效惯量评估方法。文献[70]基于类噪声扰动数据的协方差矩阵,并结合模型拟合方法获取系统的等效惯量。基于系统辨识理论,将系统等效惯量视作待辨识量是连续获取等效惯量的重要方法。以PMU获取的电源母线处功率变化数据作为输入量、系统频率偏差数据作为输出量,结合迭代方程误差模型[71]、受控自回归模型[72]、递归最小二乘法[73]、动态回归扩展方法[74],获得降阶的系统频率响应模型,最后在降阶模型中提取出系统等效惯量信息。不同于基于系统辨识理论的等效惯量评估方法,在类噪声扰动场景下,基于数据驱动及人工智能的方法在惯量评估方面体现的优势逐渐引起众多学者的关注。基于功率谱分析和输入-输出相关性,文献[75]明确了神经网络训练在电力系统连续等效惯量评估方面所需的正确输入特征。通过构建随机动态模型[76]、局部合理模型[77],应用数据驱动方式和类噪声扰动数据也可获取含高比例非同步机电源系统的等效惯量。
上述成果虽然可在一定程度上连续获取系统的等效惯量,但无法充分体现含高比例电力电子设备的新型电力系统等效惯量空间分布特性。因此,基于类噪声扰动开展区域级与节点级的等效惯量评估十分必要。文献[78]将区域级系统等效惯量评估问题转化为非线性参数辨识问题,应用区域间等效频率动态模型在类噪声扰动场景下获取系统的等效惯量水平。为进一步刻画等效惯量的空间特性,可基于分频器理论推导转子转速与网络母线频率之间的关系,并结合类噪声扰动数据量化电源母线的等效惯量水平[79]。通过定义节点惯量[80],然后基于类噪声扰动和频率频谱也可将系统等效惯量的时空特性进行直观的可视化处理。
综上,上述方法同样较为依赖量测数据,并且需要在系统内布置足够的数据量测装置。同时,基于类噪声扰动的系统惯量评估方法较难考虑各种类型虚拟惯量(尤其是电流源型虚拟惯量)对系统等效惯量的贡献,同时也面临着评估结果精度低以及鲁棒性较差等问题。未来有待进一步探索考虑多类型虚拟惯量运行特性及不确定性因素的系统等效惯量评估方法。基于3种类型扰动的惯量评估方式核心原理、优缺点及适用场景总结如表 1所示
|
|
表 1 基于3种类型扰动的惯量评估方式对比分析 Table 1 Comparative analysis of inertia estimation methods based on three types of disturbances |
在完成系统等效惯量评估的基础上,还需进一步明确当前惯量水平能否保障系统在预想极限扰动场景下的频率安全[81],如不能,则需要确定所需的惯量缺额便于为后续的惯量补偿奠定基础。当前,常用于刻画惯量需求的指标有非同步机电源渗透率Rsnsp、惯量比Rir、安全运行惯量Esec、最小惯量阈值Ecri、最小惯性常数Hcri。不同指标之间的定义、数学模型及优缺点对比如表 2所示。
|
|
表 2 不同惯量需求刻画指标对比分析 Table 2 Comparative analysis of different inertia demand characterization indicators |
非同步机电源渗透率Rsnsp与惯量比Rir是最初用于量化描述惯量安全的指标[82],但两者存在着表达形式不够直观的不足,且无法计及系统调频能力对惯量需求的影响。爱尔兰电网运营商强制要求含高比例再生能源接入系统的惯量水平不能过低[83],分别将Rsnsp和Rir设置为75%和30 s。相较于Rsnsp和Rir,Esec与Ecri能够直观描述RoCoF指标约束下的系统惯量需求,但无法充分体现惯量的时变特性与系统调频能力,同时无法刻画频率偏差约束对系统惯量需求造成的影响。南澳电网将Esec与Ecri分别设置为6000 MW·s与4400 MW·s;《电力系统惯量支撑和一次调频能力技术要求》征求意见稿要求系统在遭受10%负荷容量损失场景下,系统惯性常数不得小于3 s,即Hcri必须大于1.5 s[84]。
考虑到上述刻画惯量需求指标存在的不足,因此,引入临界惯量需求(critical inertia requirements, CIR)的概念。由于惯量仅与RoCoF、最大频率偏差有关系,故可通过RoCoF约束与频率偏差约束间接获取临界惯量需求。因此,临界惯量需求可定义为:在预想极限扰动情况下,系统确保RoCoF与最大频率偏差在可接受范围内所需要的最小惯量水平[85],即惯量的阈值。换言之,当系统惯量水平大于CIR时,系统在预想极限扰动下的RoCoF与最大频率偏差均可保持在安全范围之内。
目前,电力系统的CIR评估较为依赖调控人员的运行经验,缺乏科学的定量分析与理论支撑。通过分析已有的研究成果可知:系统的CIR主要通过考虑系统的频率偏差与RoCoF两个频率动态指标安全约束而获得。例如通过具体的不平衡功率大小与RoCoF约束之间的比值关系确定系统的临界惯量需求[86-87]。类似地,文献[88]应用具体的分布式电源防孤岛RoCoF保护阈值确定惯量约束,并提出含惯量约束的经济调度模型,但未考虑频率响应的空间分布特性。以调度序列中的最大机组意外跳闸作为预想极限扰动,文献[89]依据RoCoF约束量化2050年前欧洲电力系统对额外惯量的预期最大需求。文献[90]引入基于多时间尺度的RoCoF约束,并建立系统节点临界惯量需求计算模型。不同于上述研究成果,文献[91-93]首先基于RoCoF约束获取系统的临界惯量需求,但着重制定风储联合快速频率响应控制策略以及系统规划运行方案,以实现提升系统频率运行安全性的目的。
最大频率偏差作为描述频率动态安全的另一个关键指标。仅计及RoCoF约束,不考虑最大频率偏差对临界惯量需求的影响,易造成临界惯量需求评估结果不准确[94]。因此,文献[95-96]分析了不同惯量水平下的频率曲线,发现随着惯量水平的提高最大频率偏差减小。文献[97]基于频率动态模型推导了系统惯量与最大频率偏差之间的非线性关系。在此基础上,为了便于应用频率偏差与惯量之间的关系,文献[98]基于近似求解方法量化了惯量对系统最大频率偏差的影响,从而可兼顾RoCoF约束与最大频率偏差约束对临界惯量需求的影响。聚焦微电网频率安全运行场景,文献[99-100]基于频率动态指标安全约束为微电网系统构建临界惯量需求评估模型,但未计及联络线功率的影响,较难应用于实际的互联电力系统。
在频率动态安全指标约束的基础上,为了满足电力系统在不同类型场景下的频率安全运行需求,还需进一步考虑多重影响因素对惯量需求造成的影响[101]。因此,文献[102]计及静态电压负荷对不平衡功率的影响、频率的分布特性、扰动的类型等因素,建立临界惯量需求评估模型,但并未给出求解临界惯量需求的通用方法。文献[103-104]则是在频率安全约束的基础上提出计及多元虚拟惯量支撑能力的临界惯量需求评估模型。考虑到异步电动机动态负荷对系统等效惯量的贡献[105],文献[106]通过构建含异步电机的系统频率响应模型,并基于频率安全约束提出计及异步电机频率特性的系统临界惯量需求评估方法。文献[107]建立含虚拟惯量及新能源渗透率的电力系统频率模型,并引入频率分布系数,结合频率安全指标约束构建系统的惯量需求评估模型。类似地,文献[108]构建含多类型机组与异步电机的系统频率响应模型,并结合频率安全指标约束对系统的最小惯量需求进行量化评估。
综上,上述研究主要在不同场景下考虑多类型影响因素并基于RoCoF约束、频率偏差约束获取系统的系统临界惯量需求,但对电力系统频率响应日益明显的空间特性考虑不足。基于变流器的非同步机电源高比例渗透导致系统频率响应空间特性愈加明显,将所研究系统等效处理成一个孤立整体的方式不能针对性地考虑局部可再生能源高渗透系统的真实临界惯量需求,从而导致获取的系统整体临界惯量需求并不十准确,亦无法进一步为惯量的准确补偿提供指导。
4 面向频率安全的系统等效惯量优化虽然基于频率偏差与RoCoF两个安全指标约束可获得系统的临界惯量需求,但临界惯量需求评估方法仅能获取系统或区域系统整体的临界惯量需求信息,如何在运行阶段优化旋转惯量与虚拟惯量满足系统的临界惯量需求,以进一步保障系统在一次调频时间尺度内的频率安全运行是迫切需要解决的关键问题。当前,惯量优化主要涉及两面的问题:一是嵌套频率安全约束的机组组合(unit commitment, UC)优化调度问题;二是基于空间特性的惯量优化布局。
4.1 含频率安全约束的系统优化运行当前,主要基于频率偏差与RoCoF两个安全指标约束获取系统的临界惯量需求,换言之,只要在预想扰动情况下将系统的RoCoF与频率偏差指标约束在安全阈值之内等价于系统等效惯量已满足临界惯量需求。该研究方向大致可划分为两大类,一类是充分挖掘系统内各种可用于惯量及频率支撑的资源,例如风光储可再生资源、需求侧响应等,将上述资源纳入至机组组合模型中以提升系统惯量支撑与频率响应的能力[109]。
为提高含规模化风电机组的系统频率运行经济性与安全性,文献[110]应用阶梯备用对构建的动态频率响应模型进行降阶处理,基于此,提出适用于高比例风电系统的日前日内运行方式。考虑到风电的不确定性,文献[111]提出频率指标全过程约束以满足系统不同阶段的整体惯量备用需求。文献[112-114]将频率最低点约束转换为原动机与调速器所释放功率约束,便于将其纳入至UC模型的约束条件之中,并兼顾风电的不确定性建立含有频率安全约束的UC模型,有效提升含高比例风电的系统频率运行安全性。为充分发挥调相机的惯量支撑特性,文献[115]基于惯量控制与有功备用机理,提出计及同步调相机与风电协同的分布鲁棒UC模型。文献[116]基于随机优化调度方法动态优化来自风机的虚拟惯量,从而提高系统频率运行的稳定性。
进一步,为保障多类型可再生能源渗透下的低惯量系统频率安全,并且兼顾系统经济性与安全性运行的需求。文献[117-118]计及多能源运行特性构建系统频率响应模型,基于此,建立含有频率安全约束的日前日内多时间尺度优化模型,有效促进了清洁能源的消纳。为了降低含频率安全约束的UC模型求解复杂度,文献[119-120]将UC模型解耦为临界惯量需求评估与系统调度优化,提出适用于含高比例新能源的电力系统机组组合运行策略,实现了系统惯量需求评估与UC优化调度模型的单独求解,并且该策略具有简单易行、线性化程度高的优点。文献[121]计及风光储多类型的虚拟惯量与调频特性,提出适用于含多类型虚拟同步机的微网优化调度模型,该调度模型可对系统整体备用与惯量不断进行修正以提升微电网在不同场景下的频率稳健运行能力。文献[122]提出一种适用于低惯量电网的随机UC调度模型,该模型通过场景树方法考虑不确定性,并将非线性的频率变化率与频率最低点约束转换为边界综合系统参数以提升算法的计算效率。文献[123]使用灵敏度法取代蒙特卡洛模拟实现快速计算目的,并提出通过概率评估的方式降低区域级电力系统RoCoF越限风险,从而保障低惯量系统的安全运行。文献[124]提出一种考虑频率约束的风火储协调规划模型用以为高比例可再生能源系统提供足够的频率支撑。类似地,文献[125]计及风储运行状态,将量化的风储频率支撑能力、备用容量需求与频率约束共同整合至优化调度模型之中,在满足频率安全约束的同时亦降低了低惯量系统运行的成本。针对风电的不确定性与尾流效应,文献[126]结合RoCoF与频率最低点两个动态频率安全指标提出考虑不确定性的调度方法与风电备用功率模型。考虑系统强度与惯量的双重需求,文献[127]基于故障电流求解器与系统强度因子,提出一种计及系统强度约束与惯量约束的机组组合调度方法,该调度方法可有效满足新能源电力系统对系统强度与惯量的需求。鉴于频率响应的空间特性日益明显,文献[128]立足于节点RoCoF约束,推导典型扰动下节点初始RoCoF的解析表达式,并获得节点初始RoCoF与发电机工作状态之间的关系,基于此,提出考虑频率动态响应空间分布特性的UC模型。
综上所述,在不同场景下将频率安全约束嵌入至机组组合模型以保障系统频率安全的方式,对含高比例可再生能源的电力系统频率安全运行具有重要借鉴意义。但当前将频率安全约束视作统一量的调度方式难以满足变流器电源高占比区域系统自身严格的频率安全要求,并且上述研究严重依赖系统调度手段,在日内充分发挥变流器电源虚拟惯量可控性与灵活性方面有所欠缺。
另一类则是侧重研究不同场景下的机组组合动态频率建模方法。基于系统频率安全指标的视角,不同场景下的UC动态频率响应建模方法主要包含:全过程动态频率约束、简化动态频率约束、稳态频率偏差约束、离散动态频率约束、基于仿真的动态频率约束。上述频率安全约束建模方法各自具有优缺点[129],系统动态频率响应建模方法需要根据不同场景选择合适的频率安全约束建模方法,以便更好地满足系统频率安全优化调度方法对计算效率与计算精度的要求。
4.2 基于空间特性的惯量优化布局可再生能源场站一般位于电力系统的末端,导致多类型电源之间的电气距离加大。鉴于新型电力系统的频率响应空间特性日益明显,如何借助非同步机组虚拟惯量的灵活性与可控性抑制节点频率的振荡,提高系统内节点频率的同调性逐渐成为研究热点。其主要思路为:建立系统的动态网络结构,同时构建含有节点频率的目标函数,基于李雅普诺夫方程获取各节点的最优惯量参数[130]。文献[131]应用矩阵摄动理论对系统的状态空间进行线性化处理便于降低后续的求解难度。文献[132]分析了跟网型与构网型变流器的动态特性差异,并构建了对应的优化模型,以充分优化跟网型与构网型变流自身参数及在系统中的位置。文献[133]基于临界频率下降和稳定裕度提出虚拟惯性规划方法,并采用李雅普诺夫函数简化并求解非凸优化问题。文献[134]基于惯性中心频率与节点频率之间的偏差,指导含有虚拟惯性控制的高压直流系统换流站的落点布局。上述研究成果的思路与广域阻尼控制相似,从小干扰稳定分析角度出发,通过改变系统主导模态的方式实现提升暂态特性的目的,但该方式难以计及变流器电源设备的虚拟惯量全过程支撑特性。
不同于上述成果,文献[135]基于分频器理论构建可反映频率空间特性的系统频率响应模型,结合节点惯量与节点动能概念建立大扰动场景下的虚拟惯量配置优化模型,实现了对虚拟惯量合适配置的目标。文献[136]基于缩减聚类提出节点惯量薄弱性评估方法,在此基础上,结合源网荷三侧资源构建考虑节点惯量的扩展规划模型。文献[137]采用频率响应的一致性方法对系统进行分区,然后基于RoCoF约束为分区配置合适的虚拟惯量。文献[138]基于Voronoi图重心建立系统的虚拟惯量数学模型,以判定矩阵的H2范数作为评价指标,并计及多类型因素对系统稳定性的影响,根据图重心法获取虚拟惯量配置的最优解。文献[139-140]应用与频率相关的暂态能量函数优化系统的虚拟惯量配置,从而提升系统频率运行的安全性。文献[141]计及各区域RoCoF与频率最低点的约束,提出以系统运行经济性为目标函数的储能虚拟惯性配置模型,但该模型较难抑制节点层面的频率波动。
综上,上述成果主要从小干扰稳定性分析角度出发,难以对大扰动场景下的RoCoF与频率最低点等安全指标进行衡量。同时,也未能充分考虑虚拟惯量优化配置对系统运行经济性造成的影响。
5 惯量相关问题未来展望高占比可再生能源与电力电子设备的渗透导致电力系统惯量支撑与频率调节能力遭到削弱,而惯量在频率安全中发挥着不可或缺的作用。因此,针对新型电力系统等效惯量评估、需求及优化面临的挑战以及存在的不足,本文尝试探讨未来潜在的研究方向:
(1) 研究基于变流器接口单体设备层面的实时在线等效惯量评估方法
基于变流器接口资源的高比例渗透是导致新型电力系统难以准确获取等效惯量的主要原因。变流器单体设备对外表现出的等效惯量支撑特性与其控制方法、结构参数、运行状态密切相关。基于参数辨识理论结合转子运动方程的等效惯量评估方法默认变流器并网控制策略及参数均是已知的,但设备参数及控制策略在实际工程中很大概率无法全面获取。因此,可考虑合适的扰动类型结合人工智能方法对变流器单体设备层面进行连续实时的等效惯量评估,降低对变流器单体设备运行控制及状态参数的依赖。
(2) 研究面向频率响应分区的系统临界惯量需求及在线惯量评估方法
非同步机电源高比例渗透导致系统频率响应空间特性愈加明显。已有成果将系统等效处理成一个孤立的整体,而实际电网属于互联系统,忽略了联络线功率变化对系统频率的影响,导致该方式不能具有针对性地考虑局部可再生能源高渗透系统的真实临界惯量需求,从而造成获取的系统整体临界惯量需求不准确。因此,可根据系统频率响应特性对系统进行分区处理,计及多类型影响惯量需求与惯量评估的因素开展在线分区惯量估计及需求量化评估方法。
(3) 研究面向分区频率安全约束的等效惯量优化方法
新型电力系统内部各子区频率响应特性各异,导致各子区对频率安全的要求也具有特异性,比如新能源占比较高的子区对频率要求进一步提高。因此将系统频率安全约束视作全局量或统一量,并采用“平均化”的思想对待整个系统,将难以满足各子区差异化的频率安全需求。为满足系统中变流器电源高渗透子区系统严格的频率安全要求。因此,有必要开展面向频率安全差异性约束的系统优化方法,以充分协调系统内转动惯量与虚拟惯量。
(4) 研究基于源-网-荷-储协同的等效惯量定量补偿控制方法
在惯量资源日渐紧缺的情况下,需考虑在控制层面如何弥补惯量需求与等效惯量之间的缺额,源-网-荷-储多类型惯量资源的定量协同需要明确各自所提供等效惯量的动态变化特性。然而,目前基于变流器的非同步机电源在提供等效惯量支撑方面主要聚焦提升设备自身的惯量支撑能力,较少涉及多类型惯量资源之间的定量协同。为了充分发挥各部分等效惯量的支撑作用,因此,有必要开展基于源-网-荷-储协同的等效惯量定量补偿控制方法,以更好地满足系统临界惯量需求。
6 结论高比例的可再生能源通过电力电子设备涉网极大地削弱了系统的惯量支撑能力,导致电力系统“低惯量”特征愈加明显。准确评估系统的等效惯量水平,精准量化系统的惯量需求以及合理优化系统的惯量配置对于电网调度运行人员有效应对各种复杂低惯量运行场景问题至关重要。本文首先诠释了系统等效惯量的概念与组成。根据电源同步方式及扰动类型归类等效惯量评估方法以准确感知设备及系统的等效惯量支撑能力。本文具体结论如下:
1)从能量连续变化角度诠释了系统等效惯量的概念及其组成,明确了系统等效惯量的时变特性主要受电流源型虚拟惯量的影响。
2)根据电源同步方式及扰动类型归类了等效惯量评估方法以准确感知设备及系统的等效惯量支撑能力,总结了基于不同扰动类型评估方法的优缺点及适应场景。为准确刻画等效惯量的时变特性,明确了深入研究非同步机电源等效惯量动态支撑特性研究的必要性。
3)为了切实提升系统频率运行安全性,从惯量需求、惯量优化运行两方面对低惯量电力系统的研究路径及现状进行了归纳,分析了在频率响应空间特性愈加明显的场景下,满足系统惯量需求及进行惯量优化的必要性。
4)聚焦新型电力系统的特点及研究现状存在的不足,从非同步机电源在线等效惯量评估、分区惯量需求评估及优化、多类型惯量资源定量协同四个方面进行了展望,以期为解决新型电力系统中的低惯量问题提供参考。
| [1] |
SAJADI A, KENYON R W, HODGE B M. Synchronization in electric power networks with inherent heterogeneity up to 100% inverter-based renewable generation[J]. Nature Communications, 2022, 13(1): 2490. DOI:10.1038/s41467-022-30164-3 (  0) 0) |
| [2] |
GU Y J, GREEN T C. Power system stability with a high penetration of inverter-based resources[J]. Proceedings of the IEEE, 2023, 111(7): 832-853. DOI:10.1109/JPROC.2022.3179826 (  0) 0) |
| [3] |
孙华东, 王宝财, 李文锋, 等. 高比例电力电子电力系统频率响应的惯量体系研究[J]. 中国电机工程学报, 2020, 40(16): 5179-5191. SUN Huadong, WANG Baocai, LI Wenfeng, et al. Research on inertia system of frequency response for power system with high penetration electronics[J]. Proceedings of the CSEE, 2020, 40(16): 5179-5191. (  0) 0) |
| [4] |
ENTSO-E. The inertia challenge in Europe–Present and long-term perspective[R]. Brussels, Belgium: ENTSO-E, 2020.
(  0) 0) |
| [5] |
鲁宗相, 姜继恒, 乔颖, 等. 新型电力系统广义惯量分析与优化研究综述[J]. 中国电机工程学报, 2023, 43(5): 1754-1775. LU Zongxiang, JIANG Jiheng, QIAO Ying, et al. A review on generalized inertia analysis and optimization of new power systems[J]. Proceedings of the CSEE, 2023, 43(5): 1754-1775. (  0) 0) |
| [6] |
朱介北, 罗贺予, 俞露杰, 等. 新型电力系统惯量-频率"云-网-端"感知与控制技术展望[J]. 高电压技术, 2024, 50(7): 3090-3104. ZHU Jiebei, LUO Heyu, YU Lujie, et al. Modern power system inertia-frequency sensing and control technology outlook across "Cloud-Grid-Terminal"[J]. High Voltage Engineering, 2024, 50(7): 3090-3104. DOI:10.13336/j.1003-6520.hve.20240200 (  0) 0) |
| [7] |
张祥宇, 金召展, 付媛, 等. 基于频率变化极值时间的风电虚拟惯量约束与支撑控制[J]. 高电压技术, 2023, 49(6): 2491-2504. ZHANG Xiangyu, JIN Zhaozhan, FU Yuan, et al. Virtual inertia constrain and support control of wind turbines based on variable frequency limit time[J]. High Voltage Engineering, 2023, 49(6): 2491-2504. DOI:10.13336/j.1003-6520.hve.20221394 (  0) 0) |
| [8] |
李国庆, 刘先超, 辛业春, 等. 含高比例新能源的电力系统频率稳定研究综述[J]. 高电压技术, 2024, 50(3): 1165-1181. LI Guoqing, LIU Xianchao, XIN Yechun, et al. Research on frequency stability of power system with high penetration renewable energy: a review[J]. High Voltage Engineering, 2024, 50(3): 1165-1181. DOI:10.13336/j.1003-6520.hve.20232053 (  0) 0) |
| [9] |
黄萌, 凌扬坚, 耿华, 等. 功率同步控制的构网型变流器多机交互分析与稳定控制研究综述[J]. 高电压技术, 2023, 49(11): 4571-4583. HUANG Meng, LING Yangjian, GENG Hua, et al. An overview on multi-VSCs interaction analysis and stability controls of grid-forming converters with power synchronization control[J]. High Voltage Engineering, 2023, 49(11): 4571-4583. DOI:10.13336/j.1003-6520.hve.20230748 (  0) 0) |
| [10] |
DHARA P K, RATHER Z H. Non-synchronous inertia estimation in a renewable energy integrated power system with reduced number of monitoring nodes[J]. IEEE Transactions on Sustainable Energy, 2023, 14(2): 864-875. DOI:10.1109/TSTE.2022.3227603 (  0) 0) |
| [11] |
ZAKER B, GHAREHPETIAN G B, KARRARI M, et al. Simultaneous parameter identification of synchronous generator and excitation system using online measurements[J]. IEEE Transactions on Smart Grid, 2016, 7(3): 1230-1238. DOI:10.1109/TSG.2015.2478971 (  0) 0) |
| [12] |
ARASTOU A, RABIEYAN H, KARRARI M. A novel pss-based online test procedure for parameter estimation of synchronous generator using the governor system[J]. IEEE Transactions on Energy Conversion, 2021, 36(4): 3178-3187. DOI:10.1109/TEC.2021.3066480 (  0) 0) |
| [13] |
HUANG Z Y, DU P W, KOSTEREV D, et al. Generator dynamic model validation and parameter calibration using phasor measurements at the point of connection[J]. IEEE Transactions on Power Systems, 2013, 28(2): 1939-1949. DOI:10.1109/TPWRS.2013.2251482 (  0) 0) |
| [14] |
MITRA A, MOHAPATRA A, CHAKRABARTI S, et al. Online measurement based joint parameter estimation of synchronous generator and exciter[J]. IEEE Transactions on Energy Conversion, 2021, 36(2): 820-830. DOI:10.1109/TEC.2020.3034733 (  0) 0) |
| [15] |
TAN B D, ZHAO J B, TERZIJA V, et al. Decentralized data-driven estimation of generator rotor speed and inertia constant based on adaptive unscented Kalman filter[J]. International Journal of Electrical Power & Energy Systems, 2022, 137: 107853. (  0) 0) |
| [16] |
杨德友, 邵致远, 王博. 基于动态模式分解的发电机惯量及阻尼系数评估方法[J]. 电网技术, 2022, 46(1): 311-319. YANG Deyou, SHAO Zhiyuan, WANG Bo. Evaluation of generator inertia and damping coefficient based on dynamic mode decomposition[J]. Power System Technology, 2022, 46(1): 311-319. (  0) 0) |
| [17] |
李生虎, 朱争高, 齐楠, 等. 计及调速/励磁系统的同步发电机等效惯量辨识[J]. 电力系统及其自动化学报, 2023, 35(10): 18-25. LI Shenghu, ZHU Zhengggao, QI Nan, et al. Identification of equivalent inertia of SG with governor and excitation systems[J]. Proceedings of the CSU-EPSA, 2023, 35(10): 18-25. (  0) 0) |
| [18] |
陈湘, 付强, 宾子君, 等. 附加频率控制下并网换流器的动态惯量及其量化评估[J]. 电力系统自动化, 2024, 48(8): 131-140. CHEN Xiang, FU Qiang, BIN Zijun, et al. Dynamic inertia of grid-connected converter with additional frequency control and its quantitative evaluation[J]. Automation of Electric Power Systems, 2024, 48(8): 131-140. (  0) 0) |
| [19] |
李昭良, 胥国毅, 王程, 等. 计及功率响应延时补偿的换流器接口电源等效惯量估计方法[J]. 电力系统自动化, 2023, 47(1): 12-21. LI Zhaoliang, XU Guoyi, WANG Cheng, et al. Equivalent inertia estimation method for converter-interfaced generator considering power response delay compensation[J]. Automation of Electric Power Systems, 2023, 47(1): 12-21. (  0) 0) |
| [20] |
朱介北, 朱学科, 陈彬彬, 等. 基于延时补偿的新能源惯性时间常数评估方法[J]. 电力系统自动化, 2024, 48(8): 101-110. ZHU Jiebei, ZHU Xueke, CHEN Binbin, et al. Evaluation method for inertial time constant of renewable energy based on delay compensation[J]. Automation of Electric Power Systems, 2024, 48(8): 101-110. (  0) 0) |
| [21] |
李玉京, 胡鹏飞, 曹宇, 等. 计及频率响应延时的构网型变流器惯量参数数据驱动估计方法[J]. 电力系统自动化, 2024, 48(19): 80-88. LI Yujing, HU Pengfei, CAO Yu, et al. Data-driven estimation method for inertia parameters of grid-forming converter considering frequency response delay[J]. Automation of Electric Power Systems, 2024, 48(19): 80-88. (  0) 0) |
| [22] |
TAN B D, ZHAO J B. Data-driven time-varying inertia estimation of inverter-based resources[J]. IEEE Transactions on Power Systems, 2023, 38(2): 1795-1798. DOI:10.1109/TPWRS.2022.3229869 (  0) 0) |
| [23] |
LIU K, XU Y J, GU W, et al. A bayesian approach for online inertia estimation of synchronous and nonsynchronous generators[J]. IEEE Transactions on Instrumentation and Measurement, 2024, 73: 1006012. (  0) 0) |
| [24] |
SUN L, ZHAO X W. Impacts of phase-locked loop and reactive power control on inertia provision by DFIG wind turbine[J]. IEEE Transactions on Energy Conversion, 2022, 37(1): 109-119. DOI:10.1109/TEC.2021.3100685 (  0) 0) |
| [25] |
刘皓明, 任秋业, 张占奎, 等. 双馈风机等效惯性时间常数计算及转差率反馈惯量控制策略[J]. 电力系统自动化, 2018, 42(17): 49-57. LIU Haoming, REN Qiuye, ZHANG Zhankui, et al. Calculation of equivalent inertia time constant for doubly-fed induction generators and slip-feedback inertia control strategy[J]. Automation of Electric Power Systems, 2018, 42(17): 49-57. DOI:10.7500/AEPS20171009001 (  0) 0) |
| [26] |
王彤, 邢其鹏, 李鸿恩, 等. 计及虚拟惯量控制的DFIG等效惯量在线评估与响应特性分析[J]. 电力系统保护与控制, 2022, 50(11): 52-60. WANG Tong, XING Qipeng, LI Hong'en, et al. Online evaluation and response characteristics analysis of equivalent inertia of a doubly-fed induction generator incorporating virtual inertia control[J]. Power System Protection and Control, 2022, 50(11): 52-60. (  0) 0) |
| [27] |
GUO X, ZHU D H, ZOU X D, et al. Dynamic inertia evaluation for type-3 wind turbines based on inertia function[J]. IEEE Journal on Emerging and Selected Topics in Circuits and Systems, 2021, 11(1): 28-38. DOI:10.1109/JETCAS.2021.3051029 (  0) 0) |
| [28] |
李世春, 徐松林, 李惠子, 等. 风电场等效虚拟惯量快速估计方法[J]. 电网技术, 2021, 45(12): 4683-4691. LI Shichun, XU Songlin, LI Huizi, et al. Rapid estimation of equivalent virtual inertia of wind farm[J]. Power System Technology, 2021, 45(12): 4683-4691. (  0) 0) |
| [29] |
安军, 盛帅, 周毅博, 等. 基于量测数据的风电场等效虚拟惯量评估方法[J]. 电网技术, 2023, 47(5): 1819-1827. AN Jun, SHENG Shuai, ZHOU Yibo, et al. Evaluation of equivalent virtual inertia of wind farm based on measured data[J]. Power System Technology, 2023, 47(5): 1819-1827. (  0) 0) |
| [30] |
巴文岚, 文云峰, 叶希, 等. 风电高渗透电网等效惯量概率预测方法[J]. 电力自动化设备, 2023, 43(3): 124-130, 165. BA Wenlan, WEN Yunfeng, YE Xi, et al. Probability prediction method of equivalent inertia for high wind power penetration grid[J]. Electric Power Automation Equipment, 2023, 43(3): 124-130, 165. (  0) 0) |
| [31] |
韩帅, 张峰, 丁磊, 等. 基于混合Copula函数的风电场可用惯量评估方法[J]. 电力自动化设备, 2021, 41(3): 189-195, 210. HAN Shuai, ZHANG Feng, DING Lei, et al. Available inertia evaluation method of wind farm based on mixed Copula function[J]. Electric Power Automation Equipment, 2021, 41(3): 189-195, 210. (  0) 0) |
| [32] |
李东东, 张先明, 姚寅, 等. 计及转子动能损失和风速相关性的风电场有效惯量估计[J]. 电力系统保护与控制, 2023, 51(22): 63-73. LI Dongdong, ZHANG Xianming, YAO Yin, et al. Estimation of effective inertia of a wind farm considering rotor kinetic energy loss and wind velocity correlation[J]. Power System Protection and Control, 2023, 51(22): 63-73. (  0) 0) |
| [33] |
CHEN P W, QI C C, CHEN X. Virtual inertia estimation method of DFIG-based wind farm with additional frequency control[J]. Journal of Modern Power Systems and Clean Energy, 2021, 9(5): 1076-1087. DOI:10.35833/MPCE.2020.000908 (  0) 0) |
| [34] |
胡安平, 杨波, 潘鹏鹏, 等. 基于电力电子接口的储能系统惯性特征研究[J]. 中国电机工程学报, 2018, 38(17): 4999-5008. HU Anping, YANG Bo, PAN Pengpeng, et al. Study on inertial characteristics of energy storage system with power electronic interface[J]. Proceedings of the CSEE, 2018, 38(17): 4999-5008. (  0) 0) |
| [35] |
李世春, 邓蕊, 薛臻瑶, 等. 基于虚拟惯量计算的储能虚拟惯量补偿控制方法[J]. 电力系统及其自动化学报, 2023, 35(11): 114-121. LI Shichun, DANG Rui, XUE Zhenyao, et al. Virtual inertia compensation control method for energy storage device based on calculation of virtual inertia[J]. Proceedings of the CSU-EPSA, 2023, 35(11): 114-121. (  0) 0) |
| [36] |
李世春, 张业丽, 刘颂凯, 等. 跟网型电化学储能虚拟惯性常数的常数化计算方法[J]. 电力系统自动化, 2024, 48(20): 149-158. LI Shichun, ZHANG Yeli, LIU Songkai, et al. Constantized calculation method of virtual inertia constant for grid-following electrochemical energy storage[J]. Automation of Electric Power Systems, 2024, 48(20): 149-158. DOI:10.7500/AEPS20240108002 (  0) 0) |
| [37] |
刘方蕾, 胥国毅, 王凡, 等. 基于差值计算法的系统分区惯量评估方法[J]. 电力系统自动化, 2020, 44(20): 46-53. LIU Fanglei, XU Guoyi, WANG Fan, et al. Assessment method of system partition inertia based on differential calculation method[J]. Automation of Electric Power Systems, 2020, 44(20): 46-53. (  0) 0) |
| [38] |
BEST R J, BROGAN P V, MORROW D J. Power system inertia estimation using HVDC power perturbations[J]. IEEE Transactions on Power Systems, 2021, 36(3): 1890-1899. DOI:10.1109/TPWRS.2020.3028614 (  0) 0) |
| [39] |
马燕峰, 李金媛, 王子建, 等. 基于量测数据的新能源电力系统区域等效惯量评估方法[J]. 电工技术学报, 2024, 39(17): 5406-5421. MA Yanfeng, LI Jinyuan, WANG Zijian, et al. Assessment method of regional equivalent inertia of new energy power system based on measured data[J]. Transactions of China Electrotechnical Society, 2024, 39(17): 5406-5421. (  0) 0) |
| [40] |
SHAMS N, WALL P, TERZIJA V. Active power imbalance detection, size and location estimation using limited PMU measurements[J]. IEEE Transactions on Power Systems, 2019, 34(2): 1362-1372. DOI:10.1109/TPWRS.2018.2872868 (  0) 0) |
| [41] |
AZIZIPANAH-ABARGHOOEE R, MALEKPOUR M, PAOLONE M, et al. A new approach to the online estimation of the loss of generation size in power systems[J]. IEEE Transactions on Power Systems, 2019, 34(3): 2103-2113. DOI:10.1109/TPWRS.2018.2879542 (  0) 0) |
| [42] |
ZOGRAFOS D, GHANDHARI M, ERIKSSON R. Power system inertia estimation: utilization of frequency and voltage response after a disturbance[J]. Electric Power Systems Research, 2018, 161: 52-60. DOI:10.1016/j.epsr.2018.04.008 (  0) 0) |
| [43] |
贾焦心, 杨添淇, 颜湘武, 等. 电力电子并网装备等效惯量评估研究进展[J]. 电力自动化设备, 2023, 43(9): 3-10. JIA Jiaoxin, YANG Tianqi, YAN Xiangwu, et al. Research progress on equivalent inertia estimation of grid-connected power electronic devices[J]. Electric Power Automation Equipment, 2023, 43(9): 3-10. (  0) 0) |
| [44] |
ASHTON P M, SAUNDERS C S, TAYLOR G A, et al. Inertia estimation of the GB power system using synchrophasor measurements[J]. IEEE Transactions on Power Systems, 2015, 30(2): 701-709. DOI:10.1109/TPWRS.2014.2333776 (  0) 0) |
| [45] |
WANG W K, YAO W X, CHEN C, et al. Fast and accurate frequency response estimation for large power system disturbances using second derivative of frequency data[J]. IEEE Transactions on Power Systems, 2020, 35(3): 2483-2486. DOI:10.1109/TPWRS.2020.2977504 (  0) 0) |
| [46] |
YIN H, WU Y R, QIU W, et al. Precise ROCOF estimation algorithm for low inertia power grids[J]. Electric Power Systems Research, 2022, 209: 107968. DOI:10.1016/j.epsr.2022.107968 (  0) 0) |
| [47] |
PHURAILATPAM C, RATHER Z H, BAHRANI B, et al. Measurement-based estimation of inertia in AC microgrids[J]. IEEE Transactions on Sustainable Energy, 2020, 11(3): 1975-1984. DOI:10.1109/TSTE.2019.2948224 (  0) 0) |
| [48] |
裴铭, 叶林, 罗雅迪, 等. 计及频率响应时空相关性的新能源电力系统惯量估计方法[J]. 电力系统自动化, 2024, 48(8): 53-66. PEI Ming, YE Lin, LUO Yadi, et al. Inertia estimation method for power system with renewable energy considering spatio-temporal correlation of frequency response[J]. Automation of Electric Power Systems, 2024, 48(8): 53-66. (  0) 0) |
| [49] |
MILANO F, ORTEGA Á. Frequency divider[J]. IEEE Transactions on Power Systems, 2017, 32(2): 1493-1501. DOI:10.1109/TPEL.2016.2543222 (  0) 0) |
| [50] |
MILANO F, ORTEGA Á. A method for evaluating frequency regulation in an electrical grid–Part I: theory[J]. IEEE Transactions on Power Systems, 2021, 36(1): 183-193. DOI:10.1109/TPWRS.2020.3007847 (  0) 0) |
| [51] |
ORTEGA Á, MILANO F. A method for evaluating frequency regulation in an electrical grid–Part II: applications to non-synchronous devices[J]. IEEE Transactions on Power Systems, 2021, 36(1): 194-203. DOI:10.1109/TPWRS.2020.3007851 (  0) 0) |
| [52] |
LIU M Y, CHEN J R, MILANO F. On-line inertia estimation for synchronous and non-synchronous devices[J]. IEEE Transactions on Power Systems, 2021, 36(3): 2693-2701. DOI:10.1109/TPWRS.2020.3037265 (  0) 0) |
| [53] |
刘方蕾, 胥国毅, 刘家豪, 等. 考虑电网结构和参数的电力系统惯量分布特性[J]. 电力系统自动化, 2021, 45(23): 60-67. LIU Fanglei, XU Guoyi, LIU Jiahao, et al. Inertia distribution characteristics of power system considering structure and parameters of power grid[J]. Automation of Electric Power Systems, 2021, 45(23): 60-67. (  0) 0) |
| [54] |
刘家豪, 王程, 毕天姝. 面向新能源电力系统频率时空动态的节点等效惯量指标及其应用[J]. 中国电机工程学报, 2023, 43(20): 7773-7788. LIU Jiahao, WANG Cheng, BI Tianshu. Node equivalent inertia index for temporal-spatial frequency dynamics of renewable energy power system and its applications[J]. Proceedings of the CSEE, 2023, 43(20): 7773-7788. (  0) 0) |
| [55] |
李卫东, 丁奇力. 大扰动下电力系统惯性时空分布特性的表征形式初探[J]. 中国电机工程学报, 2024, 44(12): 4601-4614. LI Weidong, DING Qili. A preliminary research on the representation form of spatial-temporal distribution characteristics of power system inertia under large disturbances[J]. Proceedings of the CSEE, 2024, 44(12): 4601-4614. (  0) 0) |
| [56] |
朱介北, 郭力源, 王伟, 等. 基于二阶罚函数自适应变阶拟合的全局电网惯量时空感知[J]. 电力系统自动化, 2024, 48(19): 69-79. ZHU Jiebei, GUO Liyuan, WANG Wei, et al. Temporal-spatio inertia perception of global power grid based on adaptive variable-order fitting of second-order penalty function[J]. Automation of Electric Power Systems, 2024, 48(19): 69-79. (  0) 0) |
| [57] |
刘勃, 陈中, 王毅, 等. 基于斜坡渐变扰动的新型电力系统等效惯量评估[J]. 电力自动化设备, 2024, 44(3): 49-56. LIU Bo, CHEN Zhong, WANG Yi, et al. Ramp gradient disturbance based equivalent inertia estimation of new type power system[J]. Electric Power Automation Equipment, 2024, 44(3): 49-56. (  0) 0) |
| [58] |
SFETKOS A I, KONTIS E O, PAPADOPOULOS T A, et al. Inertia estimation of multi-area power systems using tie-line measurements and modal sensitivity analysis[J]. Electric Power Systems Research, 2023, 224: 109642. DOI:10.1016/j.epsr.2023.1096421 (  0) 0) |
| [59] |
WANG B, YANG D Y, CAI G W, et al. An improved electromechanical oscillation-based inertia estimation method[J]. IEEE Transactions on Power Systems, 2022, 37(3): 2479-2482. DOI:10.1109/TPWRS.2022.3156441 (  0) 0) |
| [60] |
YANG D Y, WANG B, CAI G W, et al. Data-driven estimation of inertia for multiarea interconnected power systems using dynamic mode decomposition[J]. IEEE Transactions on Industrial Informatics, 2021, 17(4): 2686-2695. DOI:10.1109/TII.2020.2998074 (  0) 0) |
| [61] |
PANDA R K, MOHAPATRA A, SRIVASTAVA S C. Online estimation of system inertia in a power network utilizing synchrophasor measurements[J]. IEEE Transactions on Power Systems, 2020, 35(4): 3122-3132. DOI:10.1109/TPWRS.2019.2958603 (  0) 0) |
| [62] |
ZHANG J B, XU H C. Online identification of power system equivalent inertia constant[J]. IEEE Transactions on Industrial Electronics, 2017, 64(10): 8098-8107. DOI:10.1109/TIE.2017.2698414 (  0) 0) |
| [63] |
李元臣, 文云峰, 叶希, 等. 基于多新息辨识的电力系统节点惯量估计方法[J]. 电力自动化设备, 2022, 42(8): 89-95. LI Yuanchen, WEN Yunfeng, YE Xi, et al. Estimation method of power system nodal inertia based on multi-innovation identification[J]. Electric Power Automation Equipment, 2022, 42(8): 89-95. (  0) 0) |
| [64] |
李勇, 常樊睿, 彭衍建, 等. 基于小扰动频率量测数据的电网节点惯量分布评估方法[J]. 电力系统自动化, 2024, 48(13): 50-59. LI Yong, CHANG Fanrui, PENG Yanjian, et al. Evaluation method for node inertia distribution of power grids based on small disturbance frequency measurement data[J]. Automation of Electric Power Systems, 2024, 48(13): 50-59. DOI:10.7500/AEPS20230814004 (  0) 0) |
| [65] |
ZHANG W Q, WEN Y F, CHUNG C Y. Impedance-based online estimation of nodal inertia and primary frequency regulation capability[J]. IEEE Transactions on Power Systems, 2023, 38(3): 2748-2760. DOI:10.1109/TPWRS.2022.3186525 (  0) 0) |
| [66] |
PRASAD R, PADHY N P. Spatiotemporal pattern analysis of nodal inertia using convex combination of walks of generator nodes in varying inertia system[J]. IEEE Transactions on Power Systems, 2023, 38(5): 4476-4488. DOI:10.1109/TPWRS.2022.3213419 (  0) 0) |
| [67] |
黄思维, 张俊勃, 曾繁宏. 适用于电力系统惯性秒级追踪的高效在线算法[J]. 高电压技术, 2021, 47(10): 3519-3527. HUANG Siwei, ZHANG Junbo, ZENG Fanhong. Efficient online algorithm for fast inertia tracking of power system[J]. High Voltage Engineering, 2021, 47(10): 3519-3527. DOI:10.13336/j.1003-6520.hve.20210774 (  0) 0) |
| [68] |
KERDPHOL T, WATANABE M, NISHIKAWA R, et al. Inertia estimation of the 60 Hz Japanese power system from synchrophasor measurements[J]. IEEE Transactions on Power Systems, 2023, 38(1): 753-766. DOI:10.1109/TPWRS.2022.3168037 (  0) 0) |
| [69] |
刘巨, 赵红生, 李梦颖, 等. 基于功率谱密度分析的新能源电力系统等效惯量评估[J]. 高电压技术, 2022, 48(1): 178-188. LIU Ju, ZHAO Hongsheng, LI Mengying, et al. An equivalent inertia evaluation method of power system based on power spectral density analysis[J]. High Voltage Engineering, 2022, 48(1): 178-188. DOI:10.13336/j.1003-6520.hve.20210774 (  0) 0) |
| [70] |
BIZZARRI F, DEL GIUDICE D, GRILLO S, et al. Inertia estimation through covariance matrix[J]. IEEE Transactions on Power Systems, 2024, 39(1): 947-956. DOI:10.1109/TPWRS.2023.3236059 (  0) 0) |
| [71] |
GOTTI D, BIZZARRI F, BRAMBILLA A, et al. Inertia estimation of a power system area based on iterative equation error system identification[J]. IEEE Transactions on Power Systems, 2024, 39(5): 6469-6481. DOI:10.1109/TPWRS.2024.3353077 (  0) 0) |
| [72] |
李世春, 宋秋爽, 薛臻瑶, 等. 含风电虚拟惯性响应的新能源电力系统惯量估计[J]. 电力工程技术, 2023, 42(2): 84-93. LI Shichun, SONG Qiushuang, XUE Zhenyao, et al. Inertia estimation of new energy power system with virtual inertia response of wind power[J]. Electric Power Engineering Technology, 2023, 42(2): 84-93. (  0) 0) |
| [73] |
GOTTI D, LEDESMA P, AMARIS H. A recursive system identification inertia estimator for traditional and converter-interfaced generators[J]. International Journal of Electrical Power & Energy Systems, 2023, 154: 109445. (  0) 0) |
| [74] |
SCHIFFER J, ARISTIDOU P, ORTEGA R. Online estimation of power system inertia using dynamic regressor extension and mixing[J]. IEEE Transactions on Power Systems, 2019, 34(6): 4993-5001. DOI:10.1109/TPWRS.2019.2915249 (  0) 0) |
| [75] |
LINARO D, BIZZARRI F, DEL GIUDICE D, et al. Continuous estimation of power system inertia using convolutional neural networks[J]. Nature Communications, 2023, 14(1): 4440. DOI:10.1038/s41467-023-40192-2 (  0) 0) |
| [76] |
GUO J P, WANG X Z, OOI B T. Estimation of inertia for synchronous and non-synchronous generators based on ambient measurements[J]. IEEE Transactions on Power Systems, 2022, 37(5): 3747-3757. DOI:10.1109/TPWRS.2021.3134818 (  0) 0) |
| [77] |
MAZIDI M, MCKELVEY T, CHEN P Y. A pure data-driven method for online inertia estimation in power systems using local rational model approach[J]. IEEE Transactions on Industry Applications, 2023, 59(5): 5506-5516. DOI:10.1109/TIA.2023.3288503 (  0) 0) |
| [78] |
BI T S, LIU J H, WANG C. Online estimation of area-level inertia considering inter-area equivalent frequency dynamics[J]. IEEE Transactions on Power Systems, 2025, 40(1): 57-72. DOI:10.1109/TPWRS.2024.3402269 (  0) 0) |
| [79] |
LIU J H, WANG C, BI T S, et al. Online estimation of POI-level aggregated inertia considering frequency spatial correlation[J]. IEEE Transactions on Power Systems, 2023, 38(4): 3232-3244. (  0) 0) |
| [80] |
ZENG F H, ZHANG J B, ZHOU Y, et al. Online identification of inertia distribution in normal operating power system[J]. IEEE Transactions on Power Systems, 2020, 35(4): 3301-3304. DOI:10.1109/TPWRS.2020.2986721 (  0) 0) |
| [81] |
文云峰, 张武其, 郭威. 电力系统惯量需求: 概念、指标及评估方法[J]. 电力系统自动化, 2024, 48(8): 30-41. WEN Yunfeng, ZHANG Wuqi, GUO Wei. Inertia requirement of power system: concepts, indexes, and evaluation method[J]. Automation of Electric Power Systems, 2024, 48(8): 30-41. (  0) 0) |
| [82] |
刘其泳, 于之虹, 张璐路, 等. 基于惯量比的电网频率支撑能力在线评估方法[J]. 电网技术, 2023, 47(2): 493-501. LIU Qiyong, YU Zhihong, ZHANG Lulu, et al. Online frequency support capacity assessment of power grid based on inertia ratio[J]. Power System Technology, 2023, 47(2): 493-501. (  0) 0) |
| [83] |
EIRGRID. Enduring connection policy 1 constraints report for area B solar and wind[R]. Dublin, Ireland: EIRGRID, 2020.
(  0) 0) |
| [84] |
国家能源局. 电力系统惯量支撑和一次调频能力技术要求: DL/T 2669—2023[S]. 北京: 中国电力出版社, 2023. National Energy Administration. Technical requirements for power system inertia support and primary frequency control: DL/T 2669—2023[S]. Beijing, China: China Electric Power Press, 2023. (  0) 0) |
| [85] |
林晓煌, 文云峰, 杨伟峰. 惯量安全域: 概念、特点及评估方法[J]. 中国电机工程学报, 2021, 41(9): 3065-3078. LIN Xiaohuang, WEN Yunfeng, YANG Weifeng. Inertia security region: concept, characteristics, and assessment method[J]. Proceedings of the CSEE, 2021, 41(9): 3065-3078. (  0) 0) |
| [86] |
JOHNSON S C, PAPAGEORGIOU D J, MALLAPRAGADA D S, et al. Evaluating rotational inertia as a component of grid reliability with high penetrations of variable renewable energy[J]. Energy, 2019, 180: 258-271. DOI:10.1016/j.energy.2019.04.216 (  0) 0) |
| [87] |
BONFIGLIO A, FRESIA M, MINETTI M, et al. Inertia requirements assessment for the Italian transmission network in the future network scenario[C]//2023 IEEE Belgrade PowerTech. Belgrade, Serbia: IEEE, 2023: 1-5.
(  0) 0) |
| [88] |
GU H J, YAN R F, SAHA T K. Minimum synchronous inertia requirement of renewable power systems[J]. IEEE Transactions on Power Systems, 2018, 33(2): 1533-1543. DOI:10.1109/TPWRS.2017.2720621 (  0) 0) |
| [89] |
AGATHOKLEOUS C, EHNBERG J. A quantitative study on the requirement for additional inertia in the European power system until 2050 and the potential role of wind power[J]. Energies, 2020, 13(9): 2309. DOI:10.3390/en13092309 (  0) 0) |
| [90] |
PEPICIELLO A, VACCARO A. An optimization-based method for estimating critical inertia in smart grids[C]//2019 IEEE International Conference on Systems, Man and Cybernetics (SMC). Bari, Italy: IEEE, 2019: 2237-2241.
(  0) 0) |
| [91] |
张祥宇, 朱永健, 付媛. 基于系统惯量需求的风储协同快速频率响应技术[J]. 中国电机工程学报, 2023, 43(14): 5415-5428. ZHANG Xiangyu, ZHU Yongjian, FU Yuan. Wind-storage cooperative fast frequency response technology based on system inertia demand[J]. Proceedings of the CSEE, 2023, 43(14): 5415-5428. (  0) 0) |
| [92] |
张祥宇, 胡剑峰, 付媛, 等. 风储联合系统的虚拟惯量需求与协同支撑[J]. 电工技术学报, 2024, 39(3): 672-685. ZHANG Xiangyu, HU Jianfeng, FU Yuan, et al. Virtual inertia demand and collaborative support of wind power and energy storage system[J]. Transactions of China Electrotechnical Society, 2024, 39(3): 672-685. (  0) 0) |
| [93] |
HU S L, YANG J Q, WANG Y, et al. Inertia and primary frequency response requirement assessment for high-penetration renewable power systems based on planning perspective[J]. Sustainability, 2023, 15(23): 16191. DOI:10.3390/su152316191 (  0) 0) |
| [94] |
RATNAM K S, PALANISAMY K, YANG G Y. Future low-inertia power systems: requirements, issues, and solutions-a review[J]. Renewable and Sustainable Energy Reviews, 2020, 124: 109773. DOI:10.1016/j.rser.2020.109773 (  0) 0) |
| [95] |
LIU B, DU P L. Virtual inertia and droop parameters quantitative determination method for VSC-HVDC in receiving-end area power systems with online inertia estimation based[J]. International Journal of Circuit Theory and Applications, 2024, 52(3): 1280-1301. DOI:10.1002/cta.3810 (  0) 0) |
| [96] |
FU A H, LEKIĆ A, KONTIS E O, et al. Impact of virtual synchronous generators on power system frequency dynamics[C]//2023 International Conference on Smart Energy Systems and Technologies (SEST). Mugla, Turkiye: IEEE, 2023: 1-6.
(  0) 0) |
| [97] |
李东东, 孙雅茹, 徐波, 等. 考虑频率稳定的新能源高渗透率电力系统最小惯量与一次调频容量评估方法[J]. 电力系统保护与控制, 2021, 49(23): 54-61. LI Dongdong, SUN Yaru, XU Bo, et al. Minimum inertia and primary frequency capacity assessment for a new energy high permeability power system considering frequency stability[J]. Power System Protection and Control, 2021, 49(23): 54-61. (  0) 0) |
| [98] |
WEN Y F, LI W Y, HUANG G, et al. Frequency dynamics constrained unit commitment with battery energy storage[J]. IEEE Transactions on Power Systems, 2016, 31(6): 5115-5125. DOI:10.1109/TPWRS.2016.2521882 (  0) 0) |
| [99] |
文云峰, 林晓煌. 孤岛与并网模式下微电网最低惯量需求评估[J]. 中国电机工程学报, 2021, 41(6): 2040-2052. WEN Yunfeng, LIN Xiaohuang. Minimum inertia requirement assessment of microgrids in islanded and grid-connected modes[J]. Proceedings of the CSEE, 2021, 41(6): 2040-2052. (  0) 0) |
| [100] |
GOLPIRA H, SEIFI H, MESSINA A R, et al. Maximum penetration level of micro-grids in large-scale power systems: frequency stability viewpoint[J]. IEEE Transactions on Power Systems, 2016, 31(6): 5163-5171. DOI:10.1109/TPWRS.2016.2538083 (  0) 0) |
| [101] |
GU H J, YAN R F, SAHA T. Review of system strength and inertia requirements for the national electricity market of Australia[J]. CSEE Journal of Power and Energy Systems, 2019, 5(3): 295-305. (  0) 0) |
| [102] |
王宝财, 孙华东, 李文锋, 等. 考虑动态频率约束的电力系统最小惯量评估[J]. 中国电机工程学报, 2022, 42(1): 114-126. WANG Baocai, SUN Huadong, LI Wenfeng, et al. Minimum inertia estimation of power system considering dynamic frequency constraints[J]. Proceedings of the CSEE, 2022, 42(1): 114-126. (  0) 0) |
| [103] |
LIU Z C, ZHOU T, CHEN Z, et al. Minimum inertia demand estimation of new power system considering diverse inertial resources based on deep neural network[J]. IET Energy Systems Integration, 2023, 5(1): 80-94. DOI:10.1049/esi2.12086 (  0) 0) |
| [104] |
王毅, 陈中, 周涛, 等. 计及新能源虚拟惯量的电力系统最低惯量评估[J]. 电气工程学报, 2024, 19(1): 254-260. WANG Yi, CHEN Zhong, ZHOU Tao, et al. Evaluation of minimum inertia of power system considering virtual inertia of renewable energy[J]. Journal of Electrical Engineering, 2024, 19(1): 254-260. (  0) 0) |
| [105] |
周涛, 刘子诚, 陈中, 等. 异步电机频率支撑能力分析及其等效惯量评估[J]. 电力工程技术, 2022, 41(4): 18-24, 107. ZHOU Tao, LIU Zicheng, CHEN Zhong, et al. Frequency support capacity of asynchronous motor and its equivalent inertia evaluation[J]. Electric Power Engineering Technology, 2022, 41(4): 18-24, 107. (  0) 0) |
| [106] |
周涛, 陈中, 王毅, 等. 计及异步电机频率响应的电力系统最低惯量评估[J]. 电力系统保护与控制, 2022, 50(20): 22-31. ZHOU Tao, CHEN Zhong, WANG Yi, et al. Evaluation of minimum inertia in power systems considering frequency response of induction machines[J]. Power System Protection and Control, 2022, 50(20): 22-31. (  0) 0) |
| [107] |
郭小龙, 杨桂兴, 张江飞, 等. 考虑时空特性与多指标约束的电力系统惯量需求评估[J]. 高电压技术, 2024, 50(1): 148-156. GUO Xiaolong, YANG Guixing, ZHANG Jiangfei, et al. Assessment of inertia demand in power system considering spatio-temporal characteristics and multi-index constraints[J]. High Voltage Engineering, 2024, 50(1): 148-156. DOI:10.13336/j.1003-6520.hve.20230189 (  0) 0) |
| [108] |
谢珍建, 汤奕. 计及源荷惯量特征的电力系统最小惯量需求评估[J]. 电力系统自动化, 2024, 48(10): 66-77. XIE Zhenjian, TANG Yi. Evaluation of minimum inertia requirement of power system considering source-load inertia characteristics[J]. Automation of Electric Power Systems, 2024, 48(10): 66-77. DOI:10.7500/AEPS20230826004 (  0) 0) |
| [109] |
张程铭, 柳璐, 程浩忠, 等. 考虑频率安全的电力系统规划与运行优化研究综述与展望[J]. 电网技术, 2022, 46(1): 250-264. ZHANG Chengming, LIU Lu, CHENG Haozhong, et al. Review and prospects of planning and operation optimization for electrical power systems considering frequency security[J]. Power System Technology, 2022, 46(1): 250-264. (  0) 0) |
| [110] |
王廷涛, 苗世洪, 姚福星, 等. 计及动态频率响应约束的高比例风电电力系统日前-日内联合调度策略[J]. 中国电机工程学报, 2024, 44(7): 2590-2603. WANG Tingtao, MIAO Shihong, YAO Fuxing, et al. Day-ahead and intra-day joint dispatch strategy of high proportion wind power system considering dynamic frequency response constraints[J]. Proceedings of the CSEE, 2024, 44(7): 2590-2603. (  0) 0) |
| [111] |
葛晓琳, 刘亚, 符杨, 等. 考虑惯量支撑及频率调节全过程的分布鲁棒机组组合[J]. 中国电机工程学报, 2021, 41(12): 4043-4057. GE Xiaolin, LIU Ya, FU Yang, et al. Distributed robust unit commitment considering the whole process of inertia support and frequency regulations[J]. Proceedings of the CSEE, 2021, 41(12): 4043-4057. (  0) 0) |
| [112] |
林恒先, 侯凯元, 陈磊, 等. 高比例风电电力系统考虑频率安全约束的机组组合[J]. 电网技术, 2021, 45(1): 1-9. LIN Hengxian, HOU Kaiyuan, CHEN Lei, et al. Unit commitment of power system with high proportion of wind power considering frequency safety constraints[J]. Power System Technology, 2021, 45(1): 1-9. (  0) 0) |
| [113] |
ZHANG Y Q, GUO Q L, ZHOU Y Z, et al. Frequency-constrained unit commitment for power systems with high renewable energy penetration[J]. International Journal of Electrical Power & Energy Systems, 2023, 153: 109274. (  0) 0) |
| [114] |
王博, 杨德友, 蔡国伟. 大规模风电并网条件下考虑动态频率约束的机组组合[J]. 电网技术, 2020, 44(7): 2513-2519. WANG Bo, YANG Deyou, CAI Guowei. Dynamic frequency constraint unit commitment in large-scale wind power grid connection[J]. Power System Technology, 2020, 44(7): 2513-2519. (  0) 0) |
| [115] |
江一航, 赵书强, 王慧, 等. 计及风电、调相机支撑特性的频率安全约束分布鲁棒机组组合调度方法[J]. 电工技术学报, 2025, 40(1): 80-95. JIANG Yihang, ZHAO Shuqiang, WANG Hui, et al. Distributionally robust frequency constrained unit commitment with frequency support of wind power and synchronous condenser[J]. Transactions of China Electrotechnical Society, 2025, 40(1): 80-95. (  0) 0) |
| [116] |
CHU Z D, MARKOVIC U, HUG G, et al. Towards optimal system scheduling with synthetic inertia provision from wind turbines[J]. IEEE Transactions on Power Systems, 2020, 35(5): 4056-4066. DOI:10.1109/TPWRS.2020.2985843 (  0) 0) |
| [117] |
李杨, 孙斌, 吴峰, 等. 考虑动态频率约束的多能源电力系统日前-日内优化调度[J]. 太阳能学报, 2024, 45(2): 406-415. LI Yang, SUN Bin, WU Feng, et al. Day-ahead and intra-day optimal scheduling of multi-energy power systems considering dynamic frequency constraints[J]. Acta Energiae Solaris Sinica, 2024, 45(2): 406-415. (  0) 0) |
| [118] |
ZHANG H Y, LIAO K, YANG J W, et al. Frequency-constrained expansion planning for wind and photovoltaic power in wind-photovoltaic-hydro-thermal multi-power system[J]. Applied Energy, 2024, 356: 122401. DOI:10.1016/j.apenergy.2023.122401 (  0) 0) |
| [119] |
叶畅, 柳丹, 杨欣宜, 等. 基于最小惯量评估的高比例新能源电力系统优化运行策略[J]. 电网技术, 2023, 47(2): 502-509. YE Chang, LIU Dan, YANG Xinyi, et al. Optimal operation strategy of high proportion new energy power system based on minimum inertia evaluation[J]. Power System Technology, 2023, 47(2): 502-509. (  0) 0) |
| [120] |
孙亮, 王伟镪, 王奕霏, 等. 计及最小惯量约束的风光火储联合系统优化调度[J]. 电力系统及其自动化学报, 2024, 36(8): 30-38. SUN Liang, WANG Weiqiang, WANG Yifei, et al. Optimal dispatching of wind-photovoltaic-thermal-storage combined system considering minimum inertia constraints[J]. Proceedings of the CSU-EPSA, 2024, 36(8): 30-38. (  0) 0) |
| [121] |
况理, 文云峰, 陆艺丹, 等. 含虚拟同步机的微电网频率稳定约束优化调度模型研究[J]. 中国电机工程学报, 2022, 42(1): 71-82. KUANG Li, WEN Yunfeng, LU Yidan, et al. Frequency stability constrained optimal dispatch model of microgrid with virtual synchronous machines[J]. Proceedings of the CSEE, 2022, 42(1): 71-82. (  0) 0) |
| [122] |
PATURET M, MARKOVIC U, DELIKARAOGLOU S, et al. Stochastic unit commitment in low-inertia grids[J]. IEEE Transactions on Power Systems, 2020, 35(5): 3448-3458. DOI:10.1109/TPWRS.2020.2987076 (  0) 0) |
| [123] |
WEN J X, BU S Q, LI F X, et al. Risk assessment and mitigation on area-level RoCoF for operational planning[J]. Energy, 2021, 228: 120632. DOI:10.1016/j.energy.2021.120632 (  0) 0) |
| [124] |
LI J M, QIAO Y, LU Z X, et al. Integrated frequency-constrained scheduling considering coordination of frequency regulation capabilities from multi-source converters[J]. Journal of Modern Power Systems and Clean Energy, 2024, 12(1): 261-274. DOI:10.35833/MPCE.2022.000717 (  0) 0) |
| [125] |
ZHANG C M, LIU L, CHENG H Z, et al. Frequency-constrained co-planning of generation and energy storage with high-penetration renewable energy[J]. Journal of Modern Power Systems and Clean Energy, 2021, 9(4): 760-775. DOI:10.35833/MPCE.2020.000743 (  0) 0) |
| [126] |
ZHANG Z, ZHOU M, WU Z Y, et al. A frequency security constrained scheduling approach considering wind farm providing frequency support and reserve[J]. IEEE Transactions on Sustainable Energy, 2022, 13(2): 1086-1100. DOI:10.1109/TSTE.2022.3150965 (  0) 0) |
| [127] |
GU H J, YAN R F, SAHA T K, et al. System strength and inertia constrained optimal generator dispatch under high renewable penetration[J]. IEEE Transactions on Sustainable Energy, 2020, 11(4): 2392-2406. DOI:10.1109/TSTE.2019.2957568 (  0) 0) |
| [128] |
LIU J H, WANG C, ZHAO J B, et al. RoCoF constrained unit commitment considering spatial difference in frequency dynamics[J]. IEEE Transactions on Power Systems, 2024, 39(1): 1111-1125. DOI:10.1109/TPWRS.2023.3240776 (  0) 0) |
| [129] |
LUO J Q, TENG F, BU S Q. Stability-constrained power system scheduling: a review[J]. IEEE Access, 2020, 8: 219331-219343. DOI:10.1109/ACCESS.2020.3042658 (  0) 0) |
| [130] |
POOLLA B K, BOLOGNANI S, DÖRFLER F. Optimal placement of virtual inertia in power grids[J]. IEEE Transactions on Automatic Control, 2017, 62(12): 6209-6220. DOI:10.1109/TAC.2017.2703302 (  0) 0) |
| [131] |
PAGNIER L, JACQUOD P. Optimal placement of inertia and primary control: a matrix perturbation theory approach[J]. IEEE Access, 2019, 7: 145889-145900. DOI:10.1109/ACCESS.2019.2945475 (  0) 0) |
| [132] |
POOLLA B K, GROß D, DÖRFLER F. Placement and implementation of grid-forming and grid-following virtual inertia and fast frequency response[J]. IEEE Transactions on Power Systems, 2019, 34(4): 3035-3046. DOI:10.1109/TPWRS.2019.2892290 (  0) 0) |
| [133] |
XIONG L Y, LI P H, WU F, et al. Stability enhancement of power systems with high DFIG-wind turbine penetration via virtual inertia planning[J]. IEEE Transactions on Power Systems, 2019, 34(2): 1352-1361. DOI:10.1109/TPWRS.2018.2869925 (  0) 0) |
| [134] |
GARCIA-ROSA P B, D'ARCO S, SUUL J A. Placement of virtual inertia from HVDC terminals based on a frequency deviation index[C]//2021 IEEE Madrid PowerTech. Madrid, Spain: IEEE, 2021: 1-7.
(  0) 0) |
| [135] |
刘瑞煦, 汪震, 吴佳良, 等. 考虑频率空间分布特性的虚拟惯量配置优化[J]. 电力系统自动化, 2024, 48(8): 122-130. LIU Ruixu, WANG Zhen, WU Jialiang, et al. Configuration optimization of virtual inertia considering spatial distribution characteristics of frequency[J]. Automation of Electric Power Systems, 2024, 48(8): 122-130. (  0) 0) |
| [136] |
朱兰, 仇念航, 张学涵. 计及节点惯量薄弱性评估的源网荷协调扩展规划[J/OL]. 现代电力, 1-16[2025-02-10]. https://doi.org/10.19725/j.cnki.1007-2322.2023.006. ZHU Lan, QIU Nianhang, ZHANG Xuehan. Generation-transmission-load coordinative expansion planning considering node inertia vulnerability assessment[J/OL]. Modern Electric Power, 1-16[2025-02-10]. https://doi.org/10.19725/j.cnki.1007-2322.2023.006. (  0) 0) |
| [137] |
张君黎, 徐政. 考虑RoCoF约束的新能源电力系统惯量分区配置方法[J]. 太阳能学报, 2023, 44(9): 18-28. ZHANG Junli, XU Zheng. Regional inertia configuration method of renewable energy power system considering RoCoF constraint[J]. Acta Energiae Solaris Sinica, 2023, 44(9): 18-28. (  0) 0) |
| [138] |
刘昊邦, 马辉, 熊致知. 基于Voronoi图重心内插法的虚拟惯量配置[J]. 电力系统自动化, 2020, 44(3): 66-73. LIU Haobang, MA Hui, XIONG Zhizhi. Virtual inertia configuration based on Voronoi diagram and center of gravity interpolation[J]. Automation of Electric Power Systems, 2020, 44(3): 66-73. (  0) 0) |
| [139] |
ZHU N X, HU P F, LI Y J, et al. Optimal allocation of energy storages: a perspective of system inertia support[J]. International Journal of Electrical Power & Energy Systems, 2023, 148: 108934. (  0) 0) |
| [140] |
王淋, 巨云涛, 吴文传, 等. 面向频率稳定提升的虚拟同步化微电网惯量阻尼参数优化设计[J]. 中国电机工程学报, 2021, 41(13): 4479-4489. WANG Lin, JU Yuntao, WU Wenchuan, et al. Optimal design of inertia and damping parameters of virtual synchronous microgrid for improving frequency stability[J]. Proceedings of the CSEE, 2021, 41(13): 4479-4489. (  0) 0) |
| [141] |
GOLPÎRA H, ATARODI A, AMINI S, et al. Optimal energy storage system-based virtual inertia placement: a frequency stability point of view[J]. IEEE Transactions on Power Systems, 2020, 35(6): 4824-4835. DOI:10.1109/TPWRS.2020.3000324 (  0) 0) |




 刘勃, 1993—,男,博士生, 主要从事低惯量系统运行、规划与控制的研究工作
刘勃, 1993—,男,博士生, 主要从事低惯量系统运行、规划与控制的研究工作