机构自由度是机构的一个重要参数,是判断机构是否具有确定运动的重要依据[1-4]。在应用契贝谢夫-克鲁伯(Grübler-Kutzbach)经典公式
在机构中,当两个构件组成运动副时,将引入限制两构件相对运动的约束。如果用运动副连接的是两构件上运动轨迹重合的点,则该连接将带入一个虚约束。在平面机构中常用到的运动副主要包括转动副、移动副、平面高副等。以下分析在这些运动副处存在轨迹重合虚约束情况。
1) 转动副。
如图1所示,构件1和构件2组成转动副P。假设两构件在没有组成转动副前,构件1上P点的速度为
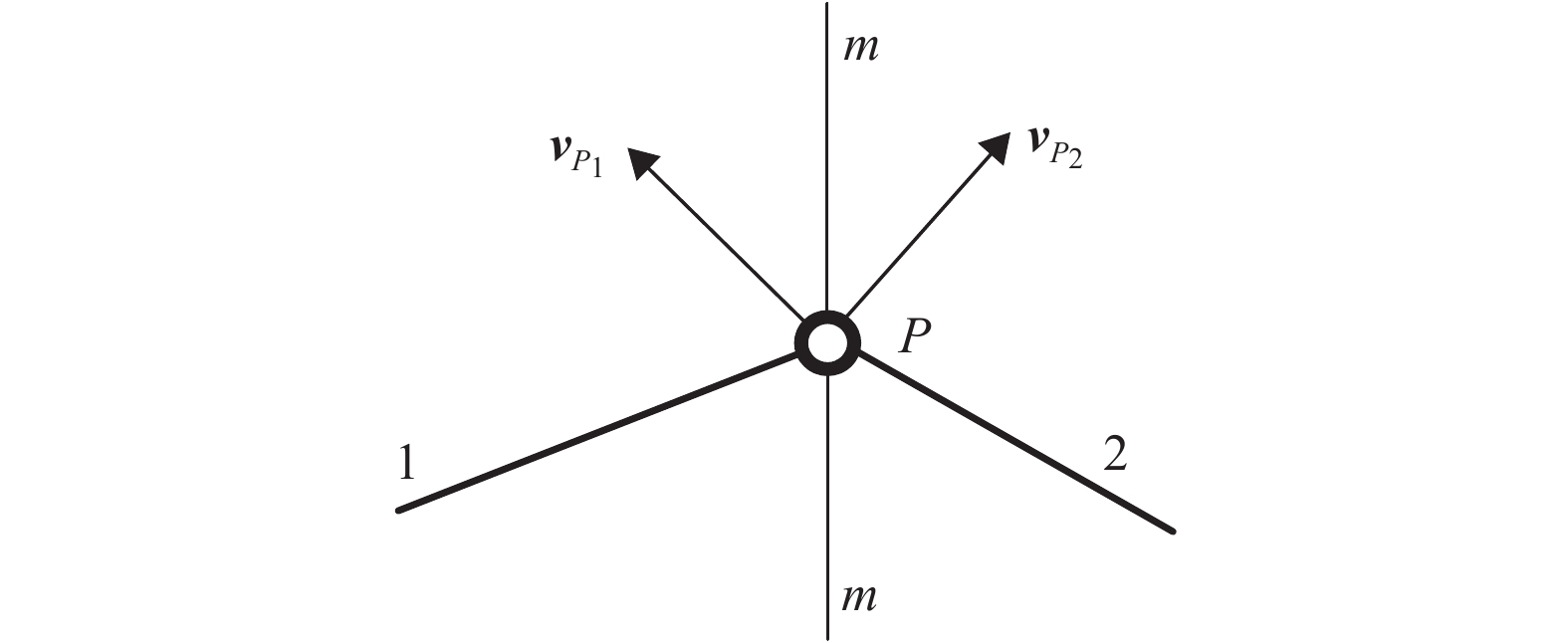
|
图 1 转动副轨迹重合虚约束 Figure 1 Redundant constraints of trajectory coincidence in revolute pair |
2) 移动副。
如图2所示,构件1和构件2组成移动副,m-m方向为垂直移动副导路方向,P为两构件上的一个位置重合点。假设两构件在没有组成移动副前,构件1上P点的速度为
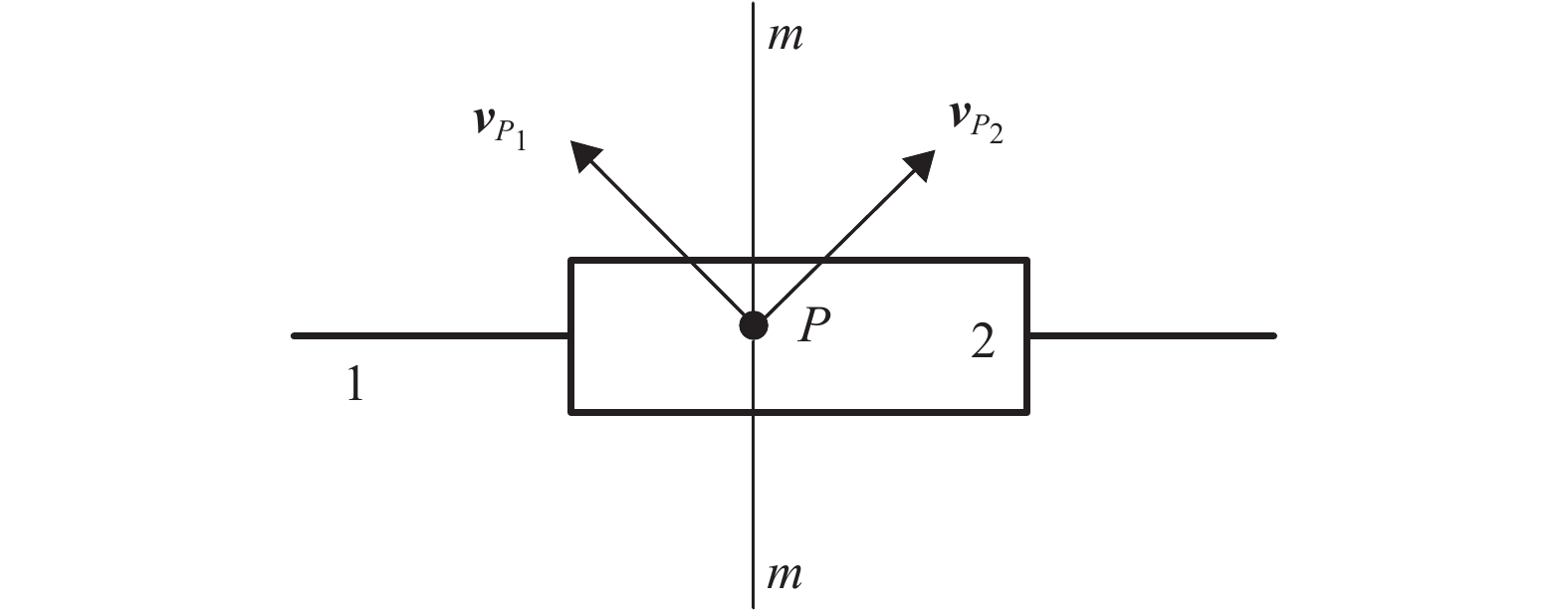
|
图 2 移动副轨迹重合虚约束 Figure 2 Redundant constraints of trajectory coincidence in prismatic pair |
3) 平面高副。
如图3所示,构件1和构件2组成平面高副,接触点为P,n-n方向为过P点的公法线方向。假设两构件在P点没有组成平面高副前,构件1上P点的速度为
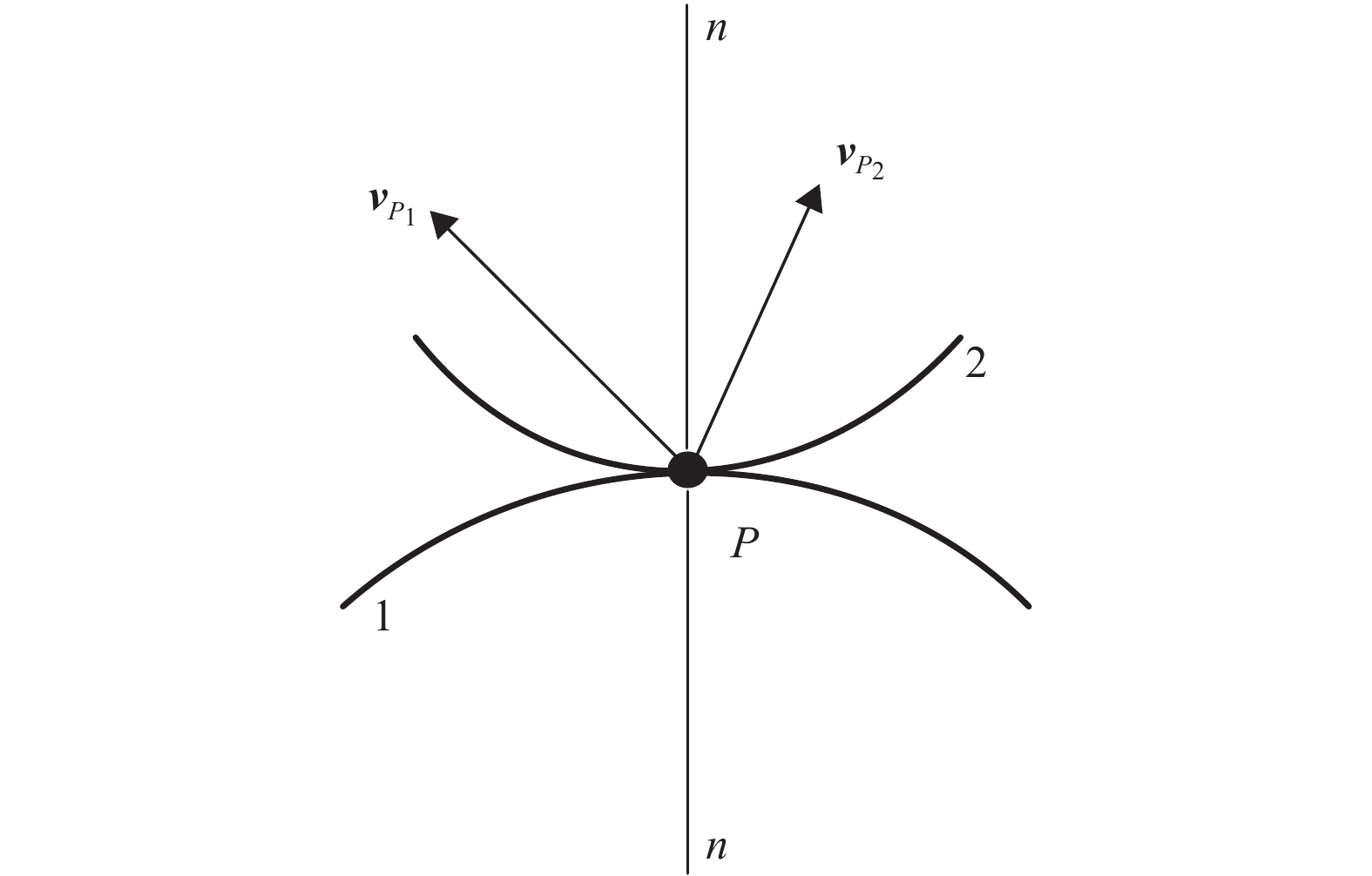
|
图 3 平面高副轨迹重合虚约束 Figure 3 Redundant constraints of trajectory coincidence in planar higher pair |
在机构自由度求解中当存在虚约束时,要将虚约束去除。对于轨迹重合虚约束,其本质是轨迹重合点沿速度垂线方向没有相对运动,当在该方向加入约束即是多余的约束,要去除该约束。
1) 转动副。
对于图1所示的转动副,构件1和构件2在P点组成转动副后,两构件只能围绕P点做相对转动,过P点沿m-m方向和其垂线方向的相对移动将受到限制,即在m-m和其垂线方向各施加一个约束。若两构件在未组成转动副之前,两构件上的P点的速度在m-m方向的分速度
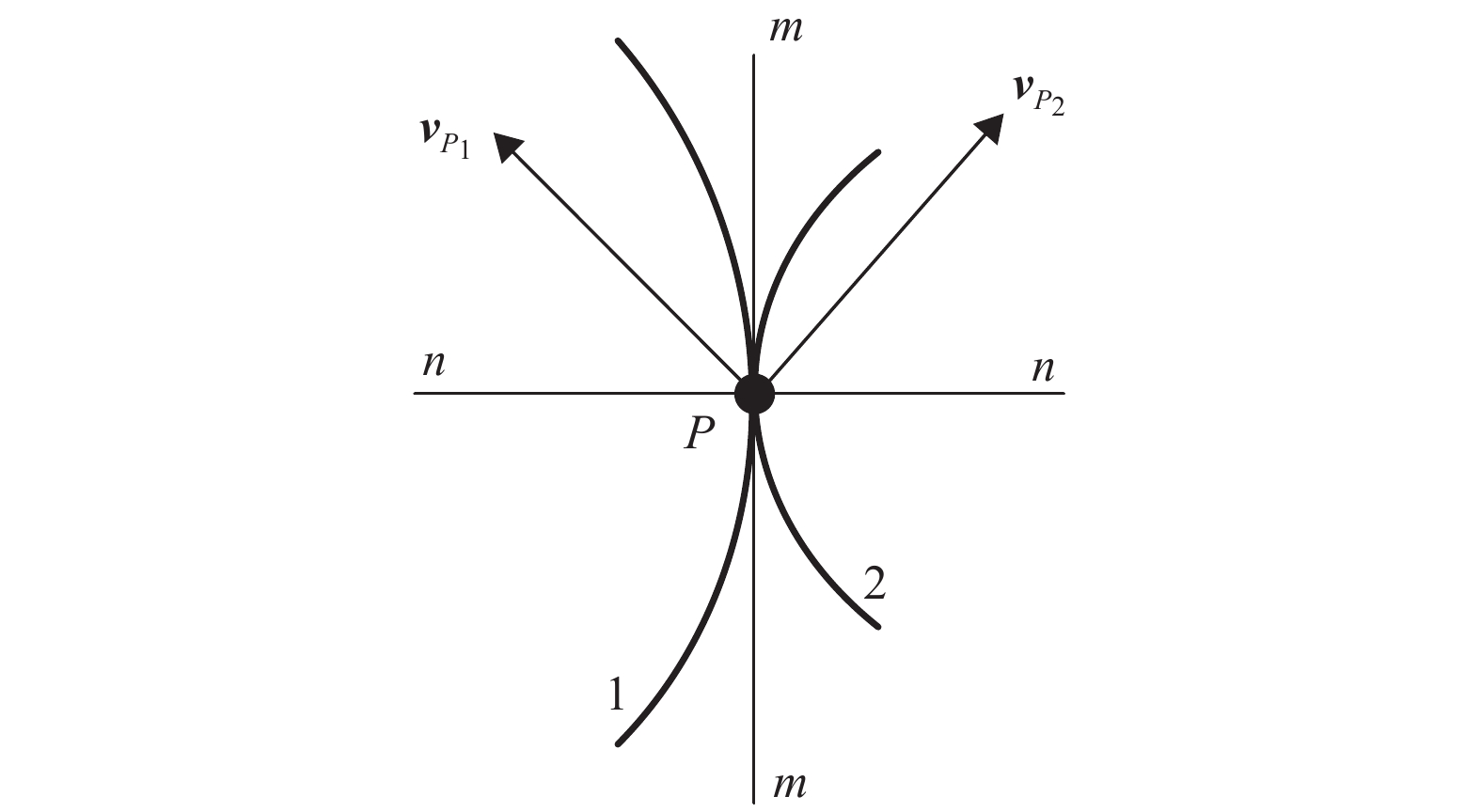
|
图 4 转动副轨迹重合虚约束去除 Figure 4 Removal of redundant constraints of trajectory coincidence in revolute pair |
2) 移动副。
对于图2所示的移动副,构件1和构件2在组成移动副后,两构件只能沿导路方向相对移动,过P点沿m-m方向的相对移动以及围绕P点的相对转动将受到限制,即在m-m移动方向和围绕P点转动方向各施加一个约束。若两构件在未组成移动副之前,两构件上的P点的速度在m-m方向的分速度
对于移动副,若移动副带入的转动约束是虚约束,则去除转动虚约束后移动副将变成公法线为垂直导路方向的平面高副。一个平面低副引入2个约束,若去除2个约束将解除该平面低副。
3) 平面高副。
对于图3所示的平面高副,构件1和构件2在P点组成平面高副后,将在公法线n-n方向施加一个移动运动约束,限制两构件沿该方向的相对移动。若两构件在未组成平面高副之前,两构件上的P点的速度在n-n方向的分速度
下文将以包含轨迹重合虚约束的机构为例,研究虚约束在机构运动副中存在的情况。
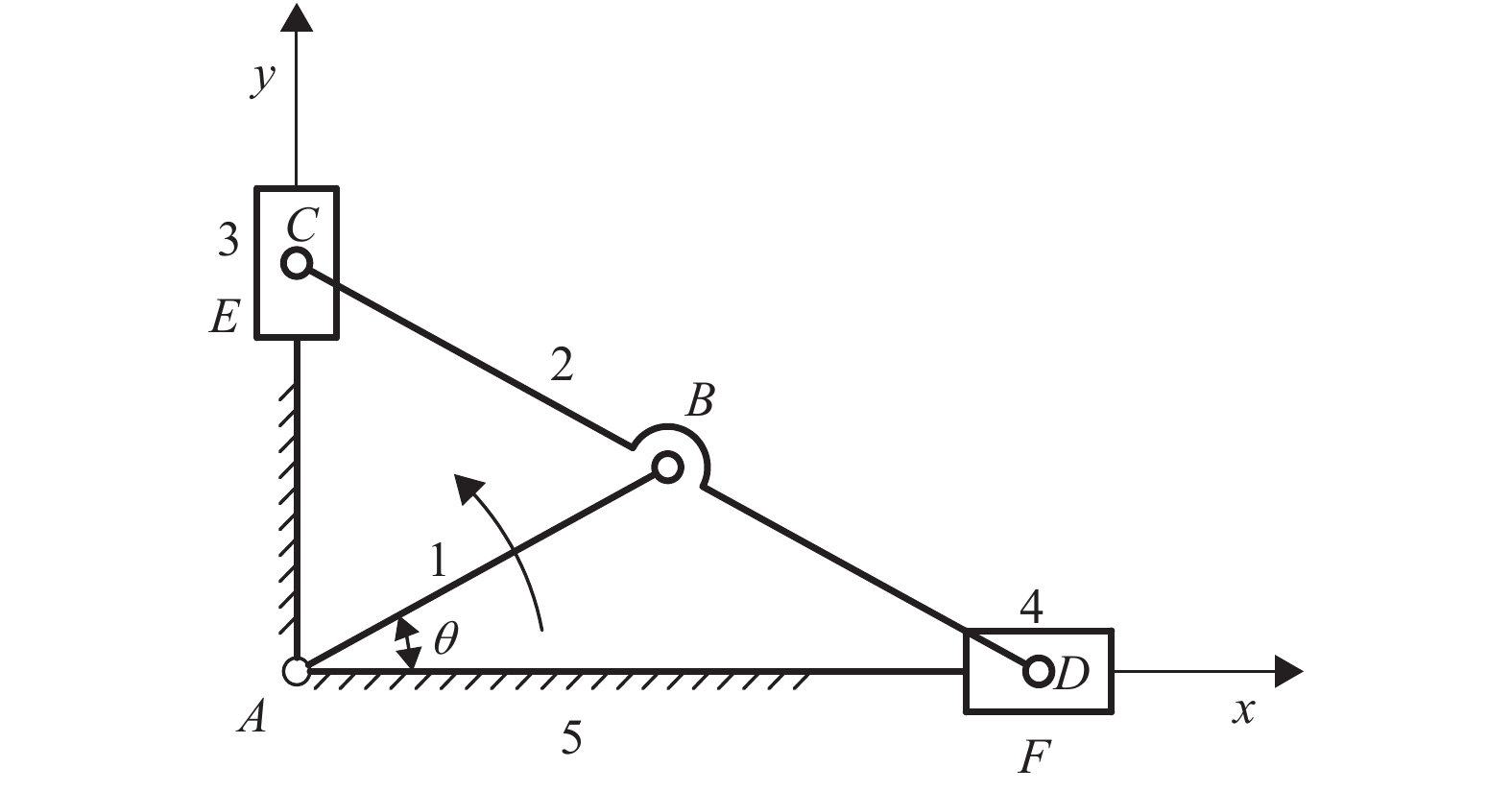
2 举例 2.1 椭圆仪机构如图5所示为一椭圆仪机构,其中LBC =LBD。A、B、C、D为转动副,E、F为互相垂直的移动副。
|
图 5 椭圆仪机构 Figure 5 Elliptic mechanism |
1) 机构自由度计算。
对该机构进行自由度计算可得:F=3×4−2×6=0。而已知该机构的原动件为构件1,且能正常工作,所以该机构自由度应当等于1,说明该机构存在一个虚约束。
2) 约束存在的位置。
(1) 运动副A和B。
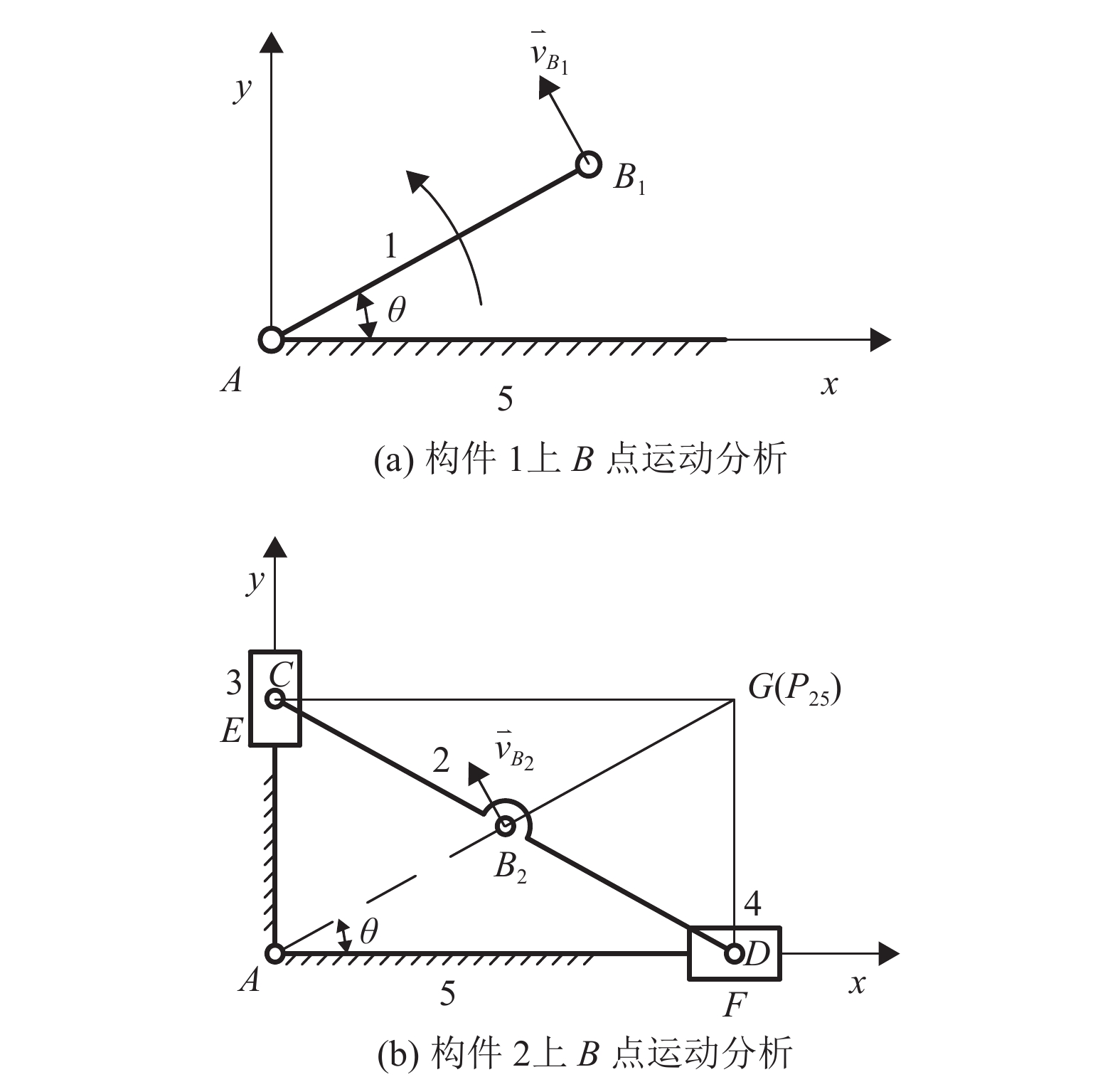
以图5椭圆仪机构上构件1和构件2组成的转动副中心B点为研究对象,假设将转动副B拆除,对构件1上的B1点和构件2上的B2点进行运动分析。
对于B1点,
对于B2点,根据三心定理[15]可得G(P25)点的位置,设lCD=2a,lBG=b,∠BAD=θ,可得:
| ${l_{AB}} = a,{l^2}_{DG} = {a^2} + {b^2} - 2ab\cdot{\rm{cos}}\;2\theta = {\rm{ }}{\left( {a + b} \right)^2}\cdot{\rm{si}}{{\rm{n}}^2}\;\theta $ |
得a=b,则四边形ACGD为矩形,可知A、B、G三点共线,
|
图 6 椭圆仪机构中B点运动分析 Figure 6 Kinematic analysis of point B in elliptic mechanism |
B1和B2运动轨迹均沿垂直AB杆方向,而沿AB杆方向即运动轨迹垂线方向相对位移始终为0,当构件1和构件2在B点组成转动副后,则将在沿AB杆方向引入一个轨迹重合虚约束。
根据结构可知,A、B两点间的距离在机构运动过程中始终保持不变,可以看作是引入一个距离不变虚约束[2]。因此距离不变虚约束可以看作是轨迹重合虚约束的特例,即轨迹重合,重合轨迹恰好是圆。
同样的分析方法也适用于转动副A。可以得出,当构件1和构件5在A点组成转动副后,则将在沿AB杆方向引入一个轨迹重合虚约束。
(2) 运动副C和D。
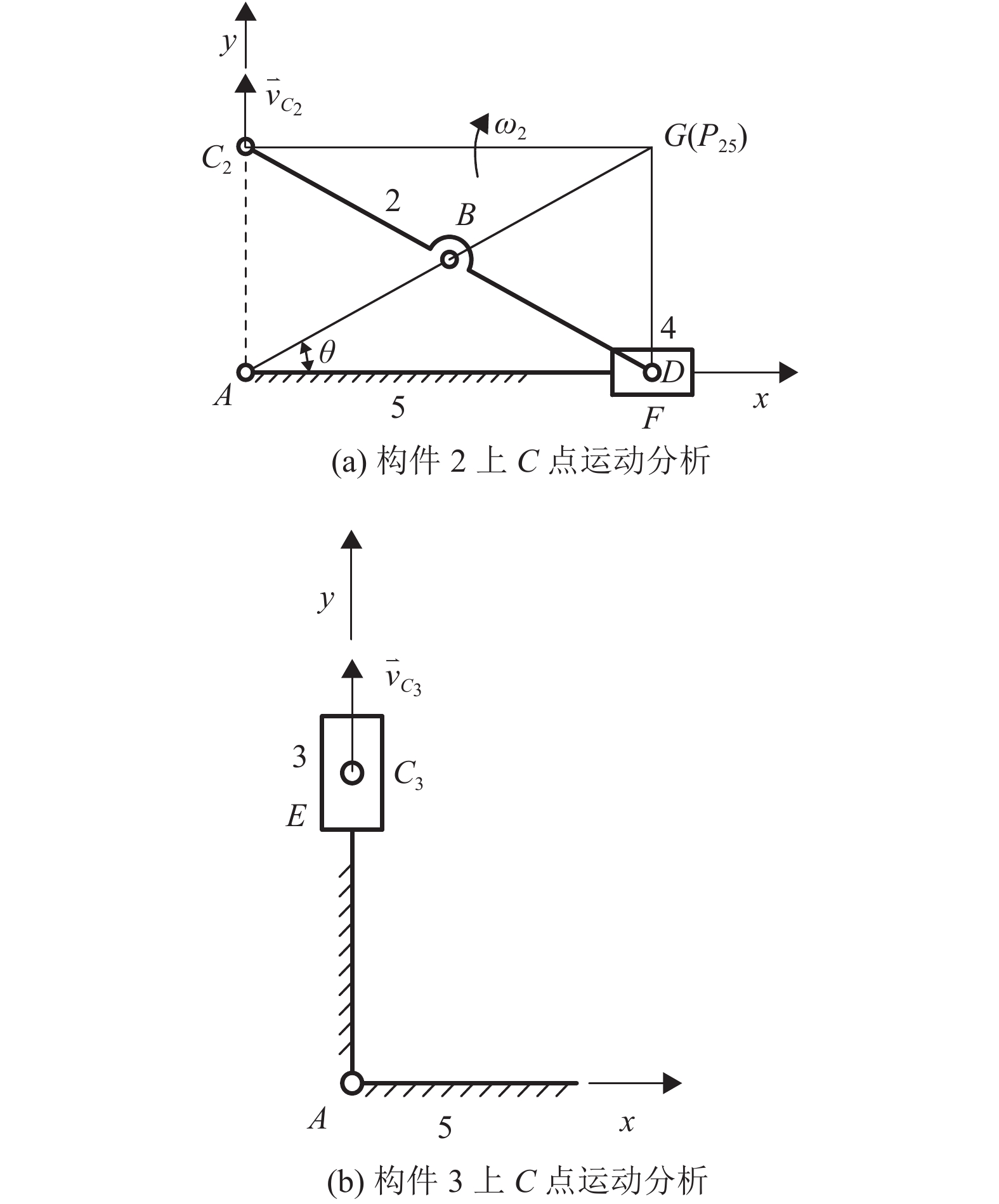
以图5椭圆仪机构上构件2和构件3组成的转动副中心C点为研究对象,假设将转动副C拆除,对构件2上的C2点和构件3上的C3点进行运动分析。
对于C2点,由G(P25)点的位置,可得:
|
图 7 椭圆仪机构中C点运动分析 Figure 7 Kinematic analysis of point C in elliptic mechanism |
对于C3点,构件3与机架5组成移动副,
C2和C3两点的运动轨迹均沿y轴方向。两点沿x轴相对位移始终为0。当构件2和构件3在C点组成转动副后,则将在x方向引入一个轨迹重合虚约束。该结论与文献[2]分析一致。
同样的分析方法也适用于转动副D。可以得出,当构件2和构件4在D点组成转动副后,则将在y方向引入一个轨迹重合虚约束。
(3) 运动副E和F。
以图5椭圆仪机构上构件3和构件5组成的移动副E点为研究对象,假设将移动副E拆除,对构件3进行运动分析。
证明发现[16],滑块3只有相对机架5绕C点的转动,不可能产生垂直于导路方向(即x方向)的相对移动。
当构件3和构件5组成转动副E后,将在垂直于导路方向(即x方向)引入一个轨迹重合虚约束。同样的分析方法也适用于移动副F,可以得出当构件4和构件5组成移动副F后,则将在垂直于导路方向(即y方向)引入一个轨迹重合虚约束。
从以上分析我们可以看出,对于椭圆仪机构中存在的一个轨迹重合虚约束,可以看作是存在于A、B、C、D、E或F中的任一个运动副上,并不存在于某个固定的运动副中。
3) 虚约束的低副高代。
为了便于理解机构结构和计算机构自由度,对上述椭圆仪机构中存在的轨迹重合虚约束进行去除处理。机构中包含一个轨迹重合的虚约束时,理论上可以对任何一个运动副进行处理去除虚约束,但原动件和执行构件常采用平面低副与机架相连,一般不做处理。图5的椭圆仪机构,因运动副A连接原动件与机架,E、F运动副连接执行构件与机架,且若去除移动副E或F垂直导路方向的移动约束,没有合适的运动副表达该连接方式,所以不在运动副A、E和F处进行虚约束去除,可以选择在运动副B、C以及D去除虚约束。分别在运动副B,C点去除虚约束后的机构如下图8(a)和图8(b)所示。对图8(a)机构进行自由度计算可得:F=3×4−2×5−1=1,原动机数目为1,机构具有确定运动。对图8(b)机构进行自由度计算可得:F=3×4−2×5−1=1,原动机数目为1,机构具有确定运动。

|
图 8 去除轨迹重合虚约束后的椭圆仪机构 Figure 8 The elliptic mechanism after removing the redundant constraint of trajectory coincidence |
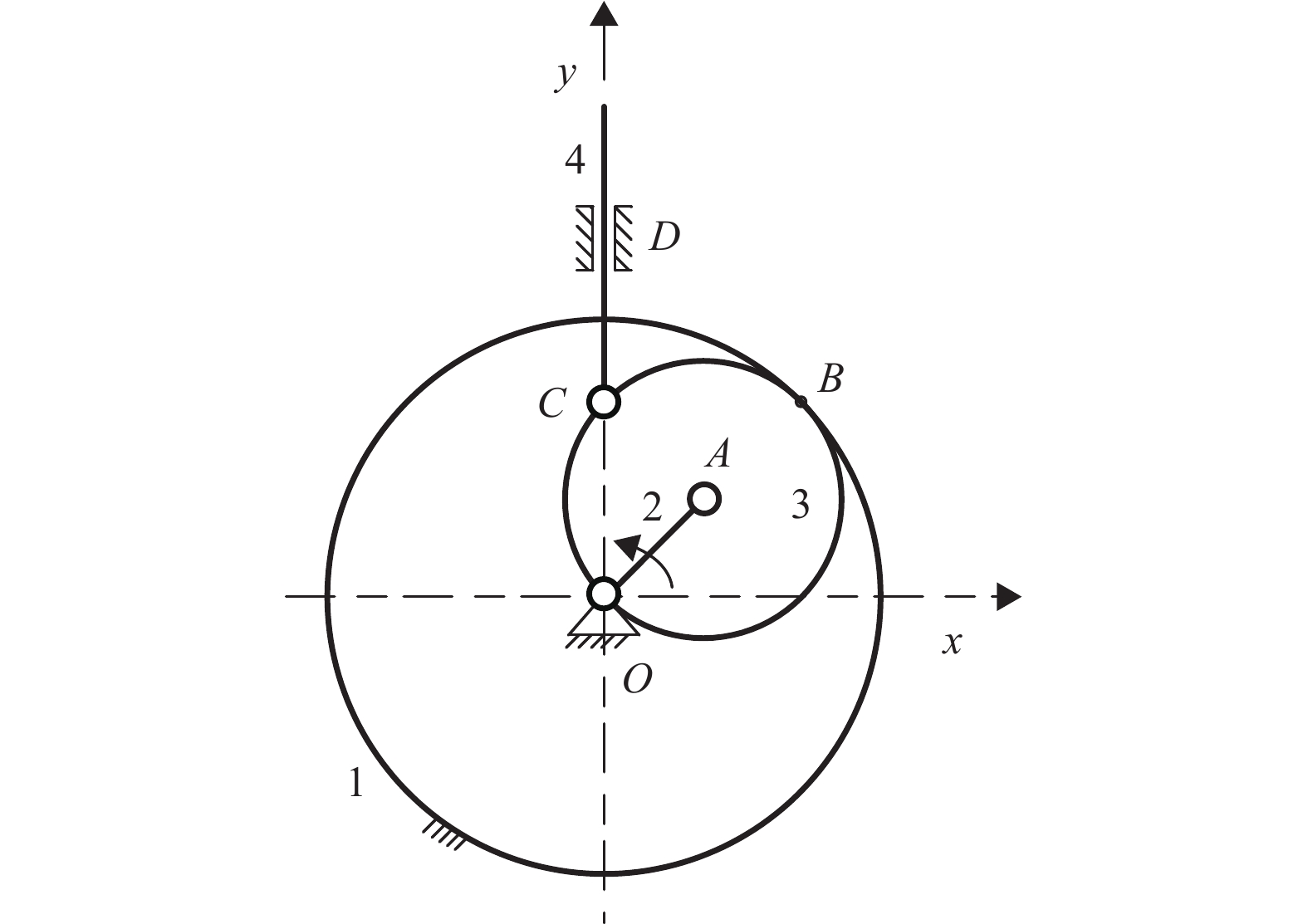
图9所示为齿轮直线机构。A为齿轮3的几何中心,C为齿轮3上点,且R1=2R3=2LOA。
1) 机构自由度计算。
对该机构进行自由度计算可得:F=3×3−2×4−1=0。而已知该机构原动件为构件2,且能正常工作,所以该机构自由度应当等于1,说明该机构同样存在一个虚约束。
2) 虚约束存在的位置。
(1) 运动副A和O。
以图9齿轮直线机构上构件2和构件3组成的转动副中心A点为研究对象,假设将转动副A拆除,对构件2上的A2点和构件3上的A3点进行运动分析。
对于A2点,
对于A3点,B为齿轮3与机架1的瞬心P13,根据三心定理可得O、A、B三点共线,
|
图 9 齿轮直线机构 Figure 9 Gear-linear mechanism |
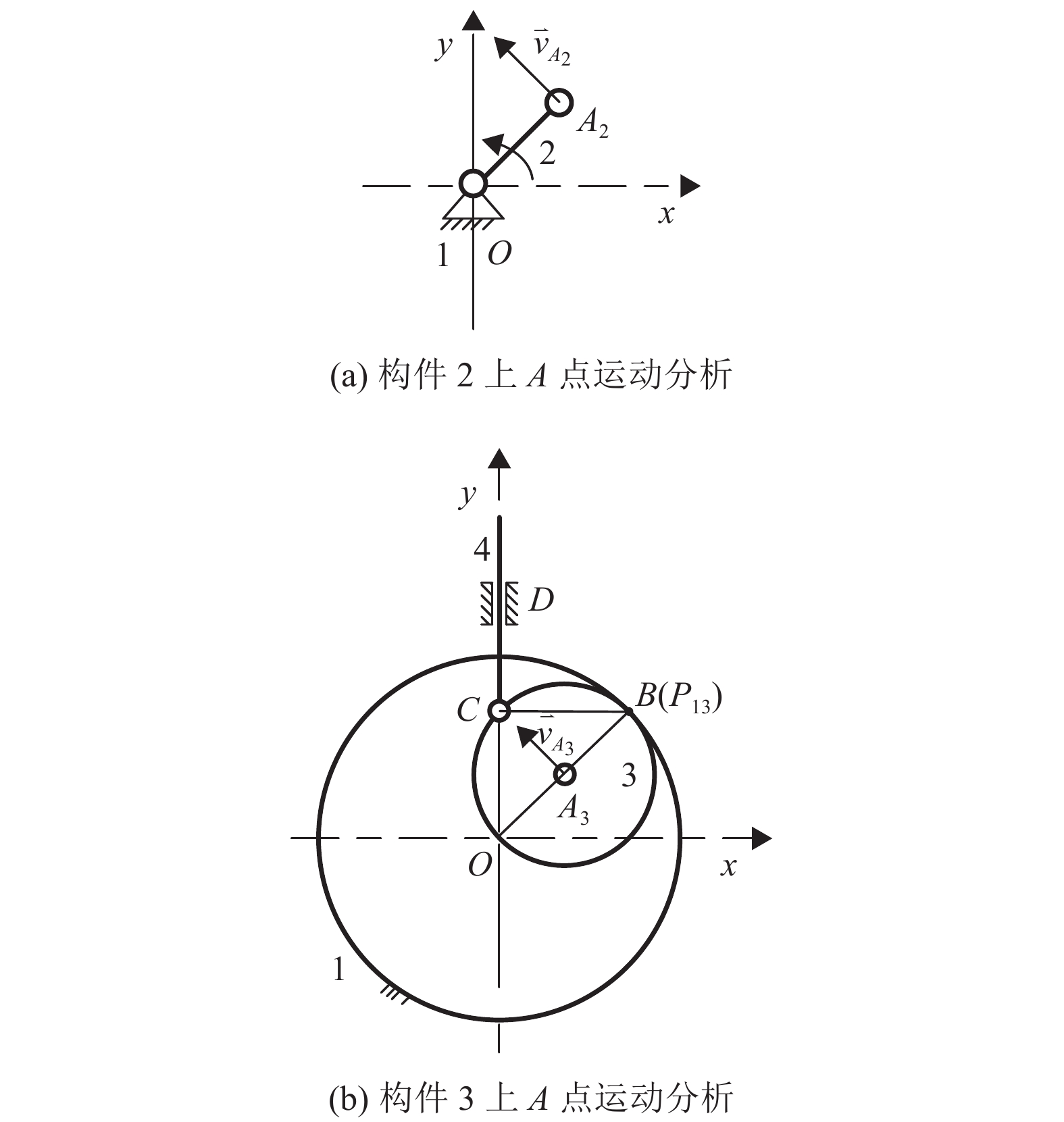
|
图 10 齿轮直线机构中A点运动分析 Figure 10 Kinematic analysis of point A in gear-linear mechanism |
A2和A3运动轨迹均沿垂直OA杆方向,而沿AB杆方向即运动轨迹垂线方向相对位移始终为0,当构件2和构件3在A点组成转动副后,则将在沿OA杆方向引入一个轨迹重合虚约束。
O和A两点在机构运动过程中距离始终保持不变,亦可看作是引入一个距离不变虚约束。再一次说明距离不变虚约束是轨迹重合虚约束的特例。
同样的分析方法也适用于转动副O。可以得出,当构件1和构件2在O点组成转动副后,则将在沿OA杆方向引入一个轨迹重合虚约束。
(2) 运动副B。
以图9齿轮直线机构上构件1和构件3组成的转动副中心B点为研究对象,假设将转动副B拆除,对构件1上的B1点和构件3上的B3点进行运动分析。
对于B1点,其速度
对于B3点,根据三心定理可知P13在OA连线上,亦在过C点OC垂线上,即交点B处,即
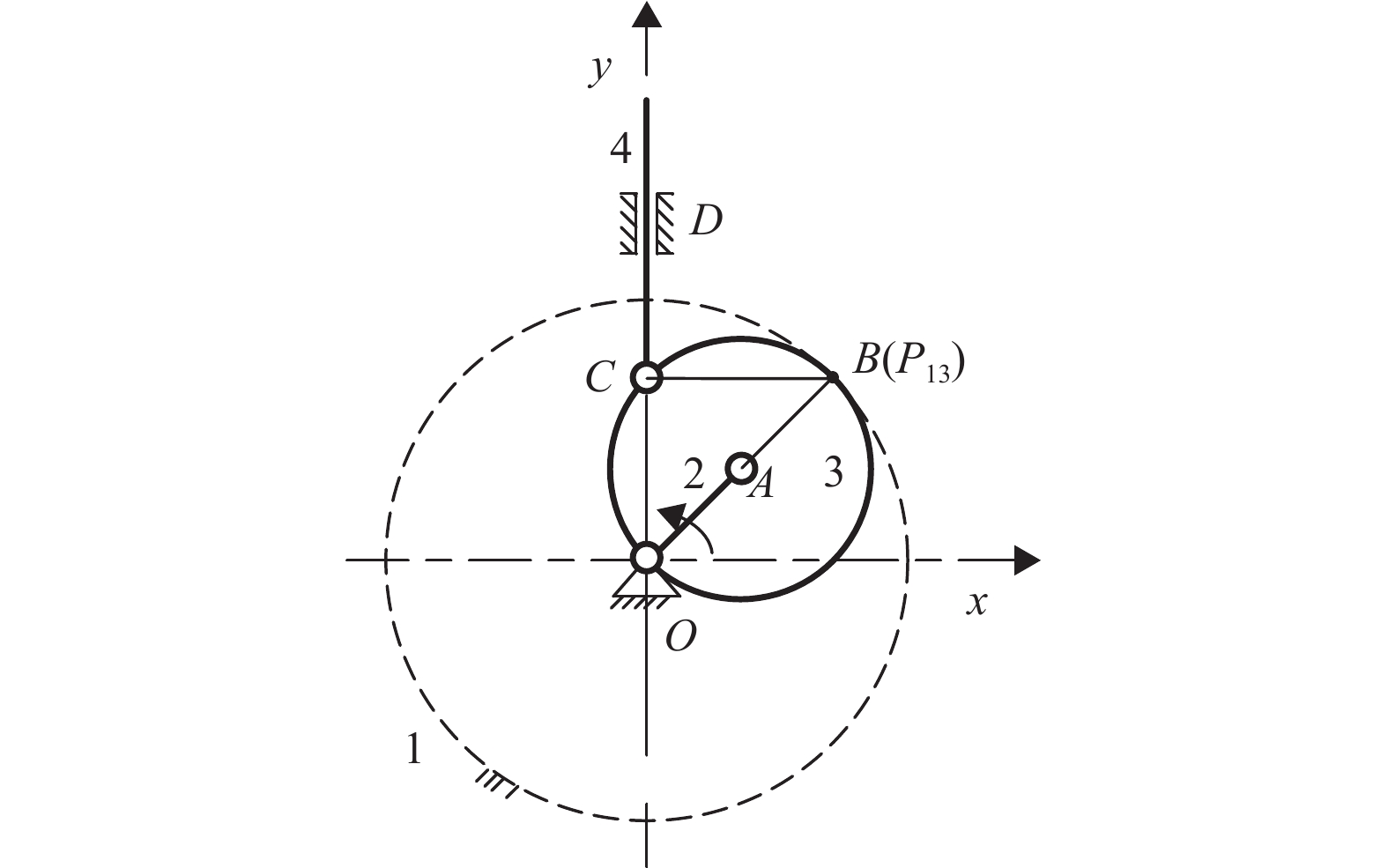
|
图 11 齿轮直线机构中B点运动分析 Figure 11 Kinematic analysis of point B in gear-linear mechanism |
B1和B3运动轨迹相同,当构件1和构件3在B点组成平面高副,将限制两构件在B点沿公法线OB方向的相对运动,即增加1个约束。而在未组成平面高副B前,
(3) 运动副C。
以图9齿轮直线机构上构件3和构件4组成的转动副中心C点为研究对象,假设将转动副C拆除,对构件3上的C3点和构件4上的C4点进行运动分析。
对于C3点,根据三心定理可得O、A、B三点共线,其中B为构件1和构件3的瞬心P13。C点为齿轮3节圆上的点,若连接OC、BC,可知OC⊥BC,可得
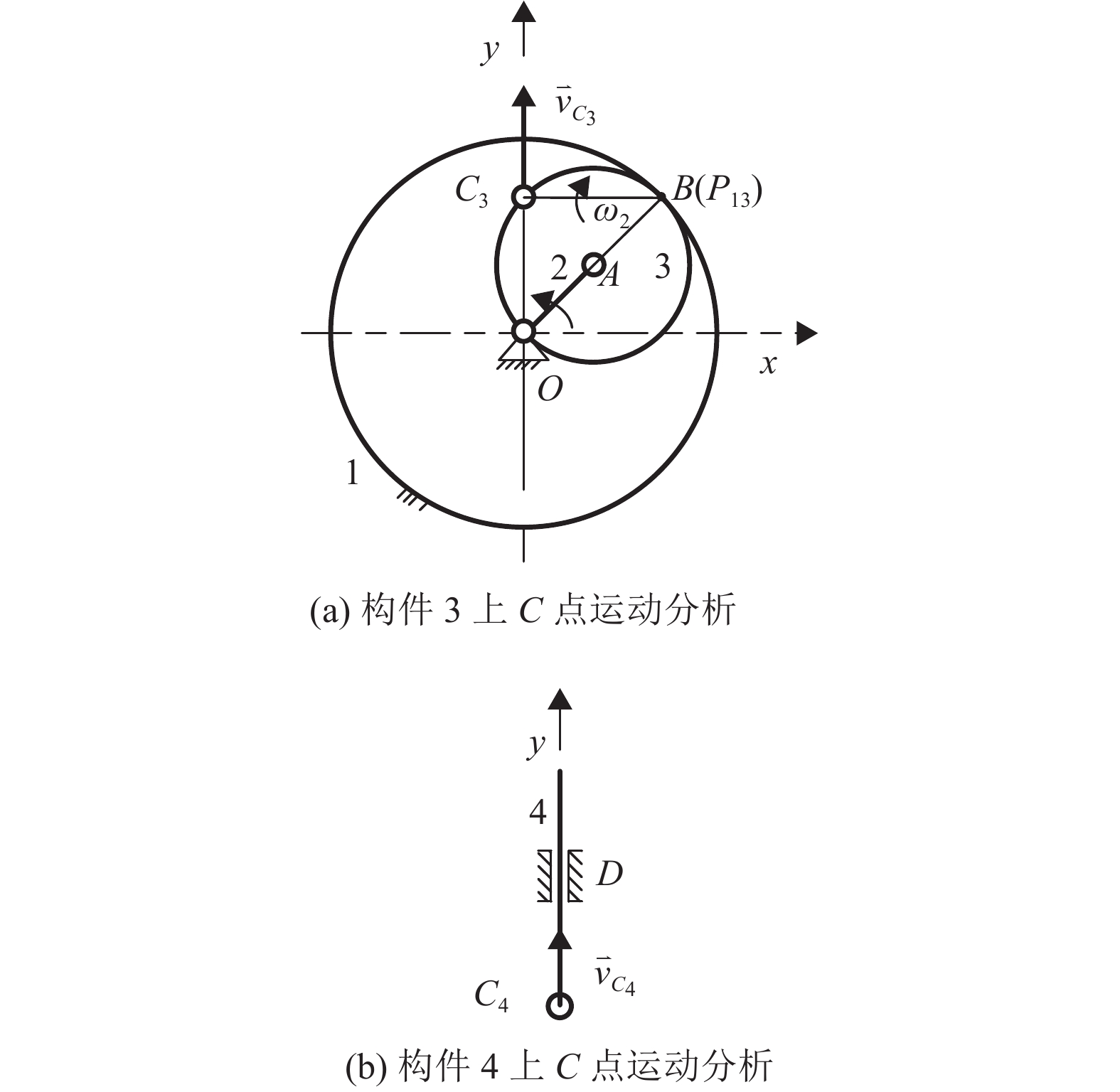
|
图 12 齿轮直线机构中C点运动分析 Figure 12 Kinematic analysis of point C in gear-linear mechanism |
对于C4点,构件4与机架1组成移动副,
C3和C4运动轨迹均沿y轴方向。沿x轴相对位移始终为0。当构件3和构件4在C点组成转动副后,则将在x方向引入一个轨迹重合虚约束。
(4) 运动副D。
以图9齿轮直线机构上构件4和构件1组成的移动副D点为研究对象,假设将移动副D拆除,对构件4进行运动分析。
滑块4只有相对机架1绕C点的转动,不可能产生垂直于导路方向(即x方向)的相对移动。当构件4和构件1组成转动副D后,将在垂直于导路方向(即x方向)引入一个轨迹重合虚约束。
从以上分析同样也可以看出,对于齿轮直线机构中存在的一个轨迹重合虚约束,可以看作是存在于O、A、B、C或D中的任一个运动副上,并不存在于某个固定的运动副中。
3) 虚约束的低副高代。
对上述齿轮直线机构中存在的虚约束进行去除处理。考虑原动件与机架组成低副O,以及移动副D在去除垂直导路方向的移动约束后,没有合适的运动副表达连接方式,对上图9的齿轮直线机构在运动副A、B、C点去除虚约束处理后的机构分别如下图13(a)、图13(b)和图13(c)所示。对图13(a)机构进行自由度计算可得:F=3×3–2×3–1×2=1,原动机数目为1,机构具有确定运动。对图13(b)机构进行自由度计算可得:F=3×3–2×4=1,原动机数目为1,机构具有确定运动。对图13(c)机构进行自由度计算可得:F=3×3–2×3–1×2=1,原动机数目为1,机构具有确定运动。
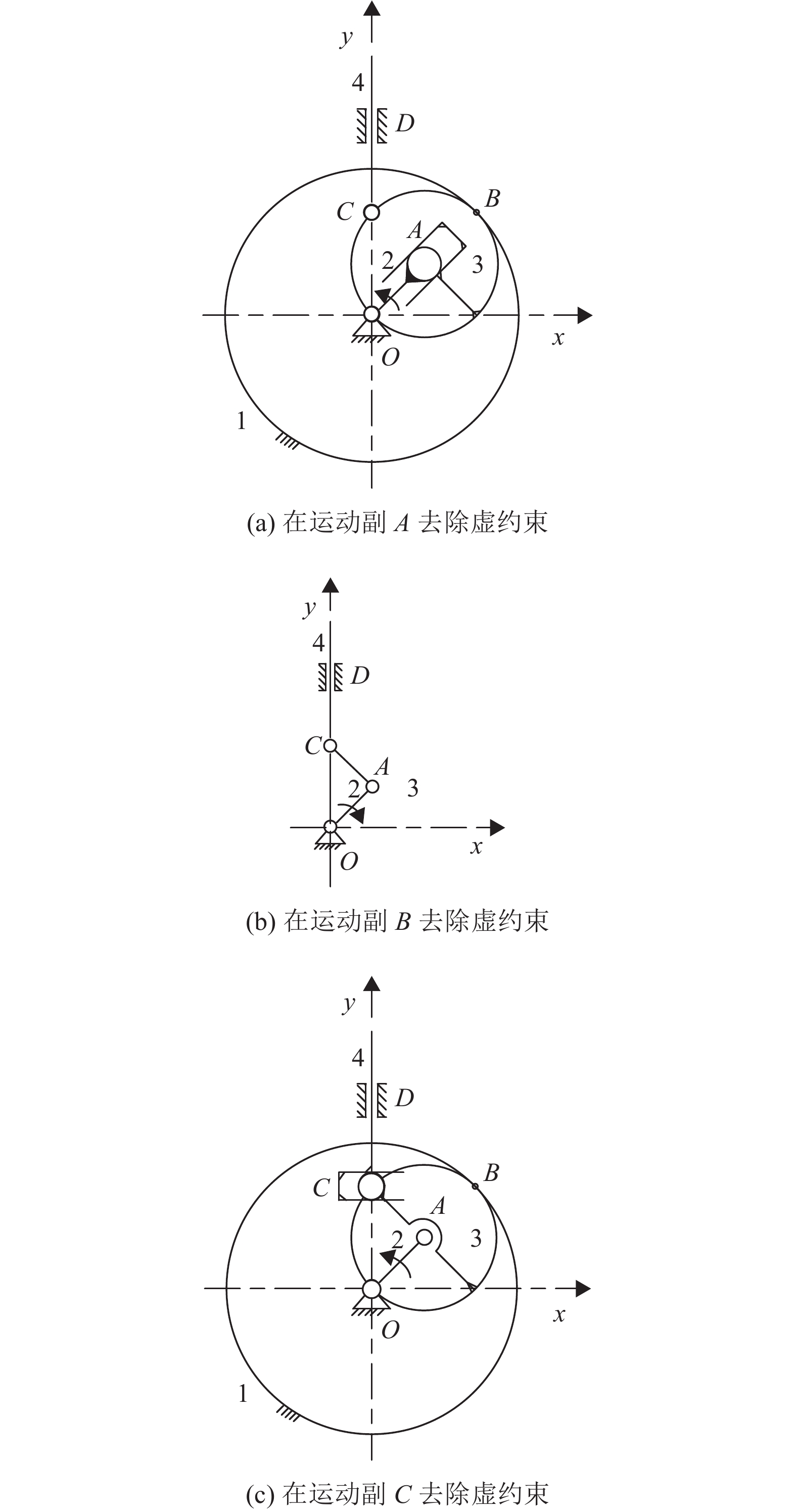
|
图 13 去除轨迹重合虚约束后的齿轮直线机构 Figure 13 The gear-linear mechanism after removing the redundant constraint of trajectory coincidence |
当机构中存在虚约束时,对于转动副,去除一个移动虚约束将变成平面高副。对于移动副,若去除转动虚约束后将变成平面高副,若去除垂直导路方向的移动虚约束,没有合适的运动副表达该连接方式。对于平面低副去除两个虚约束将解除运动副,对于平面高副去除一个虚约束将解除运动副。若在不减少构件数目的基础上,当机构中存在轨迹重合虚约束时,可以采用在转动副处去除一个移动虚约束,将转动低副变成平面高副,即低副高代的方式去除轨迹重合虚约束。
3 结论文中针对平面机构中轨迹重合虚约束进行分析,得出若平面机构中存在轨迹重合虚约束,该虚约束并不存在于某个固定的运动副上,两构件距离不变两点间加入构件和运动副类虚约束是轨迹点重合虚约束的特例,在不减少构件数目的情况下可以采用将转动低副变成平面高副,即低副高代法去除虚约束。该研究有助于对轨迹重合虚约束概念的加深理解以及机构创新设计。
| [1] |
孙桓, 陈作模, 葛文杰. 机械原理[M]. 8版. 北京: 高等教育出版社, 2013.
|
| [2] |
杨可帧, 程光蕴. 机械设计基础[M]. 6版. 北京: 高等教育出版社, 2014.
|
| [3] |
张国英, 姜浩, 张涛, 等. 三自由度类球面并联机构的动力学建模及分析[J].
广东工业大学学报, 2018, 35(6): 24-30.
ZHANG G Y, JIANG H, ZHANG T, et al. Dynamic modeling and analysis of 3-DOF spheroid parallel mechanism[J]. Journal of Guangdong University of Technology, 2018, 35(6): 24-30. DOI: 10.12052/gdutxb.180081. |
| [4] |
郭卫东. 机械原理[M]. 2版. 北京: 科学出版社, 2013.
|
| [5] |
张策. 机械原理与机械设计[M]. 北京: 机械工业出版社, 2004.
|
| [6] |
申永胜. 机械原理教程[M]. 2版. 北京: 清华大学出版社, 2006.
|
| [7] |
韩建友, 杨通, 于靖军. 高等机构学[M]. 2版. 北京: 机械工业出版社, 2015, 9-18.
|
| [8] |
郭卫东, 于靖军. 一种计算平面机构自由度的新方法[J].
机械工程学报, 2013, 49(7): 125-129.
GUO W D, YU J J. A new method of mobility calculation for planar mechanisms[J]. Journal of Mechanical Engineering, 2013, 49(7): 125-129. |
| [9] |
佟士懋. 探讨利用速度瞬心法鉴别平面机构的虚约束[J].
北京联合大学学报, 2011, 25(1): 41-45.
TONG S M. Identification of redundant constraint(s) in a planar mechanism using either the graph of instantaneous centers or the property of the graph’s adjacency matrix[J]. Journal of Beijing Union University, 2011, 25(1): 41-45. DOI: 10.3969/j.issn.1005-0310.2011.01.009. |
| [10] |
冯永伟, 钱瑞明. 机构自由度计算中虚约束问题探析[J].
机械设计与制造工程, 1999, 20(3): 241-244.
FENG Y W, QIAN R M. Study on counting of virtual constraint degrees in mechanism[J]. Machinery Design & Manufacture, 1999, 20(3): 241-244. |
| [11] |
张敏. 虚约束消除方法的研究[J].
新疆石油学院学报, 2003, 15(2): 63-67.
ZHANG M. Study on removal of false restraint[J]. Journal of Xinjiang Petroleum Institute, 2003, 15(2): 63-67. DOI: 10.3969/j.issn.1673-2677.2003.02.016. |
| [12] |
吴文兵, 张云秀. 平面机构自由度的计算[J].
装备制造技, 2016(4): 266-268.
WU W B, ZHANG Y X. The calculation of degrees of freedom of planar mechanism[J]. Equipment Manufacturing Technology, 2016(4): 266-268. |
| [13] |
赵燕, 王琨, 李硕. 平面机构自由度计算中几个问题的探讨[J].
机械管理开发, 2009, 24(6): 36-37.
ZHAO Y, WANG K, LI S. Discussion on the calculation of plane-mechanism movement’s number[J]. Mechanical Management and Development, 2009, 24(6): 36-37. DOI: 10.3969/j.issn.1003-773X.2009.06.017. |
| [14] |
于晓红, 邱丽芳, 韩建友, 等. 特殊情况下机构自由度的计算方法[J].
机械, 2001, 28(6): 20-21.
YU X H, QIU L F, HAN J Y, et al. The calculation of degrees of freedom of mechanism in special conditions[J]. Machinery, 2001, 28(6): 20-21. |
| [15] |
陈再良, 彭玉成, 刘彦昌. 关于三心定理应用中若干问题的探讨[J].
青岛化工学院学报, 1999, 20(3): 241-244.
CHEN Z L, PENG Y C, LIU Y C. On some problems in application of three-link theorem[J]. Journal of Qingdao Institute of Chemical Technology, 1999, 20(3): 241-244. |
| [16] |
黄真, 刘婧芳, 李艳文. 论机构自由度[M]. 北京: 科学出版社, 2011.
|
 2020, Vol. 37
2020, Vol. 37

