2) 中国河北063000唐山地震监测中心站;
3) 中国石家庄050021河北省地震局
2) Tangshan Central Seismic Station, Hebei Province 063000, China;
3) Hebei Earthquake Agency, Shijiazhuang 050021, China
研究表明,多数台站地电阻率变化具有1年尺度的年周期特征,该现象与自然界季节性气象因素以及人类生产、生活影响有关。潜水位变化是年变主要原因之一,它反映了表层含水量的变化,该变化直接影响表层真电阻率变化,从而引起地电阻率变化;另外,潜水位变化受季节灌溉和降雨影响(钱家栋等,1998)。在地震预报领域,与孕震无关的年度变化称为“正常变化”,而与地震有关的震前趋势转折(如下降趋势)或年变畸变等现象,称为“异常变化”,尤其在诸多7级及以上地震事件中,类似异常变化特征尤为典型(王志贤,1981;钱家栋等,1985)。尽管年周期变化看似微不足道,但对中长期数据跟踪分析却具有重要的参考意义。例如,破年变异常、年变幅异常、多年周期尺度分析等,均建立在对多年周期变化特征深入认识的基础上,方能界定为“异常”。因此,精准识别正常年变周期特征,是判断地电阻率数据是否正常的重要因素。
本文通过计算2017—2022年全国地电阻率原始月均值,整理得到26个具有显著年变特征且数据相对稳定的台站,包括东北地区的白城、四平、绥化台,西北地区的嘉峪关、天水中心站、平凉、乾陵台,华北地区的昌黎、阳原、大柏舍、兴济、平谷马坊、宝昌、乌加河、塘沽、青光、徐庄子宝坻新台,华东地区的郯城、高邮、新沂、南京、蒙城台,西南地区的甘孜、腾冲台,华南的河源台。因篇幅有限,各台仅选取数据质量最佳的测道进行分析,旨在探讨地电阻率年变中气象因素(包括气温、气压、降雨量)的影响比例,且同步分析具有地下水测项台站的水位影响,并探寻可能与应力场变化相关的地电阻率趋势异常。在数据预处理阶段,首先消除年变周期影响,并对降雨影响进行评估,若存在则进行去倾处理。
1 数据处理方法(1)多元线性回归。设x1、x2、x3、x4多个参量与变量y有相关关系,建立以下多元线性回归方程:
| $ y=b_0+a_1 x_1+a_2 x_2+a_3 x_3+a_4 x_4 $ | (1) |
式中,y为地电阻率值,x1、x2、x3、x4分别代表气温、气压、地下水位、降雨量,a1、a2、a3、a4代表相应回归系数,b0为常数项。用最小二乘法求出常数项和回归系数,即可建立多元线性回归方程(田山等,2000)。
(2)去年变与去倾处理。地电阻率呈显著年变周期和趋势变化特征,通常与气象因素密切相关,在无显著震情异常情况下,应剔除“无效”年变和趋势变化成分。具体如下:采用傅里叶变换剔除年变,获取残差序列,分析该序列与降雨量之间是否存在多年尺度的趋势相关性,若存在则进行去倾处理。此外,尽管地下水位与地电阻率存在一定相关性,但水位变化与降水量密切相关,故不做二次消除处理。
傅里叶变换去年变周期效果显著(杜学彬等,2017)。以T来表示年变周期长度,即1年中等间隔均值序列包含T个观测值。以
| $ a_n=\frac{2}{T} \sum\limits_{j=n-T+1}^n y_j \cos \frac{2 \pi(j-n+T)}{T} $ | (2) |
| $ b_n=\frac{2}{T} \sum\limits_{j=n-T+1}^n y_i \sin \frac{2 \pi(j-n+T)}{T} $ | (3) |
| $ x_n=a_n \cos \frac{2 \pi(j-n+T)}{T}+b_n \sin \frac{2 \pi(j-n+T)}{T} $ | (4) |
排除年变化的新序列为
| $ G_n=y_n-x_n \quad(n=T, T+1, \cdots, N) $ | (5) |
由式(2)、(3)计算an、bn,二者随年变强弱而动态变化。对yn序列中前T-1个数据通过基波拟合,求得x1、x2、…、xT-1,利用式(5),计算得到G0、G1、…、GT-1。
在去倾处理过程中,设地电观测物理量时序序列为y = {y1, y2, …, yN},线性回归方程为:
| $ y_i^{\prime}=a+b x_i \quad(i=1, 2, \cdots, N) $ | (6) |
剩余回归平方和
| $ R_i=y_i-y_i^{\prime} \quad(i=1, 2, \cdots, N) $ | (7) |
| $ L_i=R_i+a \quad(i=1, 2, \cdots, N) $ | (8) |
式中,
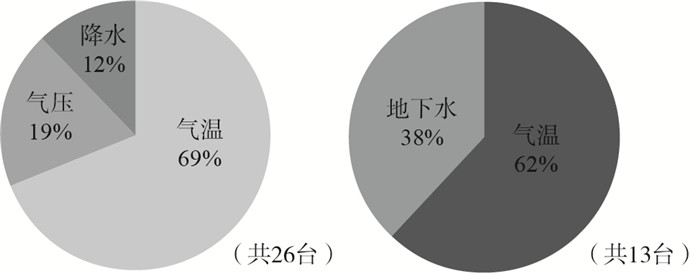
据田山等(2000)对塘沽台的研究,在地电阻率观测中,气压影响占比最大,气温与地下水位影响占比相当,还包括一定比例的湿度。采用多元线性回归方法,计算26个台站2017—2022年气压、气温、降雨量在地电阻率年变中的影响系数(图 1),其中13个台站具有同台同期地下水数据(静水位)。结果显示:在未统计地下水影响的情况下,在26个台站中,气温影响系数最高的台站占比约69%,气压影响系数最高的台站占比约19%,降水影响系数最高的台站占比约12%;在13个统计地下水影响的台站中,气温影响系数最高的台站占比约62%,地下水影响系数最高的台站占比约38%,其他因素影响较小,忽略不计(图 1)。以上分析结果说明,气温对地电阻率观测年变周期影响最大,地下水次之,气压与降雨量影响不明显,二者对年变具有辅助或滞后影响。
|
图 1 影响因素最大影响系数台站占比 Fig.1 Proportion of meteorological factors and maximum impact coefficient stations on groundwater |
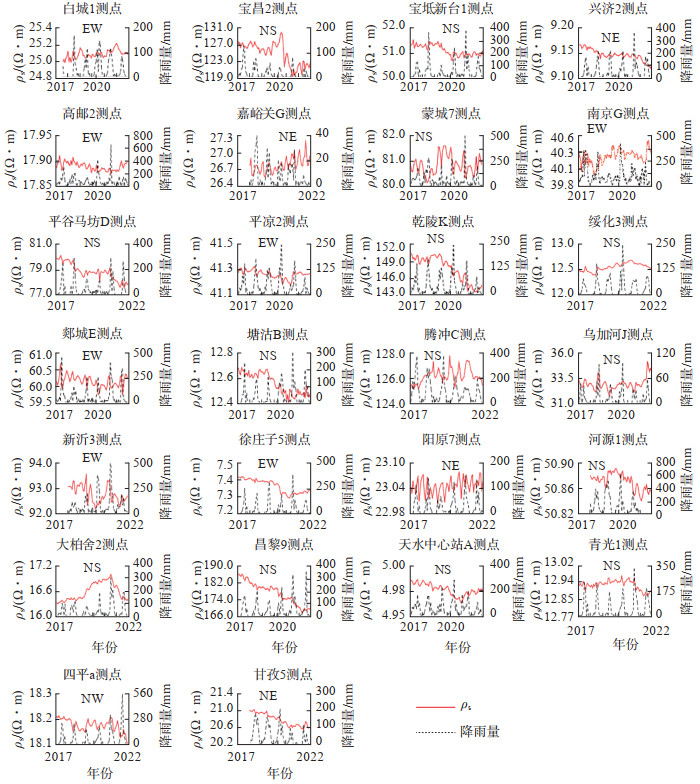
经傅里叶变换去年变周期处理,大柏舍、昌黎、青光、甘孜、四平、天水中心站6个台站的地电阻率残差序列与降雨量趋势相关性明显,其他20个台站相关性不显著(图 2)。由图 2可见:大柏舍台地电阻率残差序列与降雨量趋势多年呈正相关性,即地电阻率随降雨量增大而增大,直至2021年强降雨达极大值,之后二者呈同步下降变化;昌黎台二者多年趋势呈负相关性,即降水量逐年增加,地电阻率逐年下降;青光台、四平台二者均平稳变化,起伏不大,2022年受强降雨影响,地电阻率同步下降,呈负相关性;甘孜台二者变化趋势整体呈正相关性;天水台二者多年趋势呈负相关性,即降水量呈先上升后下降变化,而地电阻率呈先下降后上升变化。该现象说明,年度降雨量的趋势变化与地电阻率长趋势变化在不同台站的影响效应不同。在研究中,大部分台站的地电阻率残差序列与降雨量趋势相关性不明显,与沈红会等(2020)的观点一致。当然,在更大的研究空间内,个别台站二者的相关性仍较显著。
|
图 2 地电阻率去周期残差值与降雨量对比 Fig.2 Comparison of residual values of ground resistivity with precipitation after periodic removal |
分析认为,该现象存在的原因可能是:①地下水位变化对地电阻率影响显著,而降雨量对地下水位变化有一定影响,且降雨影响相对直观,降雨量不同,对地电阻率的持续影响时间不同:非强降雨时,地下水储量变化不大,地电阻率主要受表层介质饱水量影响,降雨影响持续几小时至两三天;强降雨时,表层介质及以下含水层水量增加显著,地电阻率呈显著下降或上升(因台而异)变化,且持续数月甚至1年以上,形成地电阻率的年变畸变。然而,采用傅里叶变换不能有效消除此类畸变,地电阻率残差序列仍会不同程度地保留趋势变化,故上述6个台站需进行第2次降雨趋势处理。②各台站地质环境,如含水层组成、含水层排水和储水情况、介质岩性及孔隙度等不尽相同,即使相同的气象环境或降雨量,对各台地电阻率趋势的影响程度和恢复期也可能不同,无法使用统一标准进行评价。
3 地电阻率趋势分析 3.1 异常趋势特征经去周期去倾处理,对26个台站地电阻率数据进行线性拟合,可见拟合斜率具有上升、下降、平稳3种趋势特征,统计结果见表 1。由表 1可知:①趋势平稳:天水中心站、昌黎、大柏舍、青光、阳原、甘孜、四平台,斜率值精度达小数点后5位以上,数值近零;②趋势上升:白城、蒙城、嘉峪关、南京、绥化、腾冲、乌加河台,斜率为正,与平稳型相比,数值偏高;③趋势下降:宝昌、乾陵、平谷马坊、新沂、徐庄子、郯城、宝坻新台、兴济、河源、高邮、平凉、塘沽台,斜率为负,与平稳型相比,数值偏高。
| 表 1 去周期去倾后地电阻率线性拟合斜率统计 Table 1 Statistics of linear fitting slopes of ground resistivity after removing periods and tilting |
在上述3种趋势背景下,部分台站存在趋势同步转折或扰动现象。以下就此进行深入分析,并结合震情或应力场进行综合探讨。
(1)地电阻率趋势略上升。以蒙城和南京台为例,两台站地电阻率转折变化特征相似,且相距较近(约328 km),选取台站周边一定范围内地震数据,采用最大似然法(薛靖楠等,2011;吴忠良,2021),进行b值区域应力场分析,并将其与地电阻率变化趋势进行同期对比,结果见图 3。
地电阻率变化与地应力场变化密切相关(钱家栋等,1985)。在测震学中,b值是反映区域应力水平的一个指标,该参数来源于震级M与频度N之间的G—R经验关系式,即
| $ \log N=a-b M $ | (9) |
式中,b为统计时段内不同大小地震之间的比例,在最小完整性震级相同情况下,b值越高平均震级越低,b值偏低则代表应力增强,所触发地震震级偏高(Scholz,1968;Wyss,1973)。
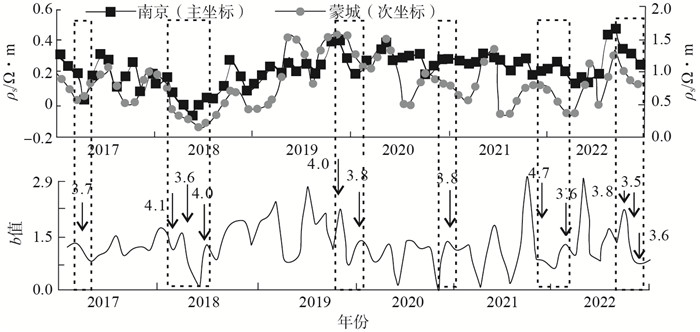
选取(30.7°—34.2°N,115.0°—120.0°E)范围内地震事件(源自统一快报目录,震级标度ML,且予以校正),因该区域地震偏少,最小完整性震级Mc取ML 1.0。计算所选地震的b值,结果见图 3(b),图中仅标注ML≥3.5的地震震级。
|
图 3 蒙城台、南京台地电阻率趋势变化和应力场b值对比 Fig.3 Comparison of trend changes in resistivity and stress field b values between the Mengcheng and Nanjing stations |
由图 3可见:①2017—2022年,两台地电阻率变化整体趋势同步性较好,并与b值变化有一定相关性。如2018年下降、2019年上升、2020—2021年转折下降、2022年转折上升。②研究时段内,共发生ML≥3.5地震12次,多数地震出现在地电阻率和b值相对低值附近,说明地电阻率变化受到区域应力场调整的影响。
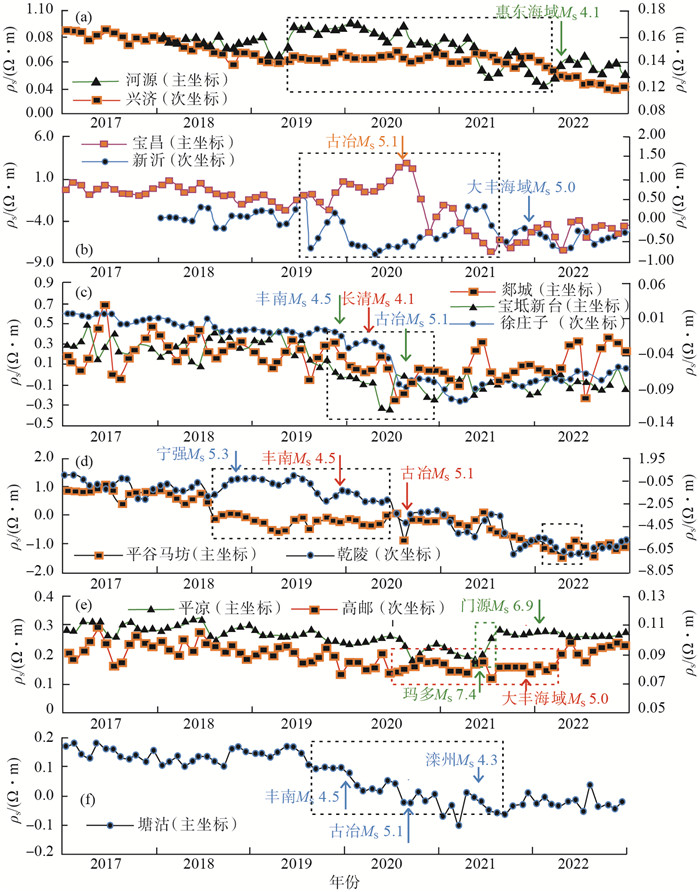
(2)地电阻率趋势略下降。各台站异常主要集中在2019—2022年,但趋势转折时间并不一致,见图 4(虚线框仅表示趋势转折过程的大致时段),图中标注的震例均发生在各台站周边趋势异常期间或异常结束后半年内。震例目录源自中国地震台网中心,选取范围如下:台站周边200 km范围内MS 4.0—4.9地震、300 km范围内MS 5.0—5.9地震、600 km范围内MS 6.0—6.9地震、800 km范围内MS≥7.0地震(3个月内200 km范围内发生的地震视为同一组,挑选震级最大的地震进行分析。
|
图 4 趋势下降型地电阻率多年动态趋势变化 (地震标注文字、箭头与曲线颜色一致表示对应该台异常,文字、箭头颜色不同表示对应2个台站异常,虚线框同理) Fig.4 Multi-year dynamic trend changes of decreasing trend type ground resistivity |
由图 4可见:①兴济、河源台:2019年5月至2022年2月期间,与前后趋势相比,呈明显的阶段性差异,其中兴济台下降速率减缓,而河源台在小幅提升后下降,且2021年年变幅增大。值得注意的是,兴济台异常无震例对应,而河源台在异常结束后2个月内于2022年3月14日发生广东惠东县海域MS 4.1地震(震中距139 km)。②新沂、宝昌台:2019年7月至2021年8月,趋势大幅扰动明显,其中新沂台先下降后小幅提升,宝昌台先上升后快速下降。异常期间于2020年7月12日发生河北古冶MS 5.1地震(震中距宝昌台约355 km),异常结束后约4个月,于2021年11月17日发生江苏大丰海域MS 5.0地震(震中距新沂台约276 km)。③郯城、宝坻新台、徐庄子台:2019年10月至2020年底呈快速下降,达最低值后转折略上升,异常期间于2019年12月5日发生丰南MS 4.5地震(震中距宝坻新台200 km以内),于2020年7月12日发生河北古冶MS 5.1地震(震中距徐庄子台200 km以内),于2020年2月18日发生山东长清MS 4.1地震(震中距郯城台256 km)。④平谷马坊、乾陵台:2018年7月至2020年6月前后,呈阶段性趋势阶升或阶,异常期间发生河北古冶MS 5.1地震、丰南MS 4.5地震(震中距平谷马坊台150 km以内)以及2018年9月12日陕西宁强MS 5.3地震(震中距乾陵台309 km)。2022年3月前后,两台站地电阻率变化趋势由下降转为略上升。⑤高邮、平凉台:2020年6月至2022年3月,高邮台地电阻率变化呈平稳趋势,与前后阶段的略降、略升态势有一定差异,异常期间发生江苏大丰海域MS 5.0地震(震中距高邮台约183 km);2021年5—7月,平凉台地电阻率呈显著的由降转升的变化趋势,后趋于平稳,2021年5月22日青海玛多MS 7.4地震(震中距平凉台759 km)即发生在上升阶段,且数据平稳后约半年,于2022年1月8日发生青海门源MS 6.9地震(震中距平凉台536 km)。⑥塘沽台:2019年8月至2021年8月期间,地电阻率较前后时段下降幅度明显偏大,异常结束后呈平稳变化,异常期间相继发生丰南MS 4.5、河北古冶MS 5.1和滦州MS 4.3地震,且震中距台站均约121 km。
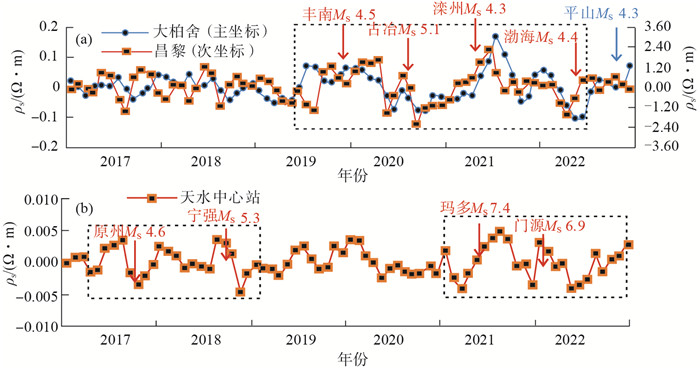
(3)地电阻率趋势平稳。大柏舍、昌黎台和天水中心站地电阻率多年变化形态呈现出较高的相似性,见图 5,可见:2019—2022年,大柏舍与昌黎台数据高度相似,主要特征表现为数据离散度较大,相较于2017—2018年,波动更为显著,其中2020年为低值年、2021年则为极大值年;而天水中心站同期数据离散度偏小,但整体变化趋势与其他两台保持一致性。
|
图 5 大柏舍、昌黎、天水中心站地电阻率多年动态趋势变化 Fig.5 Multi-year dynamic trend of ground resistivity at Dabaishe, Changli, and Tianshui central stations |
2019—2022年,昌黎台地电阻率趋势异常与河北省及附近海域4次中等地震对应较好,而大柏舍台地电阻率变化趋势与该台多年同步,但仅有1次MS 4.3地震与异常对应。在各震例发生前后1年内,地电阻率可能呈上升或下降的异常现象。昌黎与大柏舍台分别位于1976年唐山MS 7.8地震、1966年邢台MS 6.8地震的老震区。通常情况下,唐山老震区中小震活跃度较邢台老震区偏高。虽然如此,两台地电阻率同步异常现象依然表明河北省区域应力场变化具有一致性,作为能量集中释放窗口,发震地点更易出现在断裂带活动相对活跃区域。与天水中心站地电阻率趋势异常相对应的地震共计4个,含4—7级地震各1次,各震例发生前后的趋势异常有上升也有下降,且持续时间均在1年以内。
综上所述,通过对去年变、去倾处理的地电阻率数据进行动态分析,可知部分台站,如蒙城和南京台、大柏舍和昌黎台、徐庄子和宝坻新台,地电阻率呈局域性趋势的同步变化,而多数台站在2019—2022年,则表现为广域性异常的同步变化,且多数震例集中在该时段发生,充分揭示了远源场的调整作用。
4 讨论针对上述多台站同步异常的广域性问题,可从以下两方面进行探讨:
(1)台站基础信息之间的相关性。搜集17个台站的地质构造概况、地电阻率数据年动态特征、电测深曲线类型及地电观测系统布设等信息,检查是否存在因果关系。相关统计结果(表 2)显示,17个台站在地理地貌、地质构造环境、数据年动态特征、地表水系距离、观测系统线路和电极布设等方面,均存在显著差异,缺乏统一对比性,因此对地电阻率异常的趋势同步变化参考价值有限。
| 表 2 17个台站基础信息 Table 2 Basic information of 17 stations |
(2)中国大陆地区强震与邻近国家大震的相关性。中国大陆主要受太平洋板块向西和印度洋板块向北共同挤压作用影响,其地震活动与周边国家发生的大震呈显著呼应关系,尤以日本大震的影响最为显著。曾小苹等(2014)通过对日本1900—2011年间M 6.9—9.0大震及其后4年中国地区发生的M≥6.0地震的深入研究,发现中国地区的地震普遍滞后于日本地震约0.5—2.0年,且我国新疆、云南、西藏地区与日本大震的对应率位居前三,其他地区也表现出不同程度的关联性。
整理统计2017—2022年中国及其东部临近国家发生的MS≥7.0地震,得到6次地震参数,统计结果见表 3,可知:5次地震发生在2020—2022年(地震目录数据源自中国地震台网中心);除2017年8月8日四川九寨沟MS 7.0地震和2021年5月22日青海玛多县MS 7.4地震,其余4次地震均位于太平洋板块西北缘俯冲条带上,且有3次地震发生在日本,震中均位于日本本州东岸近海,即2011年日本MW 9.0地震余震区,最大地震震级为MS 7.4。
| 表 3 2017—2022年中国及东部临近国家MS≥7.0地震统计 Table 3 Statistics of MS≥7.0 earthquakes in China and neighboring eastern countries from 2017 to 2022 |
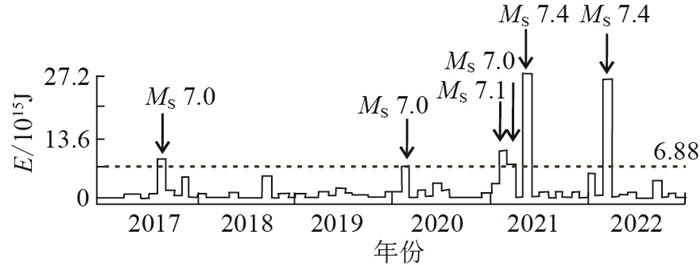
选取中国及其东部临近国家2017—2022年发生的MS≥6.0地震,计算地震释放能量(月值),结果见图 6,可见:6.88×1015 J以上能量均为MS≥7.0地震所贡献,其时序分布与图 4、5中多台地电阻率趋势转折时段基本吻合;尽管2017年有九寨沟MS 7.0地震发生,但多台地电阻率转折不明显,说明该地震释放的能量并未触发异常变化;2021年的玛多MS 7.4地震与之前发生的2次日本地震时间接近,不能准确判断地震对地电阻率趋势的影响。
|
图 6 中国及东部临近国家MS≥6.0地震释放能量分布 Fig.6 Distribution of energy released by the M≥6.0 earthquakes in China and neighboring countries in the east |
综上所述,认为多台地电阻率在2019—2022年间发生的同步趋势转折或扰动变化,可能与太平洋西北缘板块俯冲活动有关。部分台站地电阻率出现趋势转平、转升或者扰动现象,可能与台址电性结构差异所致介质的各向异性变化有关,并不影响地球内部强大应力场变化在不同监测记录中异常信号的产生。该现象与杜学彬(2010)的研究相吻合,即在中国大陆或西北、华北等大区域,同步、近似同步发生的视电阻率长趋势变化的转折或加速异常,或者在长趋势变化过程中发生的下降或上升异常,均属于时空丛集现象,并与中国大陆、大区域的高地震活动水平及其周边远距离大震活动相对应(杜学彬,2010)。
5 结论地电阻率年变周期的影响因素较为复杂,其中气象因素不容忽视。利用多元线性回归方法,对26个台站地电阻率数据进行分析,结果显示,在多数台站中,气温影响系数最大,地下水、气压、降雨量次之。为提取趋势异常,利用傅里叶变换方法进行去年变周期影响,并对部分仍与降雨呈线性关系的数据进行去倾处理,所得地电阻率异常趋势与应力场变化紧密关联,特别是距离较近的蒙城、南京台,地电阻率异常变化可有效反映该区域中等地震异常信号,而多台站广域性异常变化与我国以东太平洋板块西北缘的俯冲活动有关,进而与日本大震的发生呈现出显著的关联性。
沈红会, 叶碧文, 孙春仙, 等. 地电阻率与水位关系的机理分析[J]. 地震, 2020, 40(4): 183-190. |
杜学彬. 在地震预报中的两类视电阻率变化[J]. 中国科学: 地球科学, 2010, 40(10): 1321-1330. |
杜学彬, 孙君嵩, 陈军营. 地震预测中的地电阻率数据处理方法[J]. 地震学报, 2017, 39(4): 531-548. |
钱家栋, 陈有发, 金安忠. 地电阻率方法在地震预报中的应用[M]. 北京: 地震出版社, 1985: 248-255.
|
钱家栋, 曹爱民. 1976年唐山7.8级地震地电阻率和地下水前兆综合物理机制研究[J]. 地震, 1998, 18(Z1): 1-9. |
田山, 郑文俊, 关华平, 等. 地电阻率年变化与气象因素及水位的关系[J]. 地震, 2000, 20(4): 45-49. |
王志贤. 地电阻率年变化的一种物理解释——大柏舍台不同极距地电阻率观测结果[J]. 西北地震学报, 1981, 3(3): 43-47. |
吴忠良. 关于b值应用于地震趋势预测的讨论[J]. 地震学报, 2001, 23(5): 548-551. |
薛靖楠, 李想, 张波, 等. 山东地区b值的统计分析[J]. 华北地震科学, 2011, 29(1): 1-5. |
曾小苹, 林泊宁, 陈维升, 等. 日本大震与中国及邻区中强地震的遥相关[J]. 地球科学(中国地质大学学报), 2014, 39(12): 1864-1872. |
Scholz C H. The frequency-magnitude relation of microfracturing in rock and its relation to earthquakes[J]. Bull Seismol Soc Am, 1968, 58(1): 399-415. |
Wyss M. Towards a physical understanding of the earthquake frequency distribution[J]. Geophys J R Astr Soc, 1973, 31(4): 341-359. |
 2025, Vol. 46
2025, Vol. 46


