2) 中国呼和浩特 010010内蒙古自治区地震局
2) Earthquake Agency of the Nei Monggol Autonomous Region, Hohhot 010010, China
地震仪器监测记录的震动事件包括天然地震和非天然地震,有效识别天然地震和非天然地震事件是监测工作的关键问题(刘莎等,2012)。天然地震主要由地球内部应力变化和能量释放所引发,通过地震记录可深入分析地球内部结构和介质性质,揭示板块构造运动机制、探索地球动力学复杂过程,进而提高地震预测水平。非天然地震主要包括人工爆破、塌陷、矿震等。人工爆破是常见的非天然地震事件,其震源特征与天然地震具有显著差异(曾融生等,2000)。在时频谱特征上,两者存在明显差别,主要体现在持续时长、能量分布以及频带范围等方面(陈银燕,2011;杨千里等,2020)。在地震监测任务中,以往主要依赖经验进行事件类型判别,将不可避免地受到主观因素影响,进而导致误判情况的发生。随着地震台网的不断加密,地震记录的数据量急剧增长,如何快速、准确地判别地震事件类别,正面临前所未有的挑战。
近年来,深度学习技术在地震分类识别领域获得广泛运用。相关研究有:张帆等(2021)利用卷积神经网络,对内蒙古天然地震与爆破事件进行分类,其识别率高达98%;田宵等(2022)利用卷积神经网络,对美国犹他州地震和采石场爆破进行模型训练,识别率达97%。残差网络模型可有效避免网络层次过深导致的梯度弥散和梯度爆炸问题,在图像分类中具有独特优势(He et al,2016)。研究显示,采用基于残差网络模型的地震分类方法,能够精准识别天然地震与人工爆破事件,且识别准确率较高,如:隗永刚等(2019)在首都圈地震与爆炸分类中引入残差网络模型,得到多组对比试验结果,识别率均达97%以上;王梦琪等(2024)提出改进深度残差收缩网络(RSNN)方法,用于地震信号分类识别。
本文基于内蒙古东部及周边地区的天然地震和爆破观测资料,采用短时傅里叶变换,将地震分类问题转换为图像分类问题,并利用残差神经网络构建地震与爆破分类模型,通过训练和测试,评估模型效果和应用价值。
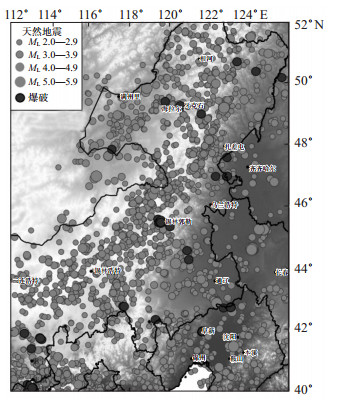
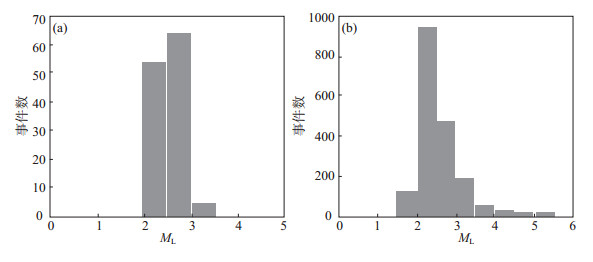
1 数据选取与预处理 1.1 数据选取选取2010—2024年内蒙古东部及周边地区(40°—52°N,112°—126°E)有明确分类的天然地震和爆破事件进行预处理。所选地震和爆破事件空间分布见图 1、震级—频次分布见图 2。其中:①爆破事件167次,震级范围在ML 1.5—3.5,空间分布较为集中,主要发生在采矿区域和几个主要城市或工业区附近;获取单通道记录3 034条。②天然地震事件200次,主要为ML 2.0—3.9地震,遍布整个研究区域,ML≥4.0地震较少且集中分布在特定区域。为了训练样本的平衡,随机选取地震单通道记录3 505条。
|
图 1 研究区域地震和爆破分布 Fig.1 The distribution map of earthquakes and blasts in the study area |
|
图 2 研究区地震和爆破震级—频次分布 (a)爆破;(b)地震 Fig.2 Magnitude-frequency diagram of earthquakes and blasts in the study area |
利用短时傅里叶变换(Short-Time Fourier Transform,STFT),将原始地震信号由时域分布转换成时频分布。STFT是一个二维复函数,表示信号随时间和频率变化的幅度和相位。其离散傅里叶变换(黄苇等,2021)如下
| $ X(m, n)=\sum\nolimits_{k=0}^{N-1} x(k) w(k-n) \mathrm{e}^{-j 2 \mathsf{π} m k / N} $ | (1) |
式中:X(m, n)表示信号在频率m时间n上的幅值;x(k)表示原始信号在时域上的采样值;w(k - n)表示窗函数在(k - n)时刻的值;e-j2πmk/N是复指数项,N为窗口长度;Σ表示对整个离散地震信号进行求和。
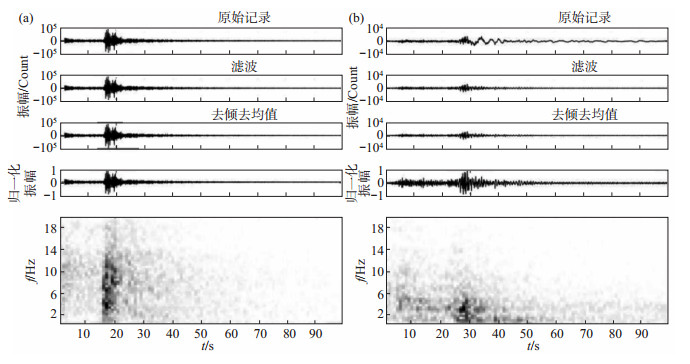
选择震中距200 km以内的数据,每条记录起始点为初至震相前30 s,截取信号长度为100 s的完整震相记录(原始数据采样率为100 Hz),经高通滤波,滤除低频噪声,保留1 Hz以上的信号,进行去趋势化和标准归一化处理,采用短时傅里叶变换(STFT),将震相信号转换为时频域的幅度谱。采用对数变换,在减小数据尺度的同时保持数据内的相对关系,使数据变化相对平滑,缓解模型中的共线性和方差问题(张帆等,2021)。数据转换后得到一个50×49尺寸的时频灰度图像,对应于1—50 Hz频域和0—100 s时间域的对数幅度谱。如:2014年2月8日科尔沁左翼后旗ML 3.3天然地震(震中距127 km),乌兰花(DQL)记录波形见图 3(a);2017年6月29日准格尔旗ML 2.7爆破事件(震中距198 km),大沁塔拉(WLH)记录波形见图 3(b)。由图 3可见,爆破波形中存在一个尾波,其包含更多低频信号,且含有面波成分,而天然地震则显示出更为丰富的频率分布特征。时频谱分析表明,爆炸能量集中在低频成分,地震信号能量则分布在更广泛的频率范围内。
|
图 3 数据处理过程 (a)地震;(b)爆破 Fig.3 Data processing process |
残差网络(Residual Network)是一种特殊的卷积神经网络结构,通过引入残差连接(Residual Connection)和残差学习思想,解决了深度神经网络在训练过程中遇到的梯度消失和梯度爆炸问题,使得深层网络训练变得更加高效(He et al,2016)。
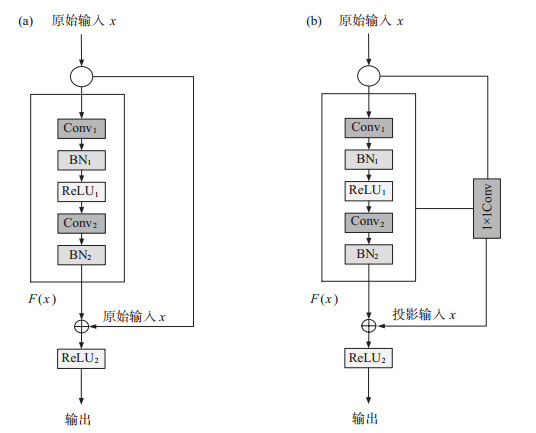
2.1 残差模块选用ResNet18模型(He et al,2016),其残差连接类型包括标准残差连接(Identity Shortcut)与投影残差连接(Projection Shortcut)。如图 4所示,地震数据经预处理,以张量格式作为原始输入信号input x,进入残差模块进行一系列运算,虚线框内的运算涵盖第一层卷积Conv1、批量归一化BN1、ReLU1激活函数、第二层卷积Conv2、批量归一化BN2。输出F(x)信号后,可采取2种运算方式:①原始输入信号input x与输出信号F(x)维度相同,使用标准残差连接,将输入信号x直接传递到输出端,不做任何转换,即通过F(x) + x的方式实现。经第2个ReLU激活函数层,最终输出Output为ReLU2(F(x) + x)。此方法结构简单、计算量小,且不引入额外参数,能够降低过拟合风险。②原始输入信号input x与输出信号F(x)因卷积核变换存在维度不一致现象,引入投影残差连接,通过1×1卷积核进行线性变换(1×1Conv),即使用投影矩阵,将输入信号x投影至与输出信号F(x)相同的维度,得到投影输出Projoutx,进行相加操作,得到F(x) +Projoutx,同样经第2个ReLU激活函数层,输出Output为ReLU2(F(x) +Projoutx)。
|
图 4 2种残差模块 (a) 标准残差连接;(b) 投影残差连接 Fig.4 Two kinds of residual modules |
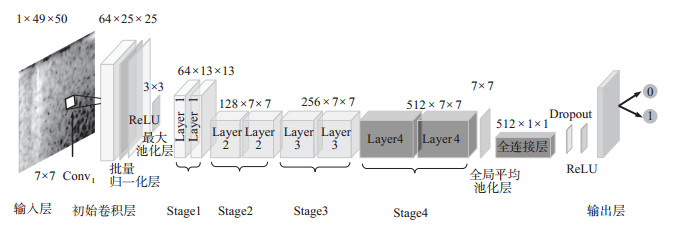
ResNet-18模型网络结构见图 5。ResNet-18模型是一种深度为18层的卷积神经网络,旨在解决网络深度增加时常见的梯度消失和梯度爆炸问题。其结构由输入层、卷积层、多个残差块组、池化层、全连接层组成。输入层数据为经预处理的49×50尺寸的时频域灰度图像,经7×7卷积层、批量归一化、ReLU激活函数和3×3最大池化层处理,降低图像空间维度。ResNet-18模型的核心由多个残差块组成,每个残差块包含2个3×3卷积层,每层后接批量归一化和ReLU激活函数,通过恒等连接将输入直接连接到后续层的输出,允许网络学习输入和输出之间的残差函数。在所有卷积层和残差块处理后,特征图经全局平均池化层展平,通过全连接层,最终通过softmax激活函数,得到图像分类的概率分布。ResNet-18模型设计使其在保持高效计算的同时,能够有效捕捉图像的层次结构特征。ResNet-18模型结构各层参数见表 1。
|
图 5 ResNet-18模型网络结构 Fig.5 Structure diagram of the ResNet-18 network |
| 表 1 ResNet-18网络参数 Table 1 Network parameters of ResNet-18 |
ResNet-18神经网络在训练过程中,使用交叉熵损失函数(潘宇曜等,2023)来度量模型的预测结果与实际标签之间的差异。交叉熵损失函数L计算公式如下
| $ L=-[y \log \overparen{y}+(1-y) \log (1-\overparen{y})] $ | (2) |
式中,y表示输入数据的真实概率,
模型硬件配置如下:CPU为11thGenIntel(R)Core(TM)i7-1195G7,显卡为GeForce MX450。以Anaconda为开发环境,编程语言采用Python 3.11.5,使用Pytorch库搭建残差网络。具体软、硬件配置见表 2。加载ResNet-18预训练模型,优化后超参数见表 3。
| 表 2 模型的软硬件环境配置 Table 2 Configuration of the software and hardware environment for the model |
| 表 3 ResNet网络模型超参数 Table 3 ResNet model hyperparameters |
数据样本总量为6 539条记录,含200次天然地震3 505条单通道记录以及167次人工爆破事件3 034条单通道记录。以4:1的比例将数据样本集划分为训练集与测试集,其中训练集样本5 232条,测试集样本1 307条(天然地震样本608条、人工爆破样本699条)。定义输出标签为“0”的事件是人工爆破,属正例;输出标签为“1”的事件是天然地震,属负例。数据样本分布见表 4。
| 表 4 数据集样本成分 Table 4 Composition of dataset samples |
为了全面评估残差网络性能,综合考虑准确率、精确率、召回率、F1分数、PR曲线和ROC曲线及其曲线下面积(AUC)、损失函数、参数量、计算量以及泛化能力等多个指标,通过多维度评估,更全面了解模型的优缺点,从而选择最优模型。
定义地震数据的测试集样本量为N;TP为真正例,表示预测值为正例且实际也为正例;TN为真负例,表示预测值为负例实际也为负例;FP为假正例,表示预测值为正例但实际为负例(也叫误报);FN为假负例,表示预测值为负例但实际值为正例(也叫漏报)。用Accuracy(准确率)、Precision(精确率)、Recall(召回率)和F1-score(F1分数)、马修斯相关系数(Matthews Correlation Coefficient,简称MCC)对天然地震与人工爆破识别模型性能进行评价。公式如下
| $ \text { Accuracy }=\frac{\mathrm{TP}+\mathrm{TN}}{N} $ | (3) |
| $ \text { Precision }=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FP}} $ | (4) |
| $ \text { Recall }=\frac{\mathrm{TP}}{\mathrm{TP}+\mathrm{FN}} $ | (5) |
| $ \mathrm{F} 1=\frac{2}{\frac{1}{\text { Precision }}+\frac{1}{\text { Recall }}} $ | (6) |
| $ \mathrm{MCC}=\frac{\mathrm{TP} \times \mathrm{TN}-\mathrm{FP} \times \mathrm{FN}}{\sqrt{(\mathrm{TP}+\mathrm{FP}) \times(\mathrm{TP}+\mathrm{FN}) \times(\mathrm{TN}+\mathrm{FP}) \times(\mathrm{TN}+\mathrm{FN})}} $ | (7) |
式中:Accuracy表示正确预测样本数占测试集样本量的比例;Precision表示模型正确预测为正样本数占所有预测为正样本数的比例;Recall表示模型正确预测为正样本数占测试集真实正例样本数的比例;F1-score是精确率和召回率的调和平均值,本模型为二分类。基于MCC数值,可更全面评估模型在类别不平衡问题上的表现。
3.3 评估结果表 5给出ResNet18模型实验结果,可见准确率为98.16%,表明ResNet在整体上对样本的分类更准确。在所有天然地震与人工爆破样本中,ResNet有更好的正确识别能力。ResNet的精确率为99.56%,说明其预测为正类的样本中,实际为正类的比例更高。ResNet的正类召回率约97.02%,表明其在识别所有实际为正的样本方面表现更好。ResNet的F1分数为0.982 9,说明其在精确率和召回率之间取得了更好的平衡。ResNet的MCC为0.961 5,说明其预测与实际标签之间的相关性更强,整体分类性能更好。精确率—召回率曲线(Precision-Recall Curve)用于评估模型在不同阈值下的精确率和召回率。受试者工作特征曲线(Receiver Operating Characteristic Curve)是一种绘制真正例率(TPR)随着假正例率(FPR)变化的图形,用于衡量分类器的准确性与泛化能力。在ROC曲线上,横轴为FPR假正例率(False Positive Rate),是指在所有实际为负例的样本中,被错误判断为正例的比例;纵轴为TPR真正例率(True Positive Rate),是指在所有实际为正例的样本中,被正确判断为正例的比例。AUC(Area Under the Curve)是曲线下的面积,用于量化分类器性能,其取值范围在0—1之间,一般来说,AUC越大,分类器性能越好。
| 表 5 ResNet模型实验结果 Table 5 Experimental results of the ResNet model |
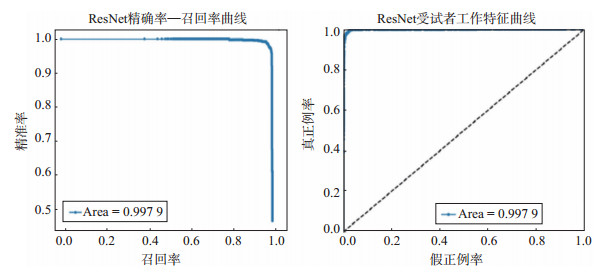
图 6给出PR曲线和ROC曲线,ResNet的PR AUC为0.997 9,表明ResNet在精确率和召回率之间的权衡上表现更好。ResNet的ROC AUC为0.997 7,说明ResNet在区分正负样本方面能力较强。
|
图 6 PR曲线(a)和ROC曲线(b) Fig.6 PR curve (a) and ROC curve (b) |
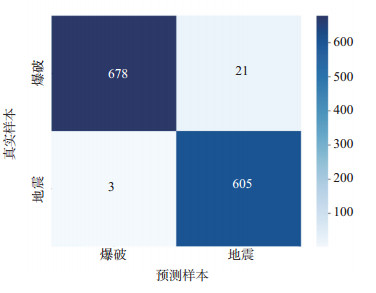
为了直观对比ResNet-18模型对天然地震与人工爆破样本的测试情况,使用二分类混淆矩阵进行分析,如图 7所示,爆破事件为正例,天然地震为负例。每个矩阵含4个单元,单元总和即为测试集样本总量1 307,以横轴方向叠加为爆破真实样本数699和真实地震样本数608,其中:爆破预测正确的数量为678,预测错误的数量为21;地震预测正确的数量为605,预测错误的数量为3。
|
图 7 混淆矩阵 Fig.7 Confusion matrix |
ResNet模型在整个训练过程中显示出更快的损失下降速度,最终达到更低损失值,拟合训练数据方面更为有效。从各项指标来看,ResNet在该任务中的性能优异。具体选择还需根据具体的应用场景和需求来决定。若对精确识别正例的能力要求较高,可能选择ResNet更适合;若对整体平衡性能较为关注,可能需要进一步综合考虑其他因素。
4 结论在2010—2024年内蒙古地震台网观测记录中,将提取的3 505条天然地震和3 034条人工爆破事件单通道记录作为数据集,利用短时傅里叶变换,将地震信号转换为时频灰度图像,作为训练和测试样本,选择ResNet-18残差神经网络进行分类识别。在模型性能方面,ResNet-18在准确率、精确率、召回率、F1分数和马修斯相关系数(MCC)等多个评价指标上均有较好的表现,其中地震与爆炸的分类准确率为98.16%,证实ResNet-18在区分天然地震与人工爆破事件方面具有高效率和高准确度,其中PR AUC和ROC AUC的高值显示了模型良好的泛化能力。将ResNet-18模型应用于实际地震监测系统中,可以实现快速准确的地震事件分类,为地震预警和灾害管理提供有力的技术支持。未来的研究将继续探索不同深度学习模型在地震事件分类任务中的应用,并研究如何结合多源数据来提高分类的准确性和鲁棒性。
文中使用的天然地震和人工爆破数据由内蒙古地震台记录、整理和标注,并进行训练和测试,在此表示感谢。同时,感谢内蒙古自治区地震局提供交流访学机会,感谢同事们的帮助与支持,以及审稿专家在论文完善过程中提出的宝贵意见和建议。
陈银燕. 基于HMM和GMM天然地震与人工爆破识别算法研究[D]. 桂林: 广西师范大学, 2011.
|
黄苇, 周捷, 高利君, 等. 基于同步挤压改进短时傅里叶变换的分频蚂蚁追踪在断裂识别中的应用[J]. 物探与化探, 2021, 45(2): 432-439. |
刘莎, 杨建思, 田宝峰, 等. 首都圈地区爆破、矿塌和天然地震的识别研究[J]. 地震学报, 2012, 34(2): 202-214. |
潘宇曜, 陈焯辉, 林佩欣, 等. 基于ResNet-18网络的桥梁损坏图像分类研究[J]. 科学技术创新, 2023, 11061106(16): 93-96. |
田宵, 汪明军, 张雄, 等. 基于多输入卷积神经网络的天然地震和爆破事件识别[J]. 地球物理学报, 2022, 65(5): 1802-1812. |
王梦琪, 黄汉明, 吴业正, 等. 基于多尺度注意残差网络的地震波形分类研究[J]. 地震工程学报, 2024, 46(3): 724-733. |
隗永刚, 杨千里, 王婷婷, 等. 基于深度学习残差网络模型的地震和爆破识别[J]. 地震学报, 2019, 41(5): 646-657. |
杨千里, 王婷婷, 边银菊. 基于广义S变换的地震与爆炸识别[J]. 地震学报, 2020, 42(5): 613-628. |
曾融生, 陈运泰, 吴忠良. 探测地球内部的"雷达"——地震波(续)[J]. 城市防震减灾, 2000, 3(6): 12-14. |
张帆, 杨晓忠, 吴立飞, 等. 基于短时傅里叶变换和卷积神经网络的地震事件分类[J]. 地震学报, 2021, 43(4): 463-473. |
He K M, Zhang X Y, Ren S Q, et al. Deep residual learning for image recognition[C]//Proceedings of the IEEE conference on computer vision and pattern recognition Las Vegas: IEEE, 2016: 770-778.
|
 2025, Vol. 46
2025, Vol. 46


