随着高速铁路运营时速的不断提升,轨道平顺性已成为保障列车安全性与舒适性的核心指标。TB10754—2018《高速铁路轨道工程施工质量验收标准》(国家铁路局,2019)明确规定,轨道静态铺设的10 m弦长高低偏差限值为2 mm,30 m基线曲率变化率需小于2 mm/5 m。成桥线形作为轨道铺设的基准,其精度直接影响上述指标的实现。然而,成桥线形不仅受实际施工误差的影响,还会因设计阶段对材料时变特性与环境效应的预测偏差而偏离预期(邢子寒等,2022;刘掌红等,2023)。这将导致实际成桥线形偏离设计目标,进而限制道床厚度调整对轨道平顺性的补偿能力(禹壮壮等,2023)。
混凝土徐变与温度梯度效应作为线形长期变化的核心影响因素,其作用机理已较为明晰(曹洪亮等,2020;李志军,2025):徐变源于水泥胶凝体的黏弹性流动,其应变随时间持续累积;温度梯度则通过改变结构内力重分布路径,最终引发跨中下挠速率的非线性增长。然而,现行规范中对徐变效应和温度梯度效应的计算方法存在显著差异,且各计算公式中的影响因素也不尽相同,规范的合理选择将直接影响预拱度设置的科学性。同时,由于实际成桥线形与设计线形所存在的不同程度的误差,可能导致后续轨道铺设无法达到预期(陆粤,2023;舒英杰等,2024)。因此,在轨道铺设前,需基于实际线形重新设计符合轨道平顺性要求的轨道线形。
本文以沈阳至白河铁路某大跨度连续梁桥为研究对象,建立施工全过程仿真模型,系统探讨不同混凝土徐变和竖向温度梯度规范的适用性,并结合线形特征与道床厚度调整限值,提出基于实际成桥线形的轨道线形优化策略,并检验优化后轨道线形的静态铺设高低平顺性。
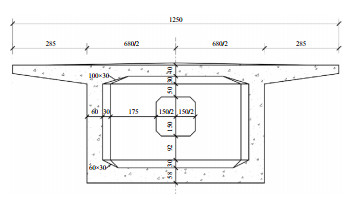
1 工程概况新建沈阳至白河铁路的客运专线某(60+100+60) m连续梁桥,主梁采用单箱单室直腹板形式,跨中截面见图 1。全桥总体立面图见图 2,桥梁全长221.5 m,桥面宽12.5 m,梁高沿纵向圆曲线半径R = 309.666 7 m,中心支点梁高7.5 m,边支点及跨中梁高4.5 m,中跨跨中直线段长10.0 m,边跨直线段长15.75 m,边支座横桥向中心距为5.4 m,中支座横桥向跨中距为5.6 m。连续梁顶板厚度0.4—0.6 m,腹板厚(0.60—0.80 m)—(1.00—1.20 m),底板由跨中的0.58 m按圆曲线变化至根部的1.00 m。箱梁两侧腹板与顶底板相交处均采用圆弧倒角过渡,箱梁悬臂板下设置滴水槽。全梁共设置5道横隔板,边支座处厚度1.5 m,中支座处厚度3.4 m,中跨跨中处厚0.8 m,横隔板处设置检查孔。
|
图 1 连续梁桥跨中截面(单位:cm) Fig.1 Mid-span section of the continuous beam bridge (Unit: cm) |
|
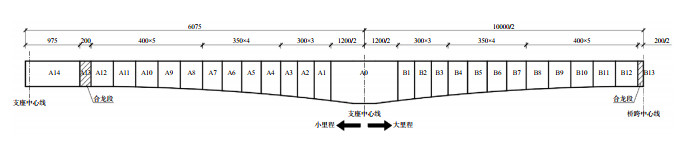
图 2 (60+100+60) m连续梁桥立面图(单位:cm) Fig.2 Elevation view of the (60+100+60) m continuous beam bridge (Unit: cm) |
该连续梁桥采用分节段悬臂浇筑法施工,全桥共分为55个节段,包括0#梁段2段、边跨直线段2段和合拢段3段。浇筑0#块后,沿0#块两侧对称悬浇1#—12#梁段,之后浇筑边跨14#梁段,并浇筑边跨13#梁段完成边跨合龙,浇筑主跨13#梁段完成中跨合龙。0#梁段长12.00 m,边跨直线段长度为9.75 m,边跨合拢段和中跨合拢段长度均为2.00 m(图 2)。
2 典型施工阶段线形仿真分析 2.1 仿真模型建立基于TB 10092—2017《铁路桥涵混凝土结构设计规范》(国家铁路局,2017),考虑自重提高系数、混凝土时变特性、预应力线形、混凝土管道形式、摩阻力及预应力损失等参数,采用Midas Civil建立全桥仿真模型,见图 3。该模型共计131个梁单元、139个节点,成桥阶段全桥支座布置见图 4。全桥梁体采用C55混凝土,纵向预应力钢筋采用Φ15.2钢绞线,材料主要参数见表 1。

|
图 3 全桥仿真模型 Fig.3 Simulation model of the entire bridge |
|
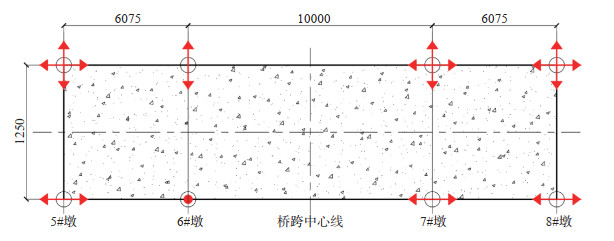
图 4 成桥阶段支座布置(单位:cm) Fig.4 Bearing arrangement at the completion stage of the bridge (Unit: cm) |
| 表 1 材料主要参数 Table 1 Main parameters of materials |
计算荷载时需考虑:①结构自重;②二期恒载,即桥面附属设施,取值为165 kN/m;③预应力荷载,按实际张拉控制应力进行取值;④温度荷载,施工合龙温度按照10 ℃±5 ℃设定,梁体温度按均匀升温25 ℃、降温35 ℃计算;⑤移动荷载,采用ZK铁路列车活载标准(国家铁路局,2017)
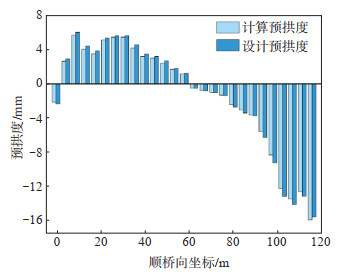
2.2 设计与计算成桥预拱度对比成桥预拱度需考虑恒载及活载的共同作用,一般取恒载与1/2活载所产生的竖向挠度之和。由于桥梁结构和荷载均为对称布置,因此取1/2全桥模型的计算预拱度与设计预拱度进行对比(图 5),可知二者最大相对误差为10.7%,吻合良好,证明建立的仿真模型具有适用性及合理性。
|
图 5 仿真模型与设计资料预拱度对比 Fig.5 Comparison of camber between simulation model and design data |
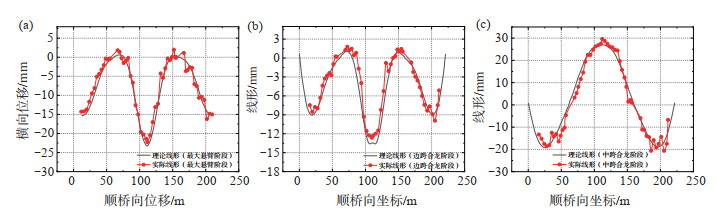
TB 10752—2018《高速铁路桥涵工程施工质量验收标准》(国家铁路局,2019)中规定,连续梁桥线形的总体目标为成桥后梁底线形与设计值误差为-5—15 mm,箱梁轴线误差小于±15 mm。本研究选取最大悬臂阶段、边跨合龙阶段及中跨合龙阶段(成桥阶段)作为典型工况,将实际线形与理论线形进行对比分析,对比结果见图 6。由图 6可见,最大悬臂阶段下,即浇筑并张拉12#块,线形最大绝对误差为4.04 mm,理论悬臂端最大挠度为-23.22 mm,实测为-21.38 mm,相对误差为7.9%;边跨合龙阶段下,线形最大绝对误差为4.00 mm;中跨合龙阶段下,即成桥阶段,线形最大绝对误差为5.58 mm。总体而言,梁体实际线形与理论线形误差较小,满足设计与施工规范要求。
|
图 6 典型施工阶段理论线形与实际线形对比 (a)最大悬臂阶段;(b)边跨合龙阶段;(c)中跨合龙阶段 Fig.6 Comparison of theoretical alignment and actual alignment at typical construction stages |
桥梁结构的长期性能与材料时变行为及环境作用密切相关。其中,混凝土徐变计算方法的理论差异及温度场的非均匀分布对成桥线形的影响机制尚未被充分揭示。前者导致长期挠度的预测值出现偏差,后者则通过非对称热应力改变结构内力重分布路径,进而影响线形演化的长期稳定性。下文将聚焦混凝土徐变与温度梯度效应规范适用性,系统量化不同规范方法对成桥线形的影响,为全寿命周期线形控制提供更完备的理论框架。
3.1 混凝土徐变 3.1.1 徐变系数计算方法目前,国内外混凝土桥梁设计现行规范主要有:美国ACI(ACI Committee,1992)、欧洲CEB2010(Comite Euro-International Du Beton,2013)、中国JTG 3362—2018《公路钢筋混凝土及预应力混凝土桥涵设计规范》(中华人民共和国交通运输部,2018)(下文简称“中交18”规范)和TB 10092—2017《铁路桥涵混凝土结构设计规范》(国家铁路局,2017)(下文简称“中铁17”规范)。表 2列出上述规范给出的混凝土徐变系数计算公式及适用条件。
| 表 2 各规范徐变系数公式及其适用条件 Table 2 Creep coefficient formulas and their applicable conditions in various standards |
每一节段接缝处张拉后高程和成桥后高程之间的差值,不仅受到施工过程的影响,还主要受到混凝土徐变、环境温度的影响。为评估不同规范的适用性,设定仿真模型中除混凝土徐变以外的其余参数均相同,其中竖向温度梯度采用中国JTG D60—2015《公路桥涵通用设计规范》(中华人民共和国交通部,2015)的规定。
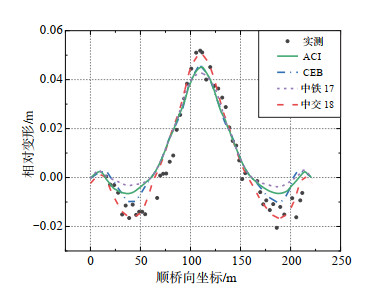
以每一节段接缝处张拉后线形和成桥后线形[图 6(c)中实测线形]之间的差值为实测值,与理论相对变形进行对比,理论相对变形为不同规范计算得到的徐变变形与中公15规范所得温度效应变形之和,结果见图 7、表 3。可见,实测相对变形上挠最大值为0.052 m,下挠最大值为-0.021 m,各规范中徐变变形曲线趋势大致相同,但幅度不一。通过比较理论值与实测值的均方误差,发现使用中交18规范计算出的徐变变形与实测值的吻合度最高,其后依次为CEB规范、ACI规范、中铁17规范。可见,对于本研究依托工程而言,中交18规范在混凝土徐变预测方面更具适用性。
|
图 7 相对变形实测值与徐变规范理论值对比 Fig.7 Comparison of measured relative deformation and theoretical values from creep standards |
| 表 3 相对变形均方误差 Table 3 Mean square error of relative deformation |
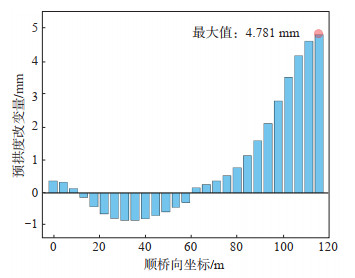
混凝土长期收缩徐变引起的时变变形累积对预拱度的动态影响需进一步量化。为此,分别构建考虑和忽略10年收缩徐变效应的2种模型,对比分析预拱度设置值的差异,预拱度改变值见图 8。可见,当忽略10年收缩徐变效应后,跨中梁段预拱度增大,边跨梁段预拱度减小,改变量的最大值为4.781 mm。
|
图 8 混凝土长期收缩徐变效应对预拱度改变量 Fig.8 Effect of long-term shrinkage and creep of concrete on the change in camber |
混凝土收缩徐变将导致跨中持续下挠,进而影响轨道的平顺性。若忽略混凝土收缩徐变对预拱度的影响,将导致结构性能的系统性偏差,这种偏差在桥梁全寿命周期内呈现渐进式累积特征。因此,在设定预拱度时,必须充分考虑混凝土的长期收缩徐变影响。
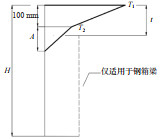
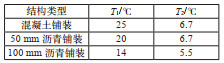
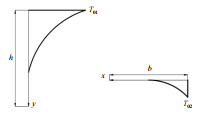
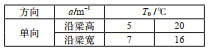
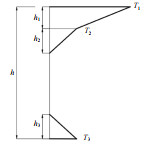
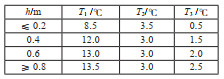
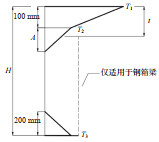
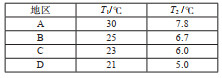
3.2 温度梯度 3.2.1 竖向温度梯度计算方法目前,国内外关于竖向温度梯度的现行规范有:中国JTG D60—2015《公路桥涵通用设计规范》(中华人民共和国交通部,2015)(下文简称“中公15”规范)、中铁17规范、英国BS5400规范(British Standards Institution,1978)、美国AASHTO规范。表 4列出上述规范给出的竖向温度梯度示意图及相关规定。
| 表 4 各规范竖向温度梯度规定 Table 4 Vertical temperature gradient specifications in various standards |
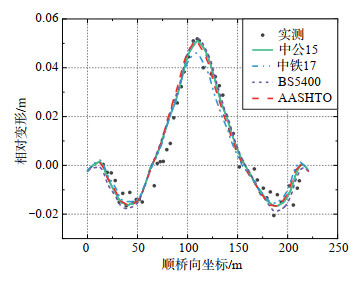
为评估不同规范的适用性,设定仿真模型中除竖向温度梯度以外的其余参数均相同,其中混凝土徐变采用中交18规范计算。与3.1.2节相似,仍以每一节段接缝处张拉后线形和成桥后线形[图 6(c)中实测线形]之间的差值为实测值,与理论相对变形进行对比,理论相对变形为不同规范计算得到的温度效应变形与中交18规范所得徐变变形之和,结果见图 9、表 5。
|
图 9 相对变形实测值与温度规范理论值对比 Fig.9 Comparison of measured relative deformation and theoretical values from temperature standards |
| 表 5 相对变形均方误差 Table 5 Mean square error of relative deformation |
由图 9、表 5可知,通过比较理论值与实测值的均方误差,发现使用中公15规范计算所得徐变变形与实测值的吻合度最高,其后依次为AASHTO规范、中铁17规范、BS5400规范。可见,对于本研究依托工程而言,中公15规范在温度效应预测方面更具适用性。
4 基于成桥线形的轨道静态不平顺分析 4.1 优化轨道线形在2.3节中,通过梁体实际线形与理论线形的比较,初步判断桥梁线形满足设计与施工规范要求。为使后续轨道静态铺设平顺性满足限值要求,需进一步以实际线形为基准线形,结合线形特征及桥上道床厚度可调整能力,得到满足静态验收要求的优化轨道线形。参考舒英杰等(2024)的研究方法,结合傅里叶级数特点,假设优化后的主梁纵断面为函数R(x),可表示为
| $ R(x)=a_0+\sum\nolimits_{k=1}^N\left[a_k \cos (k \omega x)+b_k \sin (k \omega x)\right] $ | (1) |
式中:x为线路里程组成的向量,
以最大离心加速度为优化目标,以线路纵断面端部坡度、道床厚度限值为约束条件,构建基于成桥线形的轨道线形优化函数(舒英杰等,2024)。即:
| $ \begin{array}{l} \min \max\limits_i\left|A_{\mathrm{LX}}\left(x_i\right)\right| \\ \text { s.t. } \mathrm{sp}_1 \leqslant \frac{R\left(x_n\right)-R\left(x_{n-1}\right)}{x_n-x_{n-1}} \leqslant \mathrm{sp}_2 \end{array} $ | (2) |
| $ \begin{array}{l} \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;T_1 \leqslant R\left(x_i\right)-B\left(x_i\right) \leqslant T_2 \quad \forall x_i \in x \\ A_{\mathrm{LX}}\left(x_i\right)=V^2 \cdot\left|\frac{\arctan \frac{R\left(x_{i+2}\right)-R\left(x_i\right)}{x_{i+2}-x_i}-\arctan \frac{R\left(x_{i+1}\right)-R\left(x_{i-1}\right)}{x_{i+1}-x_{i-1}}}{\sqrt{\left(x_{i+1}-x_i\right)^2+\left(R\left(x_{i+1}\right)-R\left(x_{i-1}\right)\right)^2}}\right| \end{array} $ | (3) |
式中,sp1、sp2为线路纵断面端部坡度限值,T1、T2为道床厚度限值,B(xi)为里程xi处的实测主梁高程,ALX(xi)为里程xi处离心加速度。
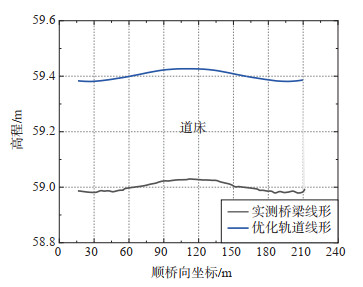
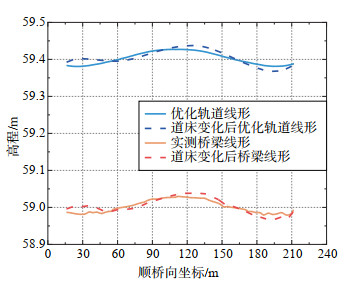
同时,由于轨道线形优化是通过调整道床厚度来实现的,而道床厚度的改变将会使得桥梁发生二次变形,因此需将此变形叠加至轨道高程,并进一步判断该轨道线形是否满足平顺性要求。沿顺桥方向,计算道床厚度变化量,将重量变化等效为均布荷载。图 10、图 11分别为优化后轨道线形和道床厚度改变后桥梁线形和轨道线形,可见:①图 10中,实测桥梁线形曲线与优化轨道线形曲线间为预估铺设道床,其厚度满足330—450 mm的范围要求,且优化后轨道线形呈圆顺趋势特点,并大致符合桥梁线形趋势;②图 11中,道床厚度改变使得5#墩、6#墩之间边跨出现上挠,7#墩、8#墩之间边跨出现下挠,主跨主要出现上挠。全桥范围内,最大上挠为17.445 mm,最大下挠为11.994 mm。
|
图 10 实测成桥线形优化效果 Fig.10 Optimization effect of the measured bridge alignment |
|
图 11 道床厚度改变后的线形 Fig.11 Alignment after adjustment of ballast thickness |
静态铺设轨道高低平顺性由轨道矢高偏差值决定。根据TB10754—2018《高速铁路轨道工程施工质量验收标准》(国家铁路局,2019),其限值应符合表 6所列要求。
| 表 6 轨道静态铺设规定 Table 6 Specifications for static track laying |
对二次变形后的优化轨道线形进行静态不平顺评价。基于30 m弦测法,测得短波不平顺最大值为1.61 mm/5 m,符合规范中不超过2 mm/5 m(表 6)的规定,表明轨道线形平顺性良好。即表明,基于本研究依托工程的实际成桥线形,可以得到平顺性良好的轨道线形。
5 结论通过理论分析与工程实践相结合,系统探讨了不同规范中混凝土徐变和竖向温度梯度对高速铁路大跨度连续梁桥线形的影响,并提出基于实际成桥线形的轨道线形优化方法。研究得出以下结论:
(1)各典型施工工况下,中跨合龙阶段(成桥阶段)的理论线形与实际线形的绝对误差最大值为5.58 mm,吻合良好,满足设计与施工规范要求。
(2)混凝土徐变和温度梯度效应预测中,中交18规范和中公15规范所得相对变形与实测变形的均方误差最小,为2.54×10-5,表明对于本研究依托工程而言,中交18规范对混凝土徐变变形的预测更为准确,中公15规范对温度效应变形的预测更为准确。
(3)基于成桥线形特征与道床厚度可调能力,得到优化后的轨道线形。在考虑了道床厚度变化造成的二次变形后,轨道线形的短波不平顺最大值为1.61 mm/5 m,低于静态铺设高低平顺性2 mm/5 m的限值,表明本研究依托工程中实际成桥线形可满足后续轨道铺设要求。
曹洪亮, 陈亮, 姜竹昌, 等. 钢-混组合连续箱梁施工预拱度设置影响因素研究[J]. 世界桥梁, 2020, 48(3): 53-57. |
国家铁路局. TB/T 3466—2016铁路列车荷载图式[S]. 北京: 中国铁道出版社, 2017.
|
国家铁路局. TB10092—2017铁路桥涵混凝土结构设计规范[S]. 北京: 中国铁道出版社, 2017.
|
国家铁路局. TB10754—2018高速铁路轨道工程施工质量验收标准(2023年局部修订)[S]. 北京: 中国铁道出版社, 2019.
|
国家铁路局. TB10752—2018高速铁路桥涵工程施工质量验收标准[S]. 北京: 中国铁道出版社, 2019.
|
李志军. 波形钢腹板PC箱形组合梁施工过程线形和应力的分析和监控[J]. 公路, 2025, 70(2): 142-147. |
刘掌红, 崔冰, 阳逸鸣, 等. C60低收缩低徐变高性能混凝土收缩徐变行为试验研究[J]. 混凝土, 2023(6): 163-167. |
陆粤. 基于行车品质的大跨度铁路桥梁成桥线形评价方法研究[D]. 成都: 西南交通大学, 2023.
|
舒英杰, 王铭, 陆粤, 等. 基于车体加速度的超大跨度桥上线路纵断面优化方法[J]. 铁道标准设计, 2024, 68(4): 35-41. |
邢子寒, 刘永健, 闫新凯, 等. 不同截面形式混凝土梁桥的竖向温度梯度效应分析[J]. 建筑科学与工程学报, 2022, 39(2): 97-110. |
禹壮壮, 舒英杰, 陆粤, 等. 基于成桥施工偏差的大跨度铁路桥梁线路纵断面设计适应性分析[J]. 铁道标准设计, 2023, 67(3): 61-67. |
中国人民共和国住房和城乡建设部. GB50010—2010混凝土结构设计规范[S]. 北京: 中国建筑工业出版社, 2010.
|
中华人民共和国交通运输部. JTG 3362—2018公路钢筋混凝土及预应力混凝土桥涵设计规范[S]. 北京: 人民交通出版社, 2018.
|
中华人民共和国交通运输部. JTG D60—2015公路桥涵设计通用规范[S]. 北京: 中国铁道出版社, 2015.
|
ACI Committee. ACI 209 R-92 Prediction of Creep, Shrinkage and Temperature Effects in Concrete Structures[S]. Detroit: American Concrete Institute, 1992.
|
Comite Euro-International Du Beton. CEB-FIB Model Code 2010[S]. Lausanne: Ernst & Sohn GmbH & Co. KG, 2013.
|
British Standards Institution. BS 5400-2: 1978 Steel, concrete and composite bridges, Part 2. Specification for Loads: BS5400 Steel[S]. British Standards Institution, 1978.
|
 2025, Vol. 46
2025, Vol. 46