2) 中国呼和浩特 010010 内蒙古地震台;
3) 中国呼和浩特 010010 内蒙古自治区地震局
2) The Nei Monggol Earthquake Station, Hohhot 010010, China;
3) Earthquake Agency of the Nei Monggol Autonomous Region, Hohhot 010010, China
天然地震通常由地壳板块移动、断层滑动、火山活动等自然地质过程引起,这些过程导致地壳积累的应力在断层上释放而产生地震波。人工爆破通常由炸药等爆炸物的化学反应引起。爆炸产生的能量以震动形式向四周传播,形成地震波,这种震源是人为的、瞬时的,与地震的应力释放机制不同。爆破时介质在剪应力和拉应力作用下产生裂隙,剩余一部分能量以波的形式传播到地面,引起地面质点的振动,形成爆破地震(陈润航等,2019)。另外,一般人工爆炸发生在近地表,而构造地震震源较深。由于震源机制、深度的差异,天然地震与人工爆炸地震记录在幅值衰减、能量分配、高低频成分等均有所不同。地震与爆炸的识别研究起源于对核爆炸的监测,其目的是为了区分核爆炸引起的地震波与构造地震波。随着研究的不断深入,科研人员利用多种判据对人工爆破和天然地震进行甄别,如震源位置、震源深度、P波初动、P波与S波最大振幅比、体波震级与面波震级比、倒谱、瞬态谱等(王婷婷等,2011),并且随着模式识别和机器学习的发展,已有多种人工智能方法被应用于该领域。如:边银菊(2002)建立遗传BP神经网络,用来识别爆破和地震;安镇文等(2008)借助量子场论和相变理论分析了地震波波长与动量间的关系;黄汉明等(2010)利用v-SVC支持向量分类机,对波形记录获取的香农熵特征和不同信号窗长进行识别检验;陈晓琳等(2019)采用主成分分析方法,提取出与震级相关的震前异常作为输入变量,建立支持向量机回归的震级预测模型;范晓易等(2020)采用支持向量机LIBSVM方法,对地震事件进行分类识别;蔡杏辉等(2020)利用离散小波变换和小波包变换对地震信号进行分解,并采用BP神经网络进行识别。本文采用小波函数,对内蒙古西部地区地震、爆破事件进行小波变换,并使用支持向量机和BP神经网络方法构建分类模型,旨在有效识别地震和爆破事件。
1 研究方法 1.1 小波变换鉴于传统傅里叶变换在处理非平稳信号时的缺陷,研究人员将整个信号分解为多个平稳的小信号进行分析处理,此即为短时傅里叶变换。然而,短时傅里叶变换也存在局限性,无法适用于非稳态变化信号。为此引入小波变换,将傅里叶变换的基函数替换为有限长度且会衰减的小波基,便可处理非稳态变化信号。
(1)利用离散小波(Discrete Wavelet Transform,DWT)能将信号分解成不同频率的小波分量,从而提取信号的局部时频信息。公式如下
| $ \mathrm{WT}_f(m, k)=\left\langle f(t), \varPsi_{m k}(t)\right\rangle=2^{-m / 2} \int_R f(t) \varPsi \cdot\left(2^{-m} t-k\right) \mathrm{d} t $ | (1) |
其中:
(2)静止小波变换(Stationary Wavelet Transform,SWT)是在进行每一层变换时对所使用的高通、低通滤波器进行采样。由SWT得到的A、D长度均相同。
(3)小波包分解(Wavelet Packet Transform,WPT)是小波变换的一种变体,是将信号分解成1组具有不同频带的子带,从而更准确地捕获信号的局部特征。
1.2 特征参数 1.2.1 能量比EWT假设S是原始信号,长度为1,则Sj为原始信号分解后的第j个小波系数,经DWT、SWT分析变换后,将近似系数、细节系数按序排列,进行小波包分解(Wavelet Packet Transform,WPT),将最后1层分解后的系数按小波数节点的顺序排列,长度为c,则能量比EWT表示为
| $ E_{\mathrm{WT}}(j)_{100^*}=\frac{\sum_{k=1}^c S_{(j, k)}^2}{\sum_{i=1}^l S_i^2} $ | (2) |
假设S为原始信号,则Si是原始信号在任意1组正交基上的第i项系数。E表示熵,则E是每个正交基系数变换的叠加值,即
| $ E_{\text {shannon }}(i)=-\sum_{j=1}^c S_{(i, j)}^2 \lg \left[S_{(i, j)}^2\right] $ | (3) |
| $ E_{\lg }(i)=\sum_{j=1}^c \lg S_{(i, j)}^2 $ | (4) |
支持向量机(support vector machines,SVM)是一种强大的监督学习算法,在地学研究领域中应用广泛(唐淑兰等,2023)。它通过寻找最大间隔超平面实现良好的分类效果,其核心思想是最大化2个类别之间的间隔,从而提高模型的泛化能力。通过引入核函数,支持向量机可以处理非线性分类问题。支持向量是距超平面最近的数据点,它们决定了超平面的位置。支持向量满足以下条件
| $ y_i\left(w \cdot x_i+b\right)=1 $ | (5) |
式中,yi为数据点xi的类别标签,取值为1或-1。
1.4 BP神经网络BP神经网络是一种按误差反向传播训练的多层前馈网络,简称为BP算法。其基本思想是,基于梯度下降策略,以目标的负梯度方向对参数进行调整,使网络的实际输出值和期望输出值的误差为最小。其主要特点是:信号正向传播,而误差反向传播。而且,BP神经网络可以应用在地震滑坡危险性预测研究、地震模拟振动台多参量优化控制、地震噪声波形检测(巫立华等,2021)等方面,是一种实用算法。
2 数据选取选取巴彦淖尔地震监测中心站下辖的乌加河测震台、乌力吉测震台、策克测震台2020—2023年记录的内蒙古西部地区爆破事件波形,并与同期该区天然地震波形统一进行分类归纳,其中2类事件的震级均大于1、震中距均小于300 km,从中筛选得到垂直(BHZ)分量记录清晰且信噪比高的各100次事件,并分别选择80条单台记录数据用作训练样本,并将剩余的共40个单台记录用作测试样本。所选地震事件和爆破事件分布见图 1。

|
图 1 内蒙古自治区西部地区地震事件、爆破事件分布 Fig.1 Distribution map of earthquake and blasting events in western Nei Monggol |
利用小波变换对所选事件进行分解,具体流程如下:①使用MSDP软件(测震分析软件,具备震相分析、地震定位、地震编目、提交数据库、归档等功能),将事件导出为ASCII格式。②使用Matlab程序编写小波变换分解程序,实现对事件的DWT、SWT、WPT分解。图 2—图 4分别给出对地震、爆破事件的DWT、SWT、WPT分解实例。③将其各自系数的能量比、香浓熵、能量熵进行单独、两两组合、全部组合后作为特征参数。

|
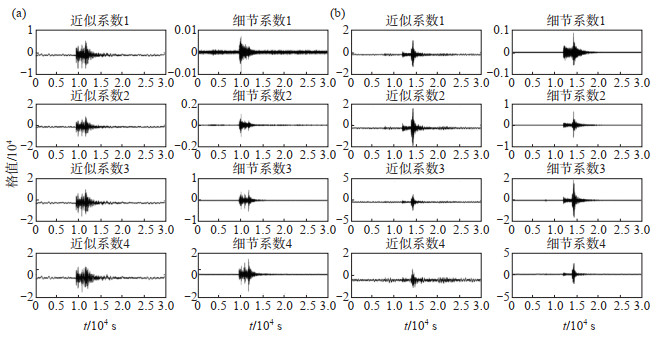
图 2 利用DWT对爆破事件(a)、天然地震事件(b)的分解(db4) (a) 爆破;(b) 天然地震 Fig.2 Decomposition of blasting and natural earthquake events by DWT (db4) |
|
图 3 利用SWT对爆破事件(a)、天然地震事件(b)的分解(db4) (a) 爆破;(b) 天然地震 Fig.3 SWT decomposition of blasting and natural earthquake events (db4) |
|
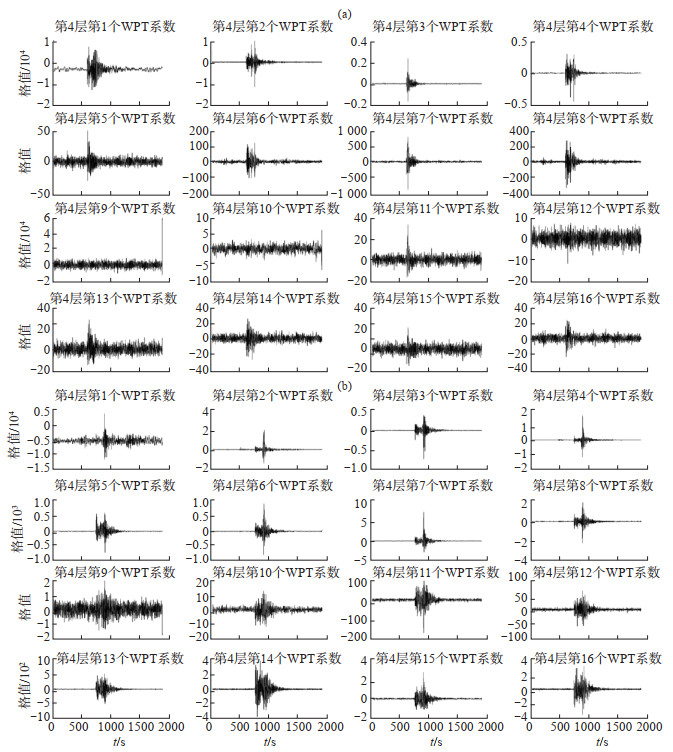
图 4 利用WPT对爆破事件(a)、天然地震事件(b)的分解(db4) Fig.4 Decomposition of blasting and natural earthquake events by WPT (db4) |
与标准傅里叶变换相比,小波分析所使用的小波函数具有不唯一性,满足小波容许条件的函数均可作为小波函数。通常,采用不同小波函数来分析同一问题会产生不同结果,凸显了小波函数选取的重要性。因此,在选取小波函数时,主要应遵循以下原则。
(1)自相似性原则。若选择的小波函数与信号具有一定相似性,则变换后能量将更加集中,从而可以有效减少计算量。
(2)支撑长度。小波函数Ψ(t)、Ψ(ω)及尺度函数φ(t)、φ(ω)的支撑区间,是当时间或频率趋向于无穷大时,Ψ(t)、Ψ(ω)、φ(t)、φ(ω)从1个有限值收敛到0的长度。因为支撑长度太长会产生边界问题,支撑长度太短消失矩太低,不利于信号能量的集中,故选择支撑长度为5—9的小波(魏明果,2005)。
(3)对称性。图像处理中有利于避免移相。
因此,遵循以上原则,选择db7\sym6\rbiol1.5小波基函数。首先,对测震台站观测数据(数据长度2 000 s)按照db7、rbiol1.5、sym6进行DWT、SWT、WPT分解,得到DWT 15维特征向量、SWT 24维特征向量、WPT 48维特征向量;然后,分别计算其能量比、香浓熵、能量熵,并利用构造函数,得出特征参数;最后采用SVM、BP神经网络进行识别。
3.3 波形分类及检验效果为了有效识别爆破和天然地震事件,设定以下参数并进行结果分析。
(1)具体实验参数。①小波基函数为db7小波、sym6小波、rbiol.5小波。②支持向量机类型:C-Support Vector Classification(C-SVC)和v-Support Vector Classification(v-SVC)。③核函数:线形核、多项式核、经向基核、Sigmoid核。
(2)BP参数。①输入节点:特征向量维数。②隐层数量:
分别利用3种小波分解方式、3种小波基函数提取特征参数能量比、香农熵、能量熵,采用2种支持向量机和4种核函数的随机组合,共进行多组识别实验,每组实验都对40个测试数据进行识别,最后统计识别准确率。前4种识别最优解见表 1,测试结果见图 5。分析表明,“DWT + db7 +能量比+香农熵+能量熵+ v-SVC +线性核”识别率最高,为95%。
| 表 1 支持向量机识别最优解 Table 1 Optimal solution of support vector machine |
|
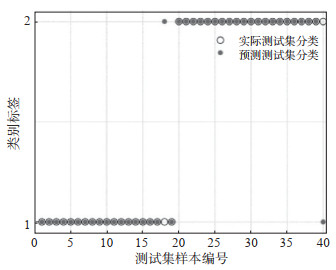
图 5 测试集的实际分类和预测分类类别标签1为天然地震事件;标签2为爆破事件 Fig.5 Actual classification and predictive classification diagram of the test dataset |
利用不同小波分解方式、小波基函数提取特征参数能量比、香农熵、能量熵与构建的BP神经网络模型和参数的随机组合,进行多组识别实验,每组实验都对40个测试数据进行识别,最后统计识别准确率。其中前4种识别最优解见表 2,测试结果见图 6。分析表明,“DWT + db7 +能量比+香农熵+能量熵”在BP神经网络模型中识别率最高,为93%。
| 表 2 BP神经网络识别最优解 Table 2 Optimal recognition effect of BP neural network |
|
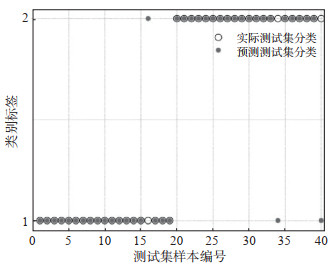
图 6 测试集的实际分类和预测分类类别标签1为天然地震事件;标签2为爆破事件 Fig.6 Actual classification and predictive classification diagram of the test dataset |
为了对比不同方法分类模型的分类效果,在使用支持向量机、BP神经网络时,所采用的地震数据前期处理方式相同,对于随机挑选的地震所算出的参数也是相同的,对于2种识别方式的特征向量,均按照能量比、香浓熵、能量熵单独、两两组合及3个一起组合的方式进行实验,最终支持向量机实验288组,BP神经网络实验96组。由实验结果可知,支持向量机在采用“DWT + db7 +能量比+香农熵+能量熵+ v-SVC +线性核”组合实验中识别准确率最高,为95%,而BP神经网络在实验中最高识别准确率为93%,显然没有支持向量机识别率高,故支持向量机更适用于本研究所用到的数据集。
BP神经网络可优化目标使经验风险最小化,但易陷入局部最优而导致训练结果与支持向量机(SVM)不一致。SVM每一步都有严格的理论和数学推导,其基于结构最小化风险,泛化能力强于BP神经网络,算法成熟,而且具有较强的逼近能力。
本文采用支持向量机、BP神经网络方法进行了地震和爆破事件的识别实验,因塌陷事件记录较少,未进行3类事件的识别研究。今后将尽量收集更多其他非天然地震事件,深入开展相关研究。
安镇文, 郭祥云, 边银菊, 等. 核爆炸与地震识别研究进展[J]. 国际地震动态, 2008(8): 22-31. DOI:10.3969/j.issn.0253-4975.2008.08.003 |
边银菊. 遗传BP网络在地震和爆破识别中的应用[J]. 地震学报, 2002, 24(5): 516-524. DOI:10.3321/j.issn:0253-3782.2002.05.009 |
蔡杏辉, 张燕明, 陈惠芳, 等. 基于小波特征和神经网络的天然地震与人工爆破自动识别[J]. 大地测量与地球动力学, 2020, 40(6): 634-639. |
陈润航, 黄汉明, 施佳朋, 等. 天然地震与人工爆破地震波形的实时分类研究[J]. 地球物理学进展, 2019, 34(5): 1 721-1 727. |
陈晓琳, 李盛乐, 刘小利, 等. 基于支持向量机回归的震例挖掘分析[J]. 大地测量与地球动力学, 2019, 39(Z1): 88-92. |
范晓易, 曲均浩, 刘方斌, 等. 使用支持向量机识别地震类型的影响因素分析[J]. 大地测量与地球动力学, 2020, 40(10): 1 034-1 038. |
黄汉明, 边银菊, 卢世军, 等. v-SVC算法在地震与爆破识别及窗长度选取中的应用[J]. 地震地磁观测与研究, 2010, 31(3): 24-31. |
唐淑兰, 孟勇. 结合小波变换、SVM和投票法的ASTER影像岩性分类——以东天山尾亚地区为例[J]. 遥感学报, 2023, 27(7): 1 702-1 712. |
王禄军, 尹战军, 翟浩, 等. 基于支持向量机的内蒙古地区台网天然地震与人工爆破的自动识别与分析[J]. 大地测量与地球动力学, 2022, 42(3): 326-330. |
王婷婷, 边银菊. 识别天然地震和人工爆破的判据选择[J]. 地震地磁观测与研究, 2011, 32(6): 62-67. |
魏明果. 实用小波分析[M]. 北京: 北京理工大学出版社, 2005.
|
巫立华, 张宝剑, 林彬华, 等. BP神经网络在地震噪声波形检测中的应用[J]. 华南地震, 2021, 41(3): 116-121. |
 2025, Vol. 46
2025, Vol. 46

