2. 中国黑龙江 154101 鹤岗地震台;
3. 中国黑龙江 154101 鹤岗市自然资源局;
4. 中国北京 100081 中国地震局地球物理研究所
2. Hegang Seismic Station, Heilongjiang Province 154101, China;
3. Hegang Natural Resources Bureau, Heilongjiang Province 154101, China;
4. Institute of Geophysics, China Earthquake Administration, Beijing 100081, China
为了提升我国对全球微小地震的监测能力,中国地震局“一带一路”项目拟在黑龙江鹤岗建设小孔径地震台阵。按照项目初步设计,黑龙江省地震局在鹤岗市郊区三道林场备选场地开展2期仪器勘选工作。勘选场地是否满足建设要求,是施工前亟待认清的问题。在台阵勘选期间记录到多次矿震和天然地震。理论上,在震源参数、传播路径、观测仪器等因素相同前提下,各子台记录的地震波形和频谱特征应具有高度相关性和一致性。波形和频谱特征的一致性可作为勘选场地适合建设台阵的依据之一。考虑到勘选时间较短,记录地震数较少,无法采用大量震例进行分析,因此选用典型矿震和天然地震事件,与已有研究成果对比,通过分析各子台频谱特征及一致性对勘选场地进行评估,并在此基础上,分析典型矿震和天然地震时频特征的异同点。识别矿震和天然地震的方法较多(刘莎等,2012;王风等,2013;郑建常等,2014),其中短周期面波是否发育是识别二者的一个明显特征(和雪松等,2006)。本文基于台阵的多子台数据,依据矿震面波发育的特征,采用希尔伯特—黄变换(Hilbert-Huang Transform,简写为HHT)方法,通过EMD分解和Hilbert谱分析,比较矿震和天然地震时频特征异同。
1 研究方法分析信号的频谱特征,通常采用传统傅里叶变换(FFT)方法,然而FFT从时间域转换到频率域后,会丢失时间信息,无法确定频率出现和消失的时刻。时频分析技术是分析频谱随时间变化的有效工具,弥补了以上不足。常用的时频分析方法有短时傅里叶变换(STFT)、Gabor变换、Wigner-Viller等(万永革,2012),但这些方法实际上只在理论上能处理非线性非平稳信号。不同于传统方法,HHT彻底摆脱了线性和平稳性的束缚,适用于分析非线性非平稳信号,如地震波信号。
HHT假设任何复杂信号均是由独立的本征模态函数(IMF)所组成,每个模态既可以是线性和平稳的,也可以是非线性和非平稳的。在整个信号时间段内,一个IMF最终需要满足2个条件:①信号中极值点的数目与过零点的数目相等或者最多相差一个;②信号极大值点构成的上包络与极小值构成的下包络关于时间轴对称。利用经验模态分解(EMD),可将待分析信号分解为多个IMF叠加的形式,分解出来的IMF分量包含原信号不同时间尺度的局部特征信息,时间尺度定义为相邻极值点的时间跨度。由此可见,HHT仅依据数据自身时间尺度即可进行信号分解,无须预先设定任何基函数,也不受Heisenberg测不准原理制约,因此在时间域和频率域同时可达较高精度,适合突变信号分析(武安绪等,2005;张义平等,2005;杨培杰等,2007;戴勇等,2017)。
EMD分解后对每一个IMF进行Hilbert变换,得到相应的Hilbert谱,将每个IMF标示在联合时频域中,汇总所有IMF的Hilbert谱即可得到原始信号的Hilbert谱,它是一个时间—频率—能量三维分布图像。
Huang等(1998)在定义Hibert谱的同时定义了边际谱,即对希尔伯特谱在时间上进行积分,公式如下
| $h\left(\omega \right) = \int_0^T {H\left({\omega, t} \right)} {\rm{d}}t$ | (1) |
从统计观点上看,边际谱表示该频率值的振幅在时间上的求和,反映了各频率点的能量分布,其意义与傅里叶变换的频谱完全不同。在传统的傅里叶分析中,频率被定义为有恒定幅度的完整的正弦(余弦)波形,其持续时间是无限的,因此至少需要一个完整的正弦(余弦)波形来定义局部频率的值。傅里叶频谱的幅值只能反映频率在信号中存在的可能性大小,而边际谱的幅值则是反映频率在信号中的真实存在,是信号中某一频率在各个时刻的幅值之和(钟佑明,2004;黄光南等,2009;梁宏等,2019)。
2 观测资料及处理观测资料采用鹤岗三道林场地震台阵2次勘选数据。该台阵设计为NORESS同心圆型,由1个中心点、4个环组成,共布设25个子台(包含中心点子台,图 1)。由内到外各环子台数为1、3、5、7、9,且环上站点均匀分布,以保证测定来自各个方向的地震事件的方位角和慢度。第一次勘选时间段为2019年5月11日—24日(14天),共布设9个子台,分别为:sdzx、sd1-2、sd2-5、sd3-2、sd3-4、sd3-6、sd4-3、sd4-6、sd4-9。第二次勘选时间段为2019年8月3日—9月4日(31天),共布设15个子台,分别为:sd1-1、sd1-3、sd2-1、sd2-2、sd2-4、sd3-1、sd3-3、sd3-5、sd3-6、sd3-7、sd4-1、sd4-4、sd4-5、sd4-7、sd4-8。勘址使用以下仪器:CMG-3T宽频带地震计以及REFTEK-130s数据采集器。勘选发现,观测场地干扰比较小,观测环境较优,期间共记录到波形清晰且完整的矿震3次、近震6次,原始波形数据经去倾、去均值等预处理后,用于频谱分析。9次事件参数见表 1,其中地震数据来自黑龙江省地震台网正式编目,天然地震和非天然地震已在编目中注明。矿震震源深度较浅,对于ML > 2.0矿震,矿区附近居民有较强震感。在矿震判别中,结合了鹤岗矿区附近的实地调查结果。
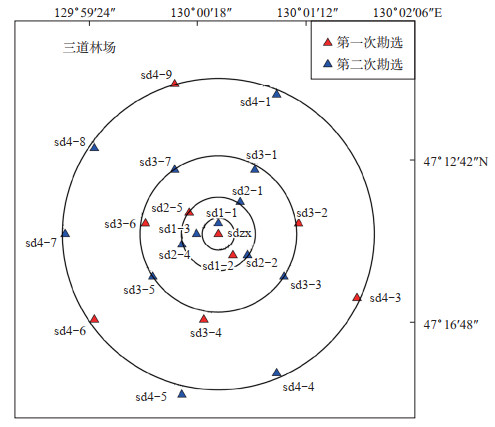
|
图 1 站点分布 Fig.1 Sites distribution |
| 表 1 台阵勘选期间记录的地震 Table 1 Earthquakes recorded during the survey |
王风(2013)、张萍(2005)、靳玉贞等(2015)、杨柳(2015)等诸多研究者对矿震和天然地震频谱特征差异进行了研究,分析结果汇总如下:①矿震一般初动向下,天然地震初动方向不定,由震源机制决定。矿山地震从发震机理上可分为以下2种:一种是与开采面破裂相关,采矿业称为冲击地压,以塌陷为主;另一种与大的间断面(断层)有关,称为矿震,这种矿震的震源机制与天然地震有相似之处,具有双力偶机制(张华等,2014);②矿震频率成分较单一,优势频率集中在1—3 Hz,而天然地震的优势频率较丰富,集中在3—15 Hz;③矿震振幅衰减比天然地震快,天然地震一般持续时间较长;④矿震震源较浅,面波发育,而天然地震面波不发育。对比分析2次勘选过程中所有子台记录的同一矿震和同一天然地震波形,结果见图 2、图 3,其中图 2为矿震波形,图 3为近震波形。在图 2和图 3中选择具有共同特征的典型波形,以sd1-2子台5月16日记录的2.7级矿震和sd3-1子台8月22日记录的3.1级天然地震为例,分析矿震和天然地震频谱的异同,结果见图 4。
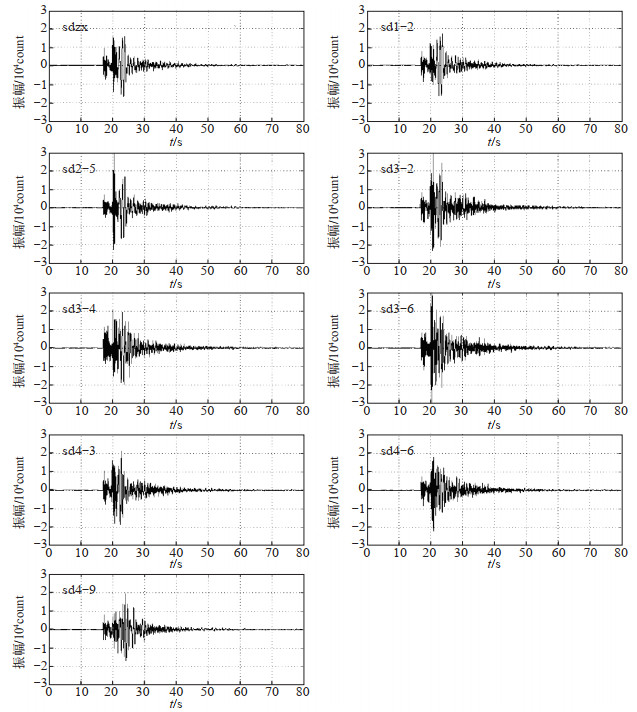
|
图 2 第一次勘选所有子台记录的矿震波形 Fig.2 Mine earthquake waveform recorded by all sites during the first survey |
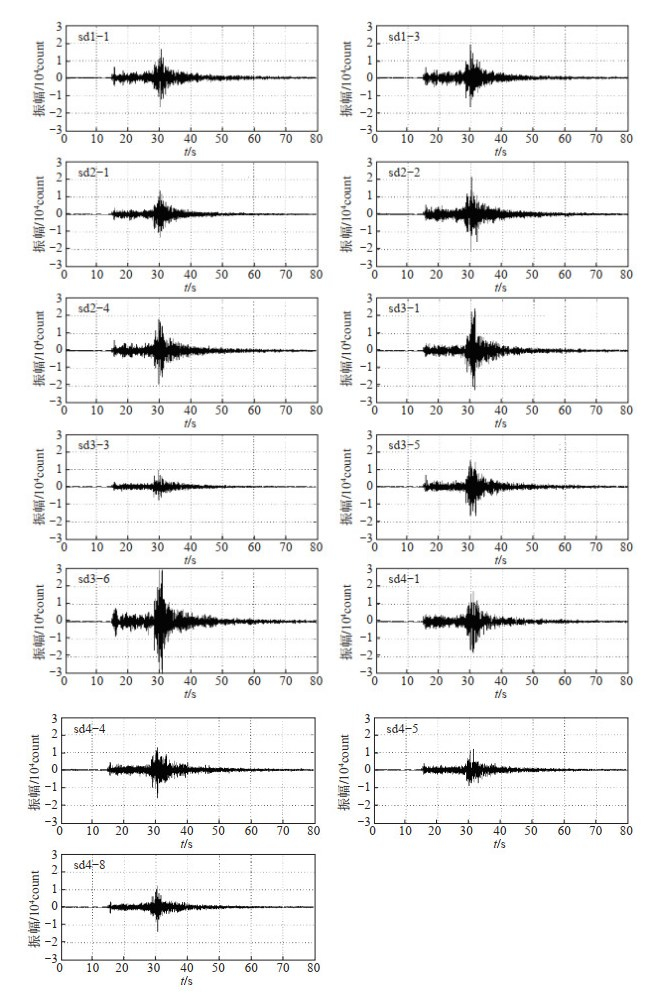
|
图 3 第二次勘选所有子台记录的天然地震波形 Fig.3 Natural earthquake waveform recorded by all sites during the second survey |
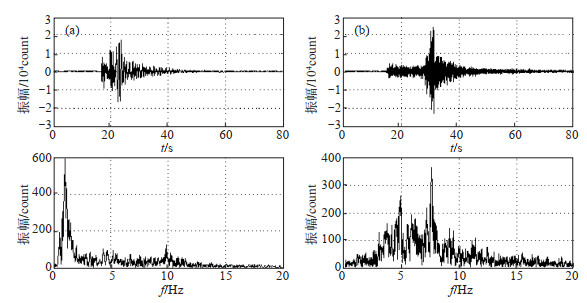
|
图 4 sd1-2记录的矿震波形、振幅谱(a)及sd3-1记录的天然地震波形和振幅谱(b) Fig.4 Mine earthquake waveform and spectrum recorded at sd1-2 station (a) and natural earthquake waveform and spectrum recorded at sd3-1 station (b) |
由图 4可见:①此次2.7级矿震初动方向均向上,与矿塌初动向下特征不一致,分析认为,此次矿山地震可能为非塌陷矿山地震;②矿震优势频率集中在1—3 Hz,天然地震在3—15 Hz,与已有认识一致;③矿震的能量衰减比天然地震快,在波形和频谱中显示并不明显;④矿震面波发育,与已有认识一致。综合分析认为,本次勘选记录的地震频谱特征与已有研究一致,各子台特征也较一致,从子台频谱一致性角度认为,勘选场地适合作为地震台阵建设场地。
3.2 EMD(EEMD)分解利用HHT对地震信号进行EMD分解,得到的IMF分量会受极值点影响,若极值点分布不均则出现模态混叠现象。针对这一不足,Huang等(1998)把白噪声引入待分析信号,提出聚合经验模态分解(EEMD)方法,有效解决了EMD的混频现象(卢俊等,2019)。本文采用EEMD方法进行数据处理。
定义方差为平方的均值减去均值的平方,其大小反映了各个模态所包含信号能量的比重,各模态方差贡献率αk(石瑞敏,2014)为
| ${\alpha _k} = \frac{{\overline {\chi _k^2} - {{\left({\bar \chi _k^2} \right)}^2}}}{{\sum\nolimits_{k = 1}^N {\left({\overline {\chi _k^2} - {{\left({\bar \chi _k^2} \right)}^2}} \right)} }}$ | (2) |
式中,k为第k个模态,N为模态总个数,xk为分解的第k个模态的地震波振幅值。
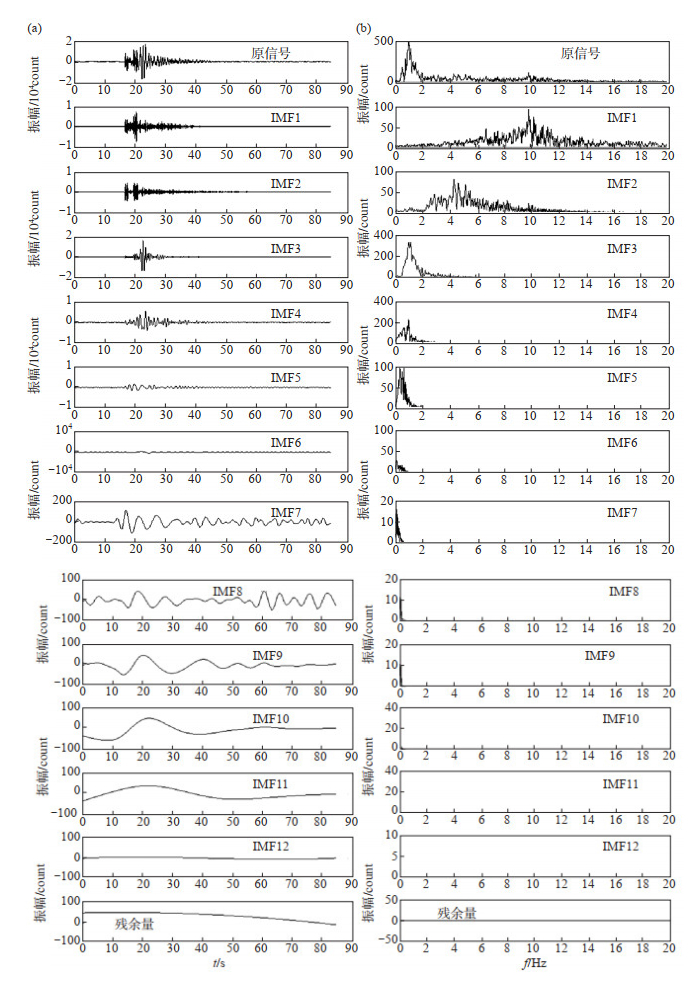
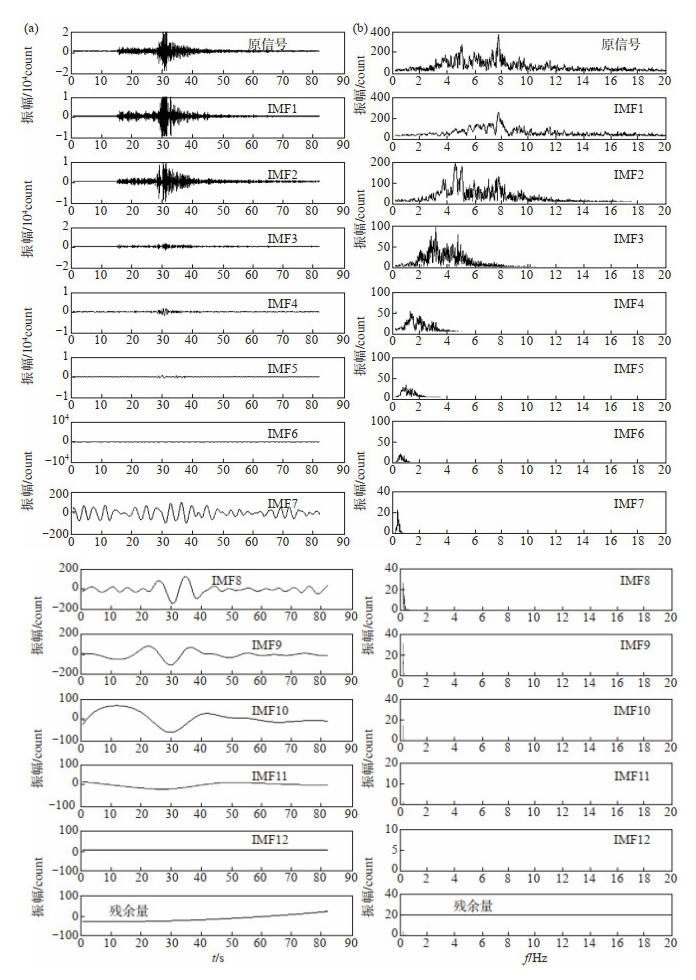
采用EEMD方法,得到不同时间尺度的矿震和天然地震的各IMF分量,结果见图 5、图 6,其中:(a)图给出原始信号及IMF分量:第一个子图为原始信号,依次为IMF1—IMF12,最后一个子图为残余分量RES;(b)图为对应傅里叶谱频率成分。对比矿震和天然地震的各模态分量及频谱特征,可以得出以下认识。
|
图 5 矿震各IMF分量(a)及对应傅里叶频谱(b) Fig.5 IMF components (a) and Fourier spectrum (b) of mine earthquake records |
|
图 6 天然地震各IMF分量(a)及傅里叶频谱(b) Fig.6 IMF components of the natural earthquake (a) and Fourier spectrum (b) |
(1)矿震和天然地震均被分解为13个IMF分量,按时间尺度从大到小依次排列,即先分解高频再分解低频,IMF1频率最高,波长最短。随着分解的进行,所得IMF频率逐渐降低,波形越来越长,至分解最后一个残差余量。
(2)对于矿震,一般在第3个或第4个IFM分量可识别出短周期面波成分,而天然地震的IMF分量无短周期面波成分,此为矿震和天然地震的明显区别。
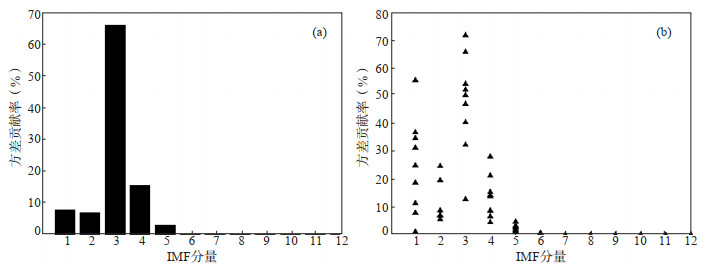
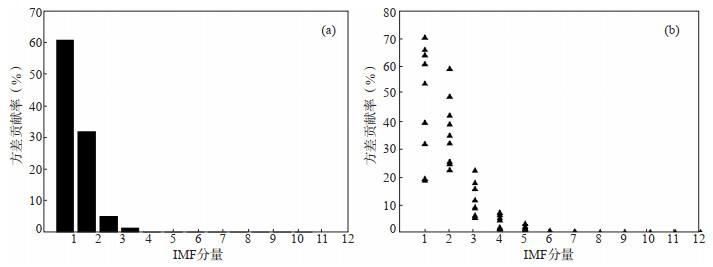
(3)图 7(a)和图 8(a)给出矿震和天然地震各IMF分量的方差贡献率,图 7(b)和图 8(b)给出所有子台的方差贡献率汇总。由图 7、图 8可见,矿震和天然地震能量均主要集中在前几个模态,随着模态的增加,天然地震方差贡献率单调减小,而矿震在第3个模态前后因出现短周期面波,方差贡献率出现极大值,振幅最大,面波包含了信号的大部分能量。
|
图 7 矿震各IMF(a)及所有子台方差贡献率汇总(b) Fig.7 The contribution rate of each IMF variance of mine earthquake records (a) and summary of all sites (b) |
|
图 8 天然地震各IMF(a)及所有子台方差贡献率汇总(b) Fig.8 The contribution rate of each IMF variance of nature earthquake (a) and a summary of all sites (b) |
(4)从分解出的各模态频谱中明显可见,在频率1 Hz以上,矿震频谱成分较单一,仅2个固有模态成分(固有振动成分),而天然地震成分更复杂,有3—4个固有模态成分。
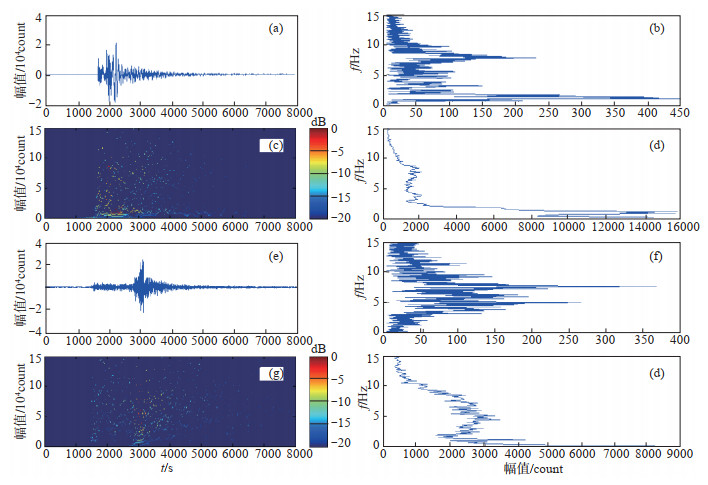
3.3 时频特征图 9给出矿震和天然地震的时频分析结果,其中(a)、(b)、(c)、(d)分别为矿震波形及FFT谱、HHT谱和边际谱;(e)、(f)、(g)、(h)为天然地震波形及FFT谱、HHT谱和边际谱。
|
图 9 矿震和天然地震波形的HHT时频分析 (a)矿震波形;(b)矿震波形FFT谱;(c)矿震波形HHT谱;(d)矿震波形边际谱;(e)天然波形形;(f)天然地震形FFT谱;(g)天然地震波形HHT谱;(h)天然地震波形边际谱 Fig.9 HHT time-frequency analysis for seismic records of mine earthquakes and natural earthquakes |
对比矿震和天然地震的原始波形及HHT时频谱,明显可见,在时间上,波形和时频谱具有较好的对应关系,而HHT时频谱可细致刻画地震波在某时刻的频率信息。
矿震和天然地震HHT时频谱的不同特征表现在:①低频部分:矿震频率具有低频集中的特点,连续且持续时间较长。天然地震时频谱呈现低频信号时间不连续,Pg震相一出现低频信号即快速消失,在Pg低频信号消失一段时间后,Sg震相重现低频信号;②高频部分:矿震高频部分与低频信号同步出现,并伴随在整个地震动时段,强度低于低频信号。从边际谱(h)图可以看出,天然地震在频率5 Hz上下信号最强,持续时间最长。对比(e)图和(g)图,且5 Hz频率信号从地震信号开始至结束贯穿整个地震时段。
对比矿震和天然地震的傅里叶谱及边际谱,发现二者形态较一致,边际谱反映了HHT谱中各频率值在时间轴上的累加,频率信息更真实。
对比矿震和天然地震的HHT时频谱及边际谱,可见:矿震在1—2 Hz低频部分频率累加值最大,对应边际谱能量相对最强;天然地震在3—10 Hz频段频率累加值最大,对应边际谱中能量相对最强。在天然地震和矿震波形的传播时段中,天然地震衰减时间较长。
总之,在HHT时频谱图像上,矿震和天然地震存在明显不同,二者容易被区分出来。
4 结论与讨论通过对鹤岗地震台阵勘选期间记录的矿震和天然地震进行频谱和时频特征进行分析,得到以下结论。
(1)地震台阵各子台波形和频谱特征一致性较好,与现有研究结果较一致,表明勘选场地各子台观测环境至少相差不大。各子台波形和频谱特征较一致可作为勘选场地适宜建设地震台阵的依据之一,说明三道林场适合作为地震台阵的建设场地。
(2)EEMD分解的第3和第4模态可以将矿震面波成分作为独立分量分解出来,可作为识别矿震和天然地震的依据。在此基础上,可深入开展以下工作:如何更准确地提取矿震面波,并进行计算机自动提取和识别;利用EEMD分解得到频率成分不同的各模态分量,去除不需要的频段信息,重构原始信号波形,去除噪声以提高信噪比。
(3)矿震和天然地震波形的时频特征存在明显差别。从频率演化过程来看,矿震频率值始终集中在低频段,边际谱中低频段累加能量值最高。而天然地震频率值在时频图上相对分散,在频率5 Hz上下持续时间较长,衰减较慢,这是由震源性质决定的。无论是开采面破裂还是间断面破裂,矿震的震源深度均较浅,面波发育,低频段能量较高。而天然地震的震源机制相对复杂,若干微小破裂组成震源,每个微小破裂的发生均有一定过程,且其震源较深,地震波多在致密坚硬的岩层中传播,能量和高频成分损耗少,使得记录的波动持续时间较长。
文中部分图件采用GMT绘制,数据采集由参与野外勘选的同事负责,勘选数据由黑龙江“一带一路”项目提供,且审稿专家对论文撰写提出宝贵的意见和建议,在此表示诚挚的感谢。
戴勇, 高立新, 张帆, 等. 数字地震波时频分析[J]. 地震地磁观测与研究, 2017, 38(6): 10-16. |
和雪松, 李世愚, 沈萍, 等. 用小波包识别地震和矿震[J]. 中国地震, 2006, 22(4): 425-434. DOI:10.3969/j.issn.1001-4683.2006.04.010 |
黄光南.希尔伯特黄变换及其在地震资料分析处理中的应用[D].青岛: 中国海洋大学, 2009.
|
靳玉贞, 林木金, 范晓瑜, 等. 山西地区爆破、塌陷(矿震)特殊地震动特征识别[J]. 地震地磁观测与研究, 2015, 36(3): 63-66. |
梁宏, 朱永莉, 李大虎, 等. 基于希尔伯特-黄变换的九寨沟M 7.0地震加速度记录时频分析[J]. 国际地震动态, 2019, 11061106(7): 9-16. |
刘莎, 杨建思, 田宝峰, 等. 首都圈地区爆破、矿塌和天然地震的识别研究[J]. 地震学报, 2012, 34(2): 202-214. DOI:10.3969/j.issn.0253-3782.2012.02.007 |
卢俊, 吴建星. 基于EEMD方法的地下矿山微震信号去噪研究[J]. 有色金属(矿山部分), 2019, 71(4): 12-18. |
石瑞敏, 杨兆建. 基于改进EMD的多绳摩擦提升机载荷信息特征提取[J]. 煤炭学报, 2014, 39(4): 782-788. |
万永革. 数字信号处理的MATLAB实现[M]. 北京: 科学出版社, 2012: 384-406.
|
王风, 吕震, 刘兵, 等. 邹城地区矿震、爆破和(天然)地震事件的特征分析[J]. 地震地磁观测与研究, 2013, 34(1/2): 82-86. |
武安绪, 吴培稚, 兰从欣, 等. Hilbert-Huang变换与地震信号的时频分析[J]. 中国地震, 2005, 21(2): 207-215. |
杨柳, 张可佳, 杨桐, 等. 长春地震台网地震、爆破与矿震记录的识别[J]. 高原地震, 2015, 27(2): 1-5. |
杨培杰, 印兴耀, 张广智. 希尔伯特-黄变换地震信号时频分析与属性提取[J]. 地球物理学进展, 2007, 22(5): 1585-1590. |
张华, 姚宏, 陈鑫, 等. 矿震识别及成因研究进展[J]. 国际地震动态, 2014, 11061106(3): 4-12. |
张萍, 蒋秀琴, 苗春兰, 等. 爆破、矿震与地震的波谱差异[J]. 地震地磁观测与研究, 2005, 26(3): 24-34. |
张义平, 李夕兵. Hilbert-Huang变换在爆破震动信号分析中的应用[J]. 中南大学学报(自然科学版), 2005, 36(5): 882-887. |
郑建常, 徐长朋, 赵金花, 等. 基于S变换的矿山地区地震波形时频分析[J]. 地震地磁观测与研究, 2014, 35(5/6): 8-14. |
钟佑明, 秦树人, 汤宝平. 希尔伯特-黄变换中边际谱的研究[J]. 系统工程与电子技术, 2004, 26(9): 1323-1326. |
Huang N E, Shen Z, Long S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proc R Soc A, 1998, 454(1 971): 903-995. |
 2020, Vol. 41
2020, Vol. 41

