野外布设的大量地震台站不仅可以记录到地震信号，也记录到大量连续噪声信号。这些噪声信号来源包括地球震动、大气气压变化、固体潮汐、海浪拍击海岸、生活噪声等。连续的背景噪声记录曾被视为无用的干扰信号，在研究天然地震信号时，以各种方法予以剔除。后来，科学家发现背景噪声记录也能用于地下速度结构的研究（Claerbout，1968；Duvall et al，1993；Lobkis et al，2001），而且具有较高的分辨率。

理论研究表明，通过背景噪声互相关及时间域叠加，可以提取台站间的格林函数，基于经验格林函数得到面波频散曲线，可用地震层析成像方法对面波速度进行反演，得到地球内部的速度结构（顾勤平等，2020）。但背景噪声源分布的均匀性对互相关函数和经验格林函数的近似程度比较重要（Roux et al，2005）。由于地球内部结构的不均匀性，实际观测到的噪声分布并不均匀，有必要分析研究区域的背景噪声源在时空上的特征，进而提高反演结果的准确性。文中基于祁连山地区78个地震台站的垂直分量连续波形记录，分析该地区背景地噪声特征。

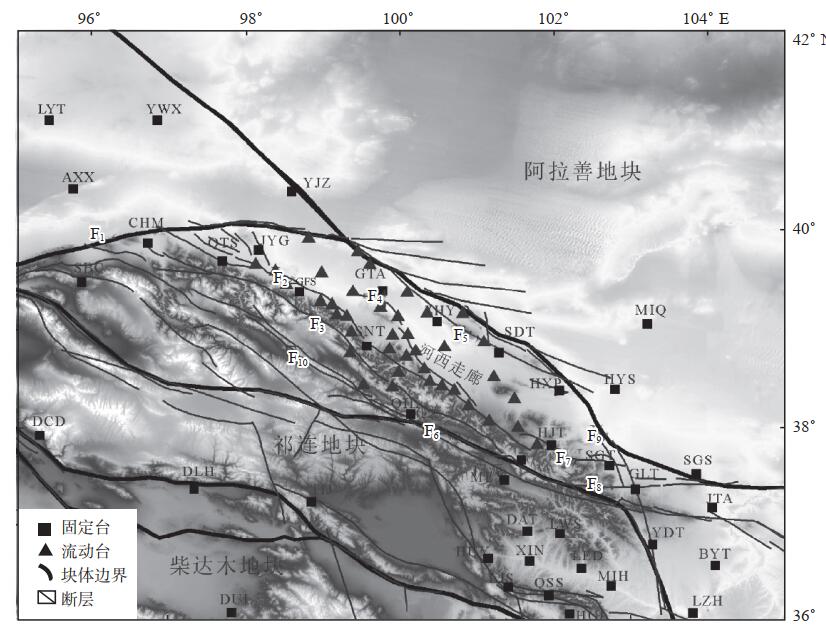
祁连山地区位于青藏高原东北缘，地处青藏地块与阿拉善地块的挤压缝合带，构造活动强烈、地震活动频繁。研究该区域背景噪声源的时空特征，对于认识青藏高原地壳速度结构具有重要的科学意义。收集整理甘肃主动源重复探测项目沿祁连山北缘断裂带走向布设的40个流动台和周边所属甘肃省、青海省的38个固定台（图 1）的连续背景噪声记录，其中流动台配备短周期数字地震仪，频带响应为2 s—100 Hz；固定台配备宽频带数字地震仪，频带响应为60 s—50 Hz。

图 1(Fig.1)

图 1 祁连山地区台站分布和构造背景 F1 阿尔金断裂; F2 祁连山北缘断裂; F3 昌马—俄博断裂; F4 榆木山断裂; F5 龙首山南缘断裂; F6 托莱山断裂; F7 皇城-双塔断裂; F8 冷龙岭断裂; F9 武威—天祝断裂; F10 阴凹曹断裂 Fig.1 Distribution of seismic station and tectonic setting in Qilian Mountains

选取78个地震台站2014年8月—2015年12月的垂直分量连续波形记录，计算台站间的互相关函数，采用归一化振幅方法，研究该地区在5—10 s和10—20 s两个周期内背景噪声源能量的时空变化特征，其中海洋噪声源分布对台阵的影响见图 2。

图 2(Fig.2)

图 2 海洋噪声源分布对台阵的影响 Fig.2 Distribution of ocean noise source influence on station array

任意2个台站间计算的互相关函数，其振幅取决于2个台站连线方向的能量流（Paul et al，2005）。如果台站两侧的噪声源均匀分布，说明2个方向的能量流是相同的，则互相关函数的振幅和到时大小是完全相同的；如果台站两侧的噪声源分布不均匀，则会发现互相关函数的到时相同、振幅不对称，说明互相关函数正负分支能量流的来源方位不同。同时，互相关函数2个方向的能量流在分布时间上表现为一定的季节性变化，会影响频散曲线的稳定性（徐果明等，2000）。因此，有必要分析背景噪声源的分布特征和季节性变化特征。Stehly等（2006）选取美国东部、欧洲西部、加利福尼亚的地震台网垂直分量背景噪声记录，通过分析互相关函数因果信号和非因果信号的不对称性，发现不同频带的噪声起源是不同的：环境背景噪声在5—10 s和10—20 s之间存在2个明显的峰值，10—20 s之间存在的峰值称为第一类地脉动，该频段噪声随着季节的变化而变化，是由深部海水的波浪引起的，冬季来源于北大西洋和北太平洋，夏季来源于印度洋和南太平洋；5—10 s之间存在的峰值称为第二类地脉动，该频段噪声不随季节变化，是由海浪和海岸线的相互作用产生的。但Kedar等（2007）指出，海浪和海岸线非线性的相互作用并不是第二类地脉动的唯一来源，在特定的深海海域也会产生相同频段的噪声。

在方位角计算中，所用定义与地震事件中方位角计算原理相同，则假设其中一个台站为地震发生事件，另一个台站为地震接收台站。通过计算两台站间的互相关函数，得到2 181条路径上的频散曲线，对这些满足信噪比SNR≥5、Δ≥3λ（Δ为台间距，λ为波长）的互相关函数的噪声特征进行分析，研究其背景噪声能量流在不同频段、不同方位、不同季节的主要来源方向。

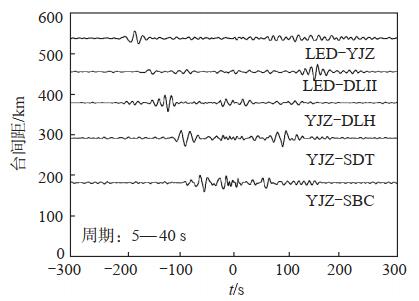
归一化振幅可以表征背景噪声能量强度，值越大则噪声能量流越强。其计算原理为：计算台站对间的互相关函数，分析其正负分支面波到时窗内的最大振幅和方位角分布，用最大振幅乘以台站间距的平方根，将振幅归一化，得到取值范围在0—1的归一化振幅值，则所得振幅分布均与方位角有关。数值大的方位，代表了背景噪声来源的主要方位。图 3给出一些具有代表性的互相关函数和振幅值，其中正的分支分别表示从LED、LYT等向YJZ、SBC传播的波，负的分支表示沿相反方向传播的波。LED—YJZ和LED—DLH不对称，表明噪声在正负方向上的分布不均匀；YJZ—SDT比较对称，表明噪声在正负方向上近似均匀分布。

图 3(Fig.3)

图 3 代表性互相关函数 Fig.3 Some representative cross-correlation functions

选取祁连山地区78个地震台站2014年8月—2015年12月的垂直分量连续波形记录，采用Bensen等（2007）给出的噪声层析成像数据预处理方法进行数据处理。具体处理流程为：原始格式数据转换为sac格式文件，截取一天的数据存储为一个文件，然后进行重采样（采样率为10 Hz）、仪器响应校正、去均值和去倾斜、带通滤波处理，再进行时域归一化以消除地震事件、仪器畸变等非静态干扰，频域归一化（频谱白化）来拓宽背景噪声频带宽度和消除单频信号的干扰，最后进行互相关函数的计算和叠加。

在以上数据预处理基础上，将单台预处理数据进行互相关计算，并叠加获得最终互相关函数。任意一个互相关函数包括一个正的分支和一个负的分支，正的分支称为因果信号，负的分支称为非因果信号，2个分支分别代表波动传播的2个方向。

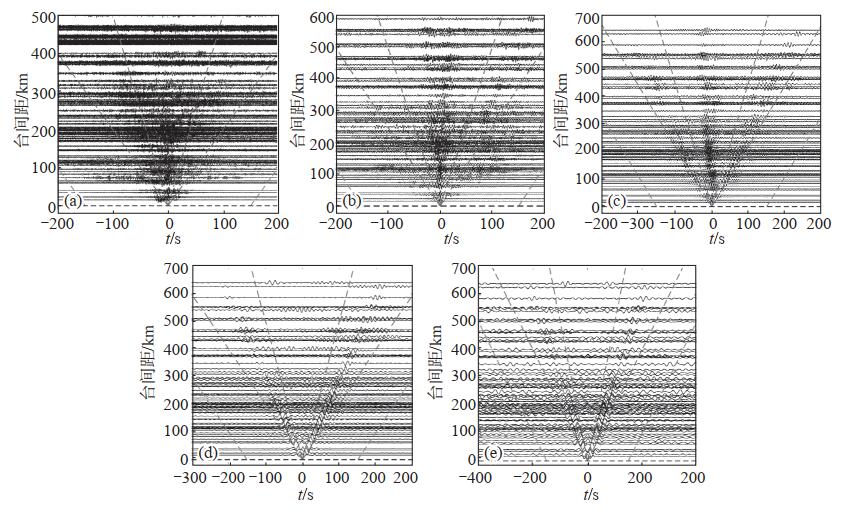
前人研究（Lobkis et al，2001；Weaver et al，2004）表明，如果噪声源在空间上均匀分布，互相关函数的正向和逆向结果应该是对称的。但实际上，互相关函数的正负分支并不对称，从而影响反演结果的可靠性。为此，Lin等（2008）建议，将互相关函数的正负分支反序后叠加，形成对称分量，而对称分量的信噪比在各个周期上均有所提高。以ZDY01台站作为噪声源，采样率为10 Hz，计算与其余77个台站在不同滤波范围内的互相关函数波形，则互相关函数示意图见图 4。

图 4(Fig.4)

图 4 ZDY01与其余77个台站不同滤波范围的互相关函数波形示意(采样率为10 Hz) (a)周期为0.5—2 s; (b)周期为2—5 s; (c)周期为5—10 s; (d)周期为10—20 s; (e)周期为20—40 s虚线标出信号窗口(面波到时窗内的波形数据)和噪声窗口(信号窗口后150 s范围的波形数据) Fig.4 Cross-correlation function of ZDY 01 with other 77 stations (sampling rate is 10 Hz)

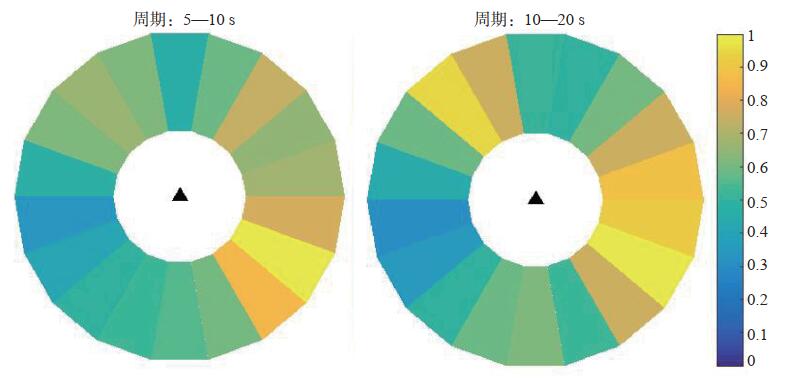
利用研究区域2014年8月—2015年12月共17个月的噪声互相关函数进行叠加计算，得到所有台站对的互相关函数，分析计算每个台站对5—10 s和10—20 s周期范围内的噪声能量来源优势方位。图 5给出所有台站对在2个微震带互相关函数与方位有关的振幅分布，该方位角与归一化振幅密切相关，不同方位上振幅较大者表示沿该方向传播的噪声能量较强。设正北方向为0°，顺时针转到360°，将背景噪声能量优势分布方位角分成18份，每份20°。由图 5可见，第二微震带（5—10 s）的噪声能量来源优势方位角为100°—160°，在310°—350°方位也有相对微弱的能量分布，即噪声源的位置主要指向东南部的太平洋；而第一微震带（10—20 s）噪声能量来源优势方位角主要集中在70°—160°、300°—350°，噪声源的位置主要指向东南部的太平洋和西南部的北大西洋。

图 5(Fig.5)

图 5 所有台站对不同周期噪声互相关函数不同方位上归一化振幅分布 Fig.5 The normalized amplitude distribution of all station-pairs for different periods of noise cross-correlation functions in different directions

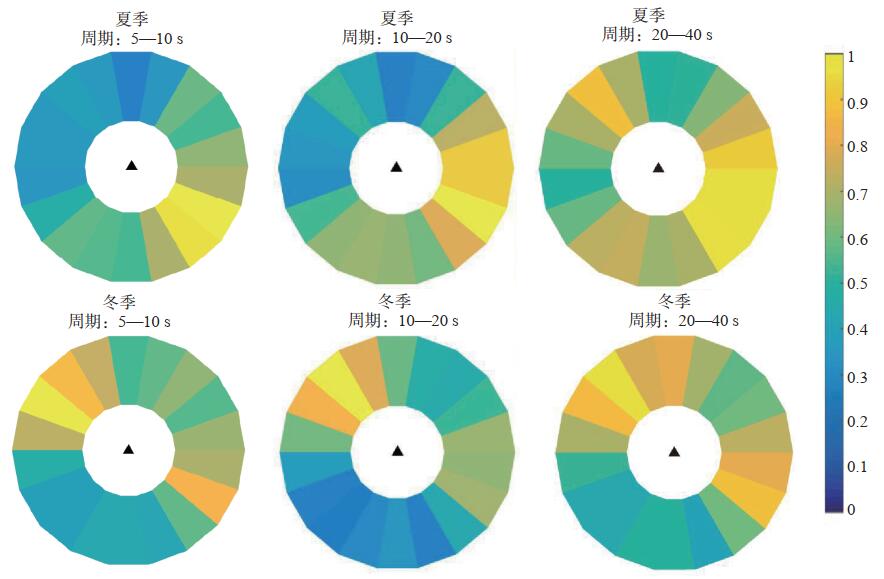
将2015年12个月的所有台站对互相关数据按季节叠加，得到祁连山地区冬季（2015年1月—2月、11月—12月）和夏季（2015年6月—9月）的背景噪声互相关函数，绘制所有台站对在5—10 s、10—20 s、20—40 s频带内随季节的归一化振幅方位角分布图，结果见图 6，据此分析研究区域不同频带的噪声源能量在不同方位随季节变化的规律。由图 6可见，不同频带的噪声能量优势方位表现出明显的季节变化特征。5—10 s周期背景噪声的能量优势来源在夏季集中在110°—170°方位，冬季则集中在300°—350°方位，但在110°—150°方位也有相对微弱的能量分布，可见第二微震带（5—10 s）的背景噪声能量在夏季主要来源于太平洋的海洋活动，冬季主要来源于大西洋的海洋活动。10—20 s周期背景噪声的能量优势来源在夏季集中在70°—150°和170°—230°方位，在冬季则集中在290°—350°和70°—130°方位，则第一微震带噪声能量在夏季主要来源于印度洋的海洋区域，冬季主要来源于北大西洋和太平洋。因此，5—20 s周期段的背景噪声源在时间上表现出明显的季节变化特征。20—40 s周期段的瑞利面波互相关函数随季节的变化较小，可认为该周期段与5—20 s周期段的噪声起源是不同的，也可认为噪声源近似均匀分布。前人研究认为，长周期噪声是由大气、海洋和海底的相互作用在海岸附近形成的（Rhie et al，2004）。

图 6(Fig.6)

图 6 夏季和冬季不同频段的噪声强度方位分布 Fig.6 Azimuthal distribution of noise intensity in different frequency bands in winter and summer

第二微震带（5—10 s）的噪声能量来源优势方位角为100°—160°，在310°—350°方位也有相对微弱的能量分布，即噪声源的位置主要指向东南部的太平洋。而第一微震带（10—20 s）噪声能量来源优势方位角主要集中在70°—160°、300°—350°方位，噪声源的位置主要指向东南部的太平洋和西南部的北大西洋。把2015年12个月的所有台站对互相关数据按季节叠加，得到祁连山地区冬季和夏季的背景噪声互相关函数，5—10 s、10—20 s两个不同频带的噪声能量优势方位均表现出明显的季节变化特征。

台站方位角分布的均匀性对统计结果具有一定影响，但从上述方法得到的结果来看，祁连山地区背景噪声源在2个微震带的时空变化与王伟涛等（2011）、马小军等（2014）在不同地区得到的结果类似，说明文中台站方位角的分布对成像结果影响不大。此外，在噪声面波成像时可通过长时间叠加来等效均匀噪声源，以消除噪声源方位和季节变化对成像结果可能产生的误差。

甘肃省地震局提供连续波形数据，中国科学技术大学姚华建教授提供背景噪声计算程序，在此表示感谢。