随着城市轨道交通系统的蓬勃发展,轨道交通引起的地面环境振动不仅对沿线医院、古建筑、居民区等敏感建筑的结构安全以及其中居民的日常工作生活产生很大的影响,对精密仪器等高技术设备的正常工作以及高技术产业的生存也带来灾难性的影响(雷军等,2010).轨道交通引起的振动越来越受到广泛的关注,交通振动所引起的振动公害已被列为世界七大环境公害之一.利用地球物理的方法解决环境问题(中国地球物理学会环境地球物理专业委员会,1997),将为振动问题提供更全面的认识与解决思路,为城市规划和地铁线路设计等提供参考.
地面振动可看作是振源与地层耦合作用的结果,经过对地铁周边地面环境振动的大量实际观测数据分析显示不同地面交通与地铁源频率对地表环境振动产生不同的影响(栗润德等,2007).因此了解不同频率对地表振动的影响以及振动随距离的衰减成为一个非常重要的课题.
地铁诱发环境振动问题的研究主要是通过环境振动实测和数值模拟两种途径,目前国内外对地铁列车引起的地面环境振动进行了大量的研究(Chatterjee et al., 2003;Degrande et al., 2006;Karlström and Boström,2006;Gupta et al., 2009).Wolf(2003)研究了地铁运行产生的6.3 Hz以下的低频振动对华盛顿大学天文楼及生命科学楼的影响,通过利用两台CMG40T地震仪观测地球物理楼下的环境振动, 并利用测量的地面振动数据和和岩土数据建立隧道数学模型进行有限差分分析.北京大学环境振动监测与评估实验室(雷军等,2013)通过对地铁站及地铁沿线附近地面进行长期观测,并采用有限元方法预测地铁运行产生的振动, 来评估地铁运行对北京大学精密实验仪器的影响(耿万里等,2014).栗润德等(2007)通过采用Lance AS130型高灵敏度加速度传感器进行地面振动数据的采集和记录, 来测试与分析北京地铁1号线的地面振动响应, 得出了环境背景振动、公交车等地面车辆以及地铁的地面振动响应规律.北京市地铁总公司、北京市环境保护局、北方交通大学等(王毅,1992;夏禾等,1999;陶连金等,2003;谢伟平和孙洪刚,2003;楼梦麟等,2009;孟宪春等,2010;丁德云等,2011)也通过理论分析、数值模拟和现场试验的方法研究铁路、地铁、高架轻轨列车作用下的地面、隧道及高架桥梁的振动及其对周围环境和建筑物影响的研究成果.台湾大学的杨永斌① (Yang and Hung, 2001, 2009; Yang et al., 2008)、Fujikake(1986)采用数值分析的方法对高速铁路的环境振动影响进行了系统的研究和预测,并提出了降低环境振动影响的措施.雷军等(2010)在北京地铁4号线沿线北京大学东门附近进行环境振动监测,结果显示该地区早上6:00至晚上23:00多个时段的环境振动垂直分量在1~20 Hz内的多个频率点超过北大部分实验室正常工作的环境振动限制,而原因在于地层中隧道空腔的形成使地层固有振动在某些频段被放大,从而使地面交通和其他环境因素引起的环境振动幅值提高.
① 杨永斌. 1996.高速列车所引致之土壤振动分析[R].台湾:台湾大学.
由于振动观测受周围环境振动影响较大,实际观测到的数据都是地面交通与地铁共同作用的结果,很难对二者进行分离来量化地面交通与地铁对地面振动的影响(郑鑫等,2013),为了从理论上解释不同频率地面以及地下源对地面环境振动的影响,本文通过有限元数值模拟方法来研究1~20Hz频率源分别作用于地面和地下以及地面与地下同时作用时地表的环境振动响应, 通过与地面实际观测资料对比,来进一步验证观测所得到的结论,通过本文的研究希望对地铁沿线高精密仪器实验室隔振、古建筑隔振、地铁减振以及地铁选线等工程提供参考.
1 方法在进行地铁振动数值模拟时,载荷的输入包括输入力和加速度记录两种方式.力的方式包括简单力(脉冲力或谐波型力等)和通过对记录加速度做数定分析得到的地铁轮轨作用的数定力,由于本研究不考虑实际地铁振动引起地面振动位移振幅的精确解,即不关注源量级的大小,仅考虑地面与地下不同频率源对地面振动的影响,所以采用简谐加速度载荷作为输入源(耿万里等, 2013, 2014;张琼等,2013).
本研究选择采用FEPG有限元软件进行二维有限元数值计算(梁国平,2009;白冰和李小春,2011), 并对生成有限元程序做改进, 使得振动源按照上述加速度记录方式输入.
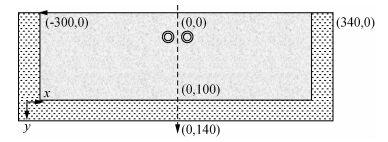
2 有限元模拟 2.1 几何模型本文有限元数值计算采用的二维几何模型见图 1,模型尺寸为600 m×100 m,隧洞中心埋深20 m,隧洞外径3 m,内径2.7 m.为了防止边界反射效应影响计算结果,经过测试将阻尼层厚度设置为40 m可以吸收掉绝大部分的反射波.在地表黑色箭头所示方向以十米为间距布置测点,测线从地面零点开始(零点位于两隧道中间),共29个测点.记录该测点在不同时刻的加速度值,最后对每个测点的时域加速度记录取有效值得到地面振动随距离的变化曲线,有效值按照式(1)计算,其中ae为振动加速度有效值,N记录数据点数,a为记录的加速度值.二维模型地层参数见表 1.公式(1)为
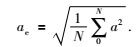
|
(1) |
|
图 1 二维几何模型 Figure 1 Geometry of the 2D model |
|
|
表 1 有限元模型地层参数表 Table 1 Strata parameters of finite element model |
为了研究不同频率地面以及地下源对地面环境振动的影响,以下分3种工况进行计算.具体工况介绍见表 2.
|
|
表 2 3类工况介绍 Table 2 Three kinds of working condition |
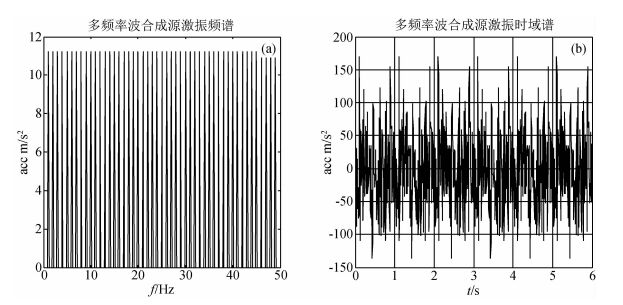
表 2中第三种工况地下载荷的时域与频域波形图见图 2,工况3地下载荷采用1~50 Hz等幅源,即地下载荷频段在1~50 Hz,50个单频波叠加合成的波形,且每个频率波的振幅大小一致.图 2a为等幅源的频谱,从图中看出第三种工况的地下载荷包含的频段为1~50 Hz,且每个频率的幅值相同,图 2b为时域波形图,即实际的地下载荷加载波形.需要申明,本文计算采用的输入载荷做了简化,不论是设置每个频段幅值相等的等幅源还是简谐源,都是为了更好的分析比较不同频率振动在传播到地表的过程中的衰减情况,频段的选择也是考虑到实际振动监测发现的对地表振动影响比较显著的频段.
|
图 2 1~50 Hz等幅源的时域与频域波形 Figure 2 1~50Hz waveform in time domain and frequency domain |
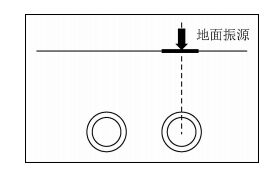
地面加载模型示意图见图 3,黑色箭头为地面加载点位置,底部同心圆代表隧道空腔,通过对二维有限元模型的地面加载点分别采用1~20 Hz单频正弦谐波激振,分析不同频率地面输入载荷的地面振动响应.经计算得到地下源激振工况的地表振动加速度,见图 4.
|
图 3 地面加载模型 Figure 3 A schematic diagram of the source on the ground |
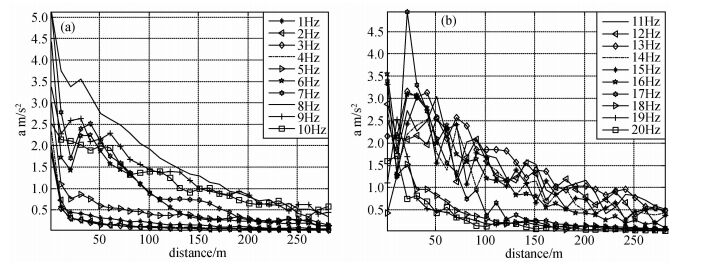
|
图 4 1~20 Hz频率地面加载的地表振动加速度响应 Figure 4 1~20Hz ground vibration of the source on the ground |
图 4显示,在地面激振的情况下,1~5 Hz源的地面振动在20 m处以后衰减很慢,当源频率大于5 Hz以后随着频率增加地面振动随距离衰减;当源为8 Hz时地面振动最大,频率大于或小于8 Hz地面的振动均减小,该频段可能是地层自振频率或者地面振动与隧道空腔耦合,使得地面振动在该频段被放大;地面振动在9~17 Hz的地面振动比低频大,大于17 Hz以后地表振动下降;8~15 Hz频段距离地铁250 m范围内能明显看到衰减;16~20 Hz频段内,在距离100 m后地面衰减小,地表 100 m范围内地面振动加速度大.
2.3.2 地下激振地下加载模型示意图见图 5,黑色箭头为地下加载点位置,底部同心圆代表隧道空腔,通过对二维有限元模型的地下加载点分别采用1~20 Hz单频正弦谐波激振,分析不同频率地下输入载荷的地面振动响应.经计算得到地下源激振工况的地表振动加速度,见图 6.
|
图 5 地下加载模型 Figure 5 A schematic diagram of the source underground |
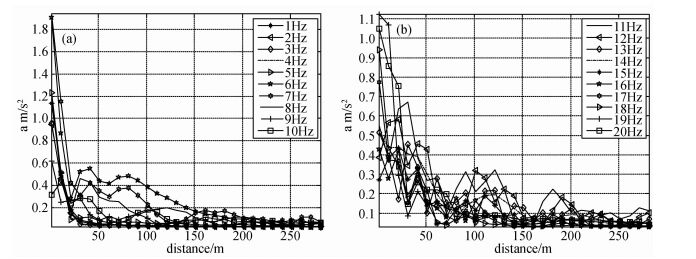
|
图 6 1~20 Hz频率地下加载的地表振动加速度响应 Figure 6 1~20 Hz ground vibration of the source underground |
图 6显示,在地下激振的情况下,1~5 Hz源的地面振动在20 m处以后衰减很慢,当源频率大于5 Hz以后随着频率增加地面振动随距离衰减;当源为6 Hz时地面振动达到最大,频率大于或小于6 Hz地面的振动均减小,该频段可能是地层自振频率或者地面振动与隧道空腔耦合,使得地面振动在该频段被放大;8~15 Hz频段距离地铁250 m范围内能看到波动衰减;16~20 Hz频段内,在距离70 m后地面衰减小,主要是70 m范围内地面振动加速度大.
图 6与图 4比较,认为相同量级地下加载与地面加载产生的地面振动,采用地下加载激发的波穿过隧道衬砌在地层中传播,地层阻尼大,波在到达地面后有很大部分衰减,导致地面加载对地面加载点附近的振动影响显著,但是由于地铁载荷重、速度快,地铁产生的振动量比地面交通大,并且考虑到实际情况下地铁激发的频率丰富,实测地铁振动的地面响应频率主要为10~30 Hz和50~80 Hz,地面交通的地面响应频率主要为10~30 Hz,由于本文是在实测北京地铁4号线沿线北京大学东门附近环境振动监测的振动垂直分量在1~20 Hz内的多个频率点超过北大部分实验室正常工作环境振动限制的背景下探讨不同频率的振动响应,因此只对1~20 Hz频率成分作了研究,所以不能说明地表激振比地下激振对地面振动的影响大,具体影响有待于进一步研究.
2.3.3 地面与地下同时激振地面与地下同时加载的模型示意图见图 7,黑色箭头分别为地面和地下加载点位置,底部同心圆代表隧道空腔,地下加载采用1~50 Hz等幅源,地面加载采用1~20 Hz单频正弦谐波源,分析在地下加载同时存在的情况下,地面不同频率载荷的地面振动的响应.经计算得到地下源激振的地表振动加速度,见图 8.
|
图 7 地下与地面同时加载模型 Figure 7 A schematic diagram of the source both on the ground and underground |
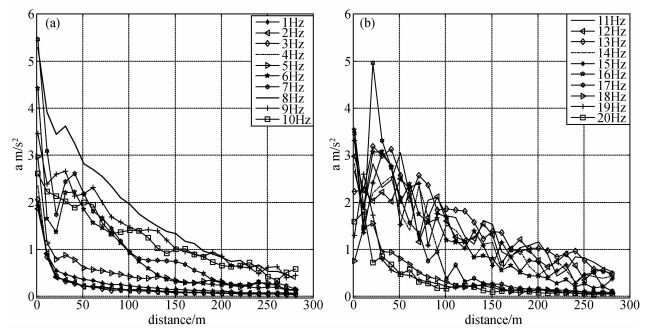
|
图 8 1~20 Hz频率地面与地下同时加载的地表振动加速度响应 Figure 8 1~20 Hz ground vibration of the load both on the ground and underground |
图 8显示:当地面与地下同时激振的情况下,1~5 Hz源的地面振动在20 m处以后衰减很慢,当源频率大于5 Hz以后随着频率增加地面振动随距离衰减;当源为8 Hz时地面振动最大,频率大于或小于8 Hz地面的振动均减小,可能是地层自振频率或者地面振动与隧道空腔耦合,使得地面振动在该频段被放大;8~15 Hz频段距离地铁250 m范围内能看到波动衰减;16~20 Hz频段内,在距离70 m后地面衰减小,主要是地铁70 m范围地面振动影响大.地下采用1~50 Hz等幅源,地面分别采用1~20 Hz简谐源激励产生的地面振动与图 4、图 6比较,结果显示与地面激振模型产生的地面振动在波形上一致,但是在1~5 Hz时近距离处加速度幅值有所增加,因为本文所用的阻尼过大,使得地下源作用时,高频成分在从源到地表的传播过程中衰减,从而地表占主导,但是低频成分衰减慢,导致低频部分增大.
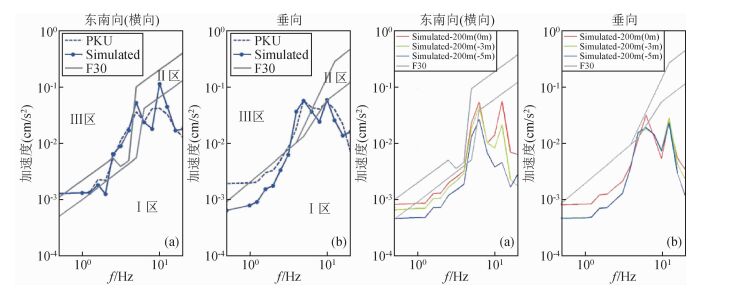
|
图 9 地表振动加速度谱 (a)地铁4号线地表场地点140 m处的模拟加速度三分之一倍频程谱; (b)地铁16号线200 m处实验楼场点的预测加速度三分之一倍频程谱. Figure 9 One-third-octave spectrum on observation site (a)Simulated accelerations in one-third-octave spectrum at the observation site of 140 m from of Subway Line 4; (b) Simulated accelerations at the observation site of 200 m of Subway line 16. |
结合北京地铁16号线对北京大学精密仪器实验楼振动影响预测分析报告和北京地铁16号线对北京大学精密仪器实验楼振动影响综合研究科研试验项目报告①②(耿万里,2014),北京大学环境振动监测与评估实验室(用PKU表示)在场点140 m实测的横向和垂向振动加速度的三分之一倍频程谱曲线在5~6 Hz和8~10 Hz出现峰值, 通过地铁四号线模型校正得到的地铁16号线模型预测的横向和垂向振动加速度的三分之一倍频程谱曲线在6~7 Hz和~10 Hz出现峰值,这些结果都表现出特定的地层结构对某些频段波会有放大效果,使环境振动幅值提高,与本文研究结果具有一致性.
① 北京大学环境振动监测与评估实验室. 2013.北京地铁16号线对北京大学精密仪器实验楼振动影响预测分析报告[R].北京:北京大学.
② 北京大学环境振动监测与评估实验室. 2014.北京地铁16号线对北京大学精密仪器实验楼振动影响综合研究科研试验项目报告[R].北京:北京大学.
综上研究认为:(1)由于地铁或地面交通与地层的耦合作用,使得存在一个特定的频率, 当载荷以该频率输入时地面的振动最大, 当载荷频率小于或大于该频率的时候, 地面振动减小;(2)在地层不同位置激发振动,地表的最大反应频率不同;(3)本文采用的地层模型情况下,随地铁距离的增加,在5 Hz以下低频地面振动衰减缓慢, 8 Hz以上高频衰减快.本文采用二维模型没有考虑波在轨道方向传播,低估了空间土体的辐射特性,不能同时考虑径向和环向振动模态等问题,同时地层结构、隧道埋深、隧洞大小和埋深以及空腔的存在对地表的振动都有影响,这些问题还有待于进一步研究.以上这些结果对于如何在地铁沿线附近针对不同频率段的环境隔震减振需求来选择合理的工程措施或选线设计提供一种参考.
致谢 感谢审稿专家提出的修改意见和编辑部的大力支持!| [] | Bai B, Li X C. 2011. Application and Detection of FEPG Finite Element [M]. Beijing: Tsinghua University Press. |
| [] | Chatterjee P, Degrande G, Clouteau D, et al. 2003. Numerical modelling of ground borne vibrations from underground railway traffic[C].//6th National Congress on Theoretical and Applied Mechanics, KU Leuven. |
| [] | Committee of Environmental Geophysics of Chinese Geophysical Society. 1997. Environmental problems and environmental geophysics in China[J]. Acta Geophysica Sinica , 40(S1): 442–449. |
| [] | Degrande G, Clouteau D, Othman R, et al. 2006. A numerical model for ground-borne vibrations from underground railway traffic based on a periodic finite element-boundary element formulation[J]. Journal of Sound and Vibration, 293(3-5): 645–666. DOI:10.1016/j.jsv.2005.12.023 |
| [] | Ding D Y, Liu W N, Li K F, et al. 2011. Experimental study on the transmission characteristics of low-frequency vibrations induced by metro operation[J]. China Railway Science , 32(2): 20–26. |
| [] | Fujikake T. 1986. A prediction method for the propagation of ground vibration from railway trains[J]. Journal of Sound and Vibration, 111(2): 357–360. DOI:10.1016/S0022-460X(86)80168-7 |
| [] | Geng W L, Liu D Y, Cai Y E, et al. 2014. Prediction of the influence of the proposed Beijing metro line 16 on a precise instrument of Peking University[J]. Earthquake Engineering and Engineering Dynamics , 34(6): 19–25. |
| [] | Geng W L, Liu D Y, Zhang Q, et al. 2013. Simulate the subway vibration numerical method of the impact of precision instruments (in Chinese)[C].//Chinese Geophysics, Chinese Geophysical Society. |
| [] | Gupta S, Stanus Y, Lombaert G, et al. 2009. Influence of tunnel and soil parameters on vibrations from underground railways[J]. Journal of Sound and Vibration, 327(1-2): 70–91. DOI:10.1016/j.jsv.2009.05.029 |
| [] | Karlström A, Boström A. 2006. An analytical model for train-induced ground vibrations from railways[J]. Journal of Sound and Vibration, 292(1-2): 221–241. DOI:10.1016/j.jsv.2005.07.041 |
| [] | Lei J, Zhang Z Q, Zhang X B, et al. 2013. Subway vibration attenuation characteristic research of Beijing area (in Chinese)[C].//Chinese Geophysics, Chinese Geophysical Society. |
| [] | Lei J, Zhang Z Q, Zhao C H, et al. 2010. The environmental vibration comparative study of the east gate of Peking University before and after Beijing metro line 4 open to traffic (in Chinese)[C].//Chinese Geophysics, Seismological Society of China, 698. |
| [] | Li R D, Zhang H R, Liu W N. 2007. Testing and analysis of metro-induced ground vibrations response near Beijing metro line 1[J]. Journal of Beijing Jiaotong University , 31(4): 31–34. |
| [] | Liang G P. 2009. Finite Element Language [M]. Beijing: Science Press. |
| [] | Lou M L, Jia X P, Yu J Q. 2009. Field measurement and analysis of Ground Vibration Induced by subway trains[J]. Journal of Disaster Prevention and Mitigation Engineering , 29(3): 282–288. |
| [] | Meng X C, Jing L P, Sun H F. 2010. Ground vibration induced by metro running[J]. World Earthquake Engineering , 26(S): 310–314. |
| [] | Tao L J, Li X L, Lu X, et al. 2003. Study on attenuation law of ground motion induced by subway shock[J]. World Earthquake Engineering , 19(1): 83–87. |
| [] | Wang Y. 1992. Investigation and study on vibration effects of Beijing underground trains up or environments[J]. Metro and Light Rail , 16(2): 21–24, 33. |
| [] | Wolf S. 2003. Potential low frequency ground vibration (< 6.3 Hz) impacts from underground LRT operations[J]. Journal of Sound and Vibration, 267(3): 651–661. DOI:10.1016/S0022-460X(03)00730-2 |
| [] | Xia H, Wu X, Yu D M. 1999. Environmental vibration induced by urban rail transit system[J]. Journal of Northern Jiaotong University , 23(4): 1–7. |
| [] | Xie W P, Sun H G. 2003. FEM analysis on wave propagation in soils induced by high speed train loads[J]. Chinese Journal of Rock Mechanics and Engineering , 22(7): 1180–1184. |
| [] | Yang Y B, Hung H H. 2001. A 2.5D finite/infinite element approach for modelling visco-elastic bodies subjected to moving loads[J]. International Journal for Numerical Methods in Engineering, 51(11): 1317–1336. DOI:10.1002/nme.208 |
| [] | Yang Y B, Hung H H. 2009. Wave Propagation for Train-Induced Vibrations-A Finite/Infinite Element Approach[M]. Hackensack, NJ, Singapore: World Scientific. |
| [] | Yang Y B, Hung H H, Hsu L C. 2008. Ground vibrations due to underground trains considering soil-tunnel interaction[J]. Interaction and Multiscale Mechanics, 1(1): 157–175. DOI:10.12989/imm.2008.1.1.157 |
| [] | Zheng X, Tao X X, Wang F T, et al. 2013. An auto-cross PSD method to remove background vibration from observational records of traffic environment vibration[J]. Chinese Journal of Geophysics , 56(1): 348–353. DOI:10.6038/cjg20130136 |
| [] | 白冰, 李小春. 2011. FEPG有限元应用深入剖析[M]. 北京: 清华大学出版社. |
| [] | 丁德云, 刘维宁, 李克飞, 等. 2011. 地铁运营引起的环境低频振动传播特征试验研究[J]. 中国铁道科学, 32(2): 20–26. |
| [] | 耿万里, 刘敦宇, 蔡永恩, 等. 2014. 预测北京地铁16号线振动对北京大学精密仪器的影响[J]. 地震工程与工程振动, 34(6): 19–25. |
| [] | 耿万里, 刘敦宇, 张琼, 等. 2013. 模拟地铁振动对精密仪器影响的数值方法[C]. //中国地球物理2013——第二十四分会场论文集, 中国地球物理学会. |
| [] | 雷军, 张志强, 张献兵, 等. 2013. 北京地区地铁振动衰减特征研究[C]. //中国地球物理2013——第二十四分会场论文集, 中国地球物理学会. |
| [] | 雷军, 张志强, 赵长海, 等. 2010. 北京4号地铁线通车前后北京大学东门环境振动的比较研究[C]. //中国地球物理2010——中国地球物理学会第二十六届年会、中国地震学会第十三次学术大会论文集, 中国地震学会, 698. |
| [] | 栗润德, 张鸿儒, 刘维宁. 2007. 北京地铁1号线地面振动响应测试与分析[J]. 北京交通大学学报, 31(4): 31–34. |
| [] | 梁国平. 2009. 有限元语言[M]. 北京: 科学出版社. |
| [] | 楼梦麟, 贾旭鹏, 俞洁勤. 2009. 地铁运行引起的地面振动实测及传播规律分析[J]. 防灾减灾工程学报, 29(3): 282–288. |
| [] | 孟宪春, 景立平, 孙海峰. 2010. 地铁运行对地面环境的振动影响[J]. 世界地震工程, 26(S): 310–314. |
| [] | 陶连金, 李晓霖, 陆熙, 等. 2003. 地铁诱发地面运动的衰减规律的研究分析[J]. 世界地震工程, 19(1): 83–87. |
| [] | 王毅. 1992. 北京地下铁道振动对环境影响的调查与研究[J]. 地铁与轻轨, 16(2): 21–24, 33. |
| [] | 夏禾, 吴萱, 于大明. 1999. 城市轨道交通系统引起的环境振动问题[J]. 北方交通大学学报, 23(4): 1–7. |
| [] | 谢伟平, 孙洪刚. 2003. 地铁运行时引起的土的波动分析[J]. 岩石力学与工程学报, 22(7): 1180–1184. |
| [] | 张琼, 雷军, 刘敦宇, 等. 2013. 隧道空腔以及上方高低速夹层对地表振动的影响[C]. //中国地球物理2013——第二十四分会场论文集, 中国地球物理学会. |
| [] | 郑鑫, 陶夏新, 王福彤, 等. 2013. 去除交通环境振动观测记录中本底振动的自互功率谱法[J]. 地球物理学报, 56(1): 348–353. DOI:10.6038/cjg20130136 |
| [] | 中国地球物理学会环境地球物理专业委员会. 1997. 我国环境问题与环境地球物理学[J]. 地球物理学报, 40(S1): 442–449. |
 2017, Vol. 32
2017, Vol. 32


